´ ` t c ME c MD t = > =
Anuncio

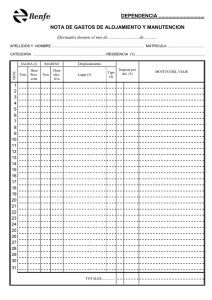
5. Relatividad de la simultaneidad. Como hemos visto la relatividad de Galileo está relacionada con el postulado de tiempo absoluto (t=t’) y la de Einstein con el postulado de constancia de la velocidad de la luz (c=c´). Ahora vamos a ver como el concepto de simultaneidad ( que dos sucesos ocurran al mismo tiempo) varía cuando se acepta uno u otro postulado. Volvamos a nuestro tren. Supongamos que el maquinista está situado al principio del tren (P) y un ayudante en el vagón de cola (C) y que desde un vagón en la mitad del tren (M) otro ayudante enciende una bombilla. Para el observador que enciende la bombilla la luz tardará un tiempo tA=MP/c en llegar al maquinista y un tiempo tB=MC/c para llegar al vagón de cola. Como MP=MC el tiempo que tardará en llegar la luz a la cabeza y a la cola del tren será el mismo (tA = tB) y el observador pensará que la recepción de la luz por el maquinista y su ayudante en la cola del tren será simultánea. ¿Qué le parecerá al jefe de estación que ve pasar al tren? Como vamos a ver la respuesta no es la misma en la relatividad de Galileo que en la de Einstein. (i) Relatividad de Galileo. En este caso el tiempo es absoluto y los tiempos medidos por el observador en el tren (tA, tB) han de ser los mismos que los medidos por el observador en la estación (t’A, t’B). Es decir: t’A = tA t’B = tB, y como tA = tB entonces tA’= tB’. Luego el jefe de estación y cualquier otro observador verán que la recepción de la luz es simultánea. Es decir, la simultaneidad es un concepto absoluto en la relatividad de Galileo. (ii) Relatividad de Einstein. Situémonos en el sistema del jefe de estación que ve pasar el tren. Cuando se enciende la luz en el medio del tren verá que el maquinista en la cabeza y el ayudante en la cola están a la misma distancia de la luz, MP’=MC’. Pero esta situación va cambiando ya que por efecto del movimiento del tren el maquinista parece huir de la luz que se aproxima a él mientras que el ayudante en la cola se va acercando. De hecho la luz tendrá que recorrer un camino mas largo para llegar al maquinista (MD’) que para llegar al ayudante en la cola (ME’), MD’>ME’ y como la velocidad de la luz es, según Einstein siempre la misma (c), tendremos que la luz llegará antes al ayudante situado en la cola que al maquinista: t D' = MD' ME´ ' > = tE c c Es decir, desde el punto de vista del jefe de estación, los dos observadores (el maquinista y su ayudante) no reciben al mismo tiempo la luz. Esto quiere decir que la simultaneidad es un concepto relativo en la teoría de Einstein. Merece la pena dedicar algún esfuerzo a analizar matemáticamente este experimento ya que tiene consecuencias muy sorprendentes. Para llegar al maquinista la luz tendrá que recorrer la distancia que hay hasta el maquinista cuando se enciende la bombilla (MP’) más la distancia que avanza el tren huyendo de la luz (P’D’) desde ese momento. Esta distancia será igual a la velocidad que lleva el tren (ux)multiplicada por el tiempo que tarda la luz en alcanzar al maquinista (tD’): P ' D' = u xt D' El tiempo que tarda en llegar la luz será la distancia total que recorre la luz (MP’+P’D’) dividida por la velocidad de la luz: t D' = MP' u xt D' + c c Despejando tD’ en esta ecuación obtenemos t D' = MP' c − ux ¿Que quiere decir este resultado? Que si ux es lo suficientemente parecido a c puede transcurrir un tiempo arbitrariamente grande hasta que la luz llegue al maquinista. Es decir, escogiendo arbitrariamente el sistema de referencia podemos hacer que un suceso se retrase tanto como queramos. Para llegar al ayudante del maquinista la luz tendrá que recorrer la distancia que hay hasta el maquinista cuando se enciende la bombilla (MC’) menos la distancia que avanza el tren al encuentro de la luz (C’F’) desde ese momento. Esta distancia será igual a la velocidad que lleva el tren (ux)multiplicada por el tiempo que tarda la luz en alcanzar al ayudante del maquinista (tE’): C ' F ' = u xt E' El tiempo que tarda en llegar la luz será igual a la distancia recorrida (MC’C’F’) dividida por la velocidad de la luz: t E' = MC ' u xt E' − c c Despejando tE’ en esta ecuación obtenemos t E' = MC ' c + ux En este caso podemos adelantar el suceso. Sin embargo nuestra capacidad para ‘adelantar’ un suceso no es ilimitada ya que ux puede valer como mucho c. Y el retraso con que llega la señal al maquinista respecto al ayudante será (según el jefe de estación): t D' − t E' = MP' MC ' − c − ux c + ux teniendo en cuenta que MP’=MC’ ya que la bombilla se enciende a la mitad del tren: ⎡ 1 1 ⎤ − t D' − t E' = MP' ⎢ ⎥ ⎣ c − ux c + ux ⎦ y operando esta expresión se reduce a: t D' − t E' = 2 MP' u x c c 1 −u x2 c 2 Es decir, si el tren está parado los dos observadores recibirían la luz al mismo tiempo, pero a medida que la velocidad del tren aumente, el retraso sería cada vez mayor. Esta pérdida del concepto de simultaneidad absoluta es típica de la relatividad de Einstein. De este experimento se deduce que cambiando la velocidad del sistema de referencia desde el que se hace una medida es posible jugar a placer con el concepto de simultaneidad ya que somos capaces de retrasar un suceso tanto como queramos. Un resultado sorprendente de la relatividad de Einstein es, por tanto, que siempre podemos encontrar un sistema de referencia en el que dos sucesos arbitrarios sean simultáneos, es decir, podríamos encontrar, por ejemplo, un observador para el que el descubrimiento de América por Colón y el primer alunizaje de Amstrong fueran sucesos simultáneos. ¿Es realmente cierto que podemos hacer que cualesquiera dos sucesos sean simultáneos o dejen de serlo escogiendo arbitrariamente el sistema de referencia? Consideremos los dos sucesos siguientes: (A) un coche atraviesa el punto medio de un paso de peatones y (B) un peatón se sitúa en el mismo punto. Esta claro que no podemos conseguir jugando solo con la elección del sistema de referencia que A y B sean simultáneos y que el peatón sea atropellado. Es decir si dos sucesos tienen lugar en un mismo punto y son simultáneos lo son para todos los observadores. Esta es la única limitación a la capacidad para jugar con la simultaneidad.