instituto tecnologico de chilpancingo algebra lineal

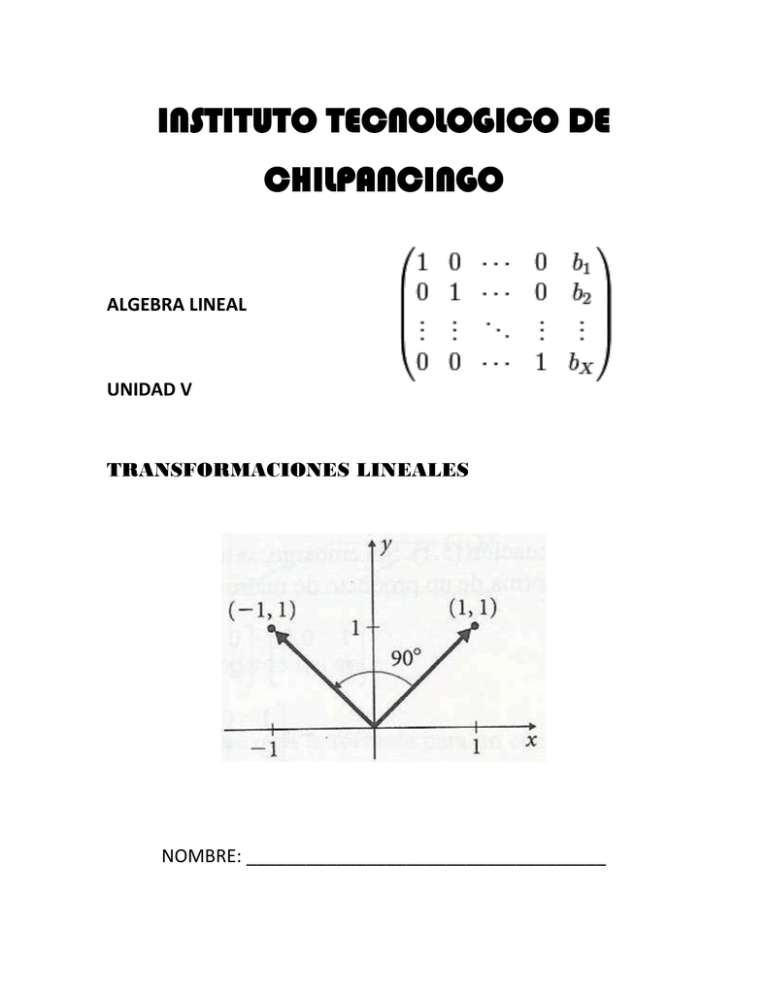
INSTITUTO TECNOLOGICO DE
CHILPANCINGO
ALGEBRA LINEAL
UNIDAD V
TRANSFORMACIONES LINEALES
NOMBRE: ____________________________________
Introducción
Las transformaciones lineales dentro del álgebra lineal no solo juegan un papel importante
por ser casos especiales de funciones definidas sobre espacios vectoriales si no porque
aparecen en diversas áreas de la matemática tanto a nivel teórico como aplicado. El
estudio de éste concepto aparece en el temario de los primeros cursos de álgebra lineal
de las carreras de ingeniería y de matemáticas en donde los alumnos se enfrentan con los
distintos lenguajes abstractos propios del álgebra lineal se aborda al álgebra lineal de
modo expositivo, el cual puede no dar el tiempo suficiente para que los alumnos
construyan sus conocimientos de forma adecuada.
Una transformación es un conjunto de operaciones que se realizan sobre un vector para
convertirlo en otro vector.
Los espacios vectoriales son conjuntos con una estructura adicional, al saber, sus
elementos se pueden sumar y multiplicar por escalares del campo dado, conviene utilizar
funciones que preserven dicha estructura. Estas funciones se llamaran transformaciones
lineales y en el presente capitulo las estudiaremos. Mas adelante mostraremos que las
transformaciones lineales se pueden representar en términos de matrices, y viceversa.
Se denomina transformación lineal a toda función cuyo dominio e imagen sean espacios
vectoriales y se cumplan las condiciones necesarias. Las transformaciones lineales
ocurren con mucha frecuencia en el álgebra lineal y en otras ramas de las matemáticas,
tienen una gran variedad de aplicaciones importantes. Las transformaciones lineales
tienen gran aplicación en la física, la ingeniería y en diversas ramas de la matemática.
Estudiaremos las propiedades de las transformaciones lineales, sus diferentes tipos, así
como la imagen, el núcleo, y como se desarrolla en las ecuaciones lineales.
Antecedentes
El lenguaje abstracto de las transformaciones lineales confronta a los alumnos con una
nueva manera de referirse a las propiedades de este tipo de funciones definidas sobre
espacios vectoriales. Así, este concepto les presenta situaciones que no van de acuerdo a
sus modelos que se han formado sobre las funciones univaluadas en los números reales
o complejos que han estudiado en sus cursos previos de cálculo, se puede decir que la
definición de una función en dos entradas o multivaluada es nueva para ellos. Así, para la
introducción del concepto de transformación lineal podría tomarse en cuenta el concepto
de función multivaluada.
2
El estudio de las transformaciones lineales desde diferentes puntos de vista.
El estudio de los conceptos del álgebra lineal presenta para los alumnos una serie de
dificultades puesto que, en la mayoría de las ocasiones, es el inicio de su primer curso
formal de matemáticas. Dorier y Sierpinska (2001) mencionan algunas de las razones por
las que algunos estudiantes encuentran difícil aprender el álgebra lineal.
La aproximación axiomática al álgebra lineal parece irrelevante para muchos estudiantes,
es decir, todos los problemas que se le plantean en su primer año de universidad las
pueden resolver sin usar la teoría de espacio vectorial, así esta teoría tiene una ligera
oportunidad de ser percibida por los estudiantes como una necesidad intelectual.
El álgebra lineal es un “explosivo compendio” de lenguajes y sistemas de representación.
Está el lenguaje geométrico de líneas y planos, el lenguaje algebraico de ecuaciones
lineales, n – tuplas y matrices, el lenguaje abstracto de espacio vectorial y
transformaciones lineales. Están los registros de lenguajes del álgebra lineal, el gráfico, el
tabular, el simbólico. Están también las representaciones cartesianas y paramétricas de
los subespacios. Los maestros y los libros de texto cambian constantemente entre estos
lenguajes, registros y modos de representación sin conducir al tiempo necesario para
hacer tales conversiones y discutir su validez.
El álgebra lineal es altamente demandante desde el punto de vista cognitivo. En el nivel
más general, el entendimiento del álgebra lineal requiere mucha flexibilidad cognitiva en la
transición entre los varios lenguajes (el lenguaje de la teoría de matrices y el lenguaje de
la teoría de espacio vectorial), puntos de vista (cartesianos y paramétricos) y registros
semióticos.
Los estudios tendientes a dar cuenta de las dificultades de los estudiantes se han
centrado en conceptos particulares del ágebra lineal, entre ellos podemos mencionar:
espacios vectoriales ( Dorier, 1995a, 1995b; Fischer, 2005; Maracci, 2005; Trigueros y
Oktaç, 2006; Vargas, 2006); bases ( Ku et al., 2008), sistemas de ecuaciones (Trigueros,
M., et al.; 2007), transformaciones lineales (Roa y Oktaç, 2010). Y, como podemos
observar, investigaciones que den cuenta de las dificultades que presentan los
estudiantes cuando se enfrentan al estudio de las transformaciones lineales, se encuentra
en sus inicios.
Por su parte Siñeriz y Santinelli (2005) presentan una propuesta metodológica sobre la
enseñanza de transformaciónes rígidas (isometrías) usando el cabrii geometre II como
programa auxiliar para la construción del concepto de transformación lineal en alumnos de
licenciatura, las actividades presentadas apuntan a la adquisición de un sólido
conocimiento disciplinar y a la puesta en juego de procesos matemáticos, a través de
situaciones que propician la retroalimentación entre las instancias inductivas y la
formalización matemática.
Uicab y Oktaç (2006) presentan resultados de investigación referente al problema de
extensión lineal presentado a unos alumnos. Ellas explican las dificultades encontradas
en los alumnos como la ausencia de conexiones entre el pensamiento teórico y el
3
pensamiento práctico propuesto por Sierpinska. Además agregan que las distintas
visiones que tienen los profesores y los estudiantes acerca del concepto de
transformación lineal influye en el aprendizaje de este concepto. Los profesores tiene una
visión sistemica del concepto mientras que los alumnos ven este concepto de forma
fraccionada.
Molina y Oktaç (2007) presentan una explicación de las dificultades de los alumnos sobre
el concepto de transformación lineal desde el punto de vista de Fischbein (1987) sobre la
intuición y los modelos intuitivos, enfocandose en identficar aquellos modelos intuitivos
que pudieran tener algunos estudiantes sobre el concepto de la transformación lineal en
contexto geométrico. Así encuentran que en los estudiantes pensaban a la la
transofrmación lineal en ejemplos prototipos o modelos.
Por otro lado (Roa y Oktaç, 2010) presentan el proceso de descomposición genética de
un concepto matemático desde el punto de vista de la teoría APOE (Asiala, Brown,
DeVries, Dubinsky, Mathews & Thomas, 1996). Ellas presentan el caso de la
transformación lineal, proponiendo dos posibles caminos para su construcción, el primero
basado en que el estudiante posee una concepción objeto de transformación lineal y
entonces se procede a la desencapsulación de dicho objeto y el segundo basado en el
esquema de función.
Los estudios anteriores muestran la diversidad de enfoques que se han utilizado para
tratar de dar un camino adecuado para que el alumno realice las construcciones mentales
adecuadas en relación a las transformaciones lineales, algunas de ellas presentan la
forma de como presentar este concepto a través de una secuencia o metodología basada
en un programa computacional, mientras que otras toman en cuenta los modelos intuitivos
construidos en diversos momentos por los estudiantes y cómo estos limitan su
aprendizaje. La construcción del esquema de este concepto y sus relaciones establecidas
con las de otros conceptos precisa de investigaciones profundas a fin de proponer nuevas
manera de abordar y enfrentar las dificultades mostradas por los alumnos.
4
DEFINICIÓN Y EJEMPLOS
Sean V y U dos espacios vectoriales. se dice que la función
T: V
U
Es una transformación lineal si
1) T preserva sumas
T(v1 +v2)=T(v1)+T(v2)
V v1,v2€V
2) T preserva producto por escalares
T(cv)= cT(v)
V v€V
Vc€R
En el caso particular en que V=U se dice que T es un operador lineal. Una transformación
lineal es, pues, una función entre dos espacios vectoriales “que preserva las operaciones
de espacio vectorial”, en el sentido de que: 1) la imagen de una suma de vectores en su
dominio es la suma de las imágenes de cada uno de los vectores, y 2) la imagen del
producto de un vector en su dominio por un escalar es el producto de la imagen del vector
por el escalar.
EJEMPLO 1:
El primer ejemplo que se verá (uno de los ejemplos triviales) es la transformación cero:
sea T: V
U la transformación tal que T(v) = 0V v €V. entonces T es una transformación
lineal pues:
T(v1+v2)=0=0+0=T(v1)+T(v2)
T(cv)=0=c(0)=cT(v)
y se denotara esa transformación por 0.
EJEMPLO 2:
Otro ejemplo (también trivial como el anterior) está dado por la transformación identidad
T:V
V definida por T(v)=v V v € V (observese que T es un operador lineal). T es una
transformación lineal, pues:
T(v1+v2)=v1+v2=T(v1)+T(v2)
T(cv)=cv=cT(v)
Se denotará esta transformación por Id ( o mas explícitamente con Idv).
5
EJEMPLO 3:
Véase un ejemplo geométrico. considerese de transformación T=R²
R² definida de la
siguiente manera: para v=(x,y) € R², T(v) es el vector de R² que geométricamente
representa la reflexión del vector v respecto del eje x.
y
y
v
v
x
x
T(v)
Al ver la siguiente figura uno se puede convencer de que T preserva sumas:
y
y
v1+v2
v2
v1
x
T(v1)
T(v2)
6