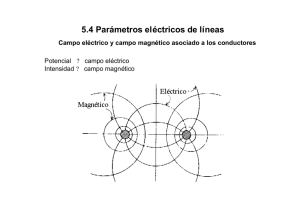
05 UNIDAD_LINEAS DE TRANSMISION
Anuncio

Tecsup Unidad 5 : Líneas de Transmisión Tecsup Virtu@l Índice Índice 1. INTRODUCCIÓN........................................................................................................ 1 1.1. PARÁMETROS DE LAS LÍNEAS DE TRANSMISIÓN ............................................... 3 1.1.1. RESISTENCIA ELÉCTRICA ...................................................................... 3 1.2. INDUCTANCIA Y CAPACITANCIA DE LÍNEAS DE TRANSMISIÓN .......................... 8 1.3. LA INDUCTANCIA ............................................................................................. 8 1.4. FLUJO CONCATENADO Y LEY DE FARADAY ........................................................ 9 1.5. LA CAPACITANCIA...........................................................................................10 1.6. FLUJO DE CAMPO ELÉCTRICO Y LEY DE GAUSS ................................................10 1.7. CÁLCULO DE LA REACTANCIA INDUCTIVA........................................................11 1.8. CÁLCULO DE LA CAPACITANCIA DE UNA LÍNEA TRIFÁSICA ...............................12 1.9. REPRESENTACIÓN DE LAS LÍNEAS ...................................................................12 1.9.1. REDES DE CUATRO TERMINALES ..........................................................12 1.9.2. LÍNEA CORTA (Hasta 80 Km) ................................................................15 1.9.3. LÍNEA MEDIA (hasta 240 Km) ...............................................................17 1.9.4. LÍNEA LARGA (Superior a 240 Km) ........................................................18 1.9.5. EJEMPLOS ............................................................................................20 1.9.6. MÁXIMA POTENCIA DE CARGA PARA LÍNEAS DE TRANSMISIÓN .............23 1.9.7. COMPENSACIÓN REACTIVA EN LÍNEAS DE TRANSMISIÓN ......................26 Tecsup Virtu@l Sistemas Eléctricos de Potencia UNIDAD 5 “LÍNEAS DE TRANSMISIÓN” 1. INTRODUCCIÓN Una línea eléctrica es un conjunto de conductores, aislantes y elementos accesorios destinados a la transmisión de la energía eléctrica. Los conductores son, en general, de aluminio, cobre, aldrey. TIPOS : Las líneas se clasifican siguiendo diferentes criterios: • • • • Situación en el espacio: Líneas aéreas, líneas subterráneas (cables) Clase de tensión: Líneas de Baja Tensión (menores a 1 kV) y líneas de Alta Tensión (mayores a 1 kV). Naturaleza de la tensión continua, alterna monofásica o trifásica. Longitud: Línea corta, media o larga. La línea de transmisión de potencia trifásica aérea constituye el medio de transporte principal de la energía eléctrica en un sistema de potencia. La línea de transmisión produce tres efectos, que por su orden de importancia la podemos mencionar como: • • • El campo magnético producido por la corriente eléctrica, provoca caídas de tensión en la línea. El efecto capacitivo, resultante de los campos eléctricos entre conductores y conductores de tierra. La resistencia óhmica de los conductores, considerando el material del cable de energía. Un cuarto efecto podría ser el provocado por las corrientes de fuga, que fluye a través de las películas contaminadas de los aisladores. Los cables de guarda están eléctricamente en contacto con la torre y, por tanto, a tierra; sirven principalmente como defensa contra rayos. Los conductores de fase son mucho más grandes que los cables de guarda, comúnmente de aluminio cableado con alma de acero, para aumentar su resistencia a la tracción. Algunas veces por cada fase se incluyen más de un conductor. Los cables son desnudos para tener mejor disipación del calor; los conductores de fase están aislados entre sí y la torre mediante una cadena de aisladores. RAZONES PARA CONSTRUIR UNA LÍNEA: • • Crecimiento de la carga, llevando a que las líneas existentes operen cerca de sus límites de estabilidad y capacidad térmica. Esto podría demostrarse, si los niveles de confiabilidad del sistema han caído debajo de los niveles aceptables. Por tanto la inclusión de líneas podrá mejorar las características de estabilidad en régimen transitorio de los generadores. El incremento de líneas permitirá una mayor flexibilidad en la operación del sistema. -1- Tecsup Virtu@l Sistemas Eléctricos de Potencia La capacidad de transporte de la línea está relacionada con su longitud y con la tensión de la misma. Para una longitud dada, la capacidad de transporte varía con el cuadrado de la tensión, mientras que el costo de la línea, varía en forma lineal con la tensión. Fig 5.1 Potencia transmitida en función de la longitud y de la tensión de transmisión Eso quiere decir que cuanto mayor sea la capacidad de transporte o mayor la longitud de la línea, mayor deberá ser la tensión de transmisión. Para la elección de la tensión, se elige valores normalizados, por la disponibilidad del equipamiento. Supóngase que se eligen regímenes nominales de potencia y tensión para una línea determinada de longitud conocida, también se deberá analizar el número, diámetro y espaciamiento de los conductores por fase, para ello se deberá evaluar el efecto corona e impedancia de la línea. Asimismo, se debe de escoger la distancia entre fases, el número, ubicación y tipo de conductor para los cables de guarda; que es la protección contra descargas atmosféricas. Se debe de elegir el nivel de aislamiento, y la cantidad de aisladores que se deberán utilizar en la cadena. Cuando el peso de la línea sea esencialmente constante, la atención se debe dirigir al diseño de la torre. Se considerarán las condiciones climatológicas del lugar, específicamente, se estimarán razonablemente las peores condiciones de vientos y nieves, ya que están relacionados con la carga que soporta la torre. -2- Tecsup Virtu@l Sistemas Eléctricos de Potencia 1.1. PARÁMETROS DE LAS LÍNEAS DE TRANSMISIÓN 1.1.1. RESISTENCIA ELÉCTRICA Los cables de las líneas de transmisión dependen de sus características. En DC la resistencia que presente es: Donde: • • • ρ = Resistividad del conductor L = Longitud del conductor A = Sección del conductor Pero los conductores de las líneas aéreas normalmente son cableados con alma de acero, para tener mayor carga de rotura. Los cables pueden ser de aluminio o cobre, aunque el más usado es el aluminio por su menor peso. Los conductores de aluminio se designan como: • • • • AAC AAAC ACSR ACAR Conductor Conductor Conductor Conductor totalmente de aluminio totalmente de aleación de aluminio de aluminio con alma de acero de aleación de aluminio con alma de acero La sección de los conductores frecuentemente se da en términos de “circular mils”. Un circular mil.- es el área de un círculo que tiene como diámetro una milésima de pulgada (0,001 pulg). Un MCM.- es igual a 1000 circular mils. Un conductor de aluminio cableado de 1000 MCM tiene un diámetro de una pulgada. La resistencia a las frecuencias nominales, bien sea como cable o como conductor sólido, es mayor que la resistencia en DC debido al efecto pelicular (SKIN). RAC > RDC El efecto skin (pelicular o superficial) es la tendencia que tiene la corriente alterna a concentrarse en la superficie del conductor, producto del efecto de oposición al flujo de corriente al centro del conductor. Mientras que en corriente continua, ésta se distribuye uniformemente en el conductor. Cabe indicar que el efecto SKIN se incrementa con la sección del conductor, por su permeabilidad magnética y con la frecuencia. Es por ello, que estos son algunas de las razones del porqué los conductores de las L.T. son cableados. -3- Tecsup Virtu@l Sistemas Eléctricos de Potencia También hay que considerar el cambio de la resistencia debido a la variación de temperatura del conductor (influencia del coeficiente de temperatura sobre la resistencia). La resistividad (ρ) varía con la temperatura según la relación: Donde : To = 228 para el aluminio ρ1 , ρ2 = Resistividades a las temperaturas T1 y T2 en °C. También se tiene la siguiente relación: Donde: Por lo general, esta expresión se aplica a las resistencias: R2 = R1 * [1 + α (T2 - T1) ] CÁLCULO DE LA RESISTENCIA Para el cálculo de las resistencias, muchas veces no es necesario aplicar las relaciones anteriores, porque los fabricantes dan las tablas de las características eléctricas de los conductores. Las tablas 5.1 y 5.2 son un ejemplo de algunos datos disponibles. Ejemplo : La resistencia por fase de 200 Km. De una línea de transmisión de 636 MCM , ACSER es : R Ω = r . L = (0,101) x 200 Km = 20,2 Ω 50° C Km Donde: r = L = Resistencia por unidad de longitud y por fase. (Ω/Km-fase) Longitud de la línea en Km. -4- Tecsup Virtu@l Sistemas Eléctricos de Potencia TABLA 5.1 CARACTERÍSTICAS PRINCIPALES DE CABLES DE ALUMINIO Calibre Conductor Diámetro Exterior Peso AWG MCM mm Kg/Km 6 4.7 37 4 5.9 2 Número de Hilos Resistencia a 50° C Tensión de Ruptura Radio Medio Geométrico Kg m 7 240 0.00169 2.432 2.432 58 7 375 0.00213 1.529 1.529 7.4 93 7 575 0.00269 0.962 0.962 1 8.3 117 7 700 0.00302 0.762 0.762 1/0 9.3 148 7 845 0.00339 0.604 0.605 2/0 10.5 186 7 1065 0.00381 0.479 0.480 3/0 11.7 235 7 1290 0.00428 0.380 0.381 4/0 13.3 299 7 1630 0.00481 0.301 0.302 266.8 15.1 369 19 2180 0.00570 0.239 .0240 336.4 17.9 467 19 2780 0.00640 0.189 0.190 397.5 18.4 554 19 3120 0.00696 0.160 0.161 477 19.8 664 19 3670 0.00763 0.133 0.135 556.5 21.7 774 19 4280 0.00823 0.114 0.116 636 23.2 888 37 5100 0.00895 0.100 0.101 D.C. -5- 60 Hz. Ohms/conductor/Km. Tecsup Virtu@l Sistemas Eléctricos de Potencia TABLA 5.2 CARACTERÍSTICAS PRINCIPALES DE CABLES DE ALUMINIO REFORZADOS POR ACERO (ACSR) Calibre Conduct or AWG MCM 8 6 5 4 3 2 1 1/0 2/0 3/0 4/0 266.8 300 336.4 336.4 397.5 397.5 477 477 556.5 556.5 636 636 715.5 715.5 795 795 795 874.5 900 954 1033.5 1113 1192.5 1272 1351.5 1431 1510.5 1590 Diámetr o exterior MM Nombre Comercial 4.0 5.0 5.7 6.4 7.1 8.0 9.0 10.1 11.4 12.8 14.3 16.3 17.3 18.3 18.8 19.9 20.5 21.8 22.4 23.6 24.2 25.2 25.9 26.7 26.3 28.1 29.0 27.8 29.1 29.5 30.4 31.7 32.8 34.0 35.1 36.2 37.2 38.3 39.2 Reyezuelo Pavo Tordo Cisne Golondrina Gorrión Petirrojo Cuervo Codorniz Pichón Pingüino Perdiz Avestruz Jilgero Oriol Ibis Calandria Halcón Gallina Palomo Aguila Cardenal Airón Estornino Corneja Eider Anade Cóndor Grulla Canario Rojillo Zarapito Pinzón Grajo Faisán Vencejo Frailecillo Perico Falcón Peso Número hilos Kg/Km Al / Acero 6/1 6/1 6/1 6/1 6/1 6/1 6/1 6/1 6/1 6/1 6/1 26/7 26/7 26/7 30/7 26/7 30/7 26/7 30/7 26/7 30/7 26/7 30/19 26/7 54/7 26/7 30/19 54/7 54/7 54/7 54/7 54/7 54/19 54/19 54/19 54/19 54/19 54/19 54/19 35 55 70 85 110 140 170 220 270 340 430 550 610 690 790 810 930 980 1110 1140 1300 1300 1470 1470 1370 1630 1840 1520 1680 1720 1830 1920 2130 2280 2430 2590 2740 2890 3040 -6- Tensión de ruptura Kg 340 530 660 830 1020 1270 1580 1940 2420 3030 3820 5100 5740 6370 7730 7340 9060 8810 10570 10160 12340 11340 14300 12750 11930 14150 17420 12930 14240 14680 14700 16830 18230 19550 20320 21590 22860 24130 25400 Resistencia 50°C DC 60 Hz Radio medio geométrico Ohms/conductor/ Km 3.842 3.842 2.434 2.474 1.926 1.975 1.535 1.597 1.210 1.286 0.964 1.050 0.764 0.856 0.604 0.696 0.479 0.557 0.381 0.449 0.302 0.367 0.239 0.239 0.213 0.213 0.190 0.190 0.190 0.190 0.161 0.161 0.161 0.161 0.134 0.134 0.134 0.134 0.115 0.115 0.116 0.116 0.101 0.101 0.101 0.101 0.0896 0.896 0.0896 0.0921 0.0800 0.0800 0.0800 0.0800 0.0856 0.0856 0.0763 0.0763 0.0730 0.0730 0.0701 0.0701 0.0643 0.0643 0.0602 0.0602 0.0563 0.0563 0.0530 0.0530 0.0500 0.0500 0.0472 0.0472 0.0448 0.0448 0.0448 0.0428 cm. ---0.120 0.127 0.133 0.131 0.127 0.127 0.136 0.155 0.183 0.248 0.661 0.701 0.744 0.777 0.808 0.847 0.884 0.927 0.954 1.000 1.020 1.070 1.080 1.060 1.140 1.200 1.120 1.180 1.210 1.230 1.280 1.330 1.370 1.420 1.460 1.500 1.550 1.580 Tecsup Virtu@l Sistemas Eléctricos de Potencia Fig 5.2 Características de cables de aluminio reforzado TABLA 5.3 USO RECOMENDADO Se utilizan en líneas aéreas de distribución, transmisión y subestaciones, de acuerdo a la tabla siguiente: Calibre B.T. 2 1/0 3/0 266.8 336.4 477.0 795.0 900.0 1113.0 X X 6 KV 132 KV 23 KV 34.5 KV X X X X X X X X X X X X X X X X -7- 69 KV 85 KV X X X X X X X 115 KV X X X X 230 KV 400 KV X X X X X Tecsup Virtu@l Sistemas Eléctricos de Potencia 1.2. INDUCTANCIA Y CAPACITANCIA DE LÍNEAS DE TRANSMISIÓN En esta unidad estudiaremos los parámetros básicos utilizados en el modelamiento de líneas de transmisión de corriente alterna. Por modelo entiéndase una representación a través de circuitos equivalente y/o ecuaciones matemáticas. El tipo de modelo utilizado depende del tipo de estudio o proyecto que se pretende realizar. A pesar de algunas ideas discutidas en esta unidad tienen aplicación más general, estaremos interesados principalmente en modelos utilizados en estudios de transmisión de potencia eléctrica en situaciones de estado estable. Es decir, operación del sistema eléctrico con tensiones y corrientes variando senoidalmente (por ejemplo, con frecuencia de 60 Hz.). Consideremos además los sistemas operando en situaciones equilibradas. O sea, situaciones en las cuales una de las fases puede ser tomada como representativa de lo que ocurre en las demás. 1.3. LA INDUCTANCIA Físicamente, las líneas de transmisión nada más son conjuntos de conductores (de cobre o de aluminio) que transportan energía eléctrica de los generadores a las cargas. De la misma forma que existen carreteras más largas y otras más estrechas, y que ofrecen mayor o menor “resistencia” al flujo de vehículos, existen líneas que transportan potencia eléctrica con mayor o menor facilidad. Uno de los parámetros más importantes en definir la capacidad de transmisión de una línea de transmisión es la impedancia de la línea, que a su vez depende básicamente de la inductancia (más allá de la resistencia óhmica). Sabemos que una corriente eléctrica produce un campo magnético y un flujo magnético al asociado. La intensidad del flujo magnético varía directamente con la magnitud de la corriente; depende también de su distribución espacial (geometría del conductor) y del medio en el cual el conductor está insertado. La relación general entre flujo y corriente es dada por la Ley de Faraday, que es una de las ecuaciones de Maxwell. En particular, veremos que la inductancia de las líneas de transmisión en corriente alterna depende del tamaño de la línea: cuanto más larga es la línea, mayores son las inductancias y por tanto, mayores las impedancias y la oposición ofrecida por la línea para transmitir la potencia eléctrica. Esta es una de las razones por las cuales, para distancias más largas (por ejemplo, encima de los 1000 Km) líneas de transmisión en corriente continua se tornan económicamente más competitivas. -8- Tecsup Virtu@l Sistemas Eléctricos de Potencia El tamaño exacto a partir del cual las líneas de corriente continua pasan a predominar depende de muchos factores, incluyendo las tecnologías utilizadas en conversores AC/DC cuyos costos han variado con el tiempo. (fig. 5.3). Fig 5.3 Comparación de costos entre Transmisión trifásica en A.T. y Transmisión DC en A.T. A pesar de esa imprecisión, entre tanto, es seguro decir que las líneas de corriente alterna convencionales pierden competitividad en relación a la transmisión en corriente continua cuando las distancias involucradas aumentan. Este comportamiento está ligado a un parámetro fundamental que será estudiado a continuación: La inductancia de las líneas. 1.4. FLUJO CONCATENADO Y LEY DE FARADAY La Ley de Faraday establece que la tensión inducida en una espira conductora en un instante t; está dada por la razón entre la variación del flujo concentrado por una espira en aquel instante, o sea: Donde : e φC = = tensión inducida flujo concatenado (Weber-espiras). -9- Tecsup Virtu@l Sistemas Eléctricos de Potencia 1.5. LA CAPACITANCIA Ya fue dicho que las líneas de transmisión nada más son conjuntos de conductores de (cobre o aluminio) utilizados para transportar potencia eléctrica. Ya vimos también que a esos conductores está asociada una inductancia que influye principalmente en la capacidad de transmisión de potencia activa a través de la línea. De la misma forma, esos conductores presentan también una capacitancia que tiene efectos directos sobre el comportamiento reactivo (magnitudes de las tensiones) de la línea. Una corriente alterna que circula por una línea, produce un almacenamiento de cargas positivas y negativas en los conductores. A esta distribución de cargas a su vez están asociados campos eléctricos y potenciales eléctricos. La relación entre los flujos magnéticos concatenados y las corrientes correspondientes definen la inductancia de la línea; análogamente, la relación entre la diferencia de potencial y las densidades de carga correspondientes definen la capacitancia de las líneas. La relación entre cargas y flujos de campo eléctrico es regida por la Ley de Gauss, que es una de las ecuaciones de Maxwell. 1.6. FLUJO DE CAMPO ELÉCTRICO Y LEY DE GAUSS La Ley de Gauss para campos eléctricos establece que el flujo total a través de una superficie cerrada “s” es igual al total de la carga eléctrica existente en el interior de la superficie. Note que el campo eléctrico no es necesariamente debido solamente a las cargas internas; o que la Ley dice simplemente que el valor del flujo es igual al total de cargas internas a la superficie. Siendo D la densidad de campo eléctrico, ds un vector normal a la superficie, ρ densidad volumétrica de carga (o superficial, si la carga estuviera concentrada en la superficie), dv el elemento diferencial de volumen y q la carga total en el interior de s. - 10 - Tecsup Virtu@l Sistemas Eléctricos de Potencia 1.7. CÁLCULO DE LA REACTANCIA INDUCTIVA La reactancia inductiva unitaria (Ω / Km) de una fase de la línea de corriente trifásica con conductores de metal no ferroso, que tiene transposición de conductores, puede ser calculada por medio de la fórmula : Donde : f DMG RMG= = frecuencia de la red (Hz.) = Distancia media geométrica entre los conductores de la línea. Radio medio geométrico La distancia media geométrica entre los conductores de una línea simple es: DMG = 3 D12 D13 D 23 Cuando los conductores se disponen por los vértices de un triángulo equilátero de lado D. DMG = D Fig 5.4 Conductores dispuestos en triángulo equilátero Para la disposición horizontal DMG = 1,26 D Fig 5.5 Conductores dispuestos en un plano horizontal - 11 - Tecsup Virtu@l Sistemas Eléctricos de Potencia 1.8. CÁLCULO DE LA CAPACITANCIA DE UNA LÍNEA TRIFÁSICA La capacitancia entre conductores se determina por la relación siguiente: 1.9. REPRESENTACIÓN DE LAS LÍNEAS 1.9.1. REDES DE CUATRO TERMINALES Un circuito de constantes concentradas, pasivo lineal y bilateral, puede representarse por una red de 4 terminales. Por ejemplo, una línea de transmisión y un transformador. Fig 5.6 Cuadrípolo Los parámetros complejos A, B, C y D describen Red en función de las tensiones y corriente en los extremos de envío y de recepción del modo siguiente: VS = A VR + B IR IS = C VR + D IR Se cumple que: A D − B C = 1 Mediante mediciones y ciertas interpretaciones de tipo físico, pueden obtenerse A , B, C y D, del modo siguiente: - 12 - Tecsup Virtu@l Sistemas Eléctricos de Potencia 1.9.1.1. EXTREMO RECEPTOR CORTOCIRCUITADO Además, Impedancia de transferencia de cortocircuito. 1.9.1.2. EXTREMO RECEPTOR A CIRCUITO ABIERTO Con frecuencia es interesante tener una RED SIMPLE de 4 terminales para 2 ó más elementos de la Red en serio o paralelo. Por ejm: Fig 5.7 Red de cuatro terminales para 3 elementos de una red - 13 - Tecsup Virtu@l Sistemas Eléctricos de Potencia Redes Combinadas en Serie Fig 5.8 Red de cuadrípolos en serie Redes Combinadas en Paralelo Fig 5.10 Cuadrípolo equivalente Una línea de transmisión tiene como parámetros básicos su resistencia, inductancia, capacitancia y conductancia de dispersión uniformemente distribuida a lo largo de su longitud; y se pueden calcular por fase y por unidad de longitud, a partir de los parámetros dimensionales de la línea. En los casos prácticos, la conductancia de dispersión a tierra despreciable, por ser muy pequeña. En la operación en estado permanente, por lo general se tiene interés en las relaciones entre los voltajes y corrientes, al principio y al final de la línea. Para estos estudios en forma tradicional, se ha dividido el estudio de las líneas en tres categorías conocidas como línea corta, línea media, y línea larga; las ecuaciones de comportamiento en cada caso, se indican a continuación. - 14 - Tecsup Virtu@l 1.9.2. Sistemas Eléctricos de Potencia LÍNEA CORTA (HASTA 80 KM) A continuación se muestra el circuito equivalente de una línea corta; donde IS y VS representan los valores al principio de la línea (corriente y voltaje), y VR , IR voltaje y corriente al final de la línea (extremo de recepción). Fig.11 Circuito equivalente de una línea corta Las características relativas a este circuito, que se trata como un circuito serie en C.A., son las siguientes: IS = IR Z= R + j XL VS = VR + IR . Z Donde: Z = Es la impedancia total de la línea (Ω) Es decir, Z = z . L z = Impedancia por unidad de longitud. (Ω/km) L = Longitud de la línea. (km) El efecto de la variación del factor de potencia de la carga, sobre la regulación de voltaje, se observa en los siguientes diagramas vectoriales: - 15 - Tecsup Virtu@l Sistemas Eléctricos de Potencia Fig 5.12 Diagramas fasoriales para diferentes tipos de cargas. Se desprecian las capacidades Resistencias de pérdidas A =1 B= Z C=0 D=1 URO URPC Ureg% U RO − U R P .C . Ureg% = UR P .C . tensión recibida en vacío tensión recibida a plena carga porcentaje de regulación de tensión - 16 - x 100 Tecsup Virtu@l 1.9.3. Sistemas Eléctricos de Potencia LÍNEA MEDIA (HASTA 240 KM) La admitancia en derivación es generalmente capacitancia pura; y se incluye en los cálculos para líneas de longitud media, si el valor total de la admitancia se divide en dos partes iguales, y se localizan en ambos extremos; es decir, una mitad en el extremo de envío, y la otra en el extremo receptor. El circuito se conoce como circuito “TT” nominal. También se puede emplear la representación “T” equivalente. De estas dos versiones la representación a)Caso de la Red π De donde se obtienen En función de V R e IR V C = VR + Z IR 2 - 17 - π quizás les dé uso más general. Tecsup Virtu@l Sistemas Eléctricos de Potencia b)Caso de la Red en T 1.9.4. LÍNEA LARGA (SUPERIOR A 240 KM) Aquí el estudio supone que los parámetros están repartidos. Las variaciones de tensión y de corriente en una longitud elemental ∆x de la línea, situada a “x” metros del extremo de envío, están determinadas y las condiciones correspondientes a la línea completa se obtienen por interrogación: Sea: La tensión y corriente a “x” metros del extremo de envío. Donde : - 18 - Tecsup Virtu@l Sistemas Eléctricos de Potencia Cuando x = L ó Los parámetros de la red equivalente de 4 terminales son: A = D = cos h Z Y B= Z sen h Y ZY C= Y sen h Z ZY Para las líneas < 500 Km. ZY 2 ZY B = Z= 1+ 6 A = D= 1+ C = Y = 1+ - 19 - ZY 6 Tecsup Virtu@l Sistemas Eléctricos de Potencia Fig 5.14 Circuito equivalente de L.T. de longitud menor a 500 Km 1.9.5. EJEMPLOS EJEMPLO 1 Calcular la impedancia serie de una línea de transmisión de 230 kV, 300 Km. de longitud que usa un conductor por fase de 900 MCM tipo canario; que tiene de acuerdo a tablas, las características siguientes: DIÁMETRO EXTERNO : 29.5 mm., ACSR 54 / 7 RESISTENCIA ELÉCTRICA A 60 HZ. Y 50°C, 0.073 ohms / Km. El radio medio magnético es : 1,210 cm. La disposición de los conductores se muestra en la figura siguiente: 7m 7m 21m Fig.5.15 Disposición de conductores - 20 - Tecsup Virtu@l Sistemas Eléctricos de Potencia SOLUCIÓN La resistencia eléctrica a la temperatura de 50°C, es: R = r x L = 0.073 x 300 = 21.9 ohms. La reactancia inductiva se puede determinar de la expresión simplificada: XL = 0.1736 Log Donde : DMG = 3 Dab Dbc Dca = Con el dato de RMG = 1.21 cm. X L = 0.1736 Log Para 3 DMG RMG 7 x 7 x 14 DMG = 8.82 m. 882 = 0.497 ohms / Km 1.21 L = 300 Km. XL = 0.497 x 300 = 149 ohms EL CIRCUITO DE LA LÍNEA ES: 0,073Ω / km 0,497Ω / km 21,9Ω Fig. 5.16 (a) en por unidad de longitud j149Ω (b) para la longitud total LA ADMITANCIA EN DERIVACIÓN ES: Yc = R Yc 2 9.085 x 10 −6 9.085 x 10 −6 = = 3.173 x 10 −6 SIEMENS / KM / FASE DMG 882 Log Log RMG 1,21 j XL 0,073 Yc 2 0,497 1,585 × 10 −6 1,585 × 10 −6 Fig. 5.17 El circuito π de la línea, trabajando en por unidad. - 21 - Tecsup Virtu@l Sistemas Eléctricos de Potencia EJEMPLO 2 Calcular la reactancia inductiva y la susceptancia para una línea de transmisión de 400 kV, con 400 Km. de longitud, que tiene 2 conductores / fase de 1113 MCM, separados 45 cms., entre sí. El conductor es bluejay 1113 MCM, con diámetro de 3,25 cm. (54 / 19). La disposición de los conductores en la estructura, se muestra a continuación: 0,45 m 0,45 m 0,45 m 10 m 10 m SOLUCIÓN De acuerdo a la configuración de los conductores, la distancia media geométrica es: DMG = 3 10 x 10 x 10 = 12.6 m. Para más de un conductor por fase, el RMG se calcula como: R MG = Re q = n Donde: nr x R R n = número de conductores por fase n = 2 d = separación entre conductores por fase. d R= n sen π n = 45 = 22.5 cm. 180 2 sen 2 POR LO TANTO: R MG = - 22 - 2 2 x 1.625 x 22.5 = 8.55 cm. 22.5 Tecsup Virtu@l Sistemas Eléctricos de Potencia LA REACTANCIA INDUCTIVA ES POR LO TANTO: XL = 0.1736 Log DMG 1260 = 0.1736 Log RMG 8.55 Para la longitud total X L = 0,376 Ω Km fase X LT = 400 x 0.376 = 160.5 Ω / fase LA SUSCEPTANCIA: 9.085 x 10 6 9.085 X 10 6 Yc = = = 4.19 x 10 DMG 1260 Log Log RMG 8.55 6 (SIEMENS / KM.) PARA LA LONGITUD TOTAL: YCT = 400 X 4.19 X 10−6 = 1.67 x 10 −3 (SIEMENS / FASE ) 1.9.6. MÁXIMA POTENCIA DE CARGA PARA LÍNEAS DE TRANSMISIÓN Es de fundamental importancia considerar la pregunta: ¿Cuánta potencia es capaz de transmitir una línea de transmisión?. Hay dos límites básicos: primero, el límite térmico de la línea, sujeto a la capacidad de corriente portadora de los conductores de fase; segundo, el límite de estabilidad del estado estacionario, que es impuesto por los valores de impedancia de la línea. Se supone que la línea opera en su modalidad normal de estado estacionario senoidal trifásico balanceado, y en régimen nominal de voltaje. Solamente se requiere el circuito equivalente de secuencia límite térmico es: S3φnominal = VLnominal ILnominal positiva. El 3 Donde las unidades son el sistema SI (no en el sistema unitario). Existen ciertas dificultades para decidir cuál será la corriente de línea de régimen. Como el problema es el sobrecalentamiento del conductor son importantes la temperatura ambiental y la velocidad del viento. El problema no es insignificante cuando se considera que cada ampere, a 500 kV, representa 866 kVA de potencia transmitida. Evidentemente, el régimen nominal de los conductores en invierno deberá exceder al régimen de verano. - 23 - Tecsup Virtu@l Sistemas Eléctricos de Potencia Se deben interpretar los voltajes como línea a neutro, las corrientes como valores de línea y las impedancias como conectadas en estrella. Las unidades son SI. Las ecuaciones en parámetros A, B, C y D son: Vs = AVR + BIR I s = CVR + DI R Donde: A = A∠α = B = B∠β = Z c 1 B Z c2 C = D=A V s = V s ∠δ VR = VR ∠0 De la ecuación (4-78a): IR = Vs AVR − B B ΙR = VS AV R ∠δ − β − ∠α − β B B y Ι∗R = VS AV R ∠β − δ − ∠β − α B B La potencia compleja en el extremo receptor S es: S 3 φ R = 3V R Ι *R S 3φ R = 3V S V R ∠β − δ B − 3 AV B 2 R ∠β − α ....... → (θ ) Siendo constante Vs y Ve la única variable en la ecuación última es el ángulo de potencia δ. Representaremos gráficamente la ecuación, como en la figura 5.18 el lugar geométrico de SR en el plano PR, QR cuando δ varía, es una circunferencia. - 24 - Tecsup Virtu@l Sistemas Eléctricos de Potencia Cuando la potencia en el extremo receptor es cero, δ es pequeño (punto a). Aumenta δ a medida que se ve cargando la línea (punto b). Se puede seguir cargando la línea hasta el límite de la estabilidad en estado estacionario P3φss, si lo que se recomienda es un margen mínimo de aproximadamente 20% (es decir, P3φr ≤ 0.8 P3φss). De la ecuación; Ρ3φss = 2 VLnominal [1 − A cos( β − α )] B A medida que aumenta la longitud de una línea, este límite viene a ser el factor decisivo. El valor correspondiente de la potencia reactiva es: AV 2 Q 3φss = − Lnominal sen(β − α ) B y la correspondiente potencia aparente es: S 3φss = P 2 + Q2 3φss 3φss V2 S 3φss = Lnominal 1 + A 2 − 2A cos(β − α) B Este límite es decisivo cuando S3φss < S3φregimen. Estas ideas se desarrollan en un ejemplo de línea, en el apéndice. Fig. 5.18 Diagrama circular extremo receptor. QR d a QMAX o P3 φ β −α SS b δ 3 AV r B 3V sV r pc = B 2 op = - 25 - δ = β p c PR Tecsup Virtu@l 1.9.7. Sistemas Eléctricos de Potencia COMPENSACIÓN REACTIVA EN LÍNEAS DE TRANSMISIÓN La operación de líneas de transmisión, especialmente aquellas de longitud media y larga, se pueden mejorar por compensación reactiva del tipo serie o paralelo. La compensación serie consiste de un banco de capacitores conectado en serie, con cada conductor de fase de la línea. La compensación paralelo o en derivación, se refiere a la localización de reactores (bobinas) de cada línea al neutro, para reducir parcial o completamente la susceptancia en derivación de las líneas de alta tensión (efecto capacitivo); especialmente en condiciones de baja carga o en vacío, cuando el voltaje en el extremo receptor puede ser muy alto. La compensación serie reduce la impedancia serie de la línea, que representa la causa principal de la caída de voltaje, y el factor más importante en la determinación de la máxima potencia, que la línea puede transmitir. La reactancia deseada de un banco de capacitores se puede determinar, compensando un valor específico de la reactancia inductiva total de la línea. Este criterio conduce a lo que se conoce como el factor de compensación que se define por la relación xC / xL ; xC es la reactancia capacitiva del banco de condensadores; y xL la reactancia total (inductiva), de la línea por fase. Vp jX Capacitor serie L jY/2 jY/2 Reactores en paralelo Fig. 5.18 Compensación reactiva en L.T. - 26 - VR Tecsup Virtu@l Sistemas Eléctricos de Potencia EJEMPLO 3 Se desea estudiar el efecto de los parámetros de la línea, cuando se incluyen los efectos de la compensación serie y la compensación paralelo en líneas de transmisión; para esto se considera un sistema de dos máquinas interconectadas por una línea de transmisión; que puede ser: • • De 230 kV De 400 kV Los datos para estas líneas, son los siguientes: TENSIÓN NOMINAL KV SERIE XL CAPACITANCIA EN PARALELO 230 0.47 Ω / km. 0.29 x 106 Ω - km 345 0.47 Ω / km. 0.241 x 106 Ω - km El sistema representado, se muestra en la siguiente figura: Vtg Vtm jX jXg jXg Eg1 Eg2 jY/2 Xg1 Xg2 Eg1 SB = = = = jY/2 0.5 p.u. (reactancia de secuencia positiva del generador) 0.2 p.u. (reactancia de secuencia negativa del generador) Eg2 1.0 p.u. tensión generada en p.u. 100 MVA. (Potencia de base) Para la línea no compensada, trazar una gráfica del límite de potencia en estado estable, en términos de la reactancia serie. Reconstruir la gráfica para una compensación paralela de 100% (la necesaria para eliminar la capacitancia de la línea), y para una compensación del 50% en 400 kV. - 27 - Tecsup Virtu@l Sistemas Eléctricos de Potencia SOLUCIÓN • Para la línea de 230 kV. La impedancia base, es: Z base = ( 230 ) 2 kV 2 = = 529 Ω 100 S BASE L = Longitud de la línea Km. La reactancia de la línea en por unidad ( PU ) x= 0.47 L 0.47 L = = Longitud de la línea en km. Z base 529 La admitancia en derivación: z base x L Y L = zbase x = 2 2Xc 2XC Y 529 L = p .u . 2 2 x 0.29 x 106 Se define un factor de relación: K = Y /2 529 L 529 = x 6 X 2 x 0.29 x 10 0.47 L K = 1.03 • Para la línea de 345 KV, Se procede de la misma forma. LA IMPEDANCIA BASE, ES : Z Base = (KV )2 = (345)2 SB 100 = 1190,25 Ω LA REACTANCIA DE LA LÍNEA EN P.U. : X p.u. = 0.31 L 0.31 L = zbase 1190.25 - 28 - Tecsup Virtu@l Sistemas Eléctricos de Potencia LA ADMITANCIA EN DERIVACIÓN : Z base x L Y L = Z base = 2 2 Xc 2Xc Y 1190.25 × L = 2 2 x 0.241 x 106 EL FACTOR DE RELACIÓN: K = Y /2 1190.25 L 1190.25 = x = 7.9 6 XC 2 x 0.241 x 10 0.31 L DE LA EXPRESIÓN: K = Y/2 X Y / 2 = KX, es decir que conociendo al coeficiente de relación K, se puede sustituir KX por (Y/2) en los cálculos con lo que se simplifica el sistema; ya que se puede convertir en un sistema serie equivalente, aplicando el teorema de Thévenin. jXg Y = jkX 2 Eg Vo = 1 jKX E g 1 j X g + jKX = Eg 1 KX . Xg Vo = E ' LA CORRIENTE DE CORTO CIRCUITO PARA EL SISTEMA EQUIVALENTE: jXg E´g I cc = Vtg Vo = I CC 1 - 29 - J Xg K X . Xg = j X'g Eg j Xg g Tecsup Virtu@l Sistemas Eléctricos de Potencia Si se obtiene el equivalente de Thevenin en cada lado, el circuito resultante es: jX ´ g 1 jX jX ´ g 2 Eg1 Eg2 La potencia que se transmite, se calcula con la expresión: Pmax = ( X / 2 + x' g 1 ) ( X / 2 + x ' g 2 ) ( X / 2) 2 + ( X / 2 + X ' g1) ( X / 2 + X ' g 2) p.u. USO DE CAPACITORES SERIE: El efecto de los capacitores serie, es la reducción de la reactancia serie efectiva de la línea. Debido a la naturaleza de los parámetros distribuidos de la línea, el número y localización de los capacitores, influirá en los perfiles de tensión a lo largo de la línea; y dará efectos diferentes en la reactancia serie del circuito Π equivalente. Para los propósitos de este problema, se despreciarán estos efectos y se usará el circuito Π, equivalente nominal. Si para la compensación serie, se define la reactancia efectiva requerida como: % compensación serie X ef = X 1.0 100 COMPENSACIÓN PARALELO Si la compensación a realizar es paralela se hace uso de los reactores en paralelo, el efecto de estos reactores será el de cancelar una parte de la capacitancia de la línea; reduciendo el valor de la constante K. Si se deseará eliminar todo el efecto capacitivo, se haría K = 0. El factor de corrección se define como: K ef = K 1 % compensación paralelo 100 Se pueden calcular los valores de x ‘ g1 y x ‘ g2, para distintos valores de K, y de aquí la potencia máxima transmitida, para distintos valores de la reactancia serie en la línea. Para K = 0 y x = 0 x' g1 = x g1 1 k x xg = 1 - 30 - 0 .5 = 0.5 p.u. 0 x 0 x 0 .5 Tecsup Virtu@l Sistemas Eléctricos de Potencia x ' g2 = x g2 1 k x xg 2 = 1 0.2 = 0.2 p.u. 0 x 0 x 0.2 LA POTENCIA MÁXIMA ES: Pmax = x x + x ' g1 + x ' g 2 2 2 p.u. 2 X X X 1 + X 1 g2 + + X g1 2 2 2 Pmax = (0 + 0.5) (0 + 0.2) (0) 2 + (0 + 0.5) (0 + 0.2) = 3.16 p.u. (i) Otro caso para : K = 1.03 X = 0.1 X ' g1 = 0.5 = 0.527 1 1.03 x 0.1 x 0.5 x ' g2 = 0.2 = 0.204 1 1.03 x 0.1 x 0.2 Pmax = Pmax = 2.57 y p.u. p.u. (0.1 / 2 + 0.527) (0.1 / 2 + 0.204) (0.1 / 2) 2 + (0 + 1 / 2 + 0.527) (0.1 / 2 + 0.204) p.u. p.u . Con el mismo procedimiento, se puede elaborar una tabla de resultados como la siguiente: X serie Pmax Pmax K = 1.03 Pmax K = 7.9 0 0.05 0.10 3.16 2.89 2.65 3.16 2.85 2.57 3.16 2.51 1.97 - 31 - Pmax K = 3.95 3.16 2.35 1.73 Tecsup Virtu@l Sistemas Eléctricos de Potencia 0.15 0.2 0.25 0.3 0.35 0.40 0.45 0.5 0.55 0.60 2.43 2.23 2.06 1.91 1.77 1.65 1.55 1.45 1.37 1.29 2.32 2.12 1.94 1.78 1.65 1.52 1.42 1.32 1.24 1.17 1.49 1.0 0.23 0 0 0 0 0 0 0 1.276 0.8597 Gráficamente se puede expresar también, como se indica a continuación: jXg1 jXL jXg2 Eg1 Eg2 jY/2 jY/2 De la gráfica anterior, para la línea de 230 kV, K = 1.03, cuando no está compensada con X = 0.4 P.U., la potencia máxima es de 1.54 P.U. - 32 - Tecsup Virtu@l Sistemas Eléctricos de Potencia Si se usa una compensación serie del 50%. X ef = X 1.0 X ef = 0.2 x% = 0.4 1.0 100 50 100 p.u. p.u. Entonces : Kef = 2 x 1.03 = 2.06 Con estos valores de X y Kef de la gráfica, el límite de potencia es de 1.95 P.U. A esta misma línea, si se le asigna 100% de compensación paralela y no se le asigna compensación sería de la gráfica; los valores serían: X = 0.4 p.u. y K=0 EL LÍMITE DE POTENCIA ES 1.65 P.U. Si ahora, a una potencia transmitida de 1.65 P.U. se le asigna una compensación serie, requeriría de una capacidad de capacitores de: Q = I2 XC = (1.65)2 x 0.2 (p.u.) Q = 0.545 p.u. (MVAR capacitivos) En cambio, si se decidiera asignar el 100% de compensación paralelo; entonces se tendría: Q = (V2 .Y) = (V2 . 2 K X) = 1.0 Q = 0.824 p.u. x 2 x 1.03 x 0.4 (MVAR DE REACTORES) Se observa que para la línea de 230 kV, se tiene mayor ganancia con capacitores serie que con reactores en paralelo, en cuanto a potencia transmitida se refiere. Con relación a la línea de 345 kV, para una X = 0.4 P.U. se analiza la condición de compensación en forma análoga al caso de la línea de 230 kV. El valor de la reactancia , es: 2 0.6 230 X = 0.4 x = 0.142 0.75 345 p.u. Es decir, se refiere a la misma base que la línea de 230 kV; la línea de 345 kV no compensada, tendría un límite de potencia de 1.5 P.U., con 50% de compensación paralela Kef = 3.95 y (x = 0.142), dando un valor Pmax = 2.0 p.u.; los MVAR requeridos en forma de reactor, serían entonces: 1.0 x 2.0 x 3.95 x 0.142 = 1.12 p.u. - 33 - Tecsup Virtu@l Sistemas Eléctricos de Potencia EJEMPLO 4 Se tiene una línea de transmisión de 230 kV con 500 Km de longitud, con los datos calculados en el ejemplo 1.1. Se desea determinar el tamaño de dos bancos de reactores en derivación que se deben colocar en cada extremo; y los cuales deben tener exactamente la misma capacidad, para reducir la generación de potencia reactiva en la línea a cero. SOLUCIÓN Del ejemplo 1.1, los parámetros de la línea son: r = 0.073 Ω / km XL = 0.497 Ω / km YC = 3.173 x 10 –6 SIEMENS / KM / FASE YC / 2 = 1.585 x 10 -6 SIEMENS / KM / FASE El circuito representativo para la línea de 500 km. de longitud. 36.5 j248.5 Zc = 1/1,585x10 -6x1500 jXL jXL Se deben conectar reactores en cada extremo, que tenga una reactancia de: Zc = 1 = − j 1262.6 Ω / fase 1.585 x 10 −6 x 500 XL = j 1262.6 Ω / FASE Considerando que la línea es larga, considérese que el voltaje de operación puede ser el nominal; la capacidad de los reactores en MVAR es, entonces: Qreac = V 2n (230 / 3 ) 2 = = 13.96 MVAR / FASE XL 1262.6 O bien : 13.96 x 3 = 41.9 MVAR trifásico por extremo para la línea total: 83.8 MVAR - 34 - Tecsup Virtu@l Sistemas Eléctricos de Potencia 5.3 EFECTO CORONA Los altos voltajes con que operan las líneas de transmisión producen fuertes campos eléctricos, de tal magnitud que ionizan el aire circundante que está próximo a los conductores de fase. Este efecto, llamado corno es auditivamente detectable como un zumbido y visualmente como una aureola azulina pálida que rodea a los conductores. La intensidad de campo eléctrico crítica EC a la cual principia la ionización para el aire seco es: 0.3 EC = 30 δm 1 + k V/cm δr donde: 3.92 b T δ = densidad relativa del aire = b = presión atmosférica, en cm Hg T = temperatura absoluta, en grados kelvin m = factor de cableado ( 0 < m < 1 ) m = 1, cilíndrico uniforme m = 0.9, ACSR intemperizado r = radio del conductor, cm Si se utilizan conductores enrollados por fase, se tiende a producir un mayor radio efectivo y, por tanto, se reducen los niveles de la intensidad del campo eléctrico en la vecindad del conductor. El efecto corona tiene dos características indeseables: pérdidas de potencia e interferencia o perturbación radioeléctrica. Una expresión para las pérdidas por efecto corona, para una fase y tiempo despejado la obtuvo Peterson como: P= 3.37 × 10-5 fV 2F [log10 (2s /d)]2 kw /fase/milla donde V = voltaje eficaz línea a neutro, en kV f = frecuencia, en Hz F = factor corona determinado por pruebas s = espaciado de fase d = diámetro del conductor La pérdida de potencia es pequeña, valorizada en aproximadamente de de 1 a 2 kW por km, 500 kV, rollo de tres conductores por fase. Sin embargo, las pérdidas corona crecen dramáticamente cuando la línea recibe cualquier forma de precipitación atmosférica, siendo la situación más conflictiva cuando hay heladas. - 35 - Tecsup Virtu@l Sistemas Eléctricos de Potencia Las pérdidas pueden alcanzar valores tan altos como 30 kw/km, con un promedio de 2.4 kw/km esperado, para una línea cuyo diseño sea similar a nuestro ejemplo de 500 kV, localizado en el sudeste de Estados Unidos. La radio interferencia también es un problema y ocurre generalmente sobre una gama de frecuencias de 0.2 a 4 MHz, centrada alrededor de f0 = 0.8 MHz. Las precipitaciones incrementan la interferencia RF, como lo hace la alta humedad. A medida que los conductores envejecen, tienden a decrecer los niveles de interferencia RF. La formulación de ecuaciones generales que respondan para todas las variables pertinentes y que proporcionen resultados exactos es un difícil problema. Los resultados se obtienen usando relaciones empíricas y métodos estadísticos aplicados a cantidades impresionantes de datos registrados. Las pérdidas de potencia por efecto corona y las interferencias RF corona, son dos factores adicionales que se deben considerar cuando se haga el diseño de una línea. 5.4 RESUMEN Se ha observado cómo los campos magnéticos y eléctricos que rodean a la línea de transmisión producen serias caídas de voltaje y corrientes con trayectorias shunt o derivadas, creando la necesidad de insertar elementos inductivos y capacitivos en los modelos de circuitos de línea. Hay muchos interesantes e importantes problemas que están asociados con la operación y diseño de las líneas de transmisión de potencia. De importancia fundamental es la capacidad de la línea de transmisión. Hay dos límites que considerar: el régimen nominal térmico y el límite de estabilidad en estado estacionario. Además, los efectos de impedancia de la línea pueden ocasionar que el voltaje de línea varíe fuera de límites aceptables, resultando altos voltajes en cargas ligeras, y bajos voltajes en cargas nominales. Esta situación se puede remediar mediante la inserción de elementos compensadores en serie lo mismo que en paralelo. El aislamiento de la línea es básicamente determinado al considerar los niveles de voltaje de 60 Hz, sobretensiones inducidas por descargas y sobretensiones inducidas por interconexiones. Tales niveles son referidos como "niveles básicos de impulso aislante" (B.I.L.) y están relacionados con el valor de cresta de la forma de onda de los pulsos de voltaje estándar. Las descargas atmosféricas con la causa más común de que falle la línea (corto circuitos), por lo que es objeto de estudio. Dos técnicas importantes para reducir los efectos dañinos de las descargas atmosféricas son la colocación de neutros aéreos que protejan a los conductores de fase, y la conversación de una baja resistencia entre la base de la torre y el suelo. La respuesta transitoria de línea es un problema analítico muy complicado que hasta muy recientemente se trató casi exclusivamente sobre un dispositivo analógico, conocido como "analizador de circuitos transitorios" (ACT). El ACT es un modelo de circuito, a escala, de laboratorio, que puede simular sistemas simples (unas cuantas líneas y transformadores), e incluye componentes cuyas características alineales fueron comparables a las de los sistemas reales. Ejemplos de los peores casos, en las condiciones de conmutación, pueden rápidamente aislarse por medio de operadores expertos, por lo que proporcionan una información muy útil para el diseño y operación de la línea. Es posible manejar ciertas situaciones simplificadas analíticamente y, usando el mismo procedimiento, extender los métodos para casos más prácticos y complicados. La transmisión de cd es práctica y razonable cuando se tratan grandes distancias. Los efectos corona son indeseables, pues constituyen pérdidas de potencia y fuentes de interferencia. El uso de conductores más largos y enrollados reducirá en cierto grado estos efectos. - 36 - Tecsup Virtu@l Sistemas Eléctricos de Potencia 5.5 PRUEBA DE AUTOCOMPROBACIÓN 1. Considere la L.T. de la configuración mostrada cada fase tiene dos conductores por fase con 40 cm entre conductores y cada conductor tiene una resistencia de 0, 05 Ω/km. Asumir que el radio exterior y el RMG de cada conductor son idénticos e iguales a 1 cm. Asumir una tierra perfecta e ignorando el conductor el conductor a tierra. Estimar: a. R, L, C por km b. Ro, Lo y Co por km Si la línea es operado en 138 KV. Cable de guarda 4m 4m 12m 2. El efecto pelicular SKIN: a. Reduce la resistencia eléctrica b. Aumenta la resistencia eléctrica c. No influye en la resistencia eléctrica d. Aumenta la capacitancia de la línea 3. El efecto inductivo es producto de: a. De la tensión eléctrica b. De la variación de la corriente c. Del material del conductor d. Ninguna de las anteriores 4. El efecto capacitivo permite: a. Elevar la tensión en la recepción b. Reducir la tensión en la recepción c. Reducir la tensión en el envío d. Ninguna de las anteriores - 37 - Tecsup Virtu@l Sistemas Eléctricos de Potencia 5.6 RESPUESTAS A LA PRUEBA DE AUTOCOMPROBACIÓN 1. a) R = 0,025 Ω/km L = 0,90 mH/km C = 0,0127 uF/ km b) R0 = R L0 = 2 mH/km Co = 0,005 62 uF/km 2. b 3. b 4. a FIN DE LA UNIDAD - 38 -