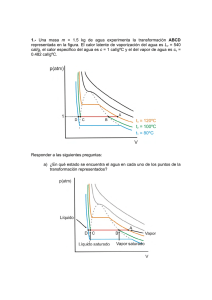
En la tabla se muestran los valores de la presión, volumen y
Anuncio

En la tabla se muestran los valores de la presión, volumen y temperatura que presentan 2 moles 7 de un gas perfecto diatómico, (de coeficiente adiabático γ = ), en algunos de los estados del 5 ciclo A-B-C-D: calentamiento isóbaro enfriamiento isócoro enfriamiento isóbaro compresión isoterma A( PA , V A , T A ) ⎯⎯ ⎯⎯⎯⎯⎯⎯→ B ⎯⎯ ⎯⎯⎯⎯⎯→ C ⎯⎯ ⎯⎯⎯⎯⎯→ D ⎯⎯ ⎯⎯⎯ ⎯⎯ ⎯→ A A P B C VA T TA a) Completar la tabla y dibujar el diagrama P-V b) Calcular los calores específicos a presión constante ( c p ) y PA 2 PA V D a volumen constante ( c v ) en función de R y el 2V A correspondiente valor en cal mol ⋅ K 3TA c) Considerar que la temperatura del estado A es TA = 600 K, y calcular el calor intercambiado en cada etapa, expresando el resultado en función de R y en calorías y la variación de entropía en cada etapa y en el ciclo d) Rendimiento del motor Considerar Ln 3=1.1 Ln 2=0.7 Resolución a) La etapa A-B se produce a presión constante, por lo que la presión de B es igual a la de A; como en la tabla se observa que la temperatura de B es triple que la de A, se deduce que también se triplica el volumen pues VB = P nRTB nR(3T A ) = = 3V A PB PA La etapa B-C se produce a volumen constante, por tanto el volumen de C es VC = V B = 3V A ; de la tabla se desprende que la presión se ha reducido a la mitad, por lo que la temperatura de C es P V TC = C C = nR PA 2 3V A nR A B ½ PA 3 TA 2 = PA D C 2VA 3VA La etapa C-D se produce a presión constante PC = PD = PA , como el volumen de D es 2 PA 2 2V A 2V A , su VA temperatura es TD = PDV D = nR A B C D P PA PA PA 2 PA 2 V VA 3V A 3V A 2V A T TA 3TA 3 TA 2 TA nR = TA V b) A partir del coeficiente adiabático γ = 7 Cp = 5 Cv relación de Mayer C p − Cv = R se obtiene se deduce que C p = 7 Cv , y llevando este valor a la 5 7 2 Cv − Cv = R = Cv . 5 5 Por tanto, los coeficientes en 5R 7R cal y Cp = . Para calcular los correspondientes valores en 2 2 mol ⋅ K cal cal cal sustituimos el valor de R = 2 , de donde C p = 7 y Cv = 5 mol ⋅ K mol ⋅ K mol ⋅ K función de R son C v = c) Si la temperatura de A es 600K, las temperaturas de B, C y D son respectivamente TB =1800K, TC=900K y TD=600K. 7R (1200 K ) = 8400R= 16800 cal , y la 2 T 7R cal = nC p Ln B = 2 mol (1,1) = 7,7 R = 15,4 2 TA K En el proceso A-B, el calor es Q A− B = nC p (TB − T A ) = 2 mol variación de entropía ΔS A− B 5R (−900 K ) = −4500R= −9000 cal y la 2 T 5R cal = nC v Ln C = 2 mol (−0,69) = −3,45R = −6,9 2 TB K En el proceso B-C, el calor es Q B −C = nC v (TC − TB ) = 2 mol variación de entropía ΔS B −C 7R (−300 K ) = −2100R= −4200 cal y la variación de entropía 2 7R cal = 2 mol (−0,41) = −2,87 R = −5,74 2 K En C-D es QC − D = nC p (TD − TC ) = 2 mol ΔS C − D = nC p Ln TD TC Y en D-A Q D − A = nRTD Ln ΔS D − A = nRLn VA VD VA VD = −2mol ⋅ R ⋅ 600 ⋅ 0,7 = −840 R = −1680 cal y la variación de entropía = −2mol ⋅ R ⋅ 0,69 = −1,38R = −2,76 cal K La variación de entropía total del ciclo es ΔS ciclo = 15,4 − 6,9 − 5,74 − 2,76 = 0 d) El rendimiento es el cociente entre el trabajo realizado en el ciclo y el calor absorbido. Por tratarse de un ciclo, no hay variación de energía interna de donde el trabajo del ciclo es igual al calor neto Qneto = Q A− B + Q B −C + QC − D + Q D − A = 16800 − 9000 − 4200 − 1680 cal = 1920 cal η= 1920 = 0.11 16800