Guía - Plataforma Virtual De la Facultad De Ciencias Sede Medellín

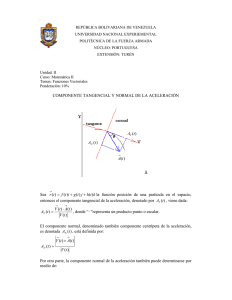
ESCUELA DE FÍSICA
UNIVERSIDAD NACIONAL DE COLOMBIA
SEDE MEDELLÍN
LABORATORIO DE FÍSICA MECÁNICA
PRÁCTICA N° 8
TEMA : MOVIMIENTO CIRCULAR
OBJETIVO GENERAL
• Analizar un movimiento circular uniformemente variado (MCUV) usando cinemática.
OBJETIVOS ESPECÍFICOS
• Llevar a cabo el análisis cinemático del movimiento circular.
• Relacionar la aceleración lineal de un cuerpo con la aceleración tangencial de una polea.
1. FUNDAMENTO TEÓRICO
1.1. MOVIMIENTO CIRCULAR
En muchas situaciones es posible encontrar partículas que se mueven describiendo una trayectoria
circular, esto es conocido como un movimiento circular. Esta situación, como cualquier objeto en
movimiento, puede ser descrito usando los conceptos de cinemática, es decir empleando cantidades
vectoriales como velocidad y aceleración.
Cuando un móvil realiza un movimiento circular desplaza sobre una circunferencia continuamente,
donde hay una aceleración que describe los cambios que se dan tanto en la dirección como en la
magnitud de la velocidad, por lo que resulta útil descomponer esta aceleración en las componentes
paralela y perpendicular a la trayectoria. Los cambios en la magnitud de la velocidad se conocen como
aceleración tangencial, mientras que los cambios en la dirección de la velocidad se conocen como
aceleración centrípeta y esta depende de la velocidad angular. Recordando que la aceleración esta
relacionada con el cambio de velocidad en el tiempo, se puede definir una velocidad tangencial y una
aceleración angular del móvil [1,2]. En la Figura 1 se ilustra el análisis del movimiento de un carro en
una curva.
Figura 1. Automóvil con movimiento circular [2].
Cuando el móvil que describe la trayectoria circular no cambia la magnitud de su velocidad se dice que
el cuerpo describe un movimiento circular uniforme. Tal movimiento no tendrá aceleración tangencial
pero si una aceleración en dirección radial, ya que aunque la rapidez es constante, la dirección de la
velocidad cambia continuamente. Si por el contrario el móvil presenta una aceleración tangencial
constante (la velocidad cambia de magnitud) se conoce como un movimiento circular uniformemente
variado.
El componente de la aceleración tangencial aT , viene dado por el cambio de la magnitud de la
velocidad tangencial por unidad de tiempo (Ecuación 1a) y la velocidad V sería la distancia recorrida
(en este caso una longitud de arco s , ver Figura 2) en un intervalo de tiempo (Ecuación 1b).
dV
dt
ds
V 
dt
aT 
(1a)
(1b)
Figura 2. Representación del movimiento circular en coordenadas polares [1].
2.1
DESCRIPCIÓN CINEMÁTICA DEL MOVIMIENTO CIRCULAR
Para describir la trayectoria del movimiento circular se recomienda usar coordenadas polares ( r ,  )
para definir la posición de la partícula. De esta manera se puede representar el movimiento en
términos del cambio en la posición angular  , ya que el radio de la trayectoria circular r permanece
constante (ver Figura 2). En este sistema de coordenadas se puede definir la velocidad angular  y la
aceleración angular  en términos de la posición angular  como (1,2):

d
dt
(2a)

d 2
dt 2
(2b)
La posición y velocidad de una partícula que describe un movimiento circular uniformemente variado
(con  constante) pueden ser expresadas en función del tiempo transcurrido t con las siguientes
ecuaciones, las cuales son análogas al movimiento uniforme variado:
1
2
  t   0
   t 2  0t   0
(3a)
(3b)
donde  0 y  0 son respectivamente la posición y velocidad angular en el tiempo t  0 . Por último, es
útil tener en cuenta las relaciones entre las cantidades angulares y las cantidades tangenciales s , V y
aT .
s  r
ds
d
r
 r
dt
dt
dV
d
aT 
r
 r
dt
dt
V
(4a)
(4b)
(4c)
2. DESCRIPCION DE LA EXPERIENCIA
En esta práctica se usará la máquina de Atwood (ver Figura 3), y se realizará un análisis cinemático en
este sistema mecánico en el que se observará un movimiento circular uniformemente variado (MCUV)
en una polea. Mediante el análisis anteriormente mencionado se podrá calcular las aceleraciones
involucradas en este sistema mecánico, las cuales son:



La aceleración angular de la polea.
La aceleración tangencial de los puntos de la periferia de la misma (donde se pone la cuerda).
La aceleración lineal con la que desciende la masa m2 (que es igual en magnitud a la
aceleración lineal con la que asciende la masa m1 ).
Figura 3: Máquina de Atwood
Además, se puede esperar que estas aceleraciones en el sistema sean constantes y solo dependan de
los valores de las masas m1 y m2 . Con base en esto se puede afirmar que las masas se desplazan
rectilíneamente con movimiento uniformemente variado, mientras la polea gira con movimiento circular
uniformemente variado. Por tanto, la posición y de la masa m2 se puede hallar como:
y
1
al t 2  V0 t  y0
2
(5)
donde y es posición, y 0 posición inicial, V 0 velocidad inicial, al aceleración lineal y t tiempo. Al
realizar una regresión cuadrática de los datos y vs t se puede hallar el valor de aceleración lineal con
la que cae el cuerpo m2 . Por su parte la posición angular  para el giro de la polea cumple la
ecuación (3a):
1
2
   t 2  0t   0
(3a)
Al realizar una regresión cuadrática de los datos  vs t se puede hallar el valor de aceleración angular
 con la que gira la polea. Si se conoce el radio externo r de la polea, puede calcular la aceleración
tangencial en un punto en la periferia de la polea, según la ecuación (4c).
aT  r
(4c)
Si la cuerda es inextensible y no se desliza sobre la polea, se cumple que la magnitud de la
aceleración tangencial de los puntos del borde de la polea y la magnitud de la aceleración lineal de las
masas m1 y m2 son iguales:
a T  al
(6)
3. TRABAJO PRÁCTICO
El trabajo práctico se dividirá en dos partes: la medición de la aceleración lineal y la medición de la
aceleración angular y tangencial de la polea. Para eso se debe realizarse el montaje mostrado en la
Figura 4, conocido como Maquina de Atwood.

Conectar la fotocompuerta al computador de la siguiente forma: una terminal a un puerto USB
(para alimentar eléctricamente el Diodo Emisor de Luz -LED-) y la otra terminal a la entrada del
micrófono (para entrar la señal de respuesta al PC).

Ejecutar la plataforma de software PhysicsSensor y luego abrir el Sonoscopio Virtual.

Atender la explicación del profesor o del monitor sobre el manejo de este sistema hardwaresoftware.
3.1. MEDIDA DE LA ACELERACIÓN LINEAL
 Ubicar la fotocompuerta de tal forma que el haz de luz sea interrumpido por la caída de la reglacebra, la cual corresponde a la masa que desciende m2 Como se muestra en la Figura 4.
Figura 4. Montaje experimental para medir la aceleración lineal.

Definir como marco de referencia el laboratorio y como sistema de coordenadas un eje y
positivo hacia abajo. Considerar como el instante t  0 al momento en el cual la regla-cebra
comienza a atravesar el haz de luz y la posición de su centro de masa en ese instante es el origen
y 0
de coordenadas ( 0
). Por lo tanto, la posición del centro de masa en cualquier instante se
expresa según la ecuación (5).

Activar el sonoscopio y dejar caer la regla-cebra, asegurando que su recorrido no se vea
interferido por ningún agente externo y que todas las ranuras de la regla cebra generen una señal
(pico) en el sonoscopio. Observar la señal obtenida (sonograma), la cual debe ser similar a la
mostrada en la Figura 5. Recordar que el software da la opción de guardar los datos por si es
necesario un análisis posterior de los mismos).

Mediante un análisis del sonograma obtener los datos de tiempo, cada tiempo t es el intervalo
medido desde el primer pico hasta cada uno de los siguientes picos.

Medir la distancia desde la primera ranura (

Calcular el promedio del tiempo para cada posición.

Reportar la medida de la posición y el tiempo para cada una, con sus incertidumbres en la Tabla 1.
y0  0
) a cada una de las demás ranuras.
Figura 5: Señal desplegada en el sonoscopio debido a las interrupciones del haz de luz de la
fotocompuerta al ser atravesada por la regla-cebra
Tabla 1. Medidas de posición y tiempo

Realizar la regresión cuadrática datos de y vs t . Los puntos de la grafica se ajustan a una
ecuación de forma:
y  a x2  b x  c

(7)
Comparando término a término la ecuación (7) con la ecuación (5) se puede obtener el significado
de cada uno de los coeficientes. Analizando el coeficiente a se puede hallar la aceleración lineal
de la regla como:
al  2a
(8a)
y su incertidumbre esta dada por (DEMOSTRAR):
(8b)
u al = 2u a

a
Esta medida de la aceleración lineal l con su respectiva incertidumbre
el VALOR CONVENCIONALMENTE VERDADERO.
ual
se considerará como
3.2. MEDIDA DE LA ACELERACIÓN TANGENCIAL
 Ubicar la fotocompuerta de tal forma que el haz de luz sea interrumpida por “radios” de la polea,
cuando ésta gira, Como se muestra en la Figura 6.
Figura 6. Montaje experimental para medir la aceleración tangencial
 Definir como marco de referencia el laboratorio y elegir un sistema de coordenadas polares.
Considerar que el instante t  0 la posición angular de alguna de las líneas radiales (que en la
práctica es cualquiera) es  0  0 . Por lo tanto, la posición angular de la polea cualquier instante se
expresa según la ecuación (3a).
 Activar el sonoscopio y dejar caer la regla-cebra, asegurando que su recorrido no se vea
interferido por ningún agente externo. Observar la señal obtenida (sonograma), la cual debe ser
similar a la mostrada en la Figura 7. En este caso la señal es el resultado de las repetidas
interrupciones que hacen los “radios” de la polea al haz de luz de la fotocompuerta. Recordar que
el software da la opción de guardar los datos por si es necesario un análisis posterior de los
mismos).
Figura 7: Señal desplegada en el sonoscopio debido a las interrupciones del haz de luz de la
fotocompuerta al ser atravesada por los radios de la polea
 Mediante un análisis del sonograma se puede medir los instantes para diferentes posiciones
angulares. cada tiempo t es el intervalo medido desde un punto en el primer pico (se elige uno de
los “picos” como el primero) hasta el mismo punto en cada uno de los siguientes “picos”.

Teniendo en cuenta que el patrón de los radios de la polea se repite 10 veces en un giro (cada 36
grados) y este determina la aparición de cada “pico” en la señal, reportar la medida de la posición
angular y el tiempo para cada una, con sus incertidumbres en la Tabla 2.

Realizar la regresión cuadrática datos de  vs t . Los puntos de la grafica se ajustan a una
ecuación de forma:
y  ax2  bx  c

(7)
Comparando término a término la ecuación (7) con la ecuación (3a) se puede obtener el
significado de cada uno de los coeficientes. Analizando el coeficiente a se puede hallar la
aceleración angular de la regla como:
  2a
(9a)
y su incertidumbre esta dada por (DEMOSTRAR):
u = 2u a
(9b)
Tabla 2. Medidas de posición angular y tiempo

Calcular la aceleración tangencial de los puntos del borde de la polea con la ecuación (4c):
aT  r
(4c)
y su incertidumbre esta dada por (DEMOSTRAR):
u aT =

r u 2   u r 2
(4d)
Esta medida de la aceleración tangencial a T con su respectiva incertidumbre u a T se considerará
como el VALOR EXPERIMENTAL.
3.3. PORCENTAJE DE ERROR

Recordando que la aceleración lineal de la regla y la aceleración tangencial de la polea son
iguales en magnitud (ecuación 6), determinar el porcentaje de error usando la ecuación (10).
% Error 
Valor convencionalmente verdadero Valor ex perimental
 100
Valor convencionalmente verdadero
(10)
4. REFERENCIAS
[1]
Serway RA, Jewett JW. Física para ciencias e ingeniería, Volumen 1. 7th ed. Mexico D.F.:
Cengage Learning; 2008. Capítulo 4 y 10, p.84-87,269-275
[2]
Freedman Y, Zemansky S. Física Universitaria. 12th ed. Mexico D.F.: Pearson Educación;
2009. Capitulo 3 y 9. p.87-90, 285-296
Documento elaborado por:
Diego Luis Aristizábal Ramírez
Esteban González Valencia
Tatiana Cristina Muñoz Hernández
Universidad Nacional de Colombia
Sede Medellín
Última revisión: Septiembre/2016