DISEMINACIÓN DE MASAS DE ALTA EXACTITUD POR EL
Anuncio

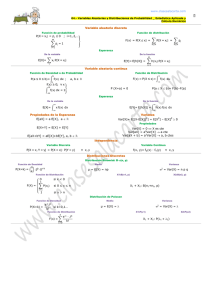
DISEMINACIÓN DE MASAS DE ALTA EXACTITUD POR EL METODO DE GAUSS MÁRKOV DESDE 1 mg HASTA 1 kg Expositora: Luz Cori A. Fecha 2012-05-17 1. MINIMOS CUADRADOS ORDINARIOS - MCO Y GAUS MARKOV - GM 1.1. Modelo Matemática MCO-GM En este modelo de diseminación se realiza una serie de comparaciones que a su vez genera un número igual de ecuaciones en donde las incógnitas son los valores de masa de las pesas (a excepción de la pesa patrón involucrada), generalmente estos modelos se usan por décadas de 1 kg a 100 g, de 100 g a 10 g , … ó de 1 kg a 10 kg • La solución de estos sistemas de ecuaciones implica un mayor número de mediciones y el uso de matemáticas más complejas que para la calibración de pesas por comparación una a una, sin embargo, debido a la necesidad de generar la escala de masa a partir de 1 kg y a la posibilidad de obtener resultados muy confiables al introducir patrones de control, estos métodos son recomendados para la calibración de pesas clase OIML E1 1.2. Mínimos cuadrados Ordinarios - MCO En este método, se analizaran los principales supuestos del estimador de mínimos cuadrados ordinarios paso a paso donde se demuestra cada supuesto de: linealidad, esperanza nula, insesgadez, ausencia de autocorrelación, matriz de varianza y covarianza, en presencia de una matriz de varianza y covarianza de los errores, para llegar al menor estimado. Para este método consideramos el modelo lineal general, Y X (1) donde es el error, es el mejor estimado del modelo lineal y X es la matriz de diseño, y la matriz columna “ Y “ se obtiene de la siguiente ecuación yi mi ai Vp Vx i donde: mi ai Vp Vx i es la diferencia del patrón y la muestra de un ciclo de mediciones es la densidad del aire por la suma de volúmenes de la pesas del patrón y la muestra Supuestos del Estimador de Mínimos Cuadrados Ordinarios S1-Linealidad: Y X sigue siendo lineal en el vector de parámetros β y la El modelo variable dependiente Y es una función lineal de β , tal como se observa en la siguiente ecuación: T T X YX Xβ X X T 1 T T X Y X X 1 T β XTX X Xβ 1 (2) X TY Para comprobar que los parámetros estimados son una combinación lineal de las perturbaciones aleatorias del modelo basta con sustituir Y por su expresión completa (ecuación 2) Entonces tenemos: XY β X X X ( X ) β X X X X X X β XTX 1 T 1 T T T 1 T T 1 β XTX X T 1 X T (3) S2-Esperanza nula otro supuesto de MCO indica que matemáticamente es cero. es el error del ajuste, cuya esperanza E ( ) 0 S3-Insesgadez En primer lugar, contar con un estimador insesgado nos asegura que el valor esperado de nuestro cálculo coincide con el valor real del parámetro. Este requisito es fundamental a la hora de realizar una estimación. Partiendo de la ec. (3) X E ( β ) E X X X E ( β ) E X X X E ( ) β XTX 1 T 1 T T E( β) 1 T T E ( ) 0 (4) Entonces se cumple la insesgades tal como se muestra en la ecuación (4) S4-Ausencia de autocorrelación Este supuesto indica que la variable y las perturbaciones no están correlacionadas es decir no existe autocorrelación entre los errores; por lo tanto la covarianza (Cov) de los errores es igual a cero, = 0 , lo cual implica que no existe autocorrelación en la variable dependiente, es decir, Cov (Yi , Yj ) = 0. cov( t , ) E ( t E ( t ))( E ( )) E ( t )( E ( )) E[( t ) ] E[( t ) E ( )] E ( t ) cov( t , ) E ( t ) E ( ) 0 (t ) (5) S5-Matriz de varianza covarianza Var ( t ) E t E ( t ) 2 Var ( t ) E ( t2 ) (t 1,2,..., n) Llevándolo a su forma matricial : E ( T ) donde fi es un valor arbitrario. (6) Varianza del estimador : Para obtener la mínima varianza de MCO se obtiene la varianza del estimador var( β ) E ( β - E( β ))( β - E( β )) T usando la ecuación (4) tenemos var( β ) E ( β - )( β - ) T Usando la ecuación (3) tenemos β XTX 1 X T var( β ) E X T X X T 1 X T X 1 X T T var( β ) X T X X T E ( T ) X T X 1 X 1 T T T T var( β ) X X X X E ( ) X X 1 1 I de la ecuación (6) se tiene fi: var( β ) X X T 1 var( β MCO ) X T X 1 El método de MCO no es el mejor estimado de la mínima varianza por el valor arbitrario que proporciona este método. Por esta razón se dice que MCO no es eficiente. Se puede obtener la mínima varianza de var( β ) solo si : 2 I donde : 2I (Yi X i )(Yi X i ) T .I n p Siendo una matriz simétrica, definida positiva. y es homocedastica y no correlativa, entonces, se tendría: var( β ) 2 X T X 1 Como se menciono anteriormente aquí no se ha demostrado que sea homocedastica, en GM se demostrara este supuesto. 1.1. Metodo de Gauss Markov GM El Metodo de Gauss Markov afirma que la estimación por mínimos cuadrados generalizados del modelo teórico de regresión es óptima en el sentido de que hace mínimo el módulo del vector de residuos (mínima varianza). S6-Supuesto de Homocedasticidad Se dice que existe homocedasticidad cuando la varianza de los errores de la regresión es la misma para cada observación i (de 1 a n observaciones), es decir: E ( i2 ) 2 i 1, n 2 donde es un escalar constante para todo i. Lo que significaría que habría una distribución de probabilidad de idéntica amplitud para cada variable aleatoria. Esta cualidad es necesaria, según el teorema de Gauss Márkov, para que en un modelo los coeficientes estimados sean los mejores o eficientes, lineales e insesgados. Entonces la varianza de es la misma para todas las observaciones Var ( t ) E t E ( t ) 2 Var ( t ) E ( t2 ) 2 (t 1,2,..., n) En el modelo la matriz de varianzas de los errores es de la forma (7) E ( T ) 2 I Entonces homocedasticidad significa igual dispersión, en otras palabras significa que las poblaciones Y correspondientes a diversos valores de X tienen la misma varianza 2 . Transformando el modelo inicial que se cumplan todos los homocedasticidad) Definimos la matriz Y X supuestos de una forma conveniente de modo de Gauss Markov (supuesto de como simétrica y positiva. Ahora esta matriz debe ser igual a una matriz Q que es simétrica y no singular. Entonces definimos la matriz con las siguientes propiedades: QQ (8) Se considera la siguiente transformación del modelo lineal general multiplicando por Q 1 Y X Y * Q 1Y Q 1Y Q 1 X Q 1 X * Q 1 X Y * X * * * Q 1 Ahora nos queda verificar que el modelo transformado de esta forma cumpla con todos los supuestos del teorema de Gauss Markov Linealidad: el modelo sigue siendo lineal dado que Esperanza nula: Y * es función lineal de β E ( * ) E (Q 1 ) Q 1 E ( ) 0 0 Para cumplir con el supuesto de homocedasticidad recurrimos a la ecuación (7) donde: T 1 * E ( * * ) E (Q 1 (Q 1 )T ) Q 1 E ( T )Q 1 Q QQQ 1 I I NOTA: Como Q es una matriz simétrica se cumple que I Q QT El estimador de mínimos cuadrados generalizados (MCG) se define como el estimador de mínimos cuadrados ordinarios de en el modelo transformado: β MCG X *T X 1 * 1 T T X* Y* 1 1 1 T 1 β MCG (Q X ) (Q X ) (Q X ) (Q Y ) 1 β MCG T 1 1 X Q Q X X T Q 1Q 1Y 1 1 β MCG X T 1 X 1 X T 1Y (9) El estimado β MCG se puede escribir también como: 1 T β MCG X X 1 T β MCG X T 1 X 1 X ( X ) 1 X T 1 Ahora calculamos la varianza del estimado de mínimos cuadrados generalizados β MCG Var ( β MCG ) E ( β - E( β ))( β - E( β )) T (10) Para el cálculo de Var ( β MCG ) recurrimos a la ecuación por insesgades del modelo lineal se tiene: E( β MCG ) Ahora remplazamos la ecuación anterior de insesgades en la ecuación (10) Var ( β MCG ) E ( β - )( β - ) T Var ( β MCG ) E X T 1 X Var ( β MCG ) X T 1 X 1 1 X T 1 X T 1 X 1 X T 1 X T 1 E ( T ) X 1 X T 1 X 1 Var ( β MCG ) X T 1 X X T 1 X 1 X T 1 X I I 1 1 T Var ( β MCG ) X T 1 X 1 (11) 2. CALCULO DE LA COMPONENTE Y CALCULO DE LA COMPONENTE Y . La incertidumbre por indicación de la balanza debida a la resolución y desviación de la balanza y I . f s (mP P ). X Pi ai .V i I u (d ) u A ( I ) I resolución I desviación Incertidumbre por el factor de sensibilidad de la balanza ( f s ) Para balanzas electrónicas se asume que su incertidumbre es despreciable u( f s )= 0 La incertidumbre combinada de la pesa patrón . u m cP u 2 m cPcert u 2 m cP Incertidumbre por la Densidad del aire: La incertidumbre debido a la corrección por empuje del aire será calculada de la siguiente forma 2 2 P i i m ni u 2 P 2 u i ˆ uE i m cP u a a o a o a o 2 al o 4 m nP P4 P i i La incertidumbre del volumen de la masa patrón y la masa a calibrar u 2 (V ) ( u 2 (V ) u 2 (V )) Para calcular la incertidumbre de y derivamos cada una de sus componentes, tal como se muestra a continuación y I . f s (mP P ). X Pi ai .V i Y1 Y2 Y3 2 I f s 2 I f s 2 u 2 (Y1 ) u ( I ) u ( fs ) ( I ) ( f ) s 2 2 2 2 X P2 u 2 (mP ) X P2 u 2 ( P ) 2 fs . u (I ) I . u ( f s ) 2 2 2 2 X P2 ( u 2 (mP ) u 2 ( P )) 2 f s . u (resl ) u ( rept ) I . u ( f s ) . 2 2 a V 2 a V 2 u 2 (Y3 ) u ( ) u (V ) a (V ) ( a ) 2 V 2 . u 2 ( a ) a . u 2 (V ) 2 V 2 . u 2 ( a ) a ( u 2 (V ) u 2 (V )) es el error del ajuste, cuya esperanza matemáticamente es cero y varianza 2 entonces : 2 u( y) f s .u 2 (resl) u 2 (rept) I 2 . u 2 ( f s ) u 2 (mP ) u2 ( P )X P2 2 2 V 2 . u 2 (a ) a (u 2 (V ) u 2 (V )) 2 u( y) 2 mP X P 2 P X P 2 u (Y2 ) u ( m ) P ( ) u ( P ) ( m ) P P 2 2 Var ( β MCG ) X X T 1 1 2 (Yi X i )(Yi X i )T n p 3. APLICACIÓN DEL METODO DE GM EN LA CALIBRACION DE PESAS E1 Comparadora de masas requerida para hacer una década de pesas de alta exactitud E1 METTLER TOLEDO AX 106 Resolución de 0,001 ug Capacidad máxima 111 g Como hacer una década Ejemplo con el método de GM De 100 g a 10 g MATRIZ yi =comparaciones de patron (-1) con la muestra (1) 100 g E0 y1 y2 y3 y4 y5 y6 y7 y8 y9 y10 y11 y12 y13 -1 -1 -1 0 0 0 0 0 0 0 0 0 0 100 g E1 1 0 0 -1 -1 0 0 0 0 0 0 0 0 50 g E1 0 1 1 1 1 -1 -1 0 0 0 0 0 0 20 g E1 20 g (.) E1 0 1 1 1 1 1 1 1 1 0 -1 -1 0 0 1 1 1 1 1 1 -1 -1 -1 0 1 0 10 g E1 0 1 0 1 0 1 0 1 -1 1 1 0 -1 10 g (pv) E0 0 0 1 0 1 0 1 -1 1 1 1 0 1 Datos de para la calibración de pesas CALIBRACIÒN DE PESAS POR EL METODO DE GM - DISEMINACIÓN DE PESAS E0 E1 E1 E1 E1 E1 E0 Valor nominal valor de masa g 100 g 100 g 50 g 20 g 20 g (.) 10 g 10 g (pv) mg Incertidumbre estándar -0,0778 mg 0,0072 -0,0066 0,004 Volumen Incertidumbre volumen cm3 12,438 12,4898 6,2467 2,498 2,4984 1,2491 1,2445 cm3 0,0040 0,004 0,0020 0,0016 0,0016 0,0012 0,0015 Calibración de pesas por el método de GM de una década y m aVx Vp decadas y1 y2 y3 y4 y5 y6 y7 y8 y9 y10 y11 y12 y13 (g) 100 100 100 100 100 50 50 30 30 20 20 20 10 m densidad del aire (mg) mg/cm3 -0,009 1,16768138 -0,010 1,16805527 -0,021 1,16825329 -0,002 1,16778308 -0,016 1,16686444 0,023 1,16559560 0,012 1,16447456 0,0007 1,16247540 -0,025 1,16291314 0,010 1,16056822 0,021 1,16062615 0,014 1,16126413 -0,014 1,16170532 -0,0778 mg incertidumbre densidad del aire mg/cm3 0,00096811 0,00096842 0,00096859 0,00096820 0,00096744 0,00096638 0,00096545 0,00096380 0,00096416 0,00096222 0,00096226 0,00096279 0,00096316 V V cm3 0,05180 0,05420 0,04960 0,00240 -0,00220 -0,00120 -0,00580 0,00420 -0,00500 -0,00480 -0,00440 0,00040 -0,00460 Y (mg) 0,051 0,054 0,037 0,001 -0,019 0,022 0,005 0,006 -0,031 0,004 0,016 0,014 -0,019 -0,0778 Calibración de pesas por el método de GM de una década Resultados MASA (g) CORRECCION ( mg ) -0,078 -0,023 -0,023 -0,012 0,001 0,011 -0,007 100 g E0 100 g E1 50 g E1 20 g E1 20 g (.) E1 10 g E1 10 g E0 T 1 β MCG X X 1 INCERTIDUMBRE (mg) k=1 k=2 0,0036 0,007 0,0066 0,013 0,0039 0,008 0,0023 0,005 0,0023 0,005 0,0017 0,003 T 1 X Y Var ( β MCG ) X T 1 X 1 GRACIAS POR SU ATENCION