Circunferencia y círculo - Instituto Inmaculada Concepción
Anuncio

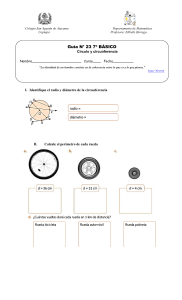
INSTITUTO INMACULADA CONCEPCION VALDIVIA GUIA DE MATEMATICA 8º 2015 Nombre_____________________ Fecha: _______ Curso: 8° AÑO ___ Profesor: FELIPE SILVA OPORTO; Objetivos Cognitivos: Capacidad: Razonamiento Lógico Destrezas : calcular, resolver problemas Objetivos Afectivos: Valor: Respeto Actitud: responsabilidad Contenidos: circunferencia y círculo. Calcular el perímetro o longitud de las siguientes circunferencias, realizando los cálculos correspondientes en tu cuaderno. Trabajando con responsabilidad. a) La longitud de las siguientes circunferencias. (𝜋 = 3,14) b) ¿cuál el diámetro de una circunferencia de 12,56 m de longitud? c) ¿cuál el diámetro de una circunferencia de 47,1 cm de longitud? d) ¿cuál es el radio de una circunferencia de 69,08 cm de longitud? Calcular el área de las siguientes circunferencias, realizando los cálculos correspondientes en tu cuaderno. Trabajando con responsabilidad. b) a) c) 12 cm 20 cm 7 m e) f) 30 cm 10 cm d) 3,5 cm h) 18,7 m g) 15 m Resolver problemas referidos a perímetro de una circunferencia y área de un círculo, realizando los cálculos correspondientes en tu cuaderno. Trabajando con responsabilidad. a) ¿Cuál es el diámetro que tienen las ruedas de un coche si al dar 20 vueltas el coche avanza 37,68 m? (considere π=3,14) b) Diez bomberos sujetan por el borde una lona circular. Cada bombero abarca 1,57 m del borde de la lona ¿Cuánto mide el radio de dicha lona? c) Sandra y David están jugando con sus yo-yos. Los dos yo-yos tienen la cuerda igual, de 75,36 cm de longitud, pero el centro del yo-yo de Sandra tiene 2 cm de diámetro y el de David tiene 3 cm. (considere π=3,14) ¿cuántas vueltas dan el yo-yo de Sandra y el de David con esta longitud de cuerda? d) Se están confeccionando manteles y centros de mesa en forma de círculo. Cada uno lleva cinta en el borde. Se desea saber en la forma más precisa posible ¿Cuántos metros de cinta y género se requieren para cada uno? Los diámetros son: centro de mesa 40 cm y mantel 1,20 m. (considere π=3) e) Si el radio en una circunferencia aumenta al doble, al triple, etc., ¿cómo aumenta el perímetro correspondiente? ¿Es posible afirmar que la relación entre el radio y el perímetro correspondiente es proporcional? ¿Por qué? f) Si el radio en una circunferencia se aumenta al doble, tiple, etc. , ¿cómo aumenta el área correspondiente? ¿Cómo se puede caracterizar el aumento del área del círculo? ¿Es posible afirmar que la relación entre el radio y el área correspondiente es proporcional? ¿Por qué? g) La tierra está a una distancia del sol de 155 millones de km. aproximadamente. La trayectoria de la Tierra alrededor del Sol es casi circular. 1) ¿Qué distancia recorremos "en órbita" alrededor del Sol cada año? (considere π=3) 2) ¿Cuál sería la velocidad de la Tierra en su órbita? h) ¿Cuál es el perímetro de la circunferencia si el rectángulo está inscrito en la circunferencia y su lado mayor mide 12 cm y el menor 9 cm?