Los números complejos
Anuncio
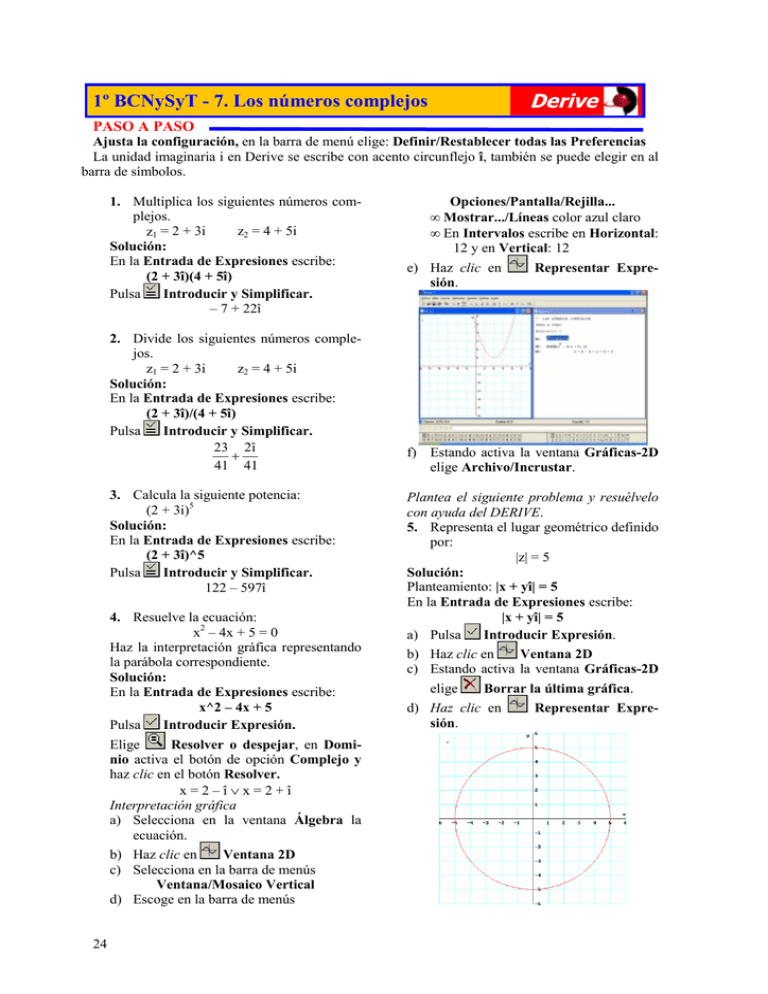
1º BCNySyT - 7. Los números complejos Derive PASO A PASO Ajusta la configuración, en la barra de menú elige: Definir/Restablecer todas las Preferencias La unidad imaginaria i en Derive se escribe con acento circunflejo î, también se puede elegir en al barra de símbolos. 1. Multiplica los siguientes números complejos. z2 = 4 + 5i z1 = 2 + 3i Solución: En la Entrada de Expresiones escribe: (2 + 3î)(4 + 5î) Pulsa Introducir y Simplificar. – 7 + 22î 2. Divide los siguientes números complejos. z2 = 4 + 5i z1 = 2 + 3i Solución: En la Entrada de Expresiones escribe: (2 + 3î)/(4 + 5î) Pulsa Introducir y Simplificar. 23 2î + 41 41 3. Calcula la siguiente potencia: (2 + 3i)5 Solución: En la Entrada de Expresiones escribe: (2 + 3î)^5 Pulsa Introducir y Simplificar. 122 – 597î 4. Resuelve la ecuación: x2 – 4x + 5 = 0 Haz la interpretación gráfica representando la parábola correspondiente. Solución: En la Entrada de Expresiones escribe: x^2 – 4x + 5 Pulsa Introducir Expresión. Elige Resolver o despejar, en Dominio activa el botón de opción Complejo y haz clic en el botón Resolver. x=2–î∨x=2+î Interpretación gráfica a) Selecciona en la ventana Álgebra la ecuación. Ventana 2D b) Haz clic en c) Selecciona en la barra de menús Ventana/Mosaico Vertical d) Escoge en la barra de menús 24 Opciones/Pantalla/Rejilla... • Mostrar.../Líneas color azul claro • En Intervalos escribe en Horizontal: 12 y en Vertical: 12 Representar Expree) Haz clic en sión. f) Estando activa la ventana Gráficas-2D elige Archivo/Incrustar. Plantea el siguiente problema y resuélvelo con ayuda del DERIVE. 5. Representa el lugar geométrico definido por: |z| = 5 Solución: Planteamiento: |x + yî| = 5 En la Entrada de Expresiones escribe: |x + yî| = 5 Introducir Expresión. a) Pulsa b) Haz clic en Ventana 2D c) Estando activa la ventana Gráficas-2D elige Borrar la última gráfica. d) Haz clic en sión. Representar Expre- ASÍ FUNCIONA Operaciones con números complejos Se escribe la operación en la barra de Entrada de Expresiones y se elige la opción Simplificar. Introducir y Resolver ecuaciones con raíces complejas Resolver o despejar, en Dominio se activa el botón de opEn la barra de herramientas se elige ción Complejo y se hace clic en el botón Resolver. Parte real y parte imaginaria de z re(z) es la parte real im(z) es la parte imaginaria PRACTICA 6. Sea z1 = 5 – 4i, z2 = – 2 + 3i Calcula: a) z1 + z2 b) z1 – z2 d) – 5z1 + 9z2 c) 7z1 – 4z2 7. Sea z1 = 3 + 5i, z2 = 4 – 2i, z3 = – 1 + 6i Calcula: a) z1 · z2 b) z1 · z3 c) z2 · z3 8. Calcula: a) (3 + 2i)7 c) (2 – i)9 b) (– 4 + 7i)8 d) (1 + i)10 9. Sea z1 = 5 + 6i, z2 = 8 – 9i, z3 = – 4 + 3i Calcula: b) z1/z3 c) z2/z3 a) z1/z2 10. Resuelve las siguientes ecuaciones: b) z2 = – i a) z2 = – 3 3 c) z = 1 d) z3 = i 11. Resuelve las siguientes ecuaciones: b) z4 = – 81 a) z4 = 81 4 2 c) z + 5z – 36 = 0 d) z4 + 13z2 + 36 = 0 Plantea los siguiente problemas y resuélvelo con ayuda del DERIVE. 14. Hallar una ecuación de segundo grado que tenga las raíces complejas conjugadas 3 ± 4i 15. Halla una ecuación de segundo grado que tenga las raíces: 6 ± 5 i 16. Representa el lugar geométrico definido por: 1 < re(x + îy) < 3 ¿Qué se obtiene? 17. Representa el lugar geométrico definido por: – 2 < im(x + îy) < 3 ¿Qué se obtiene? 18. Representa una corona circular de centro el origen de coordenadas y de radios 3y5 19. Mediante ensayo-acierto halla la fórmula de la siguiente parábola. 12. Resuelve la ecuación: x2 – 6x + 13 = 0 Haz la interpretación gráfica representando la parábola correspondiente. 13. Resuelve la ecuación: x2 + 4x + 5 = 0 Haz la interpretación gráfica representando la parábola correspondiente. 25