Guía de estudio de Matemática para Segundo año Presentación

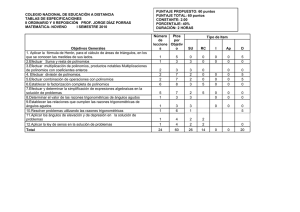
Guía de estudio de Matemática para Segundo año
Presentación
Sentir satisfacción por el logro de un aprendizaje es una experiencia que tienes que vivirla.
Desarrollar bien esta guía de estudio es una oportunidad para alcanzar esas experiencias.
Objetivos
1. Elaborar argumentos matemáticos mediante el uso de enunciados y teoría de exponentes.
2. Transformar en matemáticas realidades comunes de ángulos formados por dos rectas paralelas
cortadas por una secante.
3. seleccionar y utilizar decimales y fracciones en resultados y modelos matemáticos.
4. Discriminar y seleccionar adecuadamente el grado absoluto y relativo de polinomios y efectuar
la adición y sustracción de estos.
Contenidos y fuentes de estudio
1. Teoría de exponentes
2. Ángulos formados por
dos rectas paralelas
cortadas por una
secante.
3. Números racionales
4. Monomios y polinomios
Cuaderno de trabajo páginas 10
Cuaderno de trabajo páginas 29 (2), 30
Cuaderno de trabajo páginas 42 (1,2,3 y 8), 43(3 al 12)
Cuaderno de trabajo páginas 24(4), 25(1 y 2), 47(2,3 y 8), 48 (1 y 3) y
50(1,3 y 5).
Orientaciones para el estudio
1. Teoría de
exponentes
2. Ángulos
formados
por dos
rectas
paralelas
cortadas por
una secante.
Estudiar las propiedades de la teoría de exponentes página 18 del libro y elaborar
un ejemplo para cada propiedad.
Resolver los ejercicios de la página 10 del cuaderno de trabajo aplicando la teoría
de exponentes.
En los siguientes esquemas poner letras en los ángulos y luego mencionar que
letras forman ángulos alternos externos, conjugados externos, alternos internos,
conjugados internos y correspondientes.
Utilizando las propiedades de los ángulos formados por dos paralelas y una
secante resolver ejercicios de la página 29(2) y 30 del cuaderno de trabajo.
En el siguiente mapa señale el nombre de 3 calles que formen 2 paralelas y una
secante, ubica puntos en esas calles y señala ángulos alternos externos,
conjugados externos, alternos internos, conjugados internos y correspondientes.
3. Números
racionales
5. Operaciones
con
polinomios
Determinar la expresión decimal de una fracción, dividiendo el numerador entre el
denominador y de acuerdo al cociente determinar si es una expresión decimal
exacta, periódica pura y periódica mixta. Poner 3 ejemplos para cada caso.
Desarrollar los ejercicios del cuaderno de trabajo página 42(8) sobre expresiones
decimales.
Lee cuidadosamente el enunciado de los problemas de fracciones de la página 42
(2, 3 y 8), 43(3 al 12) y resuélvelos (no olvides que un problema puede resolverse
de varias maneras).
Adicionalmente resuelve los siguientes problemas.
a) Halla la fracción equivalente a 7/12 cuya suma de sus términos es 95. Dar
como respuesta la diferencia de sus términos de la fracción equivalente.
b) ¿Cuántos dieciseisavos hay en 5/8?
c) ¿Cuál es la fracción ordinaria que resulta triplicada si se agrega a sus dos
términos su denominador?
d) En una clase de “e” estudiantes la tercera parte de los ausentes es igual a
la séptima parte de los presentes. ¿Qué fracción de los estudiantes
estuvieron ausentes?
e) En una reunión habían 30 parejas bailando, además 40 hombres y 10
mujeres estaban sentadas, entonces ¿Qué parte de los reunidos es el
número de mujeres?
f) Se tiene una fracción 3/8 ¿Qué cantidad se debe sumar al numerador y
denominador para que la fracción sea 5/6?
g) En una reunión la cuarta parte son hombres, de los cuales la tercera parte
son solteros y 10 son casados ¿Cuántas mujeres hay en dicha reunión?
h) La distancia recorrida por un móvil se calcula multiplicando la velocidad
por el tiempo ¿Cuál es la distancia recorrida por un móvil en un tiempo de
9 horas a una velocidad de 14,88…. Km/h?
i) Halla el producto de los cocientes que se obtienen al dividir 4,0625 por
3,75 y 36,111… por 8,333….
j) Se tienen azulejos de forma rectangular de dimensiones 6,222…cm x
5,185185… cm con las cuales se quiere cubrir la menor área de forma
cuadrada. ¿Cuántos de estos azulejos serían necesarios?
Escribe un monomio y un polinomio y determina sus términos.
Establece diferencias entre el grado absoluto y relativo de monomios y polinomios.
Resolver ejercicios del cuaderno de trabajo página 24 (4) y 25 (1 y 2).
Recuerda las técnicas operativas de la adición y sustracción de polinomios a través
de 3 ejemplos de aplicación sobre adición y sustracción. De polinomios.
Resuelve los ejercicios de la página 47(2,3 y 8), 48 (1 y 3) teniendo cuidado de los
signos y de los denominadores.
Efectúa operaciones combinadas de adición y sustracción en el cuaderno de
trabajo página 50(1,3 y 5).
Observa y lee cuidadosamente los siguientes problemas y resuélvelos.
a) Describe el área de la figura a través de una expresión algebraica
1cm
4cm
a
a
a
a
a
a
1 cm
b) El médico francés Pablo Broca estableció una tabla de peso para adultos.
¿Cómo se calcula, según Broca, el peso normal en Kg si la persona mide x cm?
¿Por qué factor se debe multiplicar el peso normal para obtener el peso ideal de
los hombres (mujeres).
Escribe una expresión con la variable x que te permita calcular el peso ideal de
una persona que tiene un tamaño de x cm.
El señor Fernández pesa 72 Kg. El sostiene que éste es su precio ideal ¿Cuánto
mide? ¿Cómo calculaste?
Tabla en peso según Broca
Tamaño en cm
Peso normal en Kg
Peso ideal en Kg
Hombres
Mujeres
160
60
54,0
51,0
162
62
55,8
52,7
164
64
57,6
54,4
166
66
59,4
56,1
168
68
61,2
57,8
170
70
63,0
59,5
172
72
64,8
61,2
174
74
66.6
62,9
El peso ideal para hombres se encuentra 10% debajo del peso normal, para las
mujeres se encuentra 15% debajo del peso normal.
c) Cuanto más lejos se encuentra el rayo durante una tormenta, más tarde se
escucha el trueno. Si se divide entre 3 el tiempo en segundos existente
entre el relámpago y el trueno, se obtiene la distancia aproximada a la que
se encuentra el rayo en km. Indica una expresión para el cálculo de la
distancia a la que se encuentra el rayo, si se conoce el tiempo.
d) Un área cuadrada debe ser rodeada por planchas de cemento.
¿Cuántas planchas se necesitan? Indica una expresión para esto.
e) En un paralelepípedo rectangular, la altura es 3 veces mayor que el lado
de la base cuadrada. Expresa el largo total de todas las aristas mediante
una expresión algebraica.
Evaluación
La evaluación será en base a las capacidades del área: Razonamiento y demostración (utiliza el
conocimiento matemático para analizar situaciones y dar solución a ejercicios, preguntas y
problemas), Comunicación matemática (dominio de algoritmos y propiedades) y Resolución de
problemas (dar solución con una respuesta clara a diferentes situaciones).
1. Teoría de exponentes
2. Ángulos formados por dos
rectas paralelas cortadas
por una secante.
3. Números racionales
4. Operaciones con
polinomios
Aplicar el correcto uso de la teoría de exponentes para la solución de
ejercicios.
Resuelve ejercicios sobre ángulos formados por 2 paralelas y una
secante.
Resuelve problemas sobre fracciones y decimales.
Halla el grado absoluto y relativo de monomios y polinomios.
Resuelve problemas y ejercicios combinados de adición y
sustracción de polinomios.