ESTUDIO DE UN MOVIMIENTO RECTILINEO Y UNIFORME (1

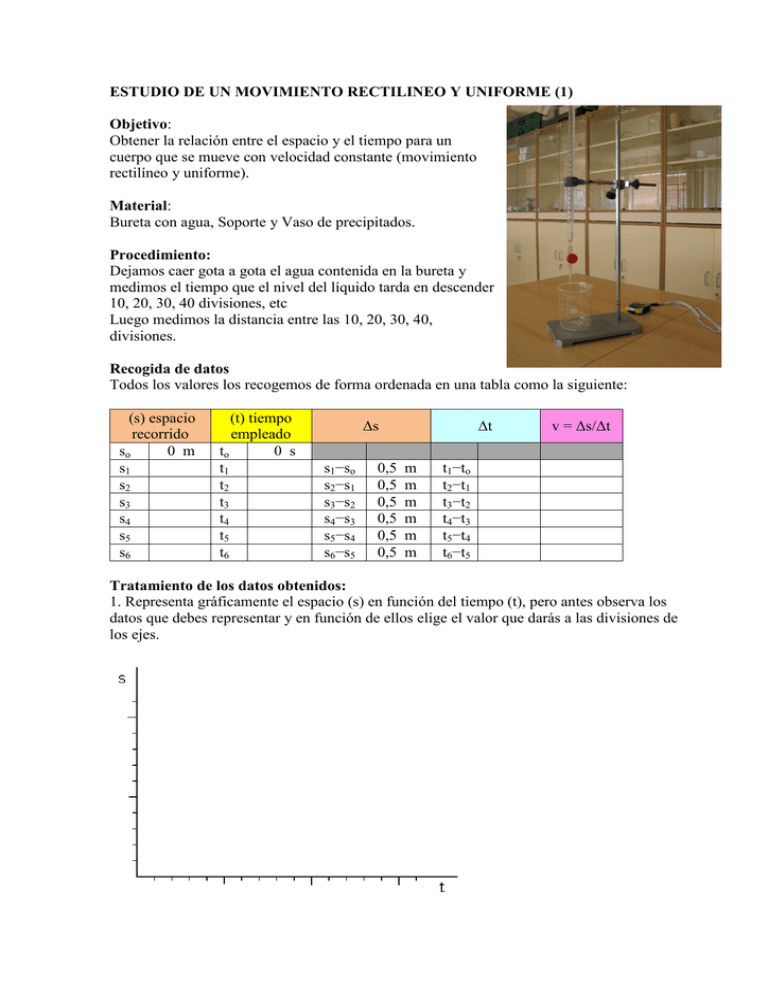
ESTUDIO DE UN MOVIMIENTO RECTILINEO Y UNIFORME (1)
Objetivo:
Obtener la relación entre el espacio y el tiempo para un
cuerpo que se mueve con velocidad constante (movimiento
rectilíneo y uniforme).
Material:
Bureta con agua, Soporte y Vaso de precipitados.
Procedimiento:
Dejamos caer gota a gota el agua contenida en la bureta y
medimos el tiempo que el nivel del líquido tarda en descender
10, 20, 30, 40 divisiones, etc
Luego medimos la distancia entre las 10, 20, 30, 40,
divisiones.
Recogida de datos
Todos los valores los recogemos de forma ordenada en una tabla como la siguiente:
(s) espacio
recorrido
so
0 m
s1
s2
s3
s4
s5
s6
(t) tiempo
empleado
to
0 s
t1
t2
t3
t4
t5
t6
∆s
s1−so
s2−s1
s3−s2
s4−s3
s5−s4
s6−s5
0,5
0,5
0,5
0,5
0,5
0,5
∆t
m
m
m
m
m
m
v = ∆s/∆t
t1−to
t2−t1
t3−t2
t4−t3
t5−t4
t6−t5
Tratamiento de los datos obtenidos:
1. Representa gráficamente el espacio (s) en función del tiempo (t), pero antes observa los
datos que debes representar y en función de ellos elige el valor que darás a las divisiones de
los ejes.
2. Representa gráficamente la velocidad (v) en función del tiempo (t).
3. Junto a cada gráfica haz una interpretación de la misma y encuentra la relación
matemática que relaciona a las dos variables.
Cuestiones:
1. En este experimento el móvil no ha sido un coche, ni una bola. ¿Cuál ha sido el móvil en
esta práctica?
2. Cuáles son las ecuaciones de la aceleración, velocidad y espacio que definen el
movimiento de la superficie del líquido. ¿De qué movimiento se trata?
3. Calcula el tiempo que la bureta tardaría en descender 25 cm.
4. ¿De qué manera podrías construir un reloj con los materiales de que dispones?. ¿Cuál
sería entonces la unidad de tiempo?.
ESTUDIO DE UN MOVIMIENTO RECTILINEO Y UNIFORME (2)
Objetivo:
Obtener la relación entre el espacio y el tiempo para
un cuerpo que se mueve con velocidad constante,
pero esta vez utilizaremos un montaje un poco más
complejo y un cronovibrador para medir los tiempos.
Material:
Motor, vástago, correa de transmisión de goma para
unirlos y soportes.
Regla de deslizamiento, taco y cinta con papel
copiable e hilo.
Cronovibrador y fuente de alimentación.
Procedimiento:
El motor gira con velocidad uniforme y comunica su
movimiento a través del correillo de goma al vástago,
el cual gira uniformemente y va enrollando el hilo. El
hilo, a su vez, tira del taco mediante el papel
copiable.
Los tiempos se miden con un cronovibrador, que es
un aparato que funciona con corriente alterna de unos
40 voltios y vibra con la misma frecuencia de la
corriente: 50 Hercios. Eso quiere decir que sobre la
cinta de papel se marcarán 50 puntos cada segundo,
es decir, el intervalo entre una marca y las siguientes
de 0.02 segundos.
Al utilizar papel copiable, por cada golpe que dé el
cronovibrador se marcará un punto en la cinta de
papel
Las marcas sobre el papel tendrán un aspecto como el de la figura. Si los puntos están muy
juntos los tomaremos de 5 en 5, sin olvidar que en este caso los intervalos de tiempo serían 5
veces mayores, o sea 5*0,02=0.1 segundos.
Recogida de datos
Todos los valores los recogemos de forma ordenada en una tabla como la siguiente:
(s) espacio
recorrido
so
0 m
s1
s2
s3
s4
s5
s6
(t) tiempo
empleado
to
0 s
t1
0,1
t2
0,2
t3
0,3
t4
0,4
t5
0,5
t6
0,6
∆s
s1−so
s2−s1
s3−s2
s4−s3
s5−s4
s6−s5
∆t
m
t1−to
t2−t1
t3−t2
t4−t3
t5−t4
t6−t5
v = ∆s/∆t
0,1 s
0,1 s
0,1 s
0,1 s
0,1 s
0,1 s
Tratamiento de los datos obtenidos:
1. Representa gráficamente el espacio (s) en función del tiempo (t), pero antes observa los
datos que debes representar y en función de ellos elige el valor que darás a las divisiones de
los ejes.
2. Representa gráficamente la velocidad (v) en función del tiempo (t).
Velocidad en un punto Q.
Para calcular la velocidad en el punto Q por ejemplo, se toma como intervalo de espacios la
distancia comprendida entre el punto anterior y posterior a él, y como es natural el intervalo
de tiempo será el doble: 0,2 seg.
vQ =
s5 − s3
t5 − t3
Obviamente la velocidad, así calculada, es la velocidad media correspondiente a ese
intervalo. ¿Qué podríamos hacer para obtener un valor más cercano a la velocidad
instantánea en el punto Q?
ESTUDIO DE UN MOVIMIENTO RECTILINEO UNIFORMEMENTE ACELERADO.
Objetivo:
Vamos a estudiar el movimiento de una bola
que cae por un plano inclinado y vamos a
comprobar que se trata de un movimiento
uniformemente acelerado, es decir, que la bola
desliza con una aceleración constante.
Material
Carril de deslizamiento con taladros cada 50cm
Bola, Soporte y Cronómetro (pueden valer los
relojes digitales)
Procedimiento:
Prepara el montaje de la figura. Coloca un tornillo en el primer taladro del carril (50cm).
Deja caer la bola desde el extremo del carril (que será el cero del sistema de referencia) y
mide el tiempo que tarda en recorrer los primeros 50 cm, es decir, el tiempo desde que
sueltas la bola hasta que golpee en el tornillo.
Repite la operación colocando el tornillo a 1m, 1,5m, etc
Conviene que hagas 5 medidas del tiempo para cada distancia y tomes como buena el valor
medio. De esa forma el error que cometes será menor.
Recogida de datos
Todos los valores los recogemos de forma ordenada en una tabla como la siguiente:
(s) espacio
recorrido
so
0 m
s1
0,5 m
s2
1,0 m
s3
1,5 m
s4
2,0 m
s5
2,5 m
s6
3,0 m
(t) tiempo
empleado
to
0 s
t1
t2
t3
t4
t5
t6
(t2) tiempo
al cuadrado
0 s2
∆s
s1−so
s2−s1
s3−s2
s4−s3
s5−s4
s6−s5
0,5
0,5
0,5
0,5
0,5
0,5
Tratamiento de los datos obtenidos:
1. Representa la grafica del espacio en función del tiempo.
∆t
m
m
m
m
m
m
t1−to
t2−t1
t3−t2
t4−t3
t5−t4
t6−t5
v = ∆s/∆t
2. Representa la grafica del espacio en función del tiempo al cuadrado.
3. Representa la gráfica de la velocidad en función del tiempo empleado.
4. Junto a cada gráfica haz una interpretación de la misma y encuentra la relación
matemática que relaciona a las dos variables.
Cuestiones:
1, Cuales son las ecuaciones de la aceleración, velocidad y espacio que definen el
movimiento de la bola. ¿De qué movimiento se trata?
2, ¿Qué es la velocidad media? Calcula su valor.
3. ¿Influye la masa de la bola en la rapidez con la que alcanza las distintas marcas?
LEY DE HOOKE
Objetivo:
Encontrar la relación que existe entre la fuerza aplicada a un muelle (fuerza deformadora) y
la deformación que experimenta.
Como fuerza deformadora utilizaremos el peso ejercido sobre el resorte por un conjunto de
masas.
Material:
Soporte, nuez, pinzas y regla
Resorte, portapesas y diversas pesas de masa conocida o que puede medirse con la balanza.
Procedimiento:
Realiza un montaje como el de la figura. No coloques la regla a cero hasta haber colgado el
portapesas porque, de esta forma, a la distancia que se deforme al colgar una masa no habrá
que restarle la deformación debida al peso del portapesas. (sería como cambiar el origen del
sistema de referencia y ponerlo en el lugar más cómodo para nosotros).
Ahora coloca distintas pesas de masa conocida sobre el portapesas y anota en el cuadro el
valor de las masas y la deformación que el resorte experimenta para cada una de ellas.
(Procura no sobrepasar los 100 gramos de masa aproximadamente, porque si colocas masas
muy grandes provocarás una deformación permanente en el muelle.)
Recogida de datos:
Todos los valores los recogemos de forma ordenada en una tabla como la siguiente:
Masa colgada (gramos)
0g
20 g
Fdeformadora = Peso (Newton)
0N
x = Deformación (metros)
0m
100 g
Tratamiento de los datos obtenidos:
1. Representa gráficamente la fuerza deformadora ejercida en función de la deformación
provocada
2. Encuentra la relación matemática que relaciona a las dos variables. Ley de Hooke.
Cuestiones:
1. Enuncia la ley de Hooke
2. ¿Podrías utilizar tu muelle para pesar pequeños objetos?