MECANICA APLICADA II. EXAMEN FINAL. 10-2

MECANICA APLICADA II. EXAMEN FINAL. 10-2-97.
PRIMER EJERCICIO. TIEMPO: 40'
Elegir sólo 2 de las 3 preguntas:
1. Teoremas de Köenig.
2. Aplicación del teorema del momento cinético al centro instantáneo de rotación.
3. Deducción de las ecuaciones de Euler.
MECANICA APLICADA II. EXAMEN FINAL. 10-2-97.
SEGUNDO EJERCICIO. TIEMPO: 45'
Un disco de masa M y radio R está sometido a la acción de un par motor Pm y apoyado
sobre un suelo horizontal rugoso, de modo que el máximo par que puede actuar sobre el
disco sin que éste deslice vale MgR.
Al tiempo que el par motor deja de actuar se inclina dicho suelo rugoso. Calcular la
máxima inclinación posible para que el disco siga sin deslizar.
Pm
Mg
Mg
ϕ
MECANICA APLICADA II. EXAMEN FINAL. 10-2-97.
TERCER EJERCICIO. TIEMPO: 45'
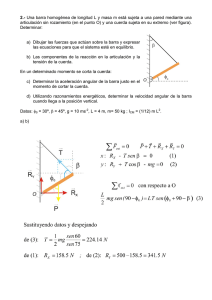
Una placa triangular de masa M y espesor despreciable está soldada a un eje vertical, en
el mismo plano vertical y también soldado a ese eje se sitúa un semiaro de masa M y
radio R tal y como se indica en la figura. El sistema gira con velocidad angular ω
constante alrededor de ese eje. Se pide calcular:
1. Tensor axil en O.(3 puntos)
2. Reacciones en los apoyos.(4 puntos)
3. Equilibrar el sistema con una masa a una distancia R del eje.(3 puntos)
A
R
R
O
R
R
R
B
MECANICA APLICADA II. EXAMEN FINAL. 10-2-97.
CUARTO EJERCICIO. TIEMPO: 50'
El sólido rígido de la figura está formado por dos discos de radio R y R/2 y masa M y
m, cuyos centros están unidos por medio de una barra sin masa ortogonal a los discos.
El sólido rígido está dotado de un movimiento de rodadura pura (existe rozamiento
suficiente) sobre un plano horizontal de forma que la intersección de la prolongación de
la barra con el plano horizontal permanece fijo. La velocidad angular de precesión ω es
constante.
Se pide:
a.- Valor de la resultante de las fuerzas normales para cualquier valor de ω.(1 punto)
b.- Valor de la velocidad de precesión máxima para que el sólido rígido no vuelque (en
la posición límite la resultante de las fuerzas de enlace normales al plano se encuentra
en el extremo A).(8 puntos)
c.- Para ω = 0 (reposo), relación entre m y M para que el sólido rígido no vuelque (la
resultante de las fuerzas normales se aplica en esta ocasión en B).(1 punto)
R
R/2
ω
ω
Mg
A
NA
B
NB
mg
30º
NA
NB
MECANICA APLICADA II. EXAMEN FINAL. 10-2-97.
QUINTO EJERCICIO. TIEMPO: 50'
El sistema de la figura está constituido por un bloque de masa M, apoyado sobre un
plano horizontal sin rozamiento, una barra OC de longitud L y masa M articulada en O
al bloque, y cuatro resortes iguales de constante K y longitud natural a. Determinar:
1) Valor de K para que el sistema se encuentre en equilibrio estable cuando la barra está
vertical (4 puntos).
2) Frecuencias de las pequeñas oscilaciones del sistema alrededor de la posición de
equilibrio estable para los siguientes valores particulares (6 puntos):
K=
3Mg
L
a=
L 2
3
C
L
A
L
L
O L
B
L
MECANICA APLICADA II. EXAMEN FINAL. 10-2-97.
SOLUCIONES
2º
3º
tgθ = 2
1)
2)
3)
4º
a)
b)
c)
5º
1)
2)
⎡4
⎤
0
0 ⎥
⎢3
⎢
2
1⎥
[ Io ] = ⎢ 0 3 − 12 ⎥MR2
⎢
1
2 ⎥
⎢0 −
⎥
⎣
12
3 ⎦
⎧ A x = Bx = 0
⎪ B = 2 Mg
⎪ z
⎪
⎛ 2 1 ⎞⎤
1 ⎡ MR 2 Mg Mg
⎨ By = ⎢
−
+ MRω2 ⎜ − ⎟⎥
ω +
⎝ π 3 ⎠⎦
2 ⎣ 24
6
π
⎪
⎪
MRω2 ⎛ 2 1 ⎞ 1 ⎡ MR 2 Mg Mg ⎤
⎜ − ⎟−
−
ω +
⎪A y =
2 ⎝ π 3 ⎠ 2 ⎢⎣ 24
6
π ⎥⎦
⎩
⎧
⎛ 2 1⎞
⎪ m = M⎜⎝ − ⎟⎠
π 3
⎪
⎪xm = 0
⎨
⎪ym = R
⎪
Rπ
⎪ zm = − (
4 6 − π)
⎩
N A + N B = ( M + m) g
16 3 ⎛ 2 M + 5m ⎞
⎜
⎟
ω2 =
57 ⎝ 4 M + m ⎠
M 1
=
m 2
Mg
K>
a 2
⎧ 2 6g
⎪ω1 = 5 L
⎨
⎪ω2 = 6 g
⎩ 2
L
MECANICA APLICADA II. EXAMEN FINAL. 3-9-97.
PRIMER EJERCICIO. TIEMPO 40’
Elegir sólo 2 de las 3 preguntas:
1. Tensor axil de inercia.
2. Ángulos de Euler.
3. Formas reducidas de la energía potencial y cinética.
MECANICA APLICADA II. EXAMEN FINAL. 3-9-97.
SEGUNDO EJERCICIO. TIEMPO 40’
El sistema de la figura está constituido por una barra homogénea BD de longitud
2L y masa 2M, y por la barra homogénea AC de masa M y longitud L 2 que se apoya
sobre la primera a través de la deslizadera articulada C, la cual desliza sin rozamiento a
lo largo de BD.
Ambas están situadas en un plano vertical y en el instante inicial, representado
en la figura, el sistema se encuentra en reposo. Si se deja que el sistema se mueva
libremente, determinar en dicho instante inicial (inmediatamente antes de que se inicie
el movimiento):
1.- Reacción existente en la deslizadera C. (4 puntos)
2.- Aceleración angular de la barra BD. (3 puntos)
3.- Aceleración angular de la barra AC. (3 puntos)
A
M,L
2
L
B
C
2M,2L
D
MECANICA APLICADA II. EXAMEN FINAL. 3-9-97.
TERCER EJERCICIO. TIEMPO 50’
Un cuarto de disco de radio R, masa M y espesor despreciable está soldado al
eje vertical como se indica en la figura. El eje gira con velocidad angular ω = sen t .
Calcular:
1. Reacciones en los apoyos en la dirección del eje X y par aplicado. (6 puntos)
Si se usan tres barras iguales, soldadas a 45º con la vertical como se indica en la figura,
para equilibrar el sistema. Determinar:
2. La masa m y la longitud L de las barras. (4 puntos)
A
3R/2
ω=sen t
mL
mL
Z
45º
45º
O
X
Y
45º
MR
3R/2
mL
B
MECANICA APLICADA II. EXAMEN FINAL. 3-9-97.
CUARTO EJERCICIO. TIEMPO 45’
Sean cuatro esferas iguales de masa M y radio R unidas mediante dos barras
perpendiculares sin masa tal y como se indica en la figura. La distancia desde el centro
de cualquier esfera al punto O de intersección de las barras es a. El punto O es un punto
fijo (hay una rotula esférica).
Sabiendo en el instante inicial,
la componente en la dirección del eje z (eje perpendicular al plano formado por las dos
barras) de la velocidad angular, ω oz y el ángulo de nutación θo ,
se pide:
obtener la expresión de la rotación propia y de la precesión en cualquier instante (en
función de M, R, a, ω oz y θo ).
→
Ho
z
O
MECANICA APLICADA II. EXAMEN FINAL. 3-9-97.
QUINTO EJERCICIO. TIEMPO 45’
El sistema de la figura está constituido por un resorte vertical de constante K y
longitud natural l0, y dos barras iguales OA y BC, de masa M y longitud L, articuladas
en el punto fijo O y en el punto medio de la barra OA, respectivamente. Sabiendo que
en la posición de equilibrio estable la barra OA está horizontal y la BC vertical,
calcular:
1. Deformación del resorte en el posición de equilibrio (1 punto).
2. Energía potencial reducida del sistema (3 puntos).
3. Energía cinética reducida del sistema (3 puntos).
4. Frecuencias de las pequeñas oscilaciones del sistema alrededor de la posición de
equilibrio estable (3 puntos).
O
K,l0
B
A
C
MECANICA APLICADA II. EXAMEN FINAL. 3-9-97.
SOLUCIONES
2.
2.1
Cy = 0
2.2
α BD = −
→
2.3
3.
3.1
3.2
4.
3g →
k
4L
→
3g →
k
α AC = −
4L
MR 2
P=
cos t
4
MR
Ax =
cos t
2π
5MR
Bx =
cos t
6π
R9 2
L=
16
M 128
m=
27π
⎛ 8 MR 2 + 4Ma 2 ⎞ ⋅ ω
⎜
⎟ oz
⋅
⎝5
⎠
ψo =
⎛ 8 MR 2 + 2 Ma 2 ⎞ ⋅ cos θ
⎜
⎟
o
⎝5
⎠
⎛ 8 MR 2 + 4Ma 2 ⎞ ⋅ ω
⎜
⎟ oz
⎝
⎠
= ω oz − 5
⎛ 8 MR 2 + 2 Ma 2 ⎞
⎜
⎟
⎝5
⎠
Mg
d = Lo +
K
2
2
1
1
L
V = KL2 ⋅ α + ⎛⎜ Mg ⎞⎟ ⋅ θ
2
2⎝
2⎠
⋅2
⋅2 1 1
1 7
T = ⎛⎜ ML2 ⎞⎟ ⋅ α + ⎛⎜ ML2 ⎞⎟ ⋅ θ
⎠
⎠
2 ⎝ 12
2⎝3
12K 2 3g
;ω =
ω2 =
7M
2L
⋅
ϕo
5.
5.1
5.2
5.3
5.4
( )
MECANICA APLICADA II. EXAMEN FINAL. 30-1-98.
PRIMER EJERCICIO. TIEMPO: 40'
Elegir sólo 2 de las 3 preguntas:
1. Teoremas de Steiner.
2. Cálculo del momento cinético de un sólido con punto fijo.
3. Giroscopio simétrico con movimiento por inercia. (Giroscopio de Euler)
MECANICA APLICADA II. EXAMEN FINAL. 30-1-98.
SEGUNDO EJERCICIO. TIEMPO: 50'
En la figura, el plano vertical π gira con velocidad angular constante ω. Una
barra OA también sin masa y de longitud L se mueve sobre el plano articulada en O al
eje. Un muelle ideal de constante elástica K=Mω2 une el extremo A a una masa puntual
M que desliza sobre la barra OA, sin rozamiento.
En el instante inicial t=0:
- la masa M se encuentra a una distancia L/2 de A sin velocidad relativa a la barra OA;
- barra y eje son perpendiculares entre sí siendo ω el valor de la velocidad angular
relativa entre la barra y el plano en el sentido indicado en la figura.
Determinar:
1. Ecuaciones diferenciales del movimiento de la masa M. (5 puntos)
2. Aceleración de la masa M relativa a la barra OA en el instante inicial. (1 punto)
3. Aceleración absoluta de la masa M en el instante inicial. (3 puntos)
4. Fuerzas de enlace entre masa M y barra OA en el instante inicial. (1 punto)
O
M
L
Mg
ω
A
MECANICA APLICADA II. EXAMEN FINAL. 30-1-98.
TERCER EJERCICIO. TIEMPO: 40'
Una barra AB de masa M y longitud 4R está suspendida en un plano vertical mediante
Mg
un hilo BC y un muelle ideal OA de constante K =
que forma 45º con la vertical.
2R
Sobre el punto medio de la barra se apoya un disco de masa M y radio R, no existiendo
rozamiento entre ambos.
Estando el sistema en equilibrio con la barra AB horizontal, se corta el hilo BC.
Determinar en dicho instante (inmediatamente antes de que se inicie el movimiento):
1. Aceleración del punto medio de la barra (2 puntos).
2. Aceleración angular de la barra (2 puntos).
3. Aceleración del centro del disco (2 puntos).
4. Aceleración angular del disco (2 puntos).
5. Reacción entre disco y barra (2 puntos).
O
C
D
45º
B
A
2R
4R
MECANICA APLICADA II. EXAMEN FINAL. 30-1-98.
CUARTO EJERCICIO. TIEMPO: 45'
Un sistema plano, formado por un cuadrado CDEF de masa M, lado 2L y
espesor despreciable, y por una barra CH de masa 2M y longitud 2L; gira alrededor del
eje AB vertical y fijo. Sabiendo que el apoyo A no admite esfuerzos axiales, determinar
g
g
y la aceleración angular α = :
en el instante en que la velocidad angular es ω =
L
L
1. Reacciones en los apoyos A y B y valor del par P necesario.
2. Posición en la que ha de colocarse una masa puntual M para equilibrar el sistema.
A
L
L
L
H
C
2Mg
D
L
ω,α
L
Mg
F
P
B
E
L
MECANICA APLICADA II. EXAMEN FINAL. 30-1-98.
QUINTO EJERCICIO. TIEMPO: 45'
El sistema de la figura está compuesto por una barra OA de masa M y longitud
3 2
R , y por un disco de centro C, masa M y radio R. La barra OA está articulada en
4
O al techo y en A al disco. La distancia entre el punto de articulación del disco A y su
R
.
centro C es
2
Sabiendo que la posición de equilibrio estable es la de la figura, determinar:
1) Energía potencial reducida del sistema.
2) Energía cinética reducida del sistema.
3) Frecuencias de las pequeñas oscilaciones del sistema alrededor de la posición de
equilibrio estable.
O
M,
3 2
R
4
A
R
2
C
M, R
MECANICA APLICADA II. EXAMEN FINAL. 30-1-98.
SOLUCIONES
2.
[
]
2.1
&x& + ω 2 cos 2 θ (L − x ) + θ& 2 (L − x ) + g sen θ + ω 2 x = 0
θ&&(L − x )2 − 2 x&θ&(L − x ) + ω 2 (L − x )2 sen θ cos θ − g cos θ (L − x ) = 0
2.2
a MrelAB =
2.3
aM =
2.4
F=0
3.1
a GdeAB = − g i −
3.2
α AB = −
3.3
a GdeDisco
3.4
α Disco = 0 k
3.5
N=
→
→
→
3L 2 →
ω j
2
→
L 2→
ω j− g k
2
→
→
3.
→
→
→
→
4.
g→
j
2
3g →
k
2R
g→
=− j
2
→
→
Mg →
j
2
→
→
5
Mg j
4
4.1
→
A = Mg i +
→
→
→
1
B = − Mg j + 3Mg k
4
(0 L L )
4.2
5.
5.1
5.2
5.3
⎞ 2 1⎛ 1
1⎛9 2
⎞ 2
⎜
⎟θ + ⎜
MgR
MgR
⎟ϕ
⎟
2 ⎜⎝ 8
2
2
⎝
⎠
⎠
3
1
3
Tred = (MR 2 )θ& 2 + (MR 2 )ϕ& 2 + (MR 2 )θ&ϕ&
4
2
4
10 ± 2 g
ω2 =
5 R
V red =
MECANICA APLICADA II. EXAMEN FINAL. 3-9-98.
PRIMER EJERCICIO. TIEMPO: 40'
Elegir sólo 2 de las 3 preguntas:
1. Tensor axil de inercia.
2. Teorema de Köenig de la energía.
3. Angulos de Euler.
MECANICA APLICADA II. EXAMEN FINAL. 3-9-98.
SEGUNDO EJERCICIO. TIEMPO: 50'
Una barra OA de masa M y longitud
2 L está suspendida en un plano vertical
mediante un hilo h en el extremo A y una articulación a una pared en el extremo O. En
2M
el extremo A se articula otra barra AB de longitud L y masa
libre en el extremo B.
3
Estando el sistema en equilibrio con la barra OA a 45º y la barra AB vertical calcular:
1. Reacciones en la articulación O y fuerza en el hilo h (2 puntos).
Si ahora se corta el hilo h. Determinar en dicho instante (inmediatamente antes de que
se inicie el movimiento):
2. Aceleración angular de las barras (4 puntos).
3. Reacciones en las articulaciones (4 puntos).
h
A
2L
M
L
2M
3
45º
O
B
MECANICA APLICADA II. EXAMEN FINAL. 3-9-98.
TERCER EJERCICIO. TIEMPO: 50'
Dos cuadrados iguales de masa M, lado L y espesor despreciable están situados en
planos perpendiculares verticales y giran alrededor del eje vertical AD con velocidad
2g
2g
sen
t por la acción de un par desconocido P. Sabiendo que el
angular ω =
L
L
apoyo D no puede absorber esfuerzos verticales, se pide:
1. Valor del par P, en el instante t = 0 (2 puntos).
2. Calcular las reacciones en los apoyos A y D en el instante t = 0 (4 puntos).
3. Si se equilibra el sistema colocando dos masas iguales de valor M en los planos
perpendiculares al eje que pasan por B y C respectivamente, determinar su
posición en los planos (4 puntos).
Z
D
L
C
L
L
B
L
A
X
Y
MECANICA APLICADA II. EXAMEN FINAL. 3-9-98.
CUARTO EJERCICIO. TIEMPO: 45'
Un disco de masa M y radio R y espesor despreciable, cuyo centro O siempre
permanece fijo, gira en el instante inicial con velocidad angular ω o alrededor de un eje
que pasa por el punto O y forma 45º con el eje de revolución del disco como se indica
en la figura.
Calcular en el movimiento posterior los valores de:
1. Velocidad y ángulo de nutación.
2. Velocidad de precesión.
3. Velocidad de rotación propia.
45º
O
ωo
A
MECANICA APLICADA II. EXAMEN FINAL. 3-9-98.
QUINTO EJERCICIO. TIEMPO: 40'
El sistema mecánico de la figura está constituido por dos barras articuladas entre
sí: la barra OA de longitud L sin masa y la barra AB de masa M y longitud L. Las
barras pueden oscilar en el plano vertical del dibujo. Se pide determinar alrededor de la
posición de equilibrio estable:
1. La energía potencial reducida del sistema.(3 puntos)
2. La energía cinética reducida del sistema. (3 puntos)
3. La frecuencias naturales de oscilación del sistema. (4 puntos)
O
L
A
M,L
B
MECANICA APLICADA II. EXAMEN FINAL. 3-9-98.
SOLUCIONES
2.-
1.
2.
3.
3.-
1.
2.
3.
4.-
1.
2.
3.
5.-
1.
2.
3.
H o = 0 ; Vo =
Mg
;
2
T=
7Mg
6
7g
7g
; α AB = −
9L
6L
14Mg
41Mg
; Vo =
Ho =
27
54
7Mg
4Mg
;V A = −
HA =−
54
27
4MgL
P=
3
Mg
Mg
; Ay =
; Az = 2 Mg
Ax = −
2
2
Mg
Mg
; Dy =
Dx = −
2
2
L
3
L
L
⎛
⎞ ⎛ 3L
⎞
B⎜ −
−
L ⎟ ; C⎜ −
−
3L ⎟
8
8
⎝ 8
⎠ ⎝ 8
⎠
2
θ& = 0; cos θ =
5
5
ψ& = ω o
2
1
ϕ& = −ω o
2
1
1⎛
L⎞
V reducida = (MgL )θ 2 + ⎜ Mg ⎟ϕ 2
2
2⎝
2⎠
2
1
1 ⎛ ML ⎞ 2 ⎛ ML2
⎟ϕ& + ⎜⎜
Treducida = (ML2 )θ& 2 + ⎜⎜
2
2 ⎝ 3 ⎟⎠
⎝ 2
g
ω 2 = 5 ± 19
L
α OA = −
(
)
⎞ &
⎟⎟ϕ&θ
⎠
MECANICA APLICADA II. EXAMEN FINAL. 30-01-99.
PRIMER EJERCICIO TIEMPO: 40’
Responder a todas las preguntas:
Z
1. Calcular las coordenadas del centro de gravedad, y
el producto de inercia Cx de la figura utilizando las
L
integrales precisas. (2 puntos)
M
X
Y
L
2. En el sistema mecánico sin rozamiento de la figura
indicar:
Z
a) Ecuaciones de enlace.
b) Tipos de enlace.
M
c) Coordenadas generalizadas.
Ω cte
L
Y
d) Indicar
cómo
se
aplicaría
el
teorema de la energía para obtener
una ecuación del movimiento.
X
(2 puntos)
3. Demostrar que en un giróscopo de Euler-Poinsot simétrico (movimiento por inercia)
el movimiento es siempre estacionario. (3 puntos).
4. El sistema de la figura está constituido por una barra
O
OA sin masa de longitud L y una barra AB de masa M
L
y longitud L. Calcular el momento cinético del sistema
respecto de los puntos O, A, y G en la posición de la
θ
A
M,L
figura.(3 puntos)
ϕ
G
B
MECANICA APLICADA II. EXAMEN FINAL. 30-01-99.
SEGUNDO EJERCICIO TIEMPO: 40’
Una barra AB de masa M y longitud 3L soporta una masa puntual M, no existiendo
rozamiento entre ambas. El sistema está en equilibrio mediante el muelle ideal AC de
constante K y la barra rígida BD, observándose que ésta soporta un esfuerzo de
magnitud Mg.
Determinar:
1. El valor de la constante K en el equilibrio.(2 puntos)
2. La reacción entre la masa puntual y la barra AB en el instante subsiguiente al de
eliminar la barra BD. (8 puntos)
D
L
L/2
O
A
M
B
K
Lo=0
L
C
M, 3L
MECANICA APLICADA II. EXAMEN FINAL. 30-01-99.
TERCER EJERCICIO TIEMPO: 45’
Una placa triangular de masa M y espesor despreciable, está soldada a un eje vertical y
a una barra CD de masa M y longitud 2 2 L como se indica en la figura. Todo el
sistema está contenido en un plano vertical que gira con velocidad angular constante ω
alrededor del eje vertical. Se pide calcular:
1. Reacciones en los apoyos. (6 puntos)
2. Equilibrar el sistema con una masa de valor m=M/2, dando sus coordenadas.
(4 puntos)
B
D
L
z
ω
L
2L
45º
O
y
L
C
L
A
MECANICA APLICADA II. EXAMEN FINAL. 30-01-99.
CUARTO EJERCICIO TIEMPO: 45’
La barra OA, de masa M y longitud L, está rígidamente unida al disco de masa M y
radio L/4. El centro del disco, está unido a un muelle de constante elástica 4Mg/L y
longitud sin tensión L. Sobre la barra OA hay una deslizadera de masa M que está
unida a su vez a un muelle de constante elástica Mg/L y longitud sin tensión L cuyo
otro extremo se encuentra en el punto A de la barra. El disco rueda sin deslizar sobre un
suelo horizontal. Se pide:
1. Obtener la posición de equilibrio estable vertical. (3 puntos)
2. En esa posición obtener la energía cinética y potencial reducida. (4 puntos)
3. Calcular las frecuencias naturales del sistema. (3 puntos)
L
M
R= L/4
O
K´= 4Mg/L
Lo= L
M, L
M
K= Mg/L
Lo= L
A
MECANICA APLICADA II. EXAMEN FINAL. 30-01-99.
QUINTO EJERCICIO TIEMPO: 40’
El sistema de la figura está situado en el plano vertical y constituido por dos barras
iguales de masa M y longitud L articuladas en A y posicionadas como se indica en la
figura, un disco de masa M y radio R y un muelle de longitud sin tensión L0 y constante
K cuyos extremos están unidos al suelo y al punto medio E de la barra AB.
Se lanza el disco contra la barra AB y se produce un choque elástico y sin
rozamiento en el extremo B de dicha barra. En el instante anterior al choque, el disco
r
posee una velocidad angular conocida ω y la velocidad de su centro de gravedad es
vertical, conocida y de valor v.
Determinar, inmediatamente después del choque:
1. Energía cinética del sistema constituido por las barras, el muelle y el disco (1 punto).
2. Velocidad angular del disco (1 punto).
3. Velocidad angular de las barras OA y AB (8 puntos).
ω
45º
C
A
E
B
K,Lo
O
D
v
MECANICA APLICADA II. EXAMEN FINAL. 30-01-99.
SOLUCIONES
2.-
1.
2.
3.-
3Mg
L
9
N = Mg
5
K=
1.
Ax = 0
Mg 2
+ MLω 2
4
3
Az = 2 Mg
Ay = −
Bx = 0
By =
Mg 1
+ MLω 2
4
3
2.
4.-
⎧
⎪x = 0
⎪
⎨ y = 2L
⎪
2
⎪z = − L
3
⎩
1.
AM = 0
2.
Coordenadas generalizadas: θ giro del disco y x desplazamiento de la
deslizadera desde el extremo A.
⎤
⎡ 7 MgL
0 ⎥ ⎧θ ⎫
⎢ 4
1
V red = ⋅ {θ x}⎢
Mg ⎥ ⎨⎩ x ⎬⎭
2
0
⎥
⎢
L ⎦
⎣
⎡ 77 ML2
⎤ ⎧θ& ⎫
1 &
0
⎢
⎥⎨ ⎬
&
Tred = ⋅ θ x
2
⎢ 96
M ⎥⎦ ⎩ x& ⎭
⎣ 0
g
ω2 =
L
3.
24 g
ω2 =
11L
1
1 MR 2 2
1.
T = Mv 2 +
ω
2
2 2
{
5.-
→
2.
3.
→
Ω disco = −ω k
→
6v →
k
Ω barraOA =
23L
→
24v →
Ω barraAB = −
k
23L
}
MECANICA APLICADA II. EXAMEN FINAL. 09-09-99.
PRIMER EJERCICIO TIEMPO: 50’
1. Calcular el centro de gravedad de la figura así
Z
como el momento de inercia respecto del eje X
y el producto de inercia respecto de los planos
XOZ e YOZ. Densidad ρ = 4M
R
πR 2
R/4
O
X
(1 punto)
2. Ecuaciones de Euler.
45º
C
Y
OC=R/2
(2 puntos)
3. Cálculo del momento cinético de un sólido con punto fijo
4. Obtener el sistema de ecuaciones
diferenciales del movimiento absoluto
Lo=0
K
M
(2 puntos)
Lo=0
K
Lo=0
K
M
de las masas.
(2 puntos)
L
L
L
5. Una masa M se suelta a una altura H y rebota hasta H/2. No hay rozamiento.
Calcular el coeficiente de restitución de Newton. (1 punto)
6. Un disco de masa M y radio R desciende por un
plano inclinado de 30º partiendo del reposo.
M
Explicar en cuál de las situaciones siguientes el
disco llega al suelo con mayor velocidad de su
centro si en ambos casos parte de la misma altura:
a)
no existe rozamiento
b)
existe rozamiento suficiente para garantizar la
rodadura.
30º
(2 puntos)
MECANICA APLICADA II. EXAMEN FINAL. 09-09-99.
SEGUNDO EJERCICIO TIEMPO: 45’
Una circunferencia de alambre sin masa lleva soldada una masa puntual M. Se coloca
sobre un suelo rugoso de coeficiente de rozamiento f = 1
3
tal y como se indica en la
figura. Determinar:
1. Valor del ángulo α para que al dejarla libre no se produzca deslizamiento en el
contacto con el suelo. (3 puntos)
2. Reacción en el suelo en el primer instante. (7 puntos)
α
Mg
MECANICA APLICADA II. EXAMEN FINAL.09 -09-99.
TERCER EJERCICIO TIEMPO: 50‘
Una placa circular de masa 4M, radio 2R, y espesor despreciable, está soldada a un eje
horizontal. Se le practican tres agujeros circulares de radio R/2 y R tal y como se indica
en la figura. El sistema gira con velocidad angular Ω=sen(t). Se pide:
1. Equilibrar el sistema con una masa m a determinar situada en la línea de centros de
los agujeros. (8 puntos)
2. Reacciones en los apoyos del sistema una vez equilibrado. (2 puntos)
4R
4R
R/2
45º
Ω, α
e
2R
A
R
B
MECANICA APLICADA II. EXAMEN FINAL.09 -09-99.
CUARTO EJERCICIO TIEMPO: 50‘
Un disco de masa M, radio R y espesor despreciable está ligado a una rótula
esférica en O mediante una barra OG de longitud R, perpendicular a su plano y sin
masa.
En el instante inicial la barra OG está en posición vertical con β = 0 y el disco
gira a su alrededor con velocidad angular ω =
10g
, es decir, con rotación propia de
R
10g
y precesión y nutación nulas. Estando en esa posición el disco recibe una
R
percusión de módulo P = M 5gR , situada en el plano del disco y en la dirección de un
diámetro.
valor
Sabiendo que, debido a la percusión, la barra OG rota alrededor del punto O
ascendiendo y formando con la vertical un ángulo β , calcular:
1. Rotación β& de barra OG inmediatamente después de la percusión. (2 puntos)
2. Percusión de enlace en la rótula O. (2 puntos)
3. Valor del ángulo β cuando la barra llegue a su máximo ascenso. (6 puntos)
MECANICA APLICADA II. EXAMEN FINAL.09 -09-99.
CUARTO EJERCICIO TIEMPO: 50‘
O
O
β&
θ
β
P
G
G
ω
Posición inicial
ϕ&
Posición en un
instante cualquiera
MECANICA APLICADA II. EXAMEN FINAL.09 -09-99.
QUINTO EJERCICIO TIEMPO: 45‘
El semiaro ACB, de masa M y radio R, está soldado al diámetro AB, de masa
despreciable, cuyo punto medio O fijo es una articulación alrededor de la cual puede
girar el semiaro en un plano vertical. A lo largo del aro puede deslizar la barra DE, de
masa M y longitud
3R , mediante dos deslizaderas articuladas que se encuentran
unidas a O mediante 2 muelles de constante elástica K=Mg/R, y longitud sin tensión
Lo=2R. La posición indicada en la figura es de equilibrio estable.
Calcular la expresión de la energía potencial reducida (3 puntos) y la energía cinética
reducida (7 puntos).
O
A
B
E
D
C
MECANICA APLICADA II. EXAMEN PARCIAL. 9-9-99.
SOLUCIONES
2.
α = 60º
→
⎛ 3 → 3 →⎞
R = Mg⎜⎜
i + j ⎟⎟
4
4 ⎠
⎝
3.
m=
→
RA =
•
4.
β=
→
O=
69 Mg →
i
52
4
→
RB =
0 −
13 2 R ⎞
⎟
8 ⎟⎠
69 Mg →
i
52
g
R
5
M gR
β = 90º
5.
⎛ 13 2 R
⎜−
⎜
8
⎝
2
M
13
5
→
j
Siendo θ el ángulo de posición absoluta del semiaro, y ϕ el ángulo de posición
absoluta de la barra.
R⎤
2R ⎤ 2 1 ⎡
1⎡
Vred = ⎢ Mg
θ + ⎢ Mg ⎥ϕ 2
⎥
2⎦
2⎣
2⎣
π ⎦
1
1 ⎡ MR 2 ⎤ 2
Tred = MR 2 θ& 2 + ⎢
ϕ&
2
2 ⎣ 2 ⎥⎦
[
]
MECANICA APLICADA II. EXAMEN PARCIAL. 20-11-99.
PRIMER EJERCICIO. TIEMPO: 60’
1. Calcular la posición del centro de gravedad de un cono de masa M, radio de la base
R y altura H, mediante las integrales precisas. (1 punto)
2. Explicar, sin demostración, por qué no se conserva la energía mecánica en un
sistema sometido a enlaces reónomos y perfectos. (1 punto)
3.
ϕ
Una barra AB de masa M y longitud L, está en
equilibrio en posición vertical sobre un suelo horizontal
sin rozamiento. Se separa el punto A ligeramente de la
vertical sin velocidad y se inicia el movimiento.
Demostrar que su centro de gravedad describe una recta
vertical, mediante la aplicación de los teoremas
fundamentales de la dinámica. (2 puntos)
A
B
4.
La figura consta de un cilindro hueco cuya superficie
lateral tiene una masa de 2M, y dos tapas circulares de
masa M cada una de ellas. El radio de las tapas es R y la
altura del cilindro R. Calcular el momento de inercia de
la figura respecto a su centro de gravedad. (1 punto)
R
R
5. Demostrar el teorema de Köenig de la energía cinética. (2 puntos)
6.
El extremo A de una barra de masa M y longitud L
asciende con velocidad constante de módulo v a lo largo
de MN. Sabiendo que no existe rozamiento, calcular el
trabajo virtual realizado por:
1. Las fuerzas de enlace. (0,5 puntos)
2. Las fuerzas aplicadas. (0,5 puntos)
M
v
A
ϕ
Mg
B
N
7.
MgR
Mg
Calcular el valor de la fuerza de rozamiento entre disco
y suelo, si el coeficiente de fricción entre ambos es
f=1/2, cuando se aplica sobre el disco un par de valor
MgR. (2 puntos)
MECANICA APLICADA II. EXAMEN PARCIAL. 20-11-99.
SEGUNDO EJERCICIO. TIEMPO: 50’
El sistema de la figura consta de 2 barras iguales OA y AB, de masa M y longitud L,
unidas entre sí en el punto A y a un eje vertical en el punto O mediante articulaciones
planas. El punto B puede deslizar sin rozamiento a lo largo del eje a través de una
deslizadera articulada. A su vez, el punto A está unido al eje a través de un muelle ideal
12 Mg
AC, de constante elástica K =
. En el extremo C, el muelle presenta una
L
deslizadera articulada sin masa que puede moverse sin rozamiento a lo largo del eje. El
eje gira con velocidad angular constante ω. Determinar el valor de ω para que el ángulo
θ sea permanentemente de 60 º.
O
θ
C
B
A
MECANICA APLICADA II. EXAMEN PARCIAL. 20-11-99.
TERCER EJERCICIO. TIEMPO: 50’
El sistema plano de la figura consta de dos barras iguales de masa M y longitud 2R
articuladas en sus extremos y un disco de masa M y radio R, apoyado sobre un suelo
rugoso que garantiza la rodadura. Sabiendo que parte del reposo en la posición indicada
(AB vertical, BC horizontal y C a la misma altura que O), calcular en el instante
subsiguiente:
1. Aceleración angular de AB, de BC y del disco. (6 puntos)
2. Valor mínimo del coeficiente de rozamiento para asegurar la rodadura. (4 puntos)
A
C
B
O
MECANICA APLICADA II. EXAMEN PARCIAL. 15-01-2000.
PRIMER EJERCICIO. TIEMPO: 60’
1.
2R
O
2.
G
2R
Un disco de masa M y radio R, que está unido a una
barra OG sin masa, rueda sobre un plano horizontal de
modo que su centro G describe una circunferencia de
radio 2R con velocidad de módulo constante V.
Calcular el valor del momento giroscópico, es decir, el
momento de las fuerzas de inercia respecto del punto
fijo O.
(2 puntos)
a) Deducir las ecuaciones de Euler. (1 punto)
b) Mediante el empleo de las ecuaciones de Euler, obtener el par a aplicar al sólido
de la figura para que gire con ω constante. (1 punto)
ω
3. Deducir la forma reducida de la energía potencial para las pequeñas oscilaciones de
un sistema alrededor de la posición de equilibrio estable. (2 puntos)
4.
O
a
60º
M,L
Una barra de masa M y longitud L, articulada en O a un
punto fijo, se abandona a la acción gravitatoria en la
posición de la figura. Si se coloca un tope en la vertical
a una distancia a del punto fijo y el choque que se
produce es perfectamente elástico y sin rozamiento,
• ¿Cuál es ángulo máximo que alcanza? (1 punto).
• Si el tope se coloca a otra altura, ¿varía ese
ángulo?, ¿por qué? (1 punto).
5.
Z
Y
Equilibrar mediante una masa puntual M el sistema de
la figura de masa M, radio exterior R e interior R/2.
(2 puntos)
MECANICA APLICADA II. EXAMEN PARCIAL. 15-01-2000.
SEGUNDO EJERCICIO. TIEMPO: 50’
Sea el giróscopo de la figura constituido por un disco de masa M y radio R y una masa
puntual M que están unidos mediante una barra sin masa y de longitud 2R. El punto
medio de la barra está ligado mediante una articulación esférica y el giróscopo gira con
una velocidad angular ωalrededor de su eje de revolución, permaneciendo la barra
horizontal.
Un bloque de masa M/2 y dimensiones despreciables choca con la masa puntual. Justo
antes del choque, el bloque tiene una velocidad vertical ascendente de valor v = 5ωR .
El choque es sin rozamiento (la percusión tiene la dirección vertical) y se observa que
inmediatamente después del choque la velocidad vertical del bloque es nula.
Se pide para el instante inmediatamente después de la percusión:
1.- Velocidad angular del giróscopo.
2.- Coeficiente de restitución del choque.
3.- Velocidad de precesión, rotación propia y ángulo de nutación.
4.- Aceleración angular del giróscopo.
(2 puntos)
(2 puntos)
(4 puntos)
(2 puntos)
ω
v
MECANICA APLICADA II. EXAMEN PARCIAL. 15-01-2000.
TERCER EJERCICIO. TIEMPO: 50’
Un disco de masa M y radio R puede girar alrededor de su centro fijo O. Por su
periferia, y sin deslizar sobre el disco, pasa una cuerda atada en uno de sus extremos a
Mg
un muelle ideal de constante
, y a una masa puntual M en el otro extremo que
R
puede oscilar en torno a la posición vertical. Sabiendo que la longitud total del cable es
(4 + π )R y que la posición de la figura es de equilibrio estable, determinar:
1. Expresión de la energía potencial en una posición cualquiera. (3 puntos)
2. Deformación del muelle en la posición de equilibrio estable. (1 punto)
3. Frecuencia de las pequeñas oscilaciones alrededor de esa posición. (6 puntos)
O R
3R
M
Mg/R
MECANICA APLICADA II. EXAMENES PARCIALES. 1999-2000.
SOLUCIONES
MECANICA APLICADA II. EXAMEN FINAL. 26-01-2000.
PRIMER EJERCICIO. TIEMPO: 50’
Desarrollar las siguientes tres preguntas:
1. Dinámica de sólido rígido: Cálculo de la energía cinética de un sólido rígido con un
punto fijo (3 puntos).
2. Dinámica del sólido con eje fijo: Equilibrado de rotores (4 puntos).
3. Dinámica de Percusiones: Teorema de Carnot (3 puntos).
MECANICA APLICADA II. EXAMEN FINAL. 26-01-2000.
SEGUNDO EJERCICIO. TIEMPO: 50’
Un disco D1 de masa M y radio R está situado sobre una rampa fija inclinada 45º de
modo que entre ambos existe rozamiento suficiente para asegurar la rodadura. Su centro
está unido mediante una cuerda a otro disco D2 de masa M/2 y radio R/2, de modo que
la cuerda está arrollada a la periferia de este último como se indica en la figura. El disco
D2 se apoya en otra rampa fija de modo que no existe rozamiento entre ambos. En el
instante inicial el sistema está en reposo, y los centros de los discos situados a la misma
altura sobre el suelo. Calcular:
1. Posición del centro del disco D1 cuando el centro del disco D2 haya descendido en
vertical una distancia 2R (3 puntos).
2. Aceleración del centro de cada disco en ese instante. (4 puntos)
3. Tensión de la cuerda en ese instante. (3 puntos)
D1
D2
M, R
M/2
R/2
45º
45º
MECANICA APLICADA II. EXAMEN FINAL. 26-01-2000.
TERCER EJERCICIO. TIEMPO: 50’
Una barra OA de masa despreciable está soldada a un eje vertical e. Un disco de masa
M y radio R está articulado en A a la barra anterior pudiendo moverse en el plano
vertical que contiene al eje e y a ambos sólidos. Sabiendo que el conjunto gira alrededor
del eje e por la acción de un par P, determinar:
1. Energía cinética del disco (3 puntos).
2. Ecuaciones diferenciales del movimiento del disco (4 puntos).
3. Valor del par para que el conjunto gire a ω constante alrededor del eje e (3 puntos).
e
O
2R
A
R/2
C
P
MECANICA APLICADA II. EXAMEN FINAL. 26-01-2000.
CUARTO EJERCICIO. TIEMPO: 60’
El sólido de la figura está formado por un disco de masa M y radio R cuyo centro es
una rótula esférica fija, una barra sin masa OA de longitud R/2 perpendicular al plano
del disco, y una masa puntual M en el punto A. El sólido se abandona a la acción
gravitatoria partiendo de la posición de la figura existiendo en ese instante una rotación
alrededor de la línea OA de valor ω =
3g
.
2R
1. Comprobar que la otra posición en que la velocidad angular de nutación es nula
(valor absidal) es θ=120º, y obtener la velocidad angular de precesión y rotación propia
(5 puntos).
2. Si en ese instante se elimina la masa puntual sin modificar el campo de velocidades,
obtener los nuevos valores del ángulo de nutación, velocidad angular de precesión y
rotación propia (5 puntos).
A
60º
M
R/2
O
M,R
MECANICA APLICADA II. EXAMEN FINAL. 26-01-2000.
QUINTO EJERCICIO. TIEMPO: 45’
Una barra AB de masa M y longitud 2R está articulada a un punto fijo en A y en B al
centro de un disco de masa M y radio R. El conjunto formado por la barra y el disco se
abandona a la acción gravitatoria partiendo del reposo en la posición horizontal (línea
de puntos en la figura). Cuando la barra AB está en posición vertical, el disco golpea en
su punto medio E a la barra CD de longitud 2R y masa M, que se encuentra en reposo
articulada en C y unida a dos resortes horizontales en E y en D, ambos de la misma
constante elástica K y longitud natural 3L y cero, respectivamente.
Sabiendo que no existe rozamiento y que el choque es perfectamente elástico,
calcular:
1. Velocidad del punto B inmediatamente antes del choque. (2 puntos)
2. Percusión de enlace en el extremo D. (1 puntos)
3. Campo de velocidades del sistema inmediatamente después del choque. (7 puntos)
A
C
K,3L
E
B
K,0
D
L
Nota sobre el criterio de corrección: es necesario responder correctamente a las dos
primeras preguntas para aprobar el ejercicio.
MECANICA APLICADA II. EXAMEN FINAL. 26-01-2000.
SOLUCIONES
2. A) El disco D1 ha descendido 2R en vertical.
→
→
2 ⎛ 2 ⎛→ →⎞⎞
2 ⎛ 2 ⎛ → →⎞⎞
⎜⎜
⎜
B) a G1 = g
aG2 = g
⎜ i − j ⎟ ⎟⎟
⎜ − i − j ⎟ ⎟⎟
4 ⎝ 2 ⎝
4 ⎜⎝ 2 ⎝
⎠⎠
⎠⎠
2
8
C) T = Mg
⋅
⎡17
sen 2 θ ⎤ 3
2
2
3. A) T = MR ϕ ⎢ + sen θ +
+
MR
θ
⎥
8 ⎦ 8
⎣8
R
3 ⋅⋅ ⋅ ⎡
sen 2θ ⎤
= − Mg sen θ
B) θ − ϕ 2 ⎢cos θ +
⎥
4
8 ⎦
2
⎣
⋅
2
2
⋅
⎡ ⋅⋅
⎤
2
⋅ ⎡ ⋅
⎛
⎞
θ
θ
17
sen
sen 2θ ⎤⎥ ⎥
⎟⎟ + ϕ ⎢2 θ cos θ +
MR ⎢ϕ ⎜⎜ + 2 sen θ +
=P
⎢ ⎝4
4 ⎠
4 ⎥⎥
⎢
⎣
⎦⎦
⎣
⋅
⎡ ⋅
θ sen 2θ ⎤⎥
C) P = MR 2ω ⎢2 θ cos θ +
4 ⎥
⎢
⎣
⎦
2
⋅
4.
A)
B)
→
5.
A)
⋅
5 3g
3 2R
⋅
3g
ϕ =−
2R
4 3g
3 2R
⋅
4 3g
ψ=
3 2R
ϕ=
VB = −
3
2
ψ=
θ = 30º
→
gR i
PD = 0
B)
Nota sobre el criterio de corrección: es necesario responder correctamente a
las dos primeras preguntas para aprobar el ejercicio.
C)
→
→
→
→
→
→
VA = 0
VC = 0
VB = 0
→
→
Ω AB = 0
→
Ω CD = −
→
→
Ω disco = 0
3
2
g →
k
R
MECANICA APLICADA II. EXAMEN FINAL. 8-09-2000.
PRIMER EJERCICIO, TIEMPO: 50’
1. Aplicación del Teorema del momento cinético al centro instantáneo de rotación.
(3 puntos)
2. Teoremas fundamentales de la Dinámica de Percusiones.
(3 puntos)
3. Tensor Axil de Inercia.
(4 puntos)
MECANICA APLICADA II. EXAMEN FINAL. 8-09-2000.
SEGUNDO EJERCICIO, TIEMPO: 45’
El sistema de la figura está constituido por dos barras: barra AB de longitud L y masa
M, y barra CD de longitud 2L y masa despreciable. Los puntos A y C están situados a
la misma altura y el conjunto puede moverse libremente en un plano vertical.
Sabiendo que no existe rozamiento y que el sistema parte del reposo con las barras
horizontales, calcular para la posición de la figura:
1. Velocidad angular de la barra CD.
(4 puntos)
2. Aceleración angular de la barra CD.
(6 puntos)
A
C
L 3
30º
30º
M, L
L
D
B
L
MECANICA APLICADA II. EXAMEN FINAL. 8-09-2000.
TERCER EJERCICIO, TIEMPO: 50’
Dos discos iguales de radio R, masa M y espesor despreciable están situados en planos
perpendiculares y giran alrededor del eje vertical AD con velocidad angular de valor
ω=
⎛ g ⎞
g
sen⎜⎜
t ⎟⎟ por la acción de un par desconocido P. Sabiendo que el apoyo D
R
R
⎝
⎠
no puede absorver esfuerzos verticales se pide:
1. Valor del par P, en el instante t=0.
(2 puntos)
2. Reacciones en los apoyos en el instante t=0.
(3 puntos)
3. Si se equilibra el sistema colocando dos masas iguales de valor M en los planos
perpendiculares al eje pasando por B y C respectivamente, determinar su posición
en los planos.
(5 puntos)
Z
D
2R
C
2R
2R
B
2R
A
X
Y
MECANICA APLICADA II. EXAMEN FINAL. 8-09-2000.
CUARTO EJERCICIO, TIEMPO: 40’
El sistema de la figura consta de un aro homogéneo de masa M y radio R, que puede
rodar sin deslizar por un suelo horizontal. Dicho aro está atravesado por un diámetro sin
masa, por el cual puede deslizar sin rozamiento una masa puntual de valor M, unida a
los extremos de dicho diámetro mediante dos muelles iguales de constante elástica
K=
Mg
y longitud sin tensión R. El aro está unido mediante arandelas sin masa que
R
pueden deslizar sin rozamiento, a dos resortes iguales ideales de constante elástica
K=
Mg
. La posición de la figura es de equilibrio estable.
R
Calcular:
1. Energía potencial reducida del sistema.
(4 puntos)
2. Energía cinética reducida.
(6 puntos)
M, R
K=Mg/R
Lo=R
R
R
R
K=Mg/R
Lo=0
R/2
M
K=Mg/R
Lo=R
K=Mg/R
Lo=0
MECANICA APLICADA II. EXAMEN FINAL. 8-09-2000.
QUINTO EJERCICIO, TIEMPO: 35’
El sistema mecánico de la figura está formado por el sólido 1, barra de masa M y
longitud L articulada en un punto fijo O, y el sólido 2, barra de masa 2M/3 y longitud L
articulada en su punto medio al extremo de la barra 1.
Si se halla en reposo en la posición de la figura y se produce un choque perfectamente
elástico y sin rozamiento con una masa puntual M que se desplaza en dirección
horizontal a la altura del punto A con una velocidad constante de valor V = 2gL tal y
como se indica en la figura, calcular y dibujar la posición de cada uno de los elementos
del sistema mecánico en el máximo ascenso obtenido tras el choque.
O
M, L
1
V
3
A
2
2M/3, L
B
M
MECANICA APLICADA II. EXAMEN FINAL. 8-09-2000.
SOLUCIONES
2. 1.
2.