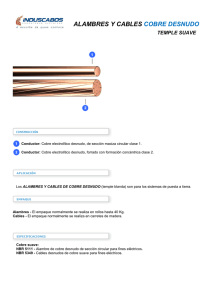
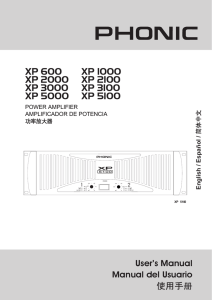
tendrán obligatoriamente la forma , con
Anuncio

SOLUCIONARIO ETAPA FINAL MATEMÁTICAS DIVERSIFICADO 1. Hallar la suma: 2008 2008 2008 2008 1 2 3 ... 2009 0 1 2 2008 Solución: n n . Por tanto: k nk Recuerde que 2008 2008 2008 2008 S 1 2 3 ... 2009 0 1 2 2008 2008 2008 2008 2008 2S 1 2 3 ... 2009 0 1 2 2008 2008 2008 2008 2008 2009 2008 2007 ... 1 0 1 2 2008 2008 2008 2008 2008 2S 2010 2010 2010 ... 2010 0 1 2 2008 2008 2008 2008 2008 2S 2010 ... 2008 0 1 2 Aplicando el binomio de Newton (1+1)2008, se obtiene 2S 2010 22008 S 2010 22007 2. Encuentre todos los números reales x y y tales que satisfagan el sistema de ecuaciones: x3 8 y 3 x 2 y 2x2 4xy 2 x 2 y Solución: Podemos reescribir las ecuaciones como: x 2 y x 2 2 xy 4 y 2 x 2 y 2xy x 2 y x 2 y Obviamente cualquier par de números x y y que satisfacen la ecuación x 2 y 0 , será solución del sistema. Pero ahora asumamos que x 2 y 0 . Entonces podemos dividir entre x 2 y y obtenemos: x2 2 xy 4 y 2 1 2 xy 1 Luego: x 2y 2 x 2 4 xy 4 y 2 x 2 2 xy 4 y 2 6 xy 4 Consideramos dos casos: x 2 y 2 y x 2 y 2 En el primer caso: 1 2xy 2 2 2 y y 4 y 4 y2 0 4 y 2 4 y 1 2 y 1 1 ; x 2 2y 1 y 2 2 En el segundo caso: 2 x 2 2 y 1 2xy 2 2 2 y y 4 y 4 y 0 2 y 1 y 2 1 ; x 1 2 La solución del sistema son todos los pares x y y tales que x 2 y 0 , así como los pares x 1 ; y 1 1 y x 1 ; y 2 2 3. Si a, b, c son números reales positivos. Probar que: a 2b 2 b 2 c 2 c 2 a 2 a 3 b 3 c 3 ab bc ca 2 Solución: Por la media Harmónica – Media Geométrica tenemos: Por la media Aritmética – Media Geométrica tenemos: ab 2 1 1 a b a3 b3 2 a3b3 2ab ab Luego: a 2b 2 ab ab ab a 3 b3 ab 1 1 2 4 a b b2c 2 bc bc bc b3 c3 bc 1 1 2 4 b c c2a2 ca ca ca c 3 a 3 ca 1 1 2 4 c a (1) (2) (3) Sumando (1), (2) y (3): a 2b 2 b 2 c 2 c 2 a 2 a 3 b3 b3 c 3 c 3 a 3 a 3 b3 c 3 ab bc ca 4 4 4 2 4. El baricentro del triángulo ABC es G. Denotamos por g a , g b , g c las distancias desde G a los lados a, b y c respectivamente. Sea r el radio de la circunferencia inscrita. Demostrar que: ga 2r 2r 2r , gb , gc 3 3 3 Solución: Es sabe que uniendo G con cada vértice, se forman tres triángulos BGC de base a y altura ga , AGC de base b y altura gb y AGB de base c y altura gc de la misma área. Por tanto, llamando S al área de ABC: A c b gc gb G B ga a·ga = b·gb = c·gc = 2S 3 (1) C a Por otra parte sabemos que r·(a + b + c) = 2S (basta unir el centro con los tres vértices y quedan tres triángulos de bases a, b, c y altura común r). Sustituyendo 2S en (1), y despejando queda: r abc r abc r abc ; gb ; gc 3 a 3 b 3 c abc bc 1 2 , de donde y por la desigualdad triangular (b + c a) , resulta : a a 2r ga y de modo análogo para gb y gc . 3 ga 5. DETERMINE EL PRODUCTO DE TODOS LOS DIVISORES DE 2100 3100 . LOS DIVISORES DE 2100 ∙ 3100 TENDRÁN OBLIGATORIAMENTE LA FORMA 2𝑎 ∙ 3𝑏 , CON 0 ≤ 𝑎 ≤ 100, 0 ≤ 𝑏 ≤ 100. SI LOS ORDENAMOS DE FORMA MATRICIAL (SÓLO PARA PODER VISUALIZARLOS BIEN) TENDRÍAMOS UNA MATRIZ DE 101 FILAS Y 101 COLUMNAS: 20 ∙ 30 20 ∙ 31 20 ∙ 32 20 ∙ 3100 ⋯ 21 ∙ 3100 21 ∙ 30 21 ∙ 31 21 ∙ 32 22 ∙ 30 22 ∙ 31 22 ∙ 32 22 ∙ 3100 ⋮ ⋱ ⋮ 100 [2100 ∙ 30 2100 ∙ 31 2100 ∙ 32 ⋯ 2 ∙ 3100 ] Multiplicando cada fila tenemos: Primera fila : Segunda fila : Tercera fila : (ASÍ HASTA LA FILA 101) Fila 101 : SI MULTIPLICAMOS ESTOS BASE 2 OBTENEMOS: 101 (20 )101 ∙ (30 ∙ 31 ∙ 32 ∙ … ∙ 3100 ) (21 )101 ∙ (30 ∙ 31 ∙ 32 ∙ … ∙ 3100 ) (22 )101 ∙ (30 ∙ 31 ∙ 32 ∙ … ∙ 3100 ) (2100 )101 ∙ (30 ∙ 31 ∙ 32 ∙ … ∙ 3100 ) RESULTADOS PARCIALES Y AGRUPAMOS LOS QUE TIENEN [(20 )101 ∙ (21 )101 ∙ (22 )101 ∙ … ∙ (2100 )101 ][30 ∙ 31 ∙ 32 ∙ … ∙ 3100 ]101 = (20 ∙ 21 ∙ 22 ∙ … ∙ 2100 )101 ∙ (31 ∙ 32 ∙ 33 ∙ … ∙ 3100 )101 = (20+1+2+⋯+100 )101 ∙ (30+1+2+⋯+100 )101 = (25050 )101 ∙ (35050 )101 = 2510050 ∙ 3510050 = 6510050 6.- EN LA SIGUIENTE CONFIGURACIÓN DE 9 CÍRCULOS HAY SEIS MANERAS DE ELEGIR CUATRO CÍRCULOS DE MODO QUE LOS CENTROS DE LOS CUATRO CÍRCULOS SEAN LOS VÉRTICES DE UN CUADRADO REPRESENTEMOS CON UNA LETRA CADA UNO DE LOS CÍRCULOS DE LA FIGURA: ENTONCES SI “S” ES LA SUMA DE CADA UNO DE LOS 6 CUADRADOS TENEMOS: 𝑆 =𝑎+𝑏+𝑑+𝑒 𝑆 =𝑏+𝑐+𝑒+𝑓 𝑆 =𝑑+𝑒+𝑔+ℎ 𝑆 =𝑒+𝑓+ℎ+𝑖 𝑆 =𝑎+𝑐+𝑔+𝑖 𝑆 =𝑏+𝑓+ℎ+𝑑 SUMANDO MIEMBRO A MIEMBRO LAS CINCO PRIMERAS ECUACIONES, OBTENEMOS: 5𝑆 = 2𝑎 + 2𝑏 + 2𝑐 + 2𝑑 + 4𝑒 + 2𝑓 + 2𝑔 + 2ℎ + 2𝑖 5𝑆 = 2(𝑎 + 𝑏 + 𝑐 + 𝑑 + 𝑒 + 𝑓 + 𝑔 + ℎ + 𝑖) + 2𝑒 COMO 𝑎, 𝑏, 𝑐, 𝑑, 𝑒, 𝑓, 𝑔, ℎ, 𝑖 SON, EN ALGÚN ORDEN, 1,2,3,4,5,6,7,8,9 RESULTA: 5𝑆 = 2(1 + 2 + ⋯ + 9) + 2𝑒 5𝑆 = 90 + 2𝑒 DE AQUÍ SE SIGUE QUE 𝑒 ES MÚLTIPLO DE 5 (PUES 5𝑆 Y 90 LO SON) Y, POR LO TANTO, 𝑒 = 5. ADEMÁS, 90 + 2𝑒 90 + 10 𝑆= = = 20 5 5 HASTA AQUÍ TENEMOS QUE EL NÚMERO DEL CÍRCULO CENTRAL ES 5 Y QUE LA SUMA DE CADA CUADRADO ES 20. OBSERVEMOS QUE CADA UNO DE LOS NÚMEROS 𝑎, 𝑏, 𝑐, 𝑑, 𝑓, 𝑔, ℎ, 𝑖 ESTÁ POR LO MENOS UNA VEZ EN UN CUADRADO QUE TIENE AL 5. SI UN CUADRADO TIENE AL 1 Y AL 5, LA SUMA DE LOS OTROS DOS NÚMEROS ES 20 − 1 − 5 = 14. LA ÚNICA MANERA DE OBTENER 14 COMO SUMA DE DOS NÚMEROS DEL 1 AL 9 QUE NO UTILICE 1 NI 5 ES 14 = 6 + 8. ENTONCES, HAY SÓLO UN CUADRADO QUE SIMULTÁNEAMENTE EL 1 Y EL 5, DE MODO QUE EL 1 DEBE UBICARSE EN UNA ESQUINA DE LA CONFIGURACIÓN DE 9 CÍRCULOS (EN EL LUGAR DE 𝑎, 𝑐, 𝑔, 𝑖) Y SUS 2 VECINOS DEBEN SER EL 6 Y EL 8. PODEMOS UBICAR 𝑎 = 1, 𝑏 = 6, 𝑑 = 8. POR OTRA PARTE SI UN CUADRADO TIENE AL 3 Y AL 5, LA SUMA DE LOS OTROS DOS NÚMEROS ES 20 − 3 − 5 = 12. LA ÚNICA MANERA DE OBTENER 12 COMO SUMA DE DOS NÚMEROS DEL 1 AL 9 QUE NO UTILIZA AL 1 NI AL 3 NI AL 5 ES 12 = 4 + 8. LUEGO, AL IGUAL QUE EL 1, 3 DEBE UBICARSE EN UNA ESQUINA DE LA CONFIGURACIÓN Y SUS VECINOS DEBEN SER EL 4 Y EL 8. DE ACUERDO CON LAS ELECCIONES YA HECHAS, DEBEMOS PONER 𝑔 = 3, ℎ = 4. DE 20 = 𝑏 + 𝑓 + ℎ + 𝑑 = 6 + 𝑓 + 4 + 8, RESULTA 𝑓 = 2. DE 20 = 𝑏 + 𝑐 + 𝑒 + 𝑓 = 6 + 𝑐 + 5 + 2, RESULTA 𝑐 = 7. DE 20 = 𝑒 + 𝑓 + ℎ + 𝑖 = 5 + 2 + 4 + 𝑖, RESULTA 𝑖 = 9. CON ÉSTA CONFIGURACIÓN, LA SUMA DE LOS NÚMEROS EN LOS VÉRTICES DE LOS 6 CUADRADOS ES 20. HAY OTRAS DISTRIBUCIONES, PERO TODAS TIENEN EL 5 EN EL CÍRCULO CENTRAL Y EN EL BORDE SE ENCUENTRA LA SECUENCIA 1,8,3,4,9,2,7,6 RECORRIDA EN SENTIDO HORARIO O ANTI HORARIO, COMENZANDO POR EL 1 EN UNA ESQUINA