ESCUELA POLITECNICA DEL EJÉRCITO LABORATORIO DE
Anuncio
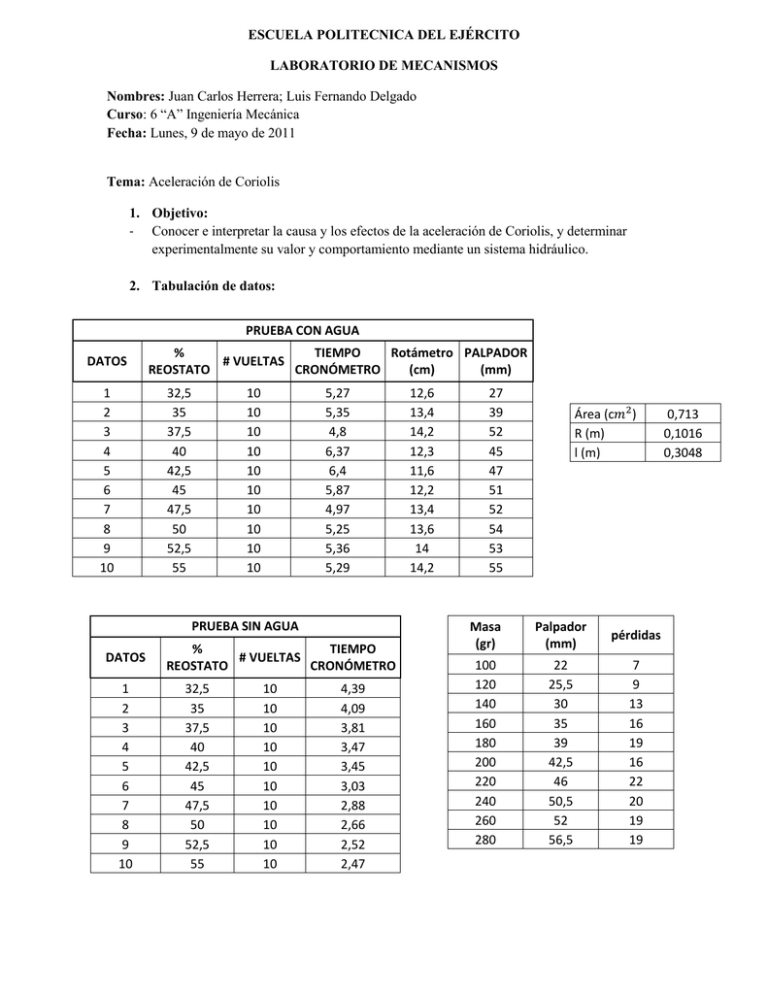
ESCUELA POLITECNICA DEL EJÉRCITO LABORATORIO DE MECANISMOS Nombres: Juan Carlos Herrera; Luis Fernando Delgado Curso: 6 “A” Ingeniería Mecánica Fecha: Lunes, 9 de mayo de 2011 Tema: Aceleración de Coriolis 1. Objetivo: - Conocer e interpretar la causa y los efectos de la aceleración de Coriolis, y determinar experimentalmente su valor y comportamiento mediante un sistema hidráulico. 2. Tabulación de datos: PRUEBA CON AGUA DATOS 1 2 3 4 5 6 7 8 9 10 % TIEMPO Rotámetro PALPADOR # VUELTAS REOSTATO CRONÓMETRO (cm) (mm) 32,5 35 37,5 40 42,5 45 47,5 50 52,5 55 10 10 10 10 10 10 10 10 10 10 5,27 5,35 4,8 6,37 6,4 5,87 4,97 5,25 5,36 5,29 PRUEBA SIN AGUA DATOS 1 2 3 4 5 6 7 8 9 10 % TIEMPO # VUELTAS REOSTATO CRONÓMETRO 32,5 35 37,5 40 42,5 45 47,5 50 52,5 55 10 10 10 10 10 10 10 10 10 10 4,39 4,09 3,81 3,47 3,45 3,03 2,88 2,66 2,52 2,47 12,6 13,4 14,2 12,3 11,6 12,2 13,4 13,6 14 14,2 27 39 52 45 47 51 52 54 53 55 Área (c𝑚2 ) R (m) l (m) Masa (gr) Palpador (mm) pérdidas 100 120 140 160 180 200 220 240 260 280 22 25,5 30 35 39 42,5 46 50,5 52 56,5 7 9 13 16 19 16 22 20 19 19 0,713 0,1016 0,3048 3. Resultados: PRUEBA CON AGUA CAUDAL (Lt/min) V (m/s) ac1 2VW RPS 10 10,62 11 9,75 9,25 9,75 10,62 10,65 11 11,25 2,337 2,481 2,570 2,278 2,161 2,278 2,481 2,488 2,570 2,629 55,717 58,286 67,290 44,943 42,438 48,771 62,743 59,564 60,259 62,444 2,278 2,445 2,625 2,882 2,899 3,300 3,472 3,759 3,968 4,049 w (rad/s) 14,313 15,362 16,491 18,107 18,212 20,737 21,817 23,621 24,933 25,438 Pérdidas vs w 25 Pérdidas (mm) 1,90 1,87 2,08 1,57 1,56 1,70 2,01 1,90 1,87 1,89 w (rad/s) 11,92 11,74 13,09 9,86 9,82 10,70 12,64 11,97 11,72 11,88 20 15 y = 1,011x - 4,124 10 5 0 0.00 5.00 10.00 15.00 20.00 25.00 30.00 w (rad/s) Fuerza vs lectura palpador 3 2.5 Fuerza (N) RPS PRUEBA SIN AGUA 2 1.5 y = 0,050x - 0,158 1 0.5 0 0 10 20 30 40 Lectura palpador (mm) 50 60 Fuerza (N) 0,980 1,176 1,372 1,568 1,764 1,960 2,156 2,352 2,548 2,744 PÉRDIDAS (mm) Δ (mm) FUERZA (F) TORQUE ac2 Error % 7,9271 7,7451 9,109 5,844 5,804 6,693 8,655 7,977 7,724 7,886 19,0729 31,2549 42,891 39,156 41,196 44,307 43,345 46,023 45,276 47,114 0,7956 1,404 1,9865 1,799 1,901 2,043 2,009 2,1431 2,105 2,197 0,081 0,143 0,202 0,183 0,193 0,208 0,204 0,218 0,214 0,223 12,2030679 21,5348257 30,4693242 27,5934127 29,1579086 31,3359322 30,8144336 32,8712855 32,2869003 33,6980143 78,098 63,053 54,719 38,603 31,293 35,749 50,888 44,814 46,420 46,035 a. Ejemplo de cálculos: - Prueba con agua: 𝑅𝑃𝑆 = #𝑣𝑢𝑒𝑙𝑡𝑎𝑠 𝑡𝑖𝑒𝑚𝑝𝑜 𝑅𝑃𝑆 = 10 𝑟𝑒𝑣 = 1.90 4.39 𝑠 𝑉= 𝑉= 𝑄 𝐴 𝑙𝑡 10 𝑚𝑖𝑛 0.713 𝑐𝑚 ∗ 2 1𝑚3 1𝑚𝑖𝑛 (100𝑐𝑚)2 ∗ ∗ (1𝑚)2 1000𝑙𝑡 60𝑠 𝑉 = 2.337𝑚/𝑠 𝑟𝑒𝑣 2𝜋 𝑟𝑎𝑑 𝑤 = 1.90 ∗ = 11.92 𝑟𝑎𝑑/𝑠 𝑠 1 𝑟𝑒𝑣 𝑎𝑐1 = 2 ∗ 𝑉 ∗ 𝑊 𝑎𝑐1 = 2 ∗ 2.337 ∗ 11.92 𝑎𝑐1 = 55.717𝑚/𝑠 2 De la grafica “Carta de Calibración: Para una lectura de rotámetro igual a 12.6, corresponde un calor de flujo de agua igual a 10 Lt/min - Prueba sin agua: 𝐹𝑢𝑒𝑟𝑧𝑎 = 100𝑔𝑟𝑓 ∗ 1𝐾𝑔𝑓 9.8𝑁 ∗ 1000𝑔𝑟𝑓 1𝐾𝑔𝑓 𝐹𝑢𝑒𝑟𝑧𝑎 = 0.140 𝑁 Realizamos las gráficas w vs pérdidas y Lectura del palpador vs fuerza, ambas gráficas para los datos de la prueba sin agua, una vez realizadas las gráficas obtenemos su ecuación. 𝐸𝑐. 𝑝é𝑟𝑑𝑖𝑑𝑎𝑠 = 1.011𝑥 − 4.124 𝐸𝑐. 𝐹𝑢𝑒𝑟𝑧𝑎 = 0.050𝑥 − 0.158 Para encontrar los valores de las pérdidas en la prueba con agua reemplazamos los valores obtenidos de w en la ecuación. Para encontrar los valores de la fuerza en la prueba con agua reemplazamos los valores obtenidos de la lectura del Palpador en la ecuación. → 𝑠𝑖 𝑥 = 11.92 ∴ 𝑝é𝑟𝑑𝑖𝑑𝑎𝑠 = 7.9271 → 𝑠𝑖 𝑥 = 19.072 ∴ 𝐹𝑢𝑒𝑟𝑧𝑎 = 0.795 𝑁 𝑇𝑜𝑟𝑞𝑢𝑒 = 𝐹𝑢𝑒𝑟𝑧𝑎 ∗ 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑖𝑎 𝑎𝑐2 = 𝑇𝑜𝑟𝑞𝑢𝑒 𝜌 ∗ 𝐴 ∗ 𝑙2 𝑇𝑜𝑟𝑞𝑢𝑒 = 0.795 ∗ 0.1016 𝑎𝑐2 = 𝑇𝑜𝑟𝑞𝑢𝑒 = 0.081 𝑁𝑚 0.081 𝑁𝑚 1000 𝐾𝑔 ∗ 0.713𝑐𝑚2 ∗ 0.30482 𝑚3 ∗ (100𝑐𝑚)2 (1𝑚)2 𝑎𝑐2 = 12.20 𝑚/𝑠 2 𝐸𝑟𝑟𝑜𝑟 = 𝑎𝑐1 − 𝑎𝑐2 ∗ 100% 𝑎𝑐1 𝐸𝑟𝑟𝑜𝑟 = 55.717 − 12.2 ∗ 100% 55.717 𝐸𝑟𝑟𝑜𝑟 = 78.0989 % 4. Aplicaciones: Se utiliza en el diseño de máquinas. Una aplicación práctica de la fuerza de Coriolis es el caudalímetro másico, un instrumento que mide el caudal másico de un fluido que circula a través de una tubería. El caudalímetro másico de Coriolis funciona aplicando una fuerza de vibración a un tubo curvado a través del cual pasa el fluido 5. Conclusiones: Esta práctica permitió observar cómo se genera la fuerza de Coriolis, y se comprobó de manera práctica los parámetros de los que depende. La fuerza de Coriolis es una fuerza que un observador de un sistema en rotación a velocidad angular constante ve actuar sobre un cuerpo, cuando este está en movimiento con respecto al sistema en rotación. De acuerdo a los resultados obtenidos y a los cálculos realizados, la aceleración de Coriolis está directamente relacionada con la velocidad de giro y la velocidad lineal tangente en cada punto de giro, es decir que cuando más rápido gira el disco mayor será la aceleración de Coriolis.







