SE-202-Enunciados de problemas_20121019

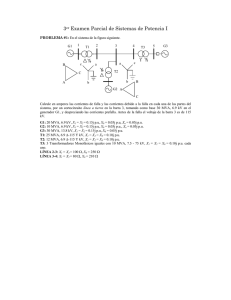
Ejemplo 2.1.A Determinar en el siguiente circuito serie: 1‐ La admitancia compleja (Solución: 0,05‐j0,05 siemens) 2‐ La intensidad en amperios (Solución: √ °
) 3‐ El cosφ (Solución: √ / ) 4‐ La tensión en bornes de la bobina y de la resistencia [Solución: 50√2 45° 50√2
45° ;
]
5‐ La potencia activa, reactiva y aparente (Solución: P=500 w; Q=500 var) 6‐ La potencia compleja (Solución: 500√2 45°
) 7‐ Diagrama vectorial de todo lo anterior Ejemplo 2.1.B Determinar el valor de la capacidad del condensador en μF a colocar en paralelo con la carga para que el cosφ de la carga sea de 0,8 inductivo.(Solución: , ) Ejemplo 2.2 En el adjunto esquema se representan dos máquinas síncronas iguales, la primera está trabajando como generador y alimenta a la segunda que está rebajando como motor en una central de bombeo. Sus características nominales son: G = M { SgN = 100 MVA; Xgp.u.= 0,2 p.u.; VgN= 10 kV;  = 600 r/m) Los transformadores T1 y T2 son idénticos y sus características nominales son: T1 = T2 { StN = 100 MVA; Xtp.u.=0,1 p.u.; rt = 100/10 kV} La impedancia de la línea es ZL = 0+ j 10 /f En un momento determinado el motor toma una potencia de 60 MW a 9,5 KV con factor de potencia 0,9 en adelanto. Se pide determinar: 1º) El circuito p.u. equivalente para los parámetros base que el alumno estime como más conveniente. 2º) La tensión, la f.e.m. del generador y la f.c.e.m. del motor en kV. (Solución: Vg=8,78kV[12,45]; Eg=8,57 kV[21,61]; Em=10,19 kV[‐7,12]) 3º) La intensidad en la línea en amperios (Solución: IL=405,18 A [25,84]) 4º) El par interno en el generador en kNw.m (Solución: C=954,92 kN.m) 5º) Diagrama vectorial de tensiones e intensidades correspondiente al circuito p.u. equivalente. Ejemplo 2.3 En el adjunto esquema la tensión en bornes del generador es 14,5 kV. Para unos parámetros base en la carga de SB = 20 MVA y VB‐3=69 kV. Se pide: 1º) Circuito p.u. equivalente. 2º) La tensión en kV en los puntos B, F y E. (Solución: VB=144,kV[‐3,63]; VF=71,28 kV[‐
10,79]; VE=142,98 kV[‐6,43]) 3º) Las intensidades en amperios en los distintos niveles de tensión del circuito. (Solución: IA=411,67[‐10,79]; IB=41,16A[‐10,79]; IF=82,33A[‐10,79]) 4º) La potencia compleja en la carga y en el generador. (Solución: SF=10,16+j0 MVA; SA=10,22+j1,95 MVA) 5º) El rendimiento de la línea. (Solución:=99,47%) La carga es de 500+j0 /f y las características de los transformadores son: T1{15 MVA, 14/140 kV, Xt1=0,10 p.u.}; y T2{10 MVA, 138/69 kV, Xt2=0,08 p.u.} Ejemplo 2.4 En el adjunto esquema las características del generador, transformador y línea son los siguientes: G{SgN = 50 MVA; Xgp.u. = 0,2 p.u.; VgN =4,5 kV}; T{StN= 50 MVA; Xtp.u.= 0,15 p.u.; rt = 45/4,5 kV} y ZL = j10 /f Determinar las potencias de cortocircuito en A), B) y C) después de cerrar K, si la potencia de cortocircuito de las barras A) es de 400 MVA con K abierto (Solución: SccA =483,76 MVA; SccB =277,29 MVA; SccC =345,80 MVA) Ejemplo 2.5 Un alternador trifásico de 10√3 kV; 60 MVA; Xsp.u.=1 p.u. y 1.500 r/m está acoplado a unas barras de potencia infinita. Determinar: 1º) La f.e.m. cuando suministra 1.000 A con cosφ=0.8 inductivo a tensión nominal. También PT, QT y θ así como la Psin/G.M. y Csin/G.M. (Solución: Ef =13,6 kV[107]; PT =24 MW; QT =18 MVAr;  =17; PSINC=2,7088 MW/gm; CSINC=17,24 kN.m) 2º) Desde la situación flotante se excita la máquina hasta que suministre 800 A sin actuar sobre el par, qué ST y f.e.m. tiene el alternador. (Solución: Ef =14 kV[90]; ST =0+j24 MVA) 3º) Partiendo de la situación anterior se disminuye la excitación hasta que la f.e.m. por fase vale 8 kV calcular la I y la ST. (Solución: I2 =0,4 A[‐180]; ST =0‐j12 MVA) Ejemplo 2.6 En el adjunto esquema unifilar la carga en las barras de A. T., es de S=10[‐10]MVA a una tensión de 145 kV. Se pide determinar: 1º) El circuito p.u. equivalente para unos parámetros base en la misma de: SB= 30 MVA y VB‐AT= 150 kV. 2º) Intensidad en A.T. y B.T. (Solución: IA =39,81A[10]; IA =398,14A [10]) 3º) La tensión en bornes del generador y su f.e.m. (Solución: VA =14,44 kV[1,61]; EA =14,34 kV[4]) Ejemplo 2.7 Dos alternadores se encuentran acoplados en situación flotante a las mismas barras sin alimentar carga alguna. Si el G2 sufre un retraso de 10 Mec., determinar el valor de la potencia y par sincronizante del G1 y del G2. G1<>G2 => 210 MVA; 15√3 kV; 3.000 r/m (Solución: PSINC=23,44 MW/gm; CSINC=7,46 x 10⁴ kN.m) Ejemplo 2.8 Determinar: 1) Tomando como parámetros base los del generador, determinar el circuito p.u. equivalente. 2) Si el motor está trabajando como tal y toma ¾ de carga con f.d.p. 0,9 en retraso y tensión de 14 kV. Calcular las tensiones en kV en A, B y C. (Solución: VA=16,50 kV[13,31]; VB=233,40 kV[10,61]; VC=211,87 kV[3,44]) 3) El rendimiento de la línea. (Solución:=98,45%) 4) La Psin/G.M. y Csin/G.M. en el motor para el punto de funcionamiento. (Solución: PSINC= XXX MW/gm; CSINC= XXX kN.m) Ejemplo 2.9 Dos líneas alimentan en paralelo a una carga de 200 MW y cos=0,85 inductivo a una tensión de 210 kV, tal como se indica en el adjunto esquema. Determinar: 1º) La potencia activa y reactiva transportada por cada línea. (Solución: S1= 104,5+j64,7 MVA; S2=105,5+j65,3 MVA) 2º) Tensión y potencia compleja en las barras de alimentación (A). (Solución: VA= 1,0039 [4,29]; SA=210+j153 MVA) 3º) Diagrama p.u. tomando como parámetros base SB = 225 MVA y VB = 220 kV. 4º) Valor de impedancia compleja en  a colocar en serie con LI para que el transporte la misma potencia compleja que LII. (Solución: X= XXX ) Ejemplo 2.10 Un transporte de A.T. está representado en un esquema unifilar en el adjunto esquema siendo las características de los transformadores, línea y carga las siguientes: T1{80 MVA; 13,5/135 kV; XT1=0,10 p.u.} T2{100 MVA; 138/69 kV; XT2=0,08 p.u.} ZL = 15+j60 /f y la carga es de 60+j30 [MW; MVAR]. Se pide determinar: 1º) El circuito p.u. equivalente tomando como parámetros base en la carga 100 MVA y 69 kV. 2º) La tensión en cada punto A, B, C y D de la red si la tensión de la barras D es de 66 kV. (Solución: VA=16,62 kV[14,32]; VB=158,92 kV[11,17]; VC=135,6 kV[2,97]) 3º) La potencia de cortocircuito en las barras C y D si se admite que no hay retorno de energía procedente de la carga y que las barras A son de potencia infinita. (Solución: SCC_C= 268 MVA; SCC_D= 221 MVA) Ejemplo 2.11 Un alternador trifásico de 120 MVA, 15 kV, 750 r/m, 0,25 p.u. de reactancia síncrona y resistencia despreciable está conectado a una red de potencia infinita de 14,5 kV. Dicho alternador está trabajando como motor síncrono en una central de bombeo y toma una carga con un ángulo de par de 15 eléctricos a factor de potencia unidad. Se pide: 1º) La intensidad y la f.c.e.m. del motor. (Solución: IS = 4,78 kA; Ef = 8,66 kV) 2º) La potencia tomada de la red. (Solución: PRED= 120,18 MW) 3º) Si se aumenta un 10% la excitación qué potencia compleja toma de la red. (Solución: SRED= 120,18 – j47,93 [MW ; MVAR]) 4 º) Diagrama vectorial. 5º) Describir de forma resumida el funcionamiento de una central hidroeléctrica. Ejemplo 2.12 Un alternador trifásico tiene como parámetros nominales los siguientes: 100 MVA, 20 kV, 600 r/m, Xs = 0,35 p.u. y cosφN = 0,85. Cuando trabaja a plena carga acoplado a una red de potencia infinita en el punto de funcionamiento nominal, se pide: 1º) El valor de la f.e.m. y el ángulo de par. (Solución: Ef = 24,42 kV[14,10]; =14,10) 2º) Si se reduce la excitación y el par hasta que entregue los ¾ de plena carga a cosφ constante e igual al nominal determinar la nueva f.e.m. y el nuevo ángulo de par. (Solución: Ef = 23,19 kV[11,09];  = 11,09) 3º) Si partiendo del punto anterior se aumenta sólo el par hasta el límite teórico de estabilidad determinar cuánto vale la potencia activa y la intensidad entregadas a la red y hacer comentarios sobre estos valores en una instalación turbina‐generador bien proyectada. 4º) Hacer un diagrama vectorial aproximadamente a escala en done se reflejen las situaciones anteriores. 5º) Demostrar que el acoplamiento en paralelo de dos máquinas síncronas es estable. Ejemplo 2.13 Dos alternadores idénticos están acoplados de forma que uno trabaja como generador y el otro como motor, tal como se indica en el adjunto esquema. El primero trabaja al 80% de su carga nominal a una tensión de 14,5 kV y cos n = 0,85 inductivo. Se pide: 1°) El circuito p.u. equivalente tomando corno parámetros base los nominales de las máquinas. 2°) La potencia compleja absorbida por el motor síncrono y el par interno del motor. (Solución: Sm= 86,82[10,77]MVA; CSINC= 1352,81 kN.m) 3°) La fe.m. del generador y contraelectromotriz del motor. (Solución: EG= 15,08[3,41]kV; EM = 12,33 [‐25,77]kV) 4°) Explica de forma resumida los pasos a seguir para acoplar un alternador a una red de potencia infinita. 5°) Razonar el rendimiento de una central reversible con turbinado y bombeo. Características: Sn= 125 MVA; Vn = 13,85 kV; cos n = 0,85; Xs= 0,10 p.u.; 600 r/m