Guia7 (Péndulo simple I)
Anuncio

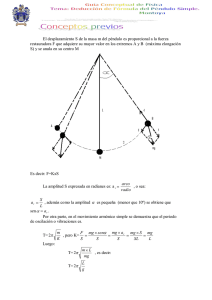
7.1 Objetivos 7 Péndulo Simple • Poner en práctica los métodos de análisis grafico para relaciones no lineales. • Establecer la relación existente entre los diferentes factores que afectan el período de un péndulo simple. 7.2 Introducción Una esfera suspendida de un hilo de manera que pueda oscilar alrededor de su posición de equilibrio, constituye un péndulo simple. La longitud del péndulo se mide desde el punto de suspensión hasta el centro de la esfera. La amplitud se mide como el desplazamiento horizontal de la masa con relación al punto de equilibrio. Periodo (T) es el tiempo de oscilación El péndulo se empezó a utilizar como instrumento de medida del tiempo a partir de Galileo. Apareciendo por esa época las leyes que lo rigen y que es el motivo de esta práctica. Es de anotar que a partir de ellas se puede determinar el valor de la gravedad en un lugar de la tierra. X = Amplitud Sen = X / L X = L Sen 7.3 Materiales • • • • • • • Calibrador. Cronómetro Pasco. 3 cilindros de diferente masa (cobre, acero, y bronce). Soporte universal. Regla graduada. Cuerda de acero. Balanza electrónica. 7.4 Recomendaciones: • • • • La longitud del péndulo se mide desde el punto de suspensión hasta el centro del cilindro. Para medir el período se coloca el cronómetro Pasco en el modo (pend) y en la escala 0,1 ms, cuya máxima lectura es de 1.999s. Se deja oscilar el péndulo partiendo del extremo (punto A en la grafica) y el cronómetro se activa automáticamente cuando el cilindro pasa por el punto B, el período de oscilación se completa (el cronómetro se desactiva automáticamente) cuando el cilindro pasa la tercera oportunidad por B. Al hacer oscilar el péndulo evite que éste golpee el sensor del cronómetro y cuide que el cilindro active el sensor. 7.5 Trabajo para desarrollar 7.5.1 Identificación del problema Si se hace oscilar un objeto que se encuentra suspendido por un hilo (péndulo simple) se pueden identificar los siguientes problemas: 1. ¿Si se varia la amplitud, varia el período de oscilación? 2. ¿Tendrá ingerencia la masa en la variación del periodo del péndulo? 3. ¿Dependerá el período de oscilación de la longitud del período? 7.5.2 Formulación de Hipótesis: A cada uno de los problemas identificados formule una o varias hipótesis en la forma lógica; si ___ entonces _____, teniendo cuidado de identificar las variables independientes y dependientes. 7.6 Toma de datos 7.6.1 Dependencia del período con la masa 1. Tome un péndulo de (1,00 m) de longitud y mida su masa. Para una amplitud inicial de 5º mida 30 veces el período de oscilación. 2. Repita sus mediciones para otras dos masas, asegurándose que la longitud del período usado sea siempre igual con la misma amplitud inicial. 3. Conociendo que el reloj de calibración del reloj Pasco es 1%; que existe un error de resolución y un error estadístico, halle el error al medir el período de oscilación para cada péndulo. 4. Estime el error en el proceso de la medida del periodo, la masa, la longitud y la amplitud; consulte los errores de calibración y resolución de los instrumentos utilizados. 5. Combine los errores anteriores en cuadratura, para determinar el error total en la medición de cada una de las cuatro cantidades utilizadas. 6. Elabore las tablas adecuadas para presentar sus datos, incluya en ellas los errores de las mediciones. 7.6.2 Dependencia del período con la amplitud 1. Deje el péndulo de longitud 1,00 m y la masa más densa constante. Para un ángulo de 5º mida 30 veces la oscilación. 2. Repita lo anterior para otras cinco (5) amplitudes; 10º, 25º, 35º, 45º. 3. Estime los errores en sus mediciones. 4. Elabore las tablas apropiadas para presentar sus datos. Incluya en ellas los errores de las mediciones. 7.6.3 Dependencia del período con la longitud 1. Deje el péndulo de masa y amplitud de 5º constantes. Para una longitud de 0.25 m, mida 30 veces el período de oscilación. 2. Repita lo anterior para cuatro (4) longitudes diferentes: 0.50m, 0.80m, 1.00m, 1.50m. 3. Estime los errores en sus mediciones. 4. Elabore las tablas apropiadas para presentar sus datos. Incluya en ellas los errores de las mediciones. 7.7 Análisis de datos 1. Para ver la dependencia del período con la masa, tome el período de la masa 1 como referencia y verifique si éste difiere de los períodos de las masas 2 y 3 en más de 1.96 del error toral. Si la diferencia es menor a 1.96 del error total se puede afirmar con un 95% de confiabilidad, que el período no depende de la masa. 2. Grafique el período en función del ángulo. Escoja adecuadamente la escala del período para que la gráfica ocupe el máximo de la hoja. Coloque el valor mínimo del período en el origen del sistema cartesiano. Calcule el error en el período T y marque en la gráfica el error mediante una barra. ¿Son las diferencias entre los valores del período mayores a 2 veces el error total? Justifique las respuestas en cifras. Si las diferencias son mayores. ¿Qué puede decirse de la dependencia del período con la amplitud? 3. Grafique el período en función de la longitud. Incluya el punto (0; 0) en la gráfica. Marque el error de cada medida en forma de cruz. ¿Es la relación hallada una línea recta? Aplique el tipo de regresión adecuada para linealizar dicha curva. Determine el exponente y la constante. 4. Compare con: y calcule el valor de la gravedad g. 5. De acuerdo a los resultados, ¿Son las hipótesis planteadas, falsas o verdaderas? Explique. 7.8 Conclusiones • • • • • Exprese mediante una relación matemática, como es la dependencia del período con los factores estudiados. ¿Son significativos los errores hallados en cada una de las partes ñeque se divide esta expresión? ¿Si se sustituyera la cuerda de acero por una de seda, qué diferencias se esperan? ¿Si la masa del cilindro se reemplaza por una de menor densidad, se afectará el experimento? ¿Qué otro tipo de conclusiones se pueden obtener de este experimento?