Deformación elástica - Raquel Serrano Lledó

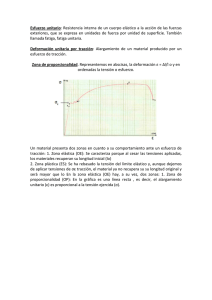
Introducción al comportamiento mecánico. Deformación elástica
TEMA 1
INTRODUCCION AL COMPORTAMIENTO MECÁNICO.
DEFORMACIÓN ELÁSTICA
1.- INTRODUCCIÓN
La producción y uso de los materiales está basada en gran parte en sus propiedades
mecánicas, es decir, en el comportamiento que manifiesta el material al ser sometido a la acción
de distintas cargas exteriores de cualquier tipo y naturaleza. Ante una acción exterior los
materiales reaccionan deformándose para contrarrestar la perturbación aplicada, esta deformación comienza siendo elástica si la tensión aplicada es pequeña, y la cantidad de deformación
elástica producida es también muy pequeña para metales y cerámicos, no ocurre así en polímeros en los que en algunos casos la deformación elástica es muy grande. La máxima deformación
elástica que tiene un material es generalmente el límite de diseño, dado que cuando se calcula
desde el punto de vista de resistencia un elemento cualquiera, se supone que en ningún momento el material se deforma permanentemente. Aunque esta ha sido norma general durante muchos años, hoy día se aceptan ciertas deformaciones permanentes controladas lo que obliga a un
mejor conocimiento del comportamiento del material y de las bases de cálculo.
La capacidad de deformación plástica de los metales es la característica más importante
en comparación con otros materiales. Todos los procesos de conformado, como laminación,
forja, extrusión, etc, están basados en la deformación plástica. Por otra parte, la naturaleza de
los mismos como órgano mecánico, esta basada en la capacidad de resistencia ante cargas
externas, en la capacidad de deformación, y en definitiva en la capacidad de funcionar correc-
1
Introducción al comportamiento mecánico. Deformación elástica
tamente sin llegar a romperse. Sin embargo, la fractura de los componentes mecánicos es un
hecho más común de lo que sería deseable.
Por todo lo anterior, el conocimiento de los mecanismos que producen la deformación y
rotura de los materiales es tremendamente importante en el campo de la ingeniería, para permitir la utilización más correcta de los mismos y prever sus fallos. También, la valoración de las
distintas propiedades mecánicas ante diversas fuerzas externas, es necesaria para el cálculo de
la resistencia en una aplicación concreta.
Esta valoración se realiza mediante el uso de ensayos patrón de distinta naturaleza,
como tracción, compresión, impacto, fatiga, etc, obteniendo la resistencia y el comportamiento
del material ante un esfuerzo determinado. Antes de definir y clasificar estos ensayos es necesario conocer los mecanismos que influyen en los mismos.
2. CONCEPTOS BÁSICOS
Antes de entrar en el comportamiento mecánico de los sólidos en general, vamos a
exponer la nomenclatura y a
definir los conceptos básicos de
tensión
y
deformación.
En
primer lugar definiremos el
concepto de tensión.
Consideremos un cuerpo
sólido sometido a un sistema de
Figura 1
fuerzas exteriores en equilibrio.
Supongamos
dicho
volumen
particionado en dos subvolúmenes con una superficie común. Cada uno de estos subdominios
debe a su vez estar en equilibrio. Si consideramos aislado el volumen 1,
2
Introducción al comportamiento mecánico. Deformación elástica
las fuerzas exteriores deben equilibrarse en este caso con las acciones interiores que ejerce el
volumen 2 sobre el 1 a través de la superficie común. La acción de un dominio sobre otro es
continua y podemos decir que se traduce en acciones locales de contacto ΔF asociado a una
superficie ΔS.
El vector tensión asociado en cada punto a una superficie se define como:
σ = lim
ΔS → 0
ΔF
ΔS
(1)
Nótese que la tensión tiene unidades de fuerza por unidad de superficie, al igual que una
presión, pero cuya dirección puede ser una cualquiera y no necesariamente normal a la superficie. Generalmente se suele descomponer el vector tensión en dos componentes, una normal a la
superficie que denotaremos σ y otra en el
plano tangente que denotaremos τ y denominaremos tangencial, de cizalladura o cortante.
La aplicación de distintas tensiones
sobre un cuerpo produce unas deformaciones,
también denominadas deformaciones normales o tangenciales según sean producidas por
una tensión normal o tangencial respectivamente.
Una tensión normal aplicada a un
elemento de volumen produce una variación
de longitud del material al que se aplica. En la
dirección de la tensión aplicada se produce
una deformación unitaria εn definida como la
variación de longitud dividida por la longitud
Figura 1
3
Introducción al comportamiento mecánico. Deformación elástica
inicial u/l. El alargamiento en la dirección de la fuerza aplicada (tracción), produce una contracción transversal en los dos ejes perpendiculares, la relación entre las deformaciones transversales inducidas (εt) y la deformación axial (εn) es conocido como módulo o relación de Poisson, y
viene definido como ν=-εt/εt. El signo negativo es debido a que εt es un acortamiento. Los
valores de ν varían entre 0,25 y 0,35 para los metales. Una tensión tangencial aplicada a un
elemento de volumen produce una variación de la forma del elemento de material y no un
cambio de volumen. La deformación cortante se representa por γ, y se define como w/l=tag θ,
Fig.2.
La ley de Hooke
En el campo elástico ambos conceptos están relacionados y siguen la llamada ley de
Hooke, según la cual, las deformaciones normales son proporcionales a las tensiones normales:
σ = Eε
(2)
donde E es el módulo de elasticidad o módulo de Young.
Igualmente las deformaciones tangenciales son proporcionales a las tensiones tangenciales que las provocan:
τ = Gγ
(3)
donde G es el módulo de elasticidad transversal.
Si un elemento de volumen está sometido a tensiones de compresión iguales en las seis
caras, fig. 2, el sólido experimenta una contracción reduciéndose su volumen en una cierta
cantidad ΔV. La reducción de volumen unitaria será ΔV/V, y considerando que la deformación
está dentro del campo elástico, es decir, se cumple ley de Hooke:
σ=B
ΔV
V
Todos estos parámetros están relacionados entre si por las siguientes expresiones:
4
(4)
Introducción al comportamiento mecánico. Deformación elástica
E = 2G (1 +ν )
(5)
E = 3B (1 - 2ν )
La figura 3 muestra la relación entre tensión y deformación para un material elástico
lineal perfecto, esta gráfica es simplemente una representación de la ley de Hooke. El área
rayada representa la energía
elástica por unidad de volumen
almacenada
por
el
material. En el proceso de
descarga el comportamiento
del material sigue la misma
línea,
energía
recuperándose
de
la
deformación
almacenada.
Figura 3
3. BASES FÍSICAS DEL MODULO DE ELASTICIDAD
El modulo de Young, que es la relación entre la perturbación mecánica aplicada a un
5
Introducción al comportamiento mecánico. Deformación elástica
material y su respuesta cuando el nivel de deformaciones es pequeño, da una idea de la rigidez
de un material, a mayor E mayor es la tensión que hay que aplicar a un material para conseguir
una deformación determinada.
Para comprender el significado físico del módulo de elasticidad es necesario analizar
que ocurre en el material a nivel atómico. Hay dos factores que afectan directamente al comportamiento del material:
Figura 4
(1) Las fuerzas que mantienen unidos los
átomos (enlaces interatómicos), que actúan
como pequeños muelles, uniendo un átomo al siguiente en estado sólido, Fig. 4.
(2) La forma de empaquetamiento de
los átomos (estructura), que determina
la cantidad de enlaces atómicos que se
concentra por unidad de área, y el
ángulo según el cual actúan.
Para los materiales metálicos y
cerámicos el factor de mayor influencia
es la naturaleza de los enlaces. El valor
Figura 5
de E también está influenciado por la
estructura cristalina tomando distintos
valores en función de la dirección cristalográfica en que se mida, E es generalmente el valor
medio de su magnitud en distintas direcciones (figura 7). Los valores de E para los metales y
cerámicas están en general entre 30 y 300 GPa.
6
Introducción al comportamiento mecánico. Deformación elástica
Figura 7
Figura 6
En los polímeros y elastómeros el módulo de
elasticidad es generalmente muy pequeño, estando
muy influenciado por los débiles enlaces secundarios que presentan estos materiales, además de
la capacidad de giro que tiene el enlace C-C, lo que permite que las largas cadenas moleculares
se estiren bajo la acción de una fuerza y después recuperen su posición inicial.
A nivel atómico el fenómeno que ocurre en metales y cerámicas es el siguiente: la
aplicación de una fuerza externa a un sólido cristalino supone la acción de esta fuerza sobre los
átomos, tratando de romper el equilibrio de fuerzas existentes en el enlace. Como la unión
sigue estando en equilibrio, habrá aparecido una fuerza interna que contrarresta a la aplicada,
esta fuerza es consecuencia de la separación de los átomos de sus posiciones de equilibrio,
apareciendo unas fuerzas de repulsión o atracción, según los átomos se acerque o alejen de sus
posiciones primitivas (Fig. 8). La suma de todas estas fuerzas generadas en el seno del sólido
contrarresta la fuerza perturbadora.
La desviación de los átomos de sus posiciones de equilibrio supone también la existencia de un estado energético superior al mínimo, almacenando el cristal una cantidad de energía
7
Introducción al comportamiento mecánico. Deformación elástica
superior a la que tendría en equilibrio en las condiciones en las que se encontraba. Fig. 2. La
separación por tanto de los átomos de su posición de equilibrio a pequeñas distancias, genera un
cambio de energía del sistema y produce una fuerza entre los átomos que trata de oponerse a la
perturbación producida.
Figura 8
La separación de los átomos de su posición de equilibrio para anular la fuerza exterior
aplicada, depende de la forma de la curva de enlace. Curvas muy tendidas alrededor de la
posición de equilibrio, necesitan más separación de los átomos para que aparezca la misma
fuerza que en otro material en que las ramas de la curva tienen una mayor pendiente. Por tanto
la forma de esta curva, o la de energía de enlace, tiene que estar relacionada con el modulo de
elasticidad. La rigidez de un enlace la podemos definir como:
8
Introducción al comportamiento mecánico. Deformación elástica
S=
dF d 2 U
= 2
dr
dr
(6)
dado que sabemos que la fuerza del enlace es dU/dr. S representa la pendiente de la curva, que
para pequeñas deformaciones podemos decir que se mantiene constante, por tanto la fuerza
entre dos átomos separados una distancia r, será:
F = S (r - r 0 )
(7)
siendo r0 la distancia de equilibrio del enlace. De una forma simple, si consideramos un sólido
de área unidad en el que hay N enlaces/unidad de área (figura 9), al que aplicamos una tensión
σ, al ser separados dos planos por efecto de la fuerza una distancia r-r0, se produce el siguiente
equilibrio de fuerzas:
σ = N S (r - r0 )
el número de enlaces por unidad de área es
(8)
1/ r 0 2 , ya que la superficie media por átomo
podemos suponer que es
r0
2
. La
separación de los átomos de su
posición de equilibrio dividido por
la separación inicial será la deformación unitaria, según se definió
en el apartado anterior, sustituyendo por tanto N por su valor y
poniendo la expresión anterior en
función de ε tendremos:
Figura 9
σ=
S (r - r 0 ) ⎛ S ⎞
= ⎜⎜ ⎟⎟ ε
2
r0
⎝ r0 ⎠
(9)
9
Introducción al comportamiento mecánico. Deformación elástica
Comparando la ecuación (5) con la ley de Hooke, se obtiene que E=S/r0. S puede
obtenerse a partir de las curvas de energía de enlace, y r0 a partir de la distancia de equilibrio
del enlace.
Esta explicación del módulo de elasticidad sirve para sólidos cristalinos o amorfos, que
no sean materiales poliméricos. En los polímeros y elastómeros el modulo de elasticidad es
generalmente muy pequeño y está muy influenciado por la temperatura variando varios órdenes de magnitud en función de T. En los metales y cerámicas la variación con la temperatura es
más pequeña, pudiendo disminuir el valor de E desde temperaturas próximas a el cero absoluto,
hasta casi la temperatura de fusión hasta un 60 %.
Debido a la dependencia del modulo elástico con el enlace, su valor se ve poco
influenciado por la adición de elementos de aleación, defectos de la red etc, dado que estos no
cambian sustancialmente las fuerzas de enlace del elemento base, siempre y cuando las cantidades de soluto no sean excesivamente altas. En las aleaciones con solubilidad total E variará
linealmente con la composición siguiendo la regla de las mezclas, si existen fases intermedias u
otras fases el comportamiento es similar, variando linealmente en función de la cantidad de
cada fase.
4. DEFORMACION PLASTICA
La mayoría de los sólidos presentan el comportamiento elástico anteriormente descrito para
niveles de tensión por debajo de un determinado valor llamado límite elástico, para solicitaciones mayores a este valor pueden ocurrir distintas cosas. Si la distancia entre los átomos hubiera
aumentado en una cantidad suficiente que la atracción entre los átomos deja de tener efecto, se
producirá la rotura del enlace y los átomos pueden separarse unos de otros. En este caso, el final
de la deformación elástica es la rotura o separación del sólido en dos o más partes. Sin embargo, la mayoría de los sólidos en ingeniería se deforman plásticamente antes de llegar a la rotura.
La deformación plástica es una deformación permanente del material, es decir, el material no
10
Introducción al comportamiento mecánico. Deformación elástica
recupera sus dimensiones originales cuando se deja de aplicar la carga. Esta deformación se
produce debido a que deslizan unas partes del material sobre otras. En los materiales policristalinos la deformación se debe al deslizamiento de planos cristalográficos, este comportamiento
esta muy influenciado por la naturaleza de los enlaces y el movimiento de dislocaciones, como
ya veremos. En los materiales poliméricos el deslizamiento de unas cadenas moleculares sobre
otras depende mucho de su estructura interna, el peso molecular, la cristalinidad, encadenamiento transversal y la rigidez de las cadenas, así como de la temperatura.
Al comenzar las deformaciones permanentes, si estas son factibles, la relación entre cargas y
desplazamientos, o entre tensiones y deformaciones deja de ser lineal (figura 10).
Figura 10
5. EL ENSAYO DE TRACCION
La evaluación más importante de la propiedades mecánicas de los materiales se hace
mediante el ensayo de tracción. El ensayo consiste en someter a una barra de sección circular o
rectangular, que recibe el nombre de probeta, a una carga de tracción que provoca el alargamiento continuo de la misma hasta que se produce su rotura. Como resultado del ensayo se
obtiene en forma gráfica la fuerza de tracción ejercida sobre la probeta en función del alargamiento producido.
11
Introducción al comportamiento mecánico. Deformación elástica
En el ensayo es evidente que tiene influencia la forma de la probeta, pues para una
misma fuerza aplicada y un mismo material se alargará más una probeta de menor sección que
otra más gruesa. Para independizar los resultados de la forma de la probeta y obtener valores
significativos para el material hay que establecer la relación entre la tensiones en el material y
las deformaciones unitarias que en este se producen. Si la carga se aplica de forma centrada se
repartirá uniformemente en cada sección transversal, la tensión soportada en cada punto será:
σ=
P
A
(10)
donde P es la carga aplicada y A es la sección transversal instantánea, puesto que cuando la
probeta se alarga su sección transversal disminuye.
La deformación unitaria, basada en el alargamiento será:
ε = ∫ll
0
l
dl
= ln
l
l0
(11)
Sin embargo, en el uso práctico de la ingeniería, a partir de los datos del ensayo se suele
obtener la relación entre tensión y deformación definidas como:
tension S =
P
A0
l - l 0 Δl
deformacion e =
=
l
l0
12
(12)
Introducción al comportamiento mecánico. Deformación elástica
En la figura 11 se representan
ambas curvas, cuando las deformaciones son pequeñas la disminución de
la sección de la probeta es despreciable
y ambas curvas prácticamente coinciden. Sin embargo, cuando haya una
deformación importante en la probeta
hay que tener en cuenta las secciones y
longitudes reales de la misma, para
determinar en cada momento, las
Figura 11
cargas unitarias y alargamientos verdaderos.
A partir de los datos del ensayo, pueden determinarse las siguientes características del
material:
-
límite elástico (σe) o valor de la tensión a partir de la cual aparecen deformaciones
permanentes.
- Resistencia a la tracción (σr) o tensión para la que se produce la rotura de la probeta.
- Alargamiento longitudinal producido.
- Reducción de la sección transversal de la probeta.
- Módulo de elasticidad longitudinal (módulo de Young, E) del material.
Según las curvas de tensión-deformación en un ensayo de tracción, se pueden observar
tres comportamientos generales, a) materiales que tienen deformación elástica y plástica, b) los
que no tienen prácticamente deformación plástica y se rompen inmediatamente después de la
deformación elástica, y c) los que muestran fundamentalmente una gran deformación elástica.
En la figura 12 se recogen las gráficas de estos comportamientos.
13
Introducción al comportamiento mecánico. Deformación elástica
Figura 12
Además del límite elástico y la tensión de rotura, para caracterizar los distintos comportamientos de los materiales, son de gran interés otras propiedades mecánicas como la ductilidad, tenacidad y dureza de los materiales.
Ductilidad, es la capacidad de un material de deformarse permanentemente antes de
romper. Un material que experimenta muy poca o ninguna deformación plástica hasta la
fractura se denomina frágil. Una medida de la ductilidad del material es el porcentaje de elongación o de reducción de área, obtenido del ensayo de tracción tras la rotura:
14
Introducción al comportamiento mecánico. Deformación elástica
%EL =
l f - l0
100
l0
(13)
%RA =
A f - A0
100
A0
donde l0 y A0 son la longitud y area iniciales de la probeta y lf y Af dichas magnitudes después
de la rotura.
Conocer la ductilidad de un material es importante por dos razones. Primero, indica al
diseñador el grado de deformación que alcanzará la estructura o componente antes de la fractura. Segundo, indica el grado de deformación permitida durante los procesos de fabricación.
Tenacidad, es un término mecánico que se usa en diversos conceptos. Como característica general podemos decir que la tenacidad es una medida de la capacidad del material de
absorber energía antes de la rotura, o dicho de otra forma, es el trabajo por unidad de volumen
requerido para causar la fractura del material. Dicho trabajo será:
Trabajo = ∫( fuerza, P )( incremento de_longitud, dl )
(14)
Trabajo por unidad de volumen = ∫
P dl ε f
= ∫ 0 σ dε
A
La tenacidad por tanto, representa el área bajo la curva σ-ε. Generalmente los materiales tenaces suelen tener resistencia y ductilidad moderadamente altas. Los materiales de alta
resistencia y baja ductilidad tienen baja tenacidad (generalmente la ductilidad disminuye
cuando la resistencia aumenta).
Dureza, es una medida de la resistencia a la penetración sobre la superficie de un
material. La determinación de la dureza se hace generalmente por ensayos de penetración.
Estos consisten en producir una huella en el material que se ensaya aplicando sobre este un
15
Introducción al comportamiento mecánico. Deformación elástica
penetrador con una presión determinada. El índice de dureza se halla en función de la presión
que se ejerce y la profundidad o diámetro de la huella. Los métodos más usados son los de
Brinell, Rockwell y Vickers, según el método empleado las escalas de medida son distintas.
En definitiva, la dureza es una medida de la resistencia del material a la deformación
plástica localizada. Los conceptos de resistencia a tracción y dureza están directamente
relacionados. Para los aceros la tensión de rotura puede estimarse como:
σ r (MPa)= 3.45HB
donde HB es la dureza Brinell.
16
(15)