Proyecto 6 - Raquel Serrano Lledó

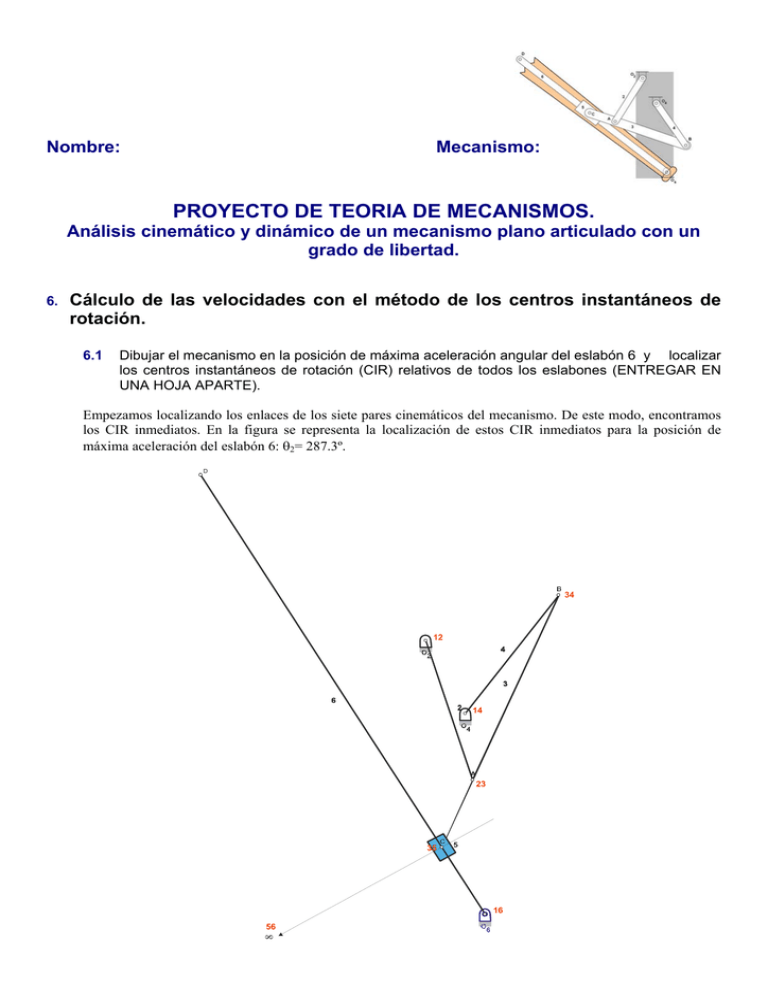
Nombre:
Mecanismo:
PROYECTO DE TEORIA DE MECANISMOS.
Análisis cinemático y dinámico de un mecanismo plano articulado con un
grado de libertad.
Cálculo de las velocidades con el método de los centros instantáneos de
rotación.
6.1
Dibujar el mecanismo en la posición de máxima aceleración angular del eslabón 6 y localizar
los centros instantáneos de rotación (CIR) relativos de todos los eslabones (ENTREGAR EN
UNA HOJA APARTE).
Empezamos localizando los enlaces de los siete pares cinemáticos del mecanismo. De este modo, encontramos
los CIR inmediatos. En la figura se representa la localización de estos CIR inmediatos para la posición de
máxima aceleración del eslabón 6: 2= 287.3º.
D
34
12
14
23
35
16
56

6.
Para encontrar el resto de los CIR, aplicaremos el teorema de los tres centros. Para facilitar la aplicación de este
teorema, dibujamos un polígono de 6 lados, donde cada vértice representa un eslabón, y cada lado o diagonal el
CIR relativo entre los dos eslabones de los vértices que une. En la siguiente figura se representa dicho polígono,
con las líneas representando los CIR inmediatos en negro y el resto en rojo, así como la secuencia utilizada para
calcular todos los CIR.
1
6
1º
12-23
14-34
} 13
2º
12-14
34-23
} 24
16-13
3º 35-56
} 36
16-12
4º 23-36
} 26
5º
26-56
23-35
} 25
6º
16-56
12-25
} 15
14-15
7º 34-35
} 45
16-14
56-45
} 46
2
3
5
4
8º
Como ejemplo, en la siguiente figura se representa como se puede calcular el 1er CIR, el 13, con la intersección
de las líneas que unen los CIRs 12-23 y 14-34.
34
12
14
13
23
35

56
16
A continuación se muestra el esquema del mecanismo mostrando la localización de todos los CIR.
D
34
12
14
13
24
23
46
45
35
36
26
25
16

56
15
6.2
Utilizando los CIR obtenidos, calcular la velocidad de los puntos D y C3=C5, para una 2 =
1rad/s en sentido horario.
CALCULO DE LA VELOCIDAD DE C5
Para calcular la velocidad del punto C a partir de w2, vamos a considerar que el punto C pertenece al eslabón 5, por
lo que necesitaremos los CIR 12, 15 y 25.

Calculamos gráficamente la velocidad del punto 25 considerando que pertenece al eslabón 2 y por tanto gira
alrededor de 12. En este caso calcularemos la velocidad de 25 partiendo de la velocidad de A.
1- Calculamos la velocidad del punto A y la representamos a escala en el mecanismo. La dirección será
perpendicular a la línea 12-A y su módulo tendrá un valor de v A  2  12 A  1rad / s  8 cm  8 cm/ s
2- Haciendo centro en 12 abatimos el punto A sobre la línea 12-25 y encontramos el punto A’. La velocidad de
A’ será igual en módulo a VA y su dirección perpendicular a 12-A’.

3- Trazamos una línea recta que pase por el extremo del vector VA ' y por 12.
4- Trazamos la dirección de la velocidad V25 (perpendicular a 12-25).
5- La intersección entre las dos líneas nos da el módulo de V25.
Analíticamente podemos hacer el mismo cálculo. Para ello necesitamos conocer la distancia 12-25. Medimos en
el dibujo y aplicamos el factor de escala: 12-25= 12.8 cm
Podemos calcular el módulo de la velocidad del punto 25 del eslabón 2 como:
v25  2 12 25  1rad/ s 12 .8 cm  12 .8 cm/ s

Calculamos gráficamente la velocidad del punto C5:
1- Consideramos ahora que el punto 25 pertenece al eslabón 5 y por lo tanto gira alrededor de 15

2- Trazamos una línea recta que pase por el extremo del vector V25 y por el centro de giro 15.
3- Haciendo centro en 15 abatimos el punto C5 sobre la prolongación de la línea 15-25 y encontramos el punto
C5’.


4- Trazamos la dirección de la velocidad VC5 ' (perpendicular a 15-C5’) y encontramos el módulo de VC5 '


5- El vector velocidad de VC5 tendrá el mismo módulo que VC5 ' y dirección perpendicular a su radio de giro (15C). Midiendo en el dibujo y aplicando el factor de escala de velocidades, obtenemos VC5 = 17.7 cm/s
Para calcular esta velocidad analíticamente necesitamos las distancias 15-25 y 15-C5.
15-25= 38.4 cm
15-C5= 53.2 cm
Podemos calcular la velocidad 5 como:
5 
v25
12 .8 cm/ s

 0.33rad / s (sentido antihorario)
15 25 38 .4cm
A partir de este valor, calculamos la velocidad de C5:
vC5  5 15  C5  17.7 cm/ s
D
12
VA`
VA
A`
Vc5
V25
25
15
0 cm/s
25 cm/s
50 cm/s
c5`
Vc5`
CALCULO DE LA VELOCIDAD DEL PUNTO D
Para calcular la velocidad del punto D, vamos a considerar que el punto A pertenece al eslabón 2. Como el punto E
pertenece al eslabón 6, necesitaremos los CIR 12, 16 y 26.

Calculamos la velocidad del punto 26 considerando que pertenece al eslabón 2 y por tanto gira alrededor de 12.
Para ello:
1-
Calculamos la velocidad del punto A, con dirección perpendicular a la línea 12-A y módulo
v A  2  12 A  1rad / s  8 cm  8 cm/ s
2345-
Haciendo centro en 12 abatimos el punto A sobre la línea 12-26 y encontramos el punto A’. Su velocidad
tendrá el módulo de VA y dirección perpendicular a 12-A’.
Trazamos una línea recta que pase por el extremo del vector VA y por 12.
Trazamos la dirección de la velocidad V26 (perpendicular a 12-26).
La intersección entre las dos líneas nos da el módulo de V26.
Analíticamente podemos hacer el mismo cálculo. Para ello necesitamos conocer el radio de giro del punto 26
respecto al centro de giro del eslabón 2:
12-26=11.7 cm
Podemos calcular la velocidad del punto 26 del eslabón 2 como:
v26  2 12  26  1 rad / s 11.7 cm  11.7 cm/ s

Calculamos la velocidad del punto D:
12345-
Consideramos ahora que el punto 26 pertenece al eslabón 6 y por lo tanto gira alrededor de 16.
Trazamos una línea recta que pase por el extremo del vector V26 y por el centro de giro 16.
Haciendo centro en 16 abatimos el punto D sobre la línea 16-26 (punto D’).
Trazamos la dirección de la velocidad V D’ (perpendicular a 16- D’) y encontramos el módulo de VD’
El vector velocidad de VD tendrá el mismo módulo que VD’ y dirección perpendicular a su radio de giro
(16-D). Midiendo en el dibujo y aplicando el factor de escala de velocidades, obtenemos VD = 92.2 cm/s
Para calcular esta velocidad analíticamente necesitamos las distancias 16-26 y 16-D.
16-26 = 3.5 cm
16-D = 28 cm
Podemos calcular la velocidad 6 como:
6 
v26
11.7cm/ s

 3.3 rad / s (sentido antihorario)
16 26
3.5cm
A partir de este valor, calculamos la velocidad de D:
vD  6 16  D  3.3 rad / s  28 cm  92 .4 cm/ s
D`
VD`
D
VA`
A`
VD
12
VA
26
V26
0 cm/s
6.3
50 cm/s
100 cm/s
16
Introducir el mecanismo en el programa Winmecc. Obtener la velocidad de los puntos D y
C3=C5. Rellenar la siguiente tabla con los resultados:
Módulos de las velocidades
Eslabón/
Punto
2
C3=C5
D
Método CIR
Winmecc
1 rad/s
(s. horario)
17.7 cm/s
92.4 cm/s
1 rad/s
(s. horario)
17.4 cm/s
91.5 cm/s