Unidad 3, Parte 1

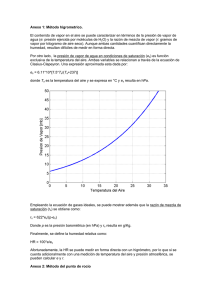
Cátedra de Introducción a las Ciencias de la Atmósfera
Introducción a las Ciencias de la Atmósfera
Unidad 3, Parte 1: Humedad
Ecuación de estado de gases ideales
La relación entre la presión, la densidad y la temperatura viene dada por la “ecuación
de estado”. En el caso de los gases ideales, la ecuación de estado o “ley de los gases
ideales” se expresa como
P = ρ RT
siendo P la presión del aire, ρ la densidad, R la constante del gas definida como R* /
M, siendo R* la constante universal de los gases (R* = 8,3143 J kg –1 K – 1), M el peso
molecular y T la temperatura (absoluta).
Mezcla de gases ideales
La ecuación de estado para una mezcla de gases ideales se expresa como
P = ρRT
siendo P, ρ y T la presión, densidad y temperatura, respectivamente, y la constante
R=
∑m R
i
m
i
, en donde Ri es la constante de cada gas ideal, mi su masa y m la masa
de la mezcla dada por
m = ∑mi
. En una mezcla de gases ideales se cumple la Ley
de Dalton, de manera tal que la presión total P viene dada por la suma de las
denominadas presiones parciales Pi de cada gas
P = ∑Pi
.
1
Cátedra de Introducción a las Ciencias de la Atmósfera
Aire seco
Se define como aire seco a la mezcla de gases de composición constante definida en
clases anteriores. Teniendo en cuenta los rangos de temperatura y de presión que se
observan en la atmósfera, el aire seco se comporta como un gas ideal, cuya ecuación
de estado viene dada por
P = ρ Rd T
en donde Rd = 287 J kg –1 K – 1 es la constante del gas para el aire seco.
Aire húmedo
Se define como aire húmedo a la mezcla de aire seco y vapor de agua, este último
también considerado como un gas ideal. La ecuación de estado para el aire húmedo
queda
P = ρRT
en donde R = (1 + 0,608q) Rd , siendo
q=
mv
m la relación entre la masa de vapor de
agua mv y la masa de aire húmedo m, denominada humedad específica. Es decir que,
si bien a R se la conoce como la constante del gas para el aire húmedo, su valor dista
de ser una constante ya que depende del contenido de vapor de agua en el aire. La
ecuación de estado para el aire húmedo se puede reescribir como
P = ρRd Tv
en donde Rd es la constante del gas para el aire seco y Tv = (1 + 0,608q )T es la
denominada temperatura virtual. Esta última se define entonces como la temperatura
del aire seco a la misma presión y densidad que el aire húmedo considerado.
2
Cátedra de Introducción a las Ciencias de la Atmósfera
Saturación
Se dice que el aire se encuentra saturado cuando el contenido de vapor de agua
alcanza el máximo valor que el aire puede contener. Cuando el aire contiene una
cantidad de vapor menor a este valor, éste se encuentra no saturado. La presión
parcial del vapor de agua se denomina presión o tensión de vapor, y se la representa
con el símbolo e. El valor de la presión de vapor correspondiente a la saturación se
indica mediante el símbolo es. Para el aire no saturado, e < es. Resulta sumamente
raro encontrar aire sobresaturado en la atmósfera, en cuyo caso e > es.
El aire caliente puede contener mayor vapor de agua que el aire frío. La ecuación de
Clausius-Clapeyron representa la relación entre la temperatura y la presión de vapor
de saturación, que se puede escribir en forma aproximada como
L
e s = e0 ⋅ exp 
 Rv
 1 1 
⋅  − 
 T0 T 
en donde e0 = 0,611 kPa y T0 = 273 K son parámetros constantes. Rv = 461 J K–1 kg–1
es la constante del gas para el vapor de agua. En la fórmula se utiliza la temperatura
absoluta, expresada en grados Kelvin.
Dado que las nubes pueden estar constituidas por gotas líquidas y cristales de hielo
suspendidos en el aire, debemos considerar saturaciones con respecto al agua y al
hielo. Para el caso de la saturación con respecto al agua líquida, utilizamos el calor
latente de vaporización L = Lv = 2,5×106 J kg–1 en la ecuación de Clausius-Clapeyron,
en cuyo caso L / Rv = 5423 K. En el caso de considerar la saturación con respecto al
hielo, usamos el calor latente de deposición L = Ld = 2,83×106 J kg–1 , en cuyo caso L /
Rv = 6139 K.
Variables de humedad
Relación de mezcla
3
Cátedra de Introducción a las Ciencias de la Atmósfera
La relación entre la masa de vapor mv y la masa de aire seco md está definida por la
relación de mezcla w:
w=
ε=
donde
mv
ε ⋅e
=
md P − e
Rd
= 0,622
Rv
, es decir la relación entre las constantes de los gases del
vapor y del aire seco.
T
es
Td
(°C)
-20
-18
-16
-14
-12
-10
-8
-6
-4
-2
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
32
34
e
(kPa)
0,127
0,150
0,177
0,209
0,245
0,287
0,335
0,391
0,455
0,528
0,611
0,706
0,814
0,937
1,076
1,233
1,410
1,610
1,835
2,088
2,371
2,688
3,042
3,437
3,878
4,367
4,911
5,514
ws
o sino
w
(g/kg)
0,78
0,92
1,09
1,28
1,51
1,77
2,07
2,41
2,80
3,26
3,77
4,37
5,04
5,80
6,68
7,66
8,78
10,05
11,48
13,09
14,91
16,95
19,26
21,85
24,76
28,02
31,69
35,81
qs
ρvs
q
(g/kg)
0,78
0,92
1,09
1,28
1,51
1,76
2,06
2,40
2,80
3,25
3,76
4,35
5,01
5,77
6,63
7,60
8,70
9,95
11,35
12,92
14,69
16,67
18,89
21,38
24,16
27,26
30,72
34,57
ρv
(kg/m3)
0,00109
0,00128
0,00150
0,00175
0,00204
0,00237
0,00275
0,00318
0,00367
0,00422
0,00485
0,00557
0,00637
0,00728
0,00830
0,00945
0,01073
0,01217
0,01377
0,01556
0,01755
0,01976
0,02222
0,02494
0,02794
0,03127
0,03493
0,03896
4
Cátedra de Introducción a las Ciencias de la Atmósfera
36
38
40
42
44
46
48
50
6,182
6,921
7,736
8,636
9,627
10,717
11,914
13,228
40,43
45,61
51,43
57,97
65,32
73,59
82,91
93,42
38,86
43,62
48,91
54,79
61,31
68,54
76,56
85,44
0,04340
0,04827
0,05362
0,05947
0,06588
0,07287
0,08051
0,08884
Tabla 1 Valores de saturación de humedad para distintos valores reales de temperatura
del aire, o sino valores reales de humedad para distintas temperaturas de rocío.
(Adaptada de Stull, 1995).
La relación de mezcla de saturación, ws, se define como w pero tomando es en lugar
de e en la fórmula. En la Tabla 1 se dan algunos valores de relación de mezcla para el
aire a nivel del mar.
Si bien la relación de mezcla se expresa en g / g (es decir en gramos de vapor por
gramo de aire seco), se la suele expresar en g / kg (es decir, en gramos de vapor por
kilogramo de aire seco).
Humedad específica
La relación entre la masa de vapor de agua y la masa total de aire (húmedo) se
denomina humedad específica q:
q=
mv ε ⋅ e
≅
m
P
Al igual que la relación de mezcla, la humedad específica se expresa en unidades de
g / kg. La humedad específica de saturación se obtiene utilizando es en lugar de e en
la fórmula anterior. La relación entre la humedad específica y la relación de mezcla
viene dada por
q=
w
1+w
En la Tabla 1 se observa que w << 1 (expresado en g / g), con lo cual se puede
aproximar bastante bien la igualdad entre ambas variables de humedad, es decir
5
Cátedra de Introducción a las Ciencias de la Atmósfera
q≈w
Tanto la relación de mezcla como la humedad específica de saturación dependen de
la presión atmosférica, a diferencia de la presión de vapor de saturación (que solo
depende de la temperatura, ver Fa. de Clausius–Clapeyron). Esto significa que, los
valores de presión de vapor en la Tabla 1 representan cantidades absolutas mientras
que las otras variables de humedad son válidas únicamente a la presión y densidad
del aire a nivel del mar. Los valores de saturación de la relación de mezcla y la
humedad específica se pueden calcular para cualquier otra presión atmosférica
empleando las fórmulas dadas.
Humedad absoluta
A la concentración, ρv, de vapor de agua en aire se la denomina humedad absoluta, y
se expresa en unidades de gramos de vapor por metro cúbico (g / m 3). La humedad
absoluta es esencialmente una densidad parcial, por lo tanto puede ser determinada a
partir de la presión parcial utilizando la ecuación de gases ideales para el vapor de
agua:
ρv =
e
e
= ⋅ ε ⋅ ρd
Rv ⋅ T P
en donde ρd es la densidad del aire seco. La densidad del aire es ρd = 1,225 kg / m3 a
nivel del mar, y varía con la altura, la presión, y la temperatura de acuerdo con la ley
de los gases ideales.
El valor de saturación de la humedad absoluta, ρvs, se obtiene sustituyendo es en
lugar de e en la ecuación anterior.
Humedad relativa
La relación entre el contenido real de vapor de agua en el aire y el contenido máximo
(saturación) que éste podría sostener a la misma temperatura viene dada por la
humedad relativa, HR:
6
Cátedra de Introducción a las Ciencias de la Atmósfera
q
HR
e
w
=
=
≈
100% e s q s ws
La humedad relativa indica la cantidad de evaporación que es posible en el aire. El
aire saturado tiene HR = 100%, y no permite evaporación de agua. La Tabla 1 muestra
la variación de la relación de mezcla con la HR. Es común expresar a la humedad
relativa en forma fraccional, en cuyo caso se la expresa como r, o sea
r=
HR
100% .
Cuando el aire se encuentra saturado, es decir HR = 100%, entonces r = 1.
Temperatura de punto de rocío
Se denomina temperatura de punto de rocío, Td, a la temperatura a la cual el aire
debe ser enfriado para tornarse saturado a presión constante. Ésta se puede obtener
de la ecuación de Clausius-Clapeyron (o de la Tabla 1) haciendo uso de e en lugar de
es, y Td en vez de T. Luego, resolviendo para Td se obtiene:
1 R
 e 
Td =  − v ⋅ ln 
L
T0
 es 
−1
Normalmente, para obtener la temperatura de rocío se considera L = Lv. Si se desea
obtener la temperatura del punto de escarcha debido a la presencia de cristales de
hielo en el aire, se utiliza L = Ld.
Si Td = T, el aire se encuentra saturado. La depresión del punto de rocío (T – Td) es
una medida relativa de la sequedad del aire. T nunca puede ser menor que Td. Si el
aire es enfriado por debajo de la temperatura inicial de punto de rocío, entonces la
temperatura del punto de rocío disminuye de manera tal que permance en todo
momento igual a la temperatura del aire, y el excedente de agua se condensa como
rocío, niebla o nubes.
La relación entre la depresión del punto de rocío y la humedad relativa se expresa
mediante la siguiente relación:
7
Cátedra de Introducción a las Ciencias de la Atmósfera
T − Td ≈ −35 ⋅ log r
Temperatura de bulbo húmedo
Cuando el bulbo de un termómetro es recubierto con una tela humedecida con agua
pura, se torna más frío y adquiere una temperatura menor que la temperatura real del
aire T (indicada por el termómetro de bulbo seco) debido al calor latente asociado con
la evaporación del agua. El aire más seco permite mayor evaporación, haciendo que la
temperatura de bulbo húmedo Tw descienda significativamente por debajo de la
temperatura del aire. En el aire saturado no hay evaporación neta y la temperatura de
bulbo húmedo iguala a la de bulbo seco.
Para asegurar un buen funcionamiento, el bulbo húmedo debe tener una buena
ventilación ya sea haciendo circular aire a través de él o moviendo el termómetro a
través del aire. En las estaciones meteorológicas, en general el psicrómetro se
encuentra montado dentro del abrigo meteorológico y consiste en un soporte que
sostiene a los termómetros de bulbo húmedo y bulbo seco.
Consideremos la temperatura de bulbo húmedo Tw y la relación de mezcla ww del aire
que envuelve al bulbo húmedo tras haberse evaporado el agua de la tela húmeda.
Debido a que el calor latente consumido para la evaporación es sustraído en forma de
calor sensible a modo de enfriamiento, el balance de calor establece que:
C p ⋅ (T − Tw ) = −Lv ⋅ ( w − ww )
Si se conocen las temperaturas de bulbo seco y bulbo húmedo, y la presión del aire
P, la relación de mezcla ww se obtiene mediante:
ww =
ε
 − c ⋅ Tw 
 − 1
b ⋅ P ⋅ exp
T
+
α
 w

w = ww − β ⋅ ( T − Tw )
8
Cátedra de Introducción a las Ciencias de la Atmósfera
en donde las temperaturas deben ser expresadas en °C, ε = 0,622 g / g, b = 1,631
kPa–1, c = 17,67, α = 243,5 °C, y β = 4,0224 × 10–4 (g / g)/°C. Conociendo w, se puede
obtener fácilmente cualquier otra variable de humedad.
Agua precipitable
Si se condensara el vapor de agua contenido en una columna atmosférica de 1 m 2 de
sección, el espesor de la masa de agua líquida contenida en dicha columna expresado
en milímetros, indica el valor del agua precipitable m. Es decir, que el agua precipitable
se define como la precipitación que resulta de condensar el contenido total de vapor
de agua en una columna atmosférica. Por lo tanto, este parámetro de humedad
constituye una medida del contenido de vapor de agua en la atmósfera.
La distribución vertical del vapor de agua se puede determinar a partir de
radiosondeos. Para cada capa dz de 1 m 2 de sección se puede determinar el
contenido de vapor de agua dm:
e
⋅ dz
Rv ⋅ T
dm = ρ v ⋅ dz =
Integrando dm desde superficie hasta el tope de la atmósfera se obtiene el valor de
m:
m = Rv
−1
∞
∫
0
e
dz
T
Una masa de 1 kg de agua contenida en una columna de un metro cuadrado de
sección tiene un espesor de 1 mm, con lo cual en la ecuación de arriba m queda
expresada tanto en kg como en mm. Así se define la unidad con la que se suele
expresar a la variable precipitación.
9