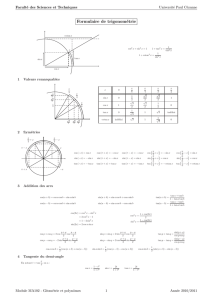
Relations fondamentales Lignes trigonométriques des angles

Relations fondamentales
Formules d’addition des angles
cos(a + b) = cos a cos b − sin a sin b
sin2 t + cos2 t = 1, ∀t ∈ R
tan t =
1
sin t
; 1 + tan2 t =
, ∀t 6=
cos t
cos2 t
(2k+1)π
,
2
cos(a − b) = cos a cos b + sin a sin b
k∈Z
sin(a + b) = sin a cos b + cos a sin b
sin(a − b) = sin a cos b − cos a sin b
Lignes trigonométriques des angles remarquables
t
0
cos t
1
sin t
0
tan t
0
π/6
√
3/2
1/2
√
3/3
π/4
√
2/2
√
2/2
1
π/3
π/2
1/2
√
3/2
√
3
0
tan(a + b) =
tan a + tan b
1 − tan a tan b
tan a − tan b
tan(a − b) =
1 + tan a tan b
1
∞
p+q
p−q
cos
2
2
p−q
p+q
sin
cos p − cos q = −2 sin
2
2
p−q
p+q
cos
sin p + sin q = 2 sin
2
2
p−q
p+q
sin
sin p − sin q = 2 cos
2
2
Symétries et périodicités
cos p + cos q = 2 cos
sin(−t) = − sin t
cos(−t) = cos t
tan(−t) = − tan t
sin(t + 2π) = sin t
cos(t + 2π) = cos t
tan(t + π) = tan t
sin(π − t) = sin t
cos(π − t) = − cos t
tan(π − t) = − tan t
sin(t + π) = − sin t
π
sin t +
= cos t
2
π
− t = cos t
sin
2
cos(t + π) = − cos t
π
cos t +
= − sin t
2
π
− t = sin t
cos
2
tan(t + π) = tan t
π
1
tan t +
=−
2
tan t
1
π
−t =
tan
2
tan t
Formules de multiplication des angles
sin 2a = 2 sin a cos a,
tan 2a =
cos 2a = cos2 a − sin2 a
2 tan a
1 − tan2 a
= 2 cos2 a − 1 ⇒ cos2 a =
1 + cos 2a
2
1 − cos 2a
= 1 − 2 sin a ⇒ sin a =
2
2
2
Cercle trigonométrique et angles remarquables
π/2
2π/3
1
3π/4
O
-1
0
0
C
M
B
sin(t)
1
π/3
π/4
π/6
5π/6
tan(t)
t
cos(t)
P(1,0)
A1
π
-π -1
0
0
0
1
-π/6
-5π/6
-π/4
-3π/4
-1
-2π/3
-1
-π/2
-π/3