EJERCICOS ESTATICA (EQUILIBRIO)
Anuncio

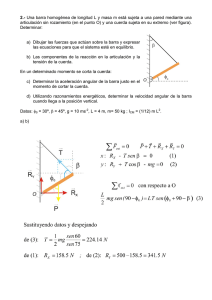
SEQUILIBRIO 1 UNIVERSIDAD DE VALPARAÍSO FACULTAD DE CIENCIAS DEPARTAMENTO DE FÍSICA EQUILIBRIO ESTÁTICO 1.- La barra de la figura de 1[m] de largo y peso despreciable, esta sometida a las fuerzas que se muestran. Encontrar una fuerza "F" y su punto de aplicación de forma que equilibre el sistema 2. F3 = 2[N] F4= 6[N] 20[cm] 30º F5 = 4[N] 80[cm] F1 = 9[N] El tablón de la figura es homogéneo y pesa 1160[N]. Por la escalera de gato sube un Constructor de 900[N] de peso. Calcular la tensión en la cuerda y la reacción en el pivote "A" F2= 8[N] 0.3[m] 37º A B 1.5[m] 3.En la figura siguiente; hállese la tensión T del viento de alambre y las reacciones (vertical y horizontal) sobre el mástil en su extremo inferir A. El mástil mide 3[m] es uniforme y pesa 2500[N]. 10º 55000[N] 60º 4. La pluma de la figura mide 5[m]es homogénea y tiene un peso de 450[N]. Tanto la pluma como la cuerda forman un ángulo de 53,1º con la vertical. La carga que soporta esta constituida por trabajadores de la construcción con peso promedio de "80 Kg." cada uno. ¿Cuántos trabajadores puede levantar la pluma con seguridad, si la tensión de ruptura de la cuerda de la pluma es de 5200[N]. Tome g 10[m/s2] S Maguire 1 53,1º 53,1º 16-11-10 SEQUILIBRIO 2 5. En el dispositivo de la figura. Calcular "m" y las reacciones en "A" 20º 0.75L 0.25L 20º A 500Kg m W = 80[N] 6. Una barra uniforme AB de 1[m] de largo y 20[N] de peso, está unida a una pared por medio de una articulación en A Del otro extremo cuelga una carga de 100[N]. Calcular la fuerza que ejerce el cable CD. Rpta 442[N] D 34º 0.3m A C B 20[N ] 100[N] 7. Una escalera AB de 5[m] de longitud y 30[N] de peso, tiene el centro de gravedad G a 5/3 de su extremo inferior. El suelo es áspero y con roce, mientras que la pared vertical es lisa sin roce. Calcular las reacciones en la pared y en el suelo. Rpta. 7,5[N]; 31[N] 8. La barra AB es uniforme de 4[m] de largo y 50[N] de peso y está articulada en A y sujeta por una cuerda en B. Calcular la tensión en la cuerda y la reacción en A Rpta. 254,5[N], R A = 289[N], 34º 50º B 250(mm) 2m 60º A S Maguire 2 200[N] 2m 16-11-10 SEQUILIBRIO 3 9.- Una estructura de peso despreciable esta sometida a la acción de tres fuerzas, cuyos módulos son: F1 = 30[N] ; F2 = 10[N] , y F3 = 8[N], Ver la figura. Se precisa colocar la estructura en equilibrio aplicando una fuerza “F” en el punto P. Calcular: a) La fuerza “F” aplicada en el punto P (magnitud y dirección) b) La distancia “d” del punto de aplicación de la fuerza “F” respecto del punto O. F1 Rpta. F = 40,8[N] ; d = 1.55[m] F2 b Dirección 78.7º a x P d a a = 4[m] b = 3[m] F3 C 10. – En la figura la barra homogénea AB tiene una longitud de 100[cm] y una masa de 5[Kg].En el equilibrio los ángulos en A y C son de 45º. Si la constante elástica del resorte es de k = 400[N/m]. Calcular su longitud natural. Determine el valor de la masa M que colgada en el punto B, hace que el equilibrio se alcance cuando el ángulo en A sea de 60º. 45º ¿ ? 45º A 11. En la figura el sillín y el marinero en conjunto pesan “w” = 882[N]. Determinar la tensión que soporta los cables OA y OB. Considerar = 60º ; = 30º y g 10[m/s2]. B A S Maguire O 3 16-11-10 B SEQUILIBRIO 4 12.- En los sistemas representados en las siguientes figuras Calcular la tensión T de la cuerda y las reacciones en A. AB= 4m ; BC = 2m T C B wb = 45[kpd] L =2[m] 800[N] T A 60 º 230[kpd] Wb = 50[N] 45º 30ª A 13. Sobre un poste de 5[KN] de peso esta actuando una fuerza F = 8,4[KN] como se indica en la figura. Esta sostenido por una rótula en “A” y por dos cables BD y BE. Determinar la tensión en cada cable y la reacción “A” C 8,4[KN] B 10m 7m D 6m x A 6m 6m z E 14 S Maguire 4 16-11-10