Tabla 1. Método Fundamento y asunciones Ventajas
Anuncio
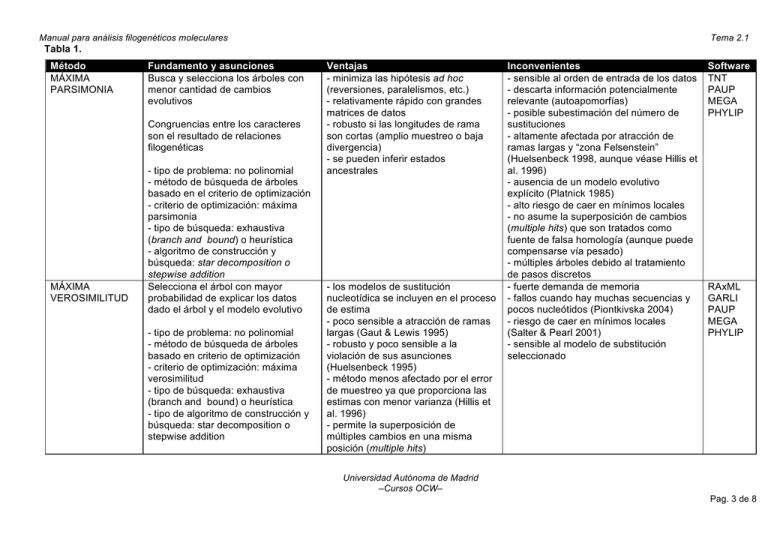
Manual para análisis filogenéticos moleculares Tema 2.1 Tabla 1. Método MÁXIMA PARSIMONIA Fundamento y asunciones Busca y selecciona los árboles con menor cantidad de cambios evolutivos Congruencias entre los caracteres son el resultado de relaciones filogenéticas MÁXIMA VEROSIMILITUD - tipo de problema: no polinomial - método de búsqueda de árboles basado en el criterio de optimización - criterio de optimización: máxima parsimonia - tipo de búsqueda: exhaustiva (branch and bound) o heurística - algoritmo de construcción y búsqueda: star decomposition o stepwise addition Selecciona el árbol con mayor probabilidad de explicar los datos dado el árbol y el modelo evolutivo - tipo de problema: no polinomial - método de búsqueda de árboles basado en criterio de optimización - criterio de optimización: máxima verosimilitud - tipo de búsqueda: exhaustiva (branch and bound) o heurística - tipo de algoritmo de construcción y búsqueda: star decomposition o stepwise addition Ventajas - minimiza las hipótesis ad hoc (reversiones, paralelismos, etc.) - relativamente rápido con grandes matrices de datos - robusto si las longitudes de rama son cortas (amplio muestreo o baja divergencia) - se pueden inferir estados ancestrales - los modelos de sustitución nucleotídica se incluyen en el proceso de estima - poco sensible a atracción de ramas largas (Gaut & Lewis 1995) - robusto y poco sensible a la violación de sus asunciones (Huelsenbeck 1995) - método menos afectado por el error de muestreo ya que proporciona las estimas con menor varianza (Hillis et al. 1996) - permite la superposición de múltiples cambios en una misma posición (multiple hits) Inconvenientes - sensible al orden de entrada de los datos - descarta información potencialmente relevante (autoapomorfías) - posible subestimación del número de sustituciones - altamente afectada por atracción de ramas largas y “zona Felsenstein” (Huelsenbeck 1998, aunque véase Hillis et al. 1996) - ausencia de un modelo evolutivo explícito (Platnick 1985) - alto riesgo de caer en mínimos locales - no asume la superposición de cambios (multiple hits) que son tratados como fuente de falsa homología (aunque puede compensarse vía pesado) - múltiples árboles debido al tratamiento de pasos discretos - fuerte demanda de memoria - fallos cuando hay muchas secuencias y pocos nucleótidos (Piontkivska 2004) - riesgo de caer en mínimos locales (Salter & Pearl 2001) - sensible al modelo de substitución seleccionado Software TNT PAUP MEGA PHYLIP RAxML GARLI PAUP MEGA PHYLIP Universidad Autónoma de Madrid –Cursos OCW– Pag. 3 de 8 Manual para análisis filogenéticos moleculares Tabla 1. [continuación] Método Fundamento y asunciones INFERENCIA BAYESIANA Selecciona los árboles con mayor probabilidad a posteriori de explicar los árboles, dados los datos y el modelo La distribución a priori de los parámetros especificadas - tipo de problema: no polinomial - método de búsqueda de árboles basado en criterio de optimización - criterio de optimización: máxima probabilidad a posteriori - tipo de búsqueda: estocástica - tipo de algoritmo de búsqueda: Metropolis-coupled Markov Chain Monte Carlo NEIGHBOURJOINING Calcula distancias entre pares de especies y devuelve el árbol con menor longitud entre pares de especies y nodos Tema 2.1 Ventajas - los modelos de sustitución nucleotídica se incluyen en el proceso de estima - permite la implementación de modelos evolutivos complejos - relativamente rápido con grandes matrices de datos - poco sensible a atracción de ramas largas - permite la superposición de múltiples cambios en una misma posición (multiple hits) - proporciona valores de apoyo a las ramas - exploran más espacio al usar MCMC - menor riesgo de caer en mínimos locales al usar la variante Metropoliscoupled de MCMC - rapidez - permite la superposición de múltiples cambios en una misma posición (multiple hits) Asume modelo evolutivo - tipo de problema: polinomial - método algorítmico basado en coeficientes de distancias - algoritmo de construcción: star decomposition Inconvenientes - fuerte demanda de memoria - posible sobreestimación de los valores de apoyo de las ramas - sensible al modelo de substitución seleccionado - sensible al orden de entrada de los datos (Farris et al. 1996) - diferencias entre las secuencias no reflejan fielmente la distancia evolutiva - no se pueden identificar los caracteres que apoyan las ramas - pobre para conjuntos grandes de datos - pérdida de información al convertir las secuencias en distancias (Steel et al. 1988) - poco fiables las distancias calculadas cuando las secuencias son altamente divergentes Softwar e MrBayes BAMBE BEAST PHYLIP PAUP MEGA Universidad Autónoma de Madrid –Cursos OCW– Pag. 4 de 8