TEMA 2 Semiconductores - Universidad de Málaga

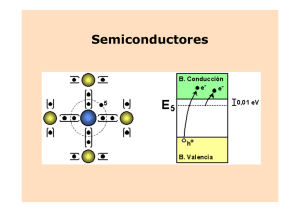
TEMA 2
Semiconductores
TEMA 2.
Semiconductores
ÍNDICE
2.1. CONDUCTORES, SEMICONDUCTORES Y AISLANTES
2.2. ESTRUCTURA CRISTALINA. MODELO DE ENLACE COVALENTE
2.3. CONCEPTO DE PORTADOR. CONCEPTO DE CAMPO ELÉCTRICO
2.4. MOVILIDAD DE PORTADORES POR CAMPO Y POR CONCENTRACIÓN
2.5. MATERIALES INTRÍNSECOS Y EXTRÍNSECOS
2.6. EJERCICIOS RESUELTOS Y PROPUESTOS.
2
TEMA 2.
Semiconductores
OBJETIVOS:
1. Conocer los principios físicos en los que se basa la tecnología
actual de fabricación de circuitos integrados.
2. Conocer los fundamentos de la conducción eléctrica en los
sólidos y las características especiales que presentan los
materiales semiconductores.
BIBLIOGRAFÍA:
1.- Fernández Ramos J. Díaz Lafuente J.L., Romero Sánchez J.
Dispositivos Electrónicos para Estudiantes de Informática.
Universidad de Málaga/Manuales, 2001.
2.- Daza Márquez A., López García J.
'Ejercicios de Dispositivos Electrónicos'.
Universidad de Málaga/Manuales, 2002.
3
TEMA 2.
Semiconductores
2.1. CONDUCTORES, SEMICONDUCTORES Y AISLANTES
La materia está constituida por átomos, con sus electrones distribuidos
en órbitas o capas, cada una de las cuales puede contener un número
máximo permitido de electrones (P. exclusión de Pauli).
La capa más externa con electrones es la capa de valencia y es
determinante para las propiedades eléctricas y químicas de los elementos.
Un electrón en la capa de valencia tiene una energía de la
banda de valencia (Ev)
Para que el electrón escape de la atracción del núcleo, es necesario que
adquiera una energía mínima (Eg) para situarse en la
banda de conducción (Ec). Así,
Eg = Ec - Ev
4
TEMA 2.
Semiconductores
2.1. CONDUCTORES, SEMICONDUCTORES Y AISLANTES
Estructura de bandas de energía.
(a) aislante (b) semiconductor (c ) conductor
5
TEMA 2.
Semiconductores
2.1. CONDUCTORES, SEMICONDUCTORES Y AISLANTES
En un buen aislante, las bandas de valencia y de conducción están muy
separadas. Por tanto, para liberar pocos electrones que contribuyan a la
conducción se necesita gran cantidad de energía. Por ejemplo, el
diamante con Eg ≈ 6 eV.
En un buen conductor, a la temperatura ambiente, las bandas de
valencia y de conducción se solapan. Por tanto, se necesita muy poca
energía para mantener corrientes eléctricas bastante intensas.
Los semiconductores se caracterizan por tener una Eg ≈ 1 eV.
siendo, 1 eV = qV = (1’602x10-19 C). (1 V.) = 1’602x10-19 J.
6
TEMA 2.
Semiconductores
2.2. ESTRUCTURA CRISTALINA. MODELO DE ENLACE COVALENTE
Silicio: Eg = 1.21 eV
Germanio: Eg = 0’785 eV
Silicio: (14 electrones)
1s2 2s2p6 3s2p2
La capa de valencia está incompleta,
debe ganar o perder 4 electrones.
Cuando dos átomos de silicio están próximos, la fuerza de enlace entre
átomos vecinos hace que cada electrón de valencia sea compatible por
uno de sus cuatro vecinos más próximos. ENLACE COVALENTE
7
TEMA 2.
Semiconductores
2.3. CONCEPTO DE PORTADOR. CONCEPTO DE CAMPO ELÉCTRICO
A temperatura ambiente, algunos enlaces covalentes se rompen debido
al suministro de energía térmica al cristal, y es posible la conducción.
Cada enlace covalente roto crea un par electrón-hueco, el electrón con
carga negativa y el hueco con carga positiva (portadores)
Cuando aparece un hueco, el electrón de valencia del átomo vecino deja
su enlace covalente y llena el hueco, esto produce un nuevo hueco. Así,
el hueco se mueve efectivamente en dirección contraria al electrón.
(campo eléctrico)
En un semiconductor puro (intrínseco), el número de huecos (p) es
igual al número de electrones libres (n)
(n=p=ni=pi)
ni, pi son las concentraciones intrínsecas de portadores
8
TEMA 2.
Semiconductores
2.4. MOVILIDAD DE PORTADORES POR CAMPO Y POR CONCENTRACIÓN
El semiconductor en equilibrio, estudiado anteriormente, proporciona un
marco de referencia para el estudio de fenómenos más complejos,
como el movimiento de sus portadores, que ocurren cuando el
semiconductor sale fuera del estado de equilibrio.
Existen tres tipos de causas fundamentales que provocan el movimiento
de los portadores: Arrastre, Difusión y Generación - Recombinación.
Aunque el estudio se hace por separado, estos procesos son simultáneos
dando lugar su estudio a ecuaciones diferenciales que habría que
particularizar para cada caso concreto.
9
TEMA 2.
Semiconductores
2.4.1. FENÓMENOS DE ARRASTRE
Son movimientos de partículas cargadas en respuesta a un campo
eléctrico aplicado.
La fuerza que actúa sobre el portador debido al campo eléctrico acelera
la partícula, aceleración que frecuentemente es interrumpida por los
sucesivos choques con átomos del cristal, aunque el movimiento
neto siempre es en la dirección del campo.
10
TEMA 2.
Semiconductores
2.4.2. FENÓMENOS DE DIFUSIÓN
Difusión es el proceso por el cual los portadores, como consecuencia
del movimiento térmico aleatorio, tienden a redistribuirse desde las
regiones de alta concentración hacia las regiones de baja concentración,
obtiéndose una distribución uniforme de partículas. (Fick)
“Las densidades de corriente de difusión son directamente proporcionales
a los gradientes de concentración” La constante de proporcionalidad se
llama constante de difusión.
Jpd = - q Dp ∇p y Jnd = q Dn ∇n
Considerando simultáneamente los fenómenos de arrastre y difusión,
la densidad de corriente total puede expresarse como sigue:
J = Jp + Jn = Jpa + Jpd + Jna + Jpa =
= q ( p µp + n µn ) E + q ( Dn ∇n - Dp ∇p )
TEMA 2.
Semiconductores
2.4.3. FENÓMENOS DE GENERACIÓN-RECOMBINACIÓN
Generación es el proceso por el cual se crean portadores, y
Recombinación aquel por el cual se destruyen.
En un semiconductor intrínseco (n = p) en equilibrio, la agitación térmica
genera continuamente nuevos pares electrón - hueco y otros pares
desaparecen por recombinación. Si por una causa externa se produce
un incremento de portadores en el cristal, al desaparecer la perturbación
ese incremento va desapareciendo por recombinación hasta lograr
de nuevo el equilibrio. La variación de la concentración de portadores por
ese proceso es directamente proporcional al exceso de portadores
y la constante de proporcionalidad es la inversa del tiempo de vida medio
de dicho portador.
dp / dt = - ∆p / τp y dn / dt = - ∆n / τn
Se define la longitud de difusión (Lp y Ln) de los portadores minoritarios,
como la distancia media que un portador minoritario puede recorrer en un
mar de portadores mayoritarios antes de ser aniquilado por recombinación