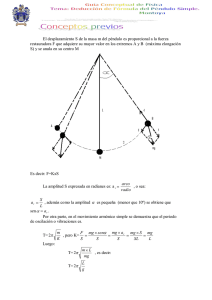
Cálculo de gravedad usando péndulo simple.

Laboratorio de Mecánica, Práctica 4, Equipo 4 (2015)
Cálculo de gravedad usando péndulo simple.
M. E. Martínez Fuentevilla 1, M. Ramírez Torres 1, J. D. Ramos González1, D.
B. Vega Guerrero1, J. A. Villegas Barrientos1.
1Universidad
de Guanajuato, DCNyE
Enviado el 12 de marzo del 2015
RESUMEN
Se obtiene el valor de la gravedad experimentalmente, calculando para ello el
periodo para tres casos diferentes, en los que se emplea una cuerda de diferente
longitud para cada caso. Se hace además una comparación entre los resultados
experimentales encontrados para la aceleración de la gravedad, calculando el
porcentaje de error con respecto al valor de la aceleración real.
1 INTRODUCCIÓN
La longitud del péndulo se mide desde el punto de
suspensión hasta el centro de la esfera. La
amplitud se mide como el desplazamiento
horizontal de la masa con relación al punto de
equilibrio.
El péndulo se empezó a utilizar como instrumento
de medida del tiempo a partir de Galileo.
Apareciendo por esa época las leyes que lo rigen y
que es el motivo de esta práctica. Es de anotar que
a partir de ellas se puede determinar el valor de la
gravedad en un lugar de la tierra.
Si la partícula se desplaza a una posición q0
(ángulo que hace el hilo con la vertical) y luego se
suelta, el péndulo comienza a oscilar.
El péndulo describe una trayectoria circular, un
arco de una circunferencia de radio l.
Las fuerzas que actúan sobre la partícula de masa
m son dos
 El peso mg
 La tensión T del hilo
Medida de la aceleración de la gravedad
Cuando el ángulo q es pequeño entonces, sin q »
q, el péndulo describe oscilaciones armónicas
cuya ecuación es:
q =q0·sen (w t+j)
1
De frecuencia angular w2=g/l, o de periodo
La ley de la gravitación de Newton describe la
fuerza de atracción entre dos cuerpos de masas M
y m respectivamente cuyos centros están
separados una distancia r.
La intensidad del campo gravitatorio g, o la
aceleración de la gravedad en un punto P situado a
una distancia r del centro de un cuerpo celeste de
masa M es la fuerza sobre la unidad de masa
g=F/m colocada en dicho punto.
Su dirección es radial y dirigida hacia el centro del
cuerpo celeste.
2 OBJETIVOS
_Calcular la gravedad tomando el tiempo de
acuerdo al número de oscilaciones con distinto
ángulo y longitud
_Calcular los errores de medición cometidos para
conocer la precisión de dichas mediciones.
Laboratorio de Mecánica, Práctica 4, Equipo 4 (2015)
3 MATERIALES
Se utilizaron los siguientes materiales
experimento:
 Cinta métrica
 Flexómetro
 cronometro
 Una pesa
 Un hilo
 Soporte
para el
4 DESARROLLO EXPERIMENTAL
1.
Armar un sistema fijo en el que una cuerda
amarrada cuelgue y sostenga un objeto de
masa m (péndulo simple).
Figura 2. Se registraba el tiempo que duraban las 15
oscilaciones, para hacer los cálculos previos.
4.
Repetir los pasos anteriores con dos
longitudes de cuerda diferentes y ángulos
despreciables.
5.
Determinar T y T2.
6.
Graficar T2 vs. Longitud del péndulo.
7.
Realizar el ajuste de mínimos cuadrados para
obtener la pendiente.
8.
Obtener g.
5 RESULTADOS
Figura 1. Péndulo en movimiento
2.
Medir con un flexómetro la longitud de la
cuerda.
3.
Soltar el objeto para que empiece a oscilar. Se
cronometrará la duración “t” de 15
oscilaciones completas (ida y vuelta).
2

Primera parte
Laboratorio de Mecánica, Práctica 4, Equipo 4 (2015)

Segunda parte

Tercera parte
Tabla 1. Registro del tiempo para 15 oscilaciones del péndulo, tomando 20
repeticiones para cada longitud diferente de cuerda.
3
Laboratorio de Mecánica, Práctica 4, Equipo 4 (2015)
Prueba 3
T =1.168± . 05
T
0
1.033
1.168
1.331
0
1.067089
1.364224
1.771561
Tabla 2. Datos para graficar
representa al eje x, y
0
23.5
32
41
, en donde l
al eje y.
Para gravedad (g):
Prueba 1
g =8.69±0.1
Prueba 2
g =9.14±0.08
Prueba 3
g =9.26±0.09
Para el % de error:
Prueba 1
Prueba 2
Prueba 3
Figura 3. Gráfica del periodo elevado al cuadrado contra la
longitud, en la que se observa el valor de la pendiente (m).
Utilizando la información que nos proporciona la
gráfica se calcula el valor de la aceleración de la
gravedad utilizando la siguiente fórmula:
6 CONCLUSIONES
Las mediciones fueron tomadas lo más exactas
posibles, por ende obtuvimos buenos resultados en
los cálculos. Además de que los errores para el
periodo y la gravedad fueron relativamente bajos.
Para periodo (T):
Prueba 1
T =1.033± . 07
Prueba 2
T =1.331± . 05
4
Todo esto nos hace concluir que las mediciones
fueron relativamente buenas y nuestra gravedad
solo se aleja poco del valor real.
7 BIBLIOGRAFÍA

Página web, EL péndulo simple. Dinámica
[en línea]. [Fecha de consulta: 10 marzo de
2015].
http://www.sc.ehu.es/sbweb/fisica/dinamica
/trabajo/pendulo/pendulo.htm