FÍSICA NUCLEAR

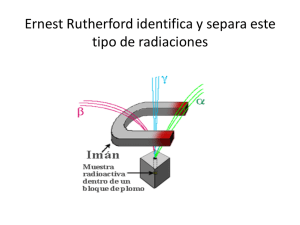
ELEMENTOS BÁSICOS DE FÍSICA NUCLEAR
FELIPE MORENO ROMERO
LCDO. CIENCIAS QUÍMICAS
(JUNIO, 2007)
Contenidos:
1.- Composición del núcleo. Isótopos.
2.- Estabilidad de los núcleos. Energía de enlace.
3.- Radiactividad.
4.- Reacciones nucleares.
۞۞۞۞
El inicio de la física nuclear se puede establecer en 1896 con el descubrimiento de la
radiactividad por parte de Henri Becquerel.
Becquerel estudiaba por entonces la luz emitida por algunas sustancias, llamada
fluorescencia. Una de estas sustancias fluorescentes es el sulfato de potasio y uranilo: UO2KSO4.
La fluorescencia es la propiedad de una sustancia para emitir luz cuando es expuesta a
radiaciones del tipo ultravioleta, rayos catódicos o rayos X. Las radiaciones absorbidas (invisibles
al ojo humano), son transformadas en luz visible, o sea, de una longitud de onda mayor a la
incidente. Un día que estaba nublado no permitía a Becquerel exponer el sulfato de potasio y
uranilo a las radiaciones del Sol así que las guardó en un cajón en el que también tenía unas
placas fotográficas sin velar (protegidas con un grueso papel negro para que no se velaran al
darles la luz). Días más tarde comprobó que la película fotográfica de estas placas estaba velada
cuando “en teoría” no había sido expuesta a ningún tipo de luz. Becquerel pensó que la sal de
uranilo emitía algún tipo de radiación invisible capaz de velar la placa fotográfica. A partir de este
descubrimiento casual comprobó que otros compuestos de uranio también velaban las placas
fotográficas, llamando a esa radiación invisible radiactividad.
-1-
Dos años más tarde Pierre y Marie Curie descubrieron otros dos elementos nuevos en la
tabla periódica, el polonio y el radio, ambos radiactivos.
La física nuclear estudia el comportamiento de los núcleos atómicos.
1.- Composición del núcleo. Isótopos
El átomo es básicamente vacío tal como descubrió E. Rutherford en 1911 a partir de su
famosa experiencia (esquematizada en la figura adjunta).
El polonio es una fuente
radiactiva de partículas α (partículas
cargadas positivamente).El haz de
partículas se hace incidir sobre una
fina lámina de oro de forma que se
observa que la mayoría de ellas
atraviesa dicha lámina y son
detectadas en una pantalla de
sulfuro de zinc en forma de un
centelleo en el momento en que una
partícula
incide
sobre
dicha
pantalla. No obstante Rutherford
observó que algunas partículas eran
desviadas y que incluso algunas salían rebotadas de la lámina de oro.
A partir de esta experiencia Rutherford estableció junto a
sus colaboradores (Geiger y Mariden) su conocido modelo
atómico. Este modelo permitía explicar los resultados del
experimento tal como se muestra en la figura adjunta. Las flechas
negras indican la trayectoria de las partículas α: el primer caso se
trataría del modelo atómico anterior de Thomson, el segundo caso
es el modelo de Rutherford.
Actualmente sabemos que el núcleo atómico contiene dos
tipos de partículas, los protones (de carga positiva e igual en valor,
cada uno, a la carga elemental del electrón) y los neutrones, sin
carga y de masa aproximadamente igual a la de los protones
aunque un poco superior. Los neutrones no fueron descubiertos
realmente hasta 1932 aunque su existencia se sospechaba con
anterioridad.
Las características básicas de las tres partículas atómicas fundamentales son:
Partícula
Masa (kg)
Masa (u.m.a.)
Carga (C)
Ubicación
Protón
1’6726 · 10-27
1’0073
1’6 · 10-19
Núcleo
Neutrón
1’675 · 10-27
1’0087
0
Núcleo
Electrón
9’1 · 10-31
0’00055
1’6 · 10-19
Corteza
-2-
Conceptos necesarios
La masa del electrón es 1836 veces menor a la del protón. En general se llaman nucleones a
las partículas que hay en el núcleo (protones o neutrones), y núclido a cada especie nuclear de un
elemento químico. El número atómico (Z) es el número de protones que hay en el núcleo,
coincide con el número de electrones de la periferia para el átomo neutro y es el que define al
elemento químico como tal. A la suma del número de protones (Z) y del número de neutrones (N)
de un núcleo se le llama número másico (A):
A=Z+N
Para simbolizar un átomo, por ejemplo el elemento general X, se sigue el siguiente criterio
en cuanto a la disposición de estos números:
A
Z
por ejemplo: 37 Li,
Li  ,
7
3
1
1
H,
13
6
C,
X C arg a
235
92
U . Normalmente el número atómico se suele obviar.
Isótopos son átomos de un mismo elemento que tienen distinto número de neutrones. Los
más “famosos” entre ellos tienen nombre específico: son los isótopos del hidrógeno,
1
1
H
Hidrógeno (un único protón y un
electrón)
2
1
H
Deuterio (también “D”)
3
1
H
Tritio (también “T”)
Los demás isótopos no tienen un nombre establecido. Para nombrarlos se hace mención al
número másico correspondiente. Por ejemplo, el carbono tiene tres isótopos, el carbono-12, el
carbono-13 y el carbono-14, éste último radiactivo:
12
6
C,
13
6
C,
14
6
C
Proporciones isotópicas en la naturaleza
En una sustancia pura hay siempre varios isótopos (la mayoría estables y, en algunos casos,
alguno radiactivo). Por ejemplo, si tenemos un kilogramo del elemento cloro sabemos que estará
formado por átomos de dicho elemento del que existen dos isótopos: el cloro-35 y el cloro-37. La
proporción de cada uno determina el peso atómico que aparece en la tabla periódica ya que este
es en realidad el peso atómico medio de los diferentes isótopos naturales que lo forman. Si el 50%
de todo el cloro fuera cloro-35 y el otro 50% fuera cloro-37, el peso atómico del cloro sería 36
u.m.a., pero resulta que es en realidad 35’45 u.m.a., es decir, hay una mayoría de cloro-35 frente a
cloro-37. Para conocer dicha proporción exacta debemos resolver la ecuación:
35x  37(1  x)  35'45
donde x es el tanto por uno de cloro-35 y 1-x es el tanto por uno de cloro 37. Si resolvemos
obtendremos que x = 0’754, es decir, hay un 75’4% de cloro-35 y un 24’6% de cloro-37.
-3-
Este procedimiento de cálculo es similar para otros elementos aunque se complicará un
poco la ecuación si en la naturaleza son posibles más de dos isótopos para un elemento. Habría
que recurrir a sistemas de ecuaciones.
Unidad de masa atómica
Se ha utilizado ya en estos apuntes la unidad de masa atómica, u.m.a. o simplemente “u”,
para designar la masa de un átomo. Dado que la masa de los electrones es despreciable, la masa
de un átomo es en realidad la masa de su núcleo. Pero como esta masa en kilogramos es muy
pequeña, se utiliza la u.m.a.
Actualmente (no siempre ha sido así) se ha consensuado que la unidad e masa atómica sea
la doceava parte de la masa del isótopo carbono-12. En base a esta unidad decidida están
expresados lo pesos atómicos que aparecen en la tabla periódica (mejor debería ser “masas
atómicas” aunque en estos apuntes se utilizarán los dos nombres indistintamente).
Problema:
Calcular la energía que corresponde a 1 u.
Solución:
Si buscamos la masa atómica del carbono vemos que es de 12 u, es decir, 12 gramos de carbono-12
contienen 6’023 · 1023 átomos del elemento (nº de Avogadro). Con un simple cálculo podemos conocer la masa de
un átomo de carbono-12:
12
 1'99 ·10 23 g  1'99 ·10 26 kg
23
6'023 ·10
1 u.m.a es la doceava parte de esta masa, es decir: 1’66 · 10-27 kg.
La energía que corresponde a esta masa se puede conocer con la ecuación de Einstein:
E  mc2  1'66 ·10-27 · (3 ·108 ) 2  1'49 ·10-10 J  9'34 ·108 eV  934 MeV
El equivalente energético de la unidad de masa atómica calculado más exactamente 1 es de 931 MeV
2.- Estabilidad de los núcleos. Energía de enlace.
El tamaño de un núcleo atómico obedece aproximadamente la siguiente expresión:
R  1'2 ·1015· A1/ 3
por ejemplo, para el carbono-12:
R  1'2·1015·3 12  2'7·1015 m
1
1 u · c2 = (1.66054 × 10-27 kg) × (2.99792 × 108 m/s)2
= 1.49242 × 10-10 kg (m/s)2 = 1.49242 × 10-10 J
× (1 MeV / 1.60218 × 10-13 J)
= 931.49 MeV,
-4-
Si suponemos que el núcleo es esférico, podemos determinar la densidad del mismo:
d
m 12 ·1'66 ·10 27

 2'29·1017 kg / m3
4
V
R 3
3
Un valor bastante elevado por cierto. ¿Cómo pueden permanecer juntos los protones en el
núcleo si éstos se repelen eléctricamente y más aún cuando la distancia entre dos protones es tan
“grande” como 10-15 m (= 1 fermi). Si quisiéramos determinar el valor de la fuerza de repulsión
eléctrica según la ley de Coulomb veríamos que
FK
-19 2
q1q2
)
9 (1'6 ·10

9
·
10
 230 N
2
15 2
d
(10 )
esta fuerza provocaría una aceleración en el protón de
a
F
230

 1'37 ·1039 m / s 2
-27
m 1'673 ·10
es decir, una exageración.
Debe existir una fuerza que a nivel nuclear sea más intensa que la repulsión eléctrica entre
los protones y que sea la responsable de que los protones se mantengan unidos en el núcleo. Esta
interacción se llama nuclear fuerte y es también responsable de que los neutrones (partículas sin
carga y, por tanto, sin necesidad de estar en el núcleo pues la fuerza gravitatoria es mínima)
permanezcan también fuertemente ligadas en el núcleo. Cuatro características básicas que
resumen la interacción nuclear fuerte son:
- Sólo se manifiesta en el interior del núcleo, es decir su alcance es de un fermi.
- Es la más intensa de todas las interacciones conocidas (gravitatoria, electromagnética y
nuclear débil de la que se hablará más adelante). Concretamente es 100 veces superior a la
electromagnética que es la segunda interacción más intensa.
- Sólo se manifiesta entre dos protones, entre dos neutrones o entre un protón y un
neutrón.
- Es de carácter atractivo.
Defecto de masa
Cuando nos planteamos la cuestión de pesar un núcleo atómico tenemos dos opciones:
1ª) Cálculo teórico: determino el número de protones que tiene y lo multiplico por la masa
del protón. Determino el número de neutrones que tiene y lo multiplico por la masa del neutrón.
Finalmente sumo las dos cantidades obtenidas.
2ª) Determinación experimental: utilizando un espectrómetro de masas (ver apéndice).
El valor obtenido experimentalmente es siempre menor al obtenido de forma teórica. De
hecho, si ocurriera al revés el núcleo no sería estable, no existiría. A este defecto entre la masa
-5-
calculada de forma teórica y la masa determinada experimentalmente se le denomina defecto de
masa y se puede determinar (en u.m.a.) según la siguiente expresión:
m  Zmp  ( A  Z )mn  M
donde Z es el número atómico, mp es la masa del protón, A-Z es el número de neutrones, mn es la
masa del neutrón y M es la masa del núcleo determinada experimentalmente.
Este defecto de masa equivale a energía:
E  mc2
que se denomina energía de enlace del núcleo. Es la energía que se libera cuando los nucleones
constituyentes del núcleo se unen (desde el infinito) para formar el núcleo o, también, la energía
necesaria para romper el núcleo totalmente.
Las energías de enlace de los núcleos son enormes, oscilan entre 2’2 MeV para el deuterio
2
1
( H ) y 1640 MeV para el isótopo
209
83
Bi . Tengamos en cuenta que un kilogramo de gasolina tiene
una energía interna de 4’6 · 104 kJ y que un kilogramo de núcleos, por término medio, desprenden
al formarse 1012 kJ, es decir, unas veinte millones de veces más energía. Todos sabemos lo que se
puede hacer con un kilo de gasolina.
En lugar de energía de enlace del núcleo se suele hablar de energía de enlace por nucleón,
que se obtiene de dividir la primera entre el número de nucleones que tiene el núcleo
considerado.
La
gráfica
siguiente
representa cómo varía esta energía de
enlace por nucleón (ΔE/A) con respecto al
número másico (A) para los diferentes
isótopos conocidos.
Se puede observar que cuanto
mayor es la energía de enlace por nucleón
más estable es el núcleo, no obstante a
partir del hierro esta energía empieza a
disminuir paulatinamente. El núcleo más
estable es el hierro-56. al que corresponde
una energía
de enlace
de 8’8
MeV/nucleón. Las mayores energías de
enlace por nucleón se presentan para números másicos comprendidos entre 40 y 100
aproximadamente.
Si un núcleo pesado se divide en dos núcleos más ligeros (fisión nuclear), o si dos núcleos
ligeros se unen para formar uno más pesado (fusión nuclear), se obtienen núcleos más estables, es
decir, con mayor energía de enlace por nucleón entre los productos de la reacción nuclear que la
que tenían el o los núcleos de partida.
Problema:
Determina el defecto de masa, la energía de enlace y la energía de enlace por nucleón para el núcleo de carbono-12.
Solución:
-6-
El defecto de masa de un núcleo es la diferencia entre la masa de sus constituyentes y la masa real del núcleo.
Como el número atómico del carbono es Z=6, su núcleo está formado por seis protones y seis neutrones. La masa
total de estas partículas es la siguiente:
Masa de 6 protones = 6 · 1’0073 u
=
6’0438 u
Masa de 6 neutrones = 6 · 1’0087 u
=
6’0522 u
Masa total . . . . . . . . . . . . . . . . . . . . . . .
12’0960 u
Masa del núcleo de carbono-12
=
12’0000 u
Defecto de masa . . . . . . . . . . . . . . . . . .
0’0960 u
Como 1 u equivale a 931 MeV, la energía de enlace será:
E = 0’096 u · 931 MeV/u = 89’4 MeV
El núcleo de carbono-12 está formado por 12 nucleones, en consecuencia, la energía de enlace por nucleón es:
E
89'4 MeV

 7'4 MeV / nucleón
A 12 nucleones
3.- Radiactividad.
Todos los núcleos atómicos son susceptibles de desintegrarse más o menos lentamente. El
núcleo de hierro-56 que es el más estable también se puede desintegrar aunque lo hace muy, muy
lentamente. De todos los isótopos conocidos se dice que son estables aquellos que no se
desintegran o permanecen sin desintegrarse durante muchos miles de años.
Los núcleos inestables se desintegran convirtiéndose en otros núcleos que pueden ser a su
vez estables o no. Desde que se formó la Tierra han desaparecido muchos núcleos inestables que
se han transformado en otros estables: son los más rápidos en desintegrarse, pero aún quedan
núcleos que se están desintegrando. A estos elementos que todavía quedan, inestables, se les
llama elementos radiactivos naturales. También se han sintetizado en laboratorio o en centrales
nucleares elementos inestables, llamados radiactivos artificiales.
El primer elemento radiactivo natural encontrado fue el uranio por Henri Becquerel en
1896. Dos años más tarde los esposos Curie descubrieron el radio y el polonio.
Se llaman elementos radiactivos porque en un primer momento se creía que emitían rayos
cuya naturaleza no se conocía, pero que eran capaces de velar placas fotográficas. Este nombre ha
permanecido aunque posteriormente se ha comprobado que la “radiación” que emiten son en
realidad partículas en su mayor parte.
En la radiactividad natural se pueden encontrar tres tipos diferentes de emisiones
radiactivas (también tres tipos de radiaciones):
Radiación α:
Consiste en la emisión por parte del núcleo inestable de una partícula α, es decir de un
núcleo de helio-4:
-7-
partícula   24He2
Esta partícula suele ser emitida por núcleos grandes (uranio, torio, radio, plutonio….). La
explicación de esta emisión es la siguiente: en los núcleos pequeños se observa que el número de
protones es aproximadamente igual al número de neutrones, pero en núcleos mayores (estables)
el número de neutrones es mayor al de protones
para compensar la repulsión electrostática
creciente debido al aumento de cargas positivas
en el núcleo. En la gráfica adjunta se han
representado el número de neutrones de los
núcleos estables frente al número de protones
de los mismos. Se puede observar que la
igualdad entre el número de protones y
neutrones en un núcleo atómico estable se
mantiene para números atómicos inferiores a 30
y a partir de entonces se desvía de esa tendencia
cada vez más.
Cuando los núcleos son muy grandes llega
un momento en que el exceso de protones es
grande, las repulsiones eléctricas entre ellos son tan grandes que ya ni un exceso de neutrones
puede compensar y el núcleo “simplemente se deshace de 2 protones y dos neutrones”
emitiéndolos en forma de partícula α. Por ejemplo, el radio descubierto por el matrimonio Curie
contiene un isótopo, el radio-226, que es un emisor α según la siguiente reacción:
226
88
Ra

He2
Rn 
222
86
4
2
vemos que la el radio, al perder dos electrones pasa a tener número atómico 86, es decir, pasa a
ser radón. Como también se han perdido dos neutrones el número másico se ha reducido en 4
unidades, se trata del isótopo radón-222. Se observa en la reacción anterior, que podemos llamar
reacción nuclear, se debe conservar en todo momento la carga total (protones) y el número de
nucleones.
El descubrimiento en 1913 de las leyes que regulan el desplazamiento en las
transformaciones radiactivas se debe a K. Fajans y a R. Soddy y llevan el nombre de leyes de
Fajans-Soddy. Para el caso de la emisión α hemos visto que cuando un núcleo emite una partícula
α, el nuevo núcleo disminuye en 4 unidades sus nucleones y en dos unidades sus protones. En
general:
A
Z
X

A- 4
Z-2
Y

He2
4
2
La partícula α es relativamente pesada y su carga eléctrica (2+) la hace interaccionar
rápidamente con el entorno; ello hace que sea emitida a velocidades no muy altas. La partícula α
tiene un poder de penetración muy pequeño, siendo detenida por una lámina de cartón o unos
pocos centímetros de aire. No es capaz de atravesar la piel de nuestro cuerpo. No obstante, es
peligrosa por ingestión de un emisor α (o por respiración de polvo radiactivo) ya que en el interior
del cuerpo, durante su corto trayecto produce ionizaciones locales y alteraciones químicas muy
importantes.
-8-
Radiación β:
Consiste en la emisión, por parte del núcleo, de una partícula β y de un neutrino (ν). La
partícula β es en realidad un electrón rápido y el neutrino es una partícula neutra y de masa
despreciable. Para las pretensiones de estos apuntes, el neutrino no se tendrá en cuenta.
Se suele producir cuando la relación A-Z/Z es demasiado grande, entonces en el núcleo un
neutrón se transforma en un protón:
1
0
n 
p 
1
1
0
1
e
Esta es la explicación de que un núcleo emita electrones. ¿Cómo es posible que de un
núcleo atómico se emitan electrones? Acabamos de ver que lo que en realidad ocurre es que uno
de los neutrones del núcleo, de carga nula, se divide en dos partículas, un protón y un electrón (la
carga neta sigue siendo nula). Por ejemplo, el isótopo carbono-14 es un emisor β, circunstancia
que se puede aprovechar para datar la antigüedad de restos fósiles. La reacción de desintegración
correspondiente sería:
C 
14
6
N 
14
7
0
-1
e
por curiosidad vemos que en este ejemplo la relación A-Z/Z es 8/6 = 1’3. Otro ejemplo de emisor β
es el bismuto-214:
Bi 
214
83
Po 
214
84
0
-1
e
La ley de Fajans y Soddy para la emisión β establece, por tanto, que cuando un núcleo emite
una partícula β, se transforma en un nuevo núcleo cuyo número de protones ha aumentado en
una unidad y sus nucleones no han variado, en general
A
Z
X 
Y 
A
Z 1
0
-1
e
Las partículas β se emiten con velocidades próximas a la de la luz, su masa es mucho menor
que la de las partículas α y, por tanto, su poder de penetración en mucho mayor. Son frenadas por
unos metros de aire, una lámina de aluminio o unos centímetros de agua. Podemos imaginar que
el material que frena una partícula radiactiva no es indicativo de su peligrosidad; sí lo es lo que la
partícula puede hacer mientras está siendo frenada.
Radiación γ:
En este caso sí se trata de una radiación propiamente dicha ya que en los dos casos
anteriores son partículas concretas. Por tanto, se trata de ondas electromagnéticas emitidas por
los núcleos radiactivos cuya longitud de onda es muy pequeña siendo, por tanto, muy energéticas.
La radiación γ acompaña generalmente o a la emisión α o a la emisión β ya que el núcleo
que emite estas partículas queda en un estado excitado de energía. Vuelve a su nivel o estado
-9-
fundamental emitiendo energía en forma de cuantos de radiación γ. Por tanto, una emisión γ no
cambia la naturaleza de la especie que la emite.
El poder de penetración de los rayos γ es considerablemente mayor al de las partículas α ó
β. Atraviesan el cuerpo humano y sólo se frenan con planchas de plomo y muros gruesos de
hormigón. La radiación γ es muy peligrosa para la vida en general.
Ley de la desintegración radiactiva.
Los tres tipos de radiactividad mencionados aquí son los que se presentan en los núcleos
radiactivos naturales. No son, sin embargo, los únicos tipos de radiactividad. En núcleos
radiactivos artificiales se han observado otros tipos de emisiones radiactivas como la
desintegración β+ o la captura electrónica. El estudio de las características de estas emisiones se
aleja de las pretensiones de estos apuntes aunque se puede decir que toda emisión radiactiva
(natural o artificial) sigue una ley conocida como ley de la desintegración radiactiva.
En 1900 Rutherford sugirió que el ritmo de emisión radiactiva de una sustancia disminuye
exponencialmente con el tiempo. Los procesos radiactivos son aleatorios, han de estudiarse
estadísticamente, basando las deducciones en el cálculo de probabilidades: de probabilidad de
que un núcleo concreto se desintegre en un instante concreto.
Para ver cómo es este estudio imaginemos una muestra con N0 núcleos radiactivos en el
tiempo t0. Cuando pase un tiempo t , parte de los núcleos se han desintegrado y quedan
concretamente N núcleos radiactivos (N<N0).
La velocidad de desintegración será el ritmo de cambio del número de núcleos radiactivos
en función del tiempo transcurrido, es decir:
velocidad de desintegra ción 
N - N 0 N

t - t0
t
Se puede comprobar (Rutherford y Soddy, 1902) que esta velocidad es proporcional al
número de núcleos existentes, es decir:
N
  N
t
donde λ es llamada constante de desintegración, característica de cada núcleo y cuyas unidades
son, en el S.I., s-1 (aunque no debemos confundirla con la unidad de frecuencia). El signo menos
de la ecuación anterior indica que el número de núcleos disminuye con el tiempo.
- 10 -
Si reordenamos la ecuación y consideramos intervalos de tiempo infinitesimales, los
incrementos pasan a diferenciales:
N
 t
N

dN
 dt
N
Si queremos conocer el número de núcleos (N) que quedan después de un tiempo (t),
siendo N0 el número de núcleos al principio, debemos integrar

dN
  dt
N 
ln
N
 t
N0
N  N 0e  t
Las dos últimas ecuaciones son dos formas de
expresar la ley de desintegración radiactiva. Es una
expresión general aplicable a cualquier desintegración
radiactiva. La representación gráfica de la última ecuación
nos da una idea de cómo va disminuyendo el número de
núcleos radiactivos desde una cantidad inicial para tiempo
cero (figura adjunta)
Otros términos o conceptos muy utilizados en el
análisis de la desintegración radiactiva son 3:
1- Actividad o velocidad de desintegración: es la
velocidad de desintegración, es decir el número de emisiones de una sustancia por unidad de
tiempo. Su unidad en el S.I. es el becquerel (Bq), que es una desintegración por segundo. Por
tanto:
A
dN
 N  N 0 e  t  A0 e  t , donde A0  N 0 es la actividad en el instante inicial
dt
2- Periodo de semidesintegración: o periodo de semivida (T1/2), es el tiempo que tiene que
transcurrir para que el número de átomos radiactivos de una muestra determinada baje a la
mitad. Apliquemos esta definición en la ley de desintegración radiactiva:
N0
 N 0 e  T1/2
2
1
 e  T1/2
2
ln
1
 T1/ 2 ln e
2
- 11 -
 0'693  T1/ 2
T1/ 2 
0'693


ln 2

A modo de ejemplo, en la tabla siguiente aparecen los periodos de semidesintegración de
algunos núcleos radiactivos.
Berilio-8
Polonio-213
-16
4 · 10 s
10
s
-6
Aluminio28
Yodo-131
Estroncio90
Radio-226
Carbono-14
Rubidio-87
2’25 min.
8 días
28 años
1600 años
5730 años
5’7 · 10
años
10
3- Vida media (τ): es el promedio de vida o tiempo que, por término medio, tarda un núcleo
en desintegrarse. Es la inversa de la constante de desintegración:

1


T1/ 2
ln 2
Problema
En una muestra de madera de un sarcófago ocurren 13536 desintegraciones en un día por cada gramo, debido al 14C
presente, mientras que una muestra actual de madera análoga experimenta 920 desintegraciones por gramo en una
hora. El período de semidesintegración del 14C es de 5730 años.
a) Establezca la edad del sarcófago.
b) Determine la actividad de la muestra del sarcófago dentro de 1000 años.
Solución
a) Hay que pasar los dos datos de actividad a desintegraciones por segundo. En ambos casos el dato ofrecido es por
gramo de muestra, por tanto, en el caso de la muestra del sarcófago:
A  13536
desintegra ciones
1 día
desintegra ciones
x
 0'157
día
86400 segundos
segundo
Para el caso de la muestra actual la actividad se puede considerar como actividad en el instante inicial pues es un
trozo de madera es de las mismas características a la del sarcófago:
A0  920
desintegra ciones
1 hora
desintegra ciones
x
 0'256
hora
3600 segundos
segundo
Por otra parte, con el dato de T1/2 podemos conocer la constante de desintegración del carbono-14:
T1/ 2  5730 años  1'81·1011 s 
ln 2

;
  3'83 ·10-12 s 1
De la expresión de la actividad todo es conocido y podemos obtener el tiempo transcurrido:
A  A0 e  t ;
A
A
0'157
 e  t ; ln
  t ; ln
 3'83 ·10-12 t
A0
A0
0'256
t = 1’276 · 1011 s = 4045 años.
b) Dentro de 1000 años (1000 x 365’25 x 86400 = 3’156 · 107 s) el sarcófago tendrá una antigüedad de 5045 años
(1’592 · 1011 s). Su actividad será de
- 12 -
A  0'256 e( 3'83·10
-12
·1'592·10 11)
 0'139 desintegra ciones por segundo y por gramo
Problema
Una muestra de una sustancia radiactiva de 0’8 kg se desintegra de tal manera que, al cabo de 20 horas, su
actividad se ha reducido a la cuarta parte. Calcule el periodo de semidesintegración.
Solución
En primer lugar, 20 horas son 20 · 3600 = 72000 segundos.
La actividad inicial de la muestra se debe a los 0’8 kg de sustancia radiactiva que hay al principio.
En 20 horas dicha actividad ha bajado a la cuarta parte según informa el enunciado del problema. Por tanto, la
cantidad de muestra se debe haber reducido a la cuarta parte de la inicial:
-
Al cabo de 72000 s, A = A0/4 = 0’25·Ao
-
Cantidad de sustancia radiactiva que queda = 0’8/4 = 0’2 kg
No obstante, la cantidad de muestra no es necesaria para resolver el problema:
A  A0 e  t ;
0'25A0
 e  t ; ln 0'25   · 72000 ;   1'925 ·10-5 s 1
A0
Tenemos ahora los datos necesarios para calcular T1/2:
T1/ 2 
ln 2

 36000 s
Problema
Tenemos 70 gramos del isótopo radiactivo cromo-51 (artificial), con un periodo de semidesintegración de 27 días.
¿Cuántos átomos quedarán de dicho isótopo al cabo de seis meses?
Solución
Con el dato del periodo de semidesintegración obtenemos la constante de desintegración del cromo-51:
T1/ 2  27 días  2'33 · 106 s 
ln 2

;
  2'97 ·10-7 s 1
Por otra parte, 70 gramos de cromo-51 son
70 g ·
1 mol
átomos
· 6'023 ·10 23
 8'27 ·10 23 átomos
51 g
mol
Tenemos ya todos los datos necesarios para calcular el número de átomos que quedarán al cabo de seis meses (6 x
10 x 86400 = 1’56 · 107 s)
N  N 0e  t  8'27 ·1023 · e( 2'97 ·10
-7
·1'56·10 7 )
 8'04 ·1021 átomos
Familias radiactivas
Si el periodo de semidesintegración del radio es de sólo 1600 años, ¿cómo es posible que
fuera descubierto en la pechblenda (mineral de uranio) por el matrimonio Curie si la edad de la
Tierra es lo suficientemente grande como para que ya no hubiera ni rastro de elemento?
- 13 -
Se puede comprobar que con ese periodo de semidesintegración, de una muestra inicial en
la tierra de N0 átomos de radio, en 4500 millones de años, el número de átomos habría bajado en
un 99’999982%, es decir, sería indetectable. Marie y Pierre Curie procesaron varias toneladas de
pechblenda para obtener un gramo de radio, pero con el porcentaje calculado la cantidad debería
haber sido mucho mayor.
La respuesta está en que el radio-226 que
actualmente hay en la pechblenda es un núcleo
resultado de una desintegración radiactiva del
torio-230 que a su vez procede de la
desintegración radiactiva del uranio-234, que a su
vez procede de la desintegración radiactiva del
protoactino-234, que a su vez procede de la
desintegración radiactiva del torio-234 que, por
fin, procede de la desintegración radiactiva del
uranio-238. El radio-226 va apareciendo en el
mineral a medida que se van desintegrando sus
“progenitores”. El primero de la lista, el uranio238, tiene un periodo de semidesintegración de
4’51 · 109 años, lo suficientemente grande como
para ser responsable de que todavía exista el
radio-226.
Una serie radiactiva, también familia
radiactiva, es una serie encadenada de
desintegraciones radiactivas que desembocan en
un núcleo estable no radiactivo. En la naturaleza
hay 4 series radiactivas que se nombran
atendiendo al núcleo que empieza la serie. Existen
además un gran número de series radiactivas
artificiales.
En la figura adjunta, a modo de ejemplo, aparece la serie radiactiva del Uranio-238. En la
tabla siguiente aparecen las características más relevantes de las cuatro series radiactivas
naturales.
Serie
Nº másico
Núcleo padre
T1/2
Núcleo final
Torio
4n
Torio-232
1’39 · 1010 años
plomo-208
Neptunio
4n+1
Neptunio-237
2’25 · 106 años
bismuto-209
Uranio
4n+2
Uranio-238
4’51 · 109 años
plomo-206
Uranio - Actinio
4n+3
Uranio-235
7’07 · 108 años
plomo-207
La columna del número másico significa que todos los números másicos de los núcleos de
cada serie responden a esa expresión siendo n u número entero.
- 14 -
El periodo de semidesintegración del neptunio no es lo suficientemente grande como para
que este núcleo exista en cantidades “apreciables” a no ser que se busque en una gran cantidad de
mineral, sin embargo el actinio-89 que forma parte de esta serie si tiene un periodo de
semidesintegración alto.
4.- Reacciones nucleares.
Una reacción nuclear es un proceso de combinación y transformación de las partículas y
núcleos atómicos. Una reacción nuclear se representa mediante una ecuación que muestra el
proceso en el que intervienen núcleos atómicos. Ya se han visto a lo largo de estos apuntes
algunas reacciones referentes a procesos radiactivos ya que la desintegración α y β pueden
considerarse como reacciones nucleares. Existen otro tipo de reacciones nucleares consistentes en
el bombardeo de un núcleo con otros núcleos de menor tamaño o, incluso, con partículas
subatómicas.
La primera reacción nuclear (diferente a la desintegración radiactiva) estudiada lo fue por
parte de Rutherford en 1919: consiste en el bombardeo de núcleos de nitrógeno-14 con partículas α
(procedentes de la desintegración del radio-226):
14
7
N 
He 
O 
4
2
17
8
1
1
p
Podemos pensar que el sueño de los alquimistas está cerca pues el nitrógeno se ha
convertido en oxígeno de forma artificial. Otro ejemplo de reacción nuclear, utilizada por IreneJoliot Curie (hija de Marie y Pierre Curie) y su esposo Jean Fréderic Joliot-Curie les permitió
descubrir la radiactividad artificial:
27
13
Al 
He 
P 
4
2
30
15
1
0
n
el fósforo-30 es radiactivo, fue el primer isótopo radiactivo sintetizado en un laboratorio y
permitió al matrimonio descubridor recibir el premio Nobel en 1935.
Podemos ver en la última reacción nuclear un motivo del porqué de la peligrosidad de la
partícula α ya que produce reacciones nucleares que dan lugar a nuevos núcleos radiactivos.
Más ejemplos:
7
3
Li 
27
13
Al 
p 
1
1
n 
1
0
He 
4
2
4
2
Mg 
27
12
He
1
1
p
Podemos ver en todas estas reacciones que se debe conservar la masa (la suma de los
números másicos de los productos y reactivos es la misma) y la carga (la suma de los números
atómicos –protones- en productos y reactivos es la misma).
El catálogo de partículas y núcleos utilizados para bombardear es muy extenso. Las más
importantes, junto con sus símbolos, son:
Partícula α, 24 He
Protón, 11 p ó
- 15 -
1
1
H
Deuterio, 12 H
Electrón,
0
1
Neutrón, 01 n
e
Las partículas con carga eléctrica se pueden acelerar con campos eléctricos y magnéticos
con el objeto de facilitar el choque y la reacción (aceleradores de partículas) al impactar a gran
velocidad con el blanco. El neutrón y otras partículas neutras no se pueden acelerar dado su
carácter neutro.
Reacción de fisión
Es un tipo de reacción nuclear que se produce cuando un núcleo pesado se divide en dos o
más núcleos ligeros. En estas reacciones se libera mucha energía.
La fisión nuclear fue descubierta en 1939 por O. Hahn y F. Strassmann al bombardear un
núcleo de uranio-235 con un neutrón. Se produce uranio-236, un núcleo muy inestable que se
fisiona en dos núcleos más ligeros según la reacción:
235
92U

1
0n

236
92U

141
56Ba

92
36Kr
 3 01n  Energía
A pesar de que el uranio-235 es energéticamente menos estable que sus productos de fisión,
no se fisiona de forma espontánea. Es necesaria una energía de activación que se obtiene de la
captura de un neutrón por el núcleo. La energía
desprendida se puede determinar calculando
exactamente el defecto de masa entre productos
y reactivos pues aunque la suma de los números
másicos de productos y reactivos se conserva,
hay una diferencia entre el las masas
experimentales de productos y reactivos.
Una serie de consideraciones a temer en
cuenta:
1ª) El uranio-235 que permitió descubrir la
fisión nuclear no es precisamente el isótopo más
abundante del uranio. Enriquecer una muestra
de un elemento en un isótopo concreto no es
una tecnología que esté al alcance de todos los
países.
2ª) Los dos fragmentos producto de la
fisión no son siempre los mismos. En la reacción
anterior los fragmentos son el bario-141 y el kriptón-92, pero estos fragmentos son el caso más
probable de ruptura. La gráfica adjunta nos muestra cómo varía la probabilidad de fisión del
uranio-235 en función del número másico de los núcleos producto de la misma.
La mayor parte de los núcleos obtenidos en la fisión son radiactivos y dan lugar a sus
propias series radiactivas.
3ª) La energía liberada es del orden de 200 MeV por reacción, es decir, por átomo de uranio
fisionado. Si suponemos que tenemos 235 g de uranio-235, tendremos un número de Avogadro
de átomos de uranio fisionales a 200 MeV por átomo dan un total de 12 · 1025 MeV de energía = 192
· 1011 J.
- 16 -
Un kilogramo de uranio-235 produciría por fisión una energía cuya cantidad es 1.800.000
veces superior a la obtenida por quemar 1 kg de gasolina (1 kg de gasolina produciría 4’6 · 107 J).
4ª) En las reacciones de fisión se producen entre 2 y 3 neutrones, dependiendo de los
núcleos producto de la reacción de fisión. Estos neutrones pueden fisionar a otros núcleos de
uranio-235 y producir una reacción en cadena. Para que se produzca dicha reacción en cadena
debe haber un número determinado de núcleos del elemento fisionable, es su masa crítica.
Enrico Fermi fue el primer físico que produjo una reacción en cadena en 1942 en Chicago.
5ª) Otros núcleos fisionables son el torio, protoactinio, plutonio,…
Fusión nuclear
Es un tipo de reacción nuclear en la que núcleos ligeros se unen para producir un núcleo
más pesado. Sería la una reacción inversa a la fisión nuclear:
2
1
H 
3
1
H

He 
n  Energía
4
2
1
0
La energía desprendida en el ejemplo anterior es de 17’6 MeV ya que los productos
presentan un defecto de masa de 0’0189 u. El desprendimiento de energía se produce porque el
núcleo de helio-4 es más estable que los núcleos de deuterio y tritio y se desprende la energía de
enlace correspondiente.
Tal como sucede en la fisión, para iniciar un proceso de fusión nuclear es necesaria una
energía de activación. En el caso de la fusión, la energía necesaria para que los núcleos se unan
venciendo las repulsiones electrostáticas es proporcionada por una energía térmica muy elevada
(correspondiente a temperaturas superiores al millón de grados Kelvin).
Los núcleos de pequeño peso atómico, como el deuterio o el tritio, son los más adecuados
para producir fusión nuclear.
Las reacciones de fusión, también llamadas termonucleares, tienen lugar de forma natural
en el Sol y las estrellas, gracias a las altas temperaturas de su interior. De forma artificial, en
cambio, el ser humano sólo ha conseguido (hasta ahora) la fusión en cadena de forma explosiva:
se trata de la bomba de hidrógeno o bomba H. Mediante una bomba atómica de fisión se alcanza
la temperatura necesaria para llevar a cabo la reacción de fusión, es decir, en una bomba H una
bomba atómica es el detonador.
Problema
En la explosión de una bomba de hidrógeno se produce la reacción:
2
1
H 
3
1
H

He 
4
2
1
0
n
Calcule: La energía liberada en la formación de 10 g de helio.
Masa deuterio = 2’01474 u; masa tritio = 3’01700 u; masa partícula α = 4’00388 u; masa del neutrón = 1’0087 u; 1
u = 1’66 · 10-27 kg; c = 3 · 108 m/s.
Solución
- 17 -
Masa de reactivos = 2’01474 + 3’01700 = 5’03174 u
Masa de productos = 4’00388 + 1’0087 = 5’01258 u
Defecto de masa = 0’01916 u.
Pasamos ahora este defecto de masa a kilogramos con objeto de obtener la energía correspondiente en julios:
0'01916 u ·1'66 ·10-27
kg
 3'18056 ·10-29 kg
u
La energía correspondiente a este defecto de masa es:
E  mc2  3'18056 ·10-29 · (3 ·108 ) 2  2'8625 ·10-12 J
Esta energía es liberada para la formación de 4’00388 u de helio según la estequiometría de reacción nuclear del
enunciado, es decir, se ha calculado la energía liberada para la formación de un núcleo de helio-4 cuya masa es:
4'00388 u ·1'66 ·10-27
kg
 6'64644 ·10-27 kg  6'64644 ·10-24 g
u
Cuando se hayan formado por fusión 10 g de helio-4, la energía total liberada será:
2'8625 ·10-12 J
10 g ·
 4'31·1012 J
-24
6'64644 ·10 g
- 18 -
Apéndice: Espectrómetro de masas
Este instrumento se utiliza para determinar la masa de átomos y moléculas así como para
determinar la abundancia relativa de los diferentes isótopos que contiene un material. El primer
espectrómetro de masas fue diseñado por J. J. Thomson y posteriormente fue perfeccionado por F.
W. Aston, J. Dempster y K. Bainbridge.
Un esquema básico del espectrómetro es el siguiente:
Los cationes del átomo que se quiere estudiar se aceleran entre las láminas L1 y L2, entre las
que existe una diferencia de potencial de varios miles de voltios. Después los átomos pasa a través
de un selector de velocidades compuesto por un campo eléctrico y otro magnético
perpendiculares, por lo que sólo pasan los iones que se mueven a una determinada velocidad.
Luego los iones se encuentran con un campo magnético B perpendicular al plano de la figura y
describen una trayectoria circular que cumple:
Fm  Fc ;
qvB 
mv2
;
r
r
v
·m
qB
Como la razón v/qB es la misma para todos los iones, los radios son directamente
proporcionales a las masas de los iones. Los iones más pesados describen circunferencias de
mayor radio.
Como los iones de masas diferentes describen trayectorias distintas, inciden sobre la placa
fotográfica o sobre otro detector, en posiciones distintas. La masa del ión se puede calcular a
partir de su velocidad y del radio de la semicircunferencia descrita.
۞۞۞۞
Estos apuntes se finalizaron el 25 de junio de 2007 en
Villanueva del Arzobispo, Jaén (España)
Autor: Felipe Moreno Romero
- 19 -
fresenius1@gmail.com
http://es.geocities.com/apuntes_ensayos/index.htm
- 20 -