para descargar el archivo
Anuncio
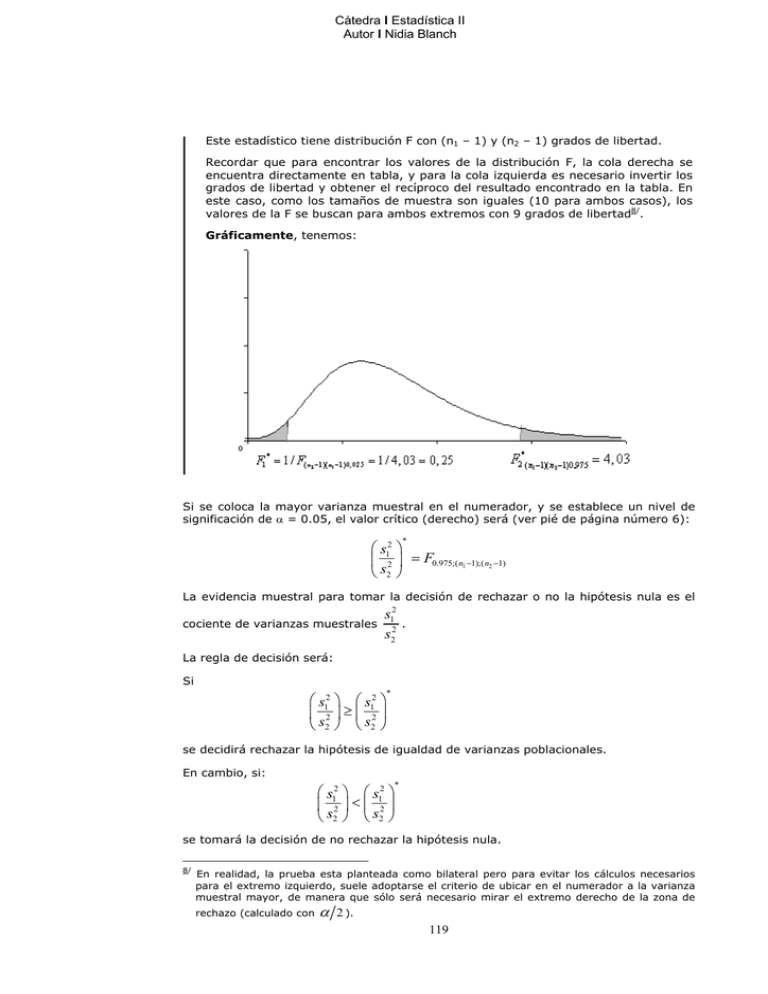
Cátedra I Estadística II Autor I Nidia Blanch Este estadístico tiene distribución F con (n1 – 1) y (n2 – 1) grados de libertad. Recordar que para encontrar los valores de la distribución F, la cola derecha se encuentra directamente en tabla, y para la cola izquierda es necesario invertir los grados de libertad y obtener el recíproco del resultado encontrado en la tabla. En este caso, como los tamaños de muestra son iguales (10 para ambos casos), los valores de la F se buscan para ambos extremos con 9 grados de libertad8/. Gráficamente, tenemos: Si se coloca la mayor varianza muestral en el numerador, y se establece un nivel de significación de α = 0.05, el valor crítico (derecho) será (ver pié de página número 6): * s12 2 = F0.975;( n1 −1);( n2 −1) s2 La evidencia muestral para tomar la decisión de rechazar o no la hipótesis nula es el cociente de varianzas muestrales s12 s22 . La regla de decisión será: Si * s12 s12 2 ≥ 2 s2 s2 se decidirá rechazar la hipótesis de igualdad de varianzas poblacionales. En cambio, si: * s12 s12 2 < 2 s2 s2 se tomará la decisión de no rechazar la hipótesis nula. 8/ En realidad, la prueba esta planteada como bilateral pero para evitar los cálculos necesarios para el extremo izquierdo, suele adoptarse el criterio de ubicar en el numerador a la varianza muestral mayor, de manera que sólo será necesario mirar el extremo derecho de la zona de rechazo (calculado con α 2 ). 119 Vamos a probar la igualdad de varianzas poblacionales en el ejemplo. s22 4.1 F= 2 = = 1.71 s1 2.4 Este cociente de varianzas muestrales se debe comparar con el valor de la distribución F graficada, que acumula el 0.975 de probabilidad y con 9 y 9 grados de libertad. F9,9,0.975 = 4, 03 El valor de F observado (1.71) es menor que el valor tabulado por lo cual se toma la decisión de no rechazar la hipótesis nula. ¿Comprende ahora por qué, al colocar siempre la mayor varianza muestral en el numerador, siempre el F observado quedará hacia el lado derecho de la distribución, y no será necesario calcular el F crítico del lado izquierdo? En consecuencia, puede considerarse que los dos grupos de familias provienen de poblaciones con varianza común σ2. Una vez comprobada la igualdad de las varianzas para los dos grupos, se calcula la varianza común s2 que es la estimación de la varianza poblacional σ2 y se pasa a probar la igualdad de las medias poblacionales. s2 = 9 x 2.4 + 9 x 4.1 9+9 = 3.25 Calculamos ahora los dos valores críticos (por tratarse de una prueba bilateral, hay un valor crítico a la izquierda y otro a al derecha): 1 1 ( x1 − x 2 ) *1 = t 0.025;18 s 2 + n1 n2 1 1 = − 2.101 3.25 + = − 2.101 x 0.81 = − 1.70 10 10 ( x 1 − x 2 ) *2 = 2 .1 0 1 x 0 .8 1 = 1 .7 0 La evidencia proporcionada por la muestra es la diferencia de medias muestrales: ( x1 − x2 ) = 25.8 − 21.9 = 3.9 Como: ( x1 − x2 ) > ( x1 − x2 )*2 se toma la decisión de rechazar la hipótesis nula. Concluimos que el consumo promedio semanal en alimentos es diferente para las zonas consideradas; de acuerdo a la evidencia, por el signo de la diferencia observada, el consumo promedio de las familias de la zona 1 es significativamente superior al consumo promedio de las familias de la zona 2. 120 Cátedra I Estadística II Autor I Nidia Blanch También es posible comparar los valores estandarizados, o sea, el valor de t observado con valores críticos obtenidos de la distribución t de Student. En este ejemplo, el valor de t observado es: t= ( x1 − x 2 ) − ( µ 1 − µ 2 ) 1 1 s2 + n1 n 2 3.9 − 0 = 1 1 + 3.25 10 10 = 3.9 = 4.81 0.81 Los valores críticos buscados en la tabla de t son t1* = - 2.101 y t2* = 2.101. La regla de decisión será: Si t < t1* o t > t2* se rechaza H0 Si t1* < t < t2* no se rechaza H0 ¿Cómo se comprueba el cumplimiento del supuesto de normalidad? El supuesto de normalidad se refiere a los residuasles (eij), pero es posible realizar pruebas de normalidad para la variable de respuesta en el estudio. Como el modelo estadístico expresa: xij = ti + eij despejando eij: eij = xij - ti Si xij se distribuye normalmente, también lo hará la variable eij pues ambas difieren solamente en una constante. Una manera de observar si la variable se distribuye normalmente consiste en graficar el histograma de los datos, o mejor utilizar un normal plot . Grafico nomal plot de la variable Valor Normal esperado consumo semanal de alimentos 30 28 26 24 22 20 18 16 18 20 22 24 26 28 30 Valor observado Los puntos están prácticamente sobre la línea recta evidenciando que podemos aceptar que la variable en estudio se distribuye aproximadamente normal. En el extremo inferior izquierdo del gráfico hay un punto que se diferencia de los demás el 121 cual corresponde a una familia que realiza un gasto en alimentos bastante menor que las demás familias encuestadas. Consumo El gráfico box plot correspondiente es: 30 28 26 24 22 20 18 16 N= 20 Consumo No se observan alejamientos importantes de la simetría de la distribución de la variable consumo en alimentos ni se observan valores atípicos. 30 28 26 24 22 20 18 15 16 N= 10 10 Zona 1 Zona 2 Zona En el gráfico anterior se han representado los consumos de alimentos para cada una de las zonas por separado. Evidentemente, los gastos en alimentos parecen ser mayores en la zona 1 en comparación con los de la zona 2. En la zona 2 aparece la familia que aparentemente consume bastante menos que las demás. De quedar bien en claro que la aplicación de la informática a la resolución de los problemas de investigación debe estar acompañada por el conocimiento de los supuestos que subyacen a la utilización de cada metodología. La responsabilidad del investigador no solamente se limita a la obtención adecuada de los datos sino también a la correcta aplicación de programas computacionales y a la cuidadosa interpretación de los resultados. La computadora solo realiza los cálculos, el investigador es el responsable de pensar. 122 Cátedra I Estadística II Autor I Nidia Blanch En síntesis, para que el problema planteado pueda ser correctamente analizado, seria necesario tomar las siguientes precauciones: 1) Establecer hipótesis adecuadas al problema. 2) Investigar la presencia de valores atípicos en los datos. 3) Tomar tamaños de muestra acordes con la variabilidad del material experimental (recordar del Capítulo I que el tamaño de la muestra depende fundamentalmente de la variabilidad). 4) Analizar el cumplimiento de los supuestos. 5) Elegir la prueba adecuada. A continuación se presenta una actividad realizada por medio de un programa de computación. En el ejemplo de los empleados de la empresa de la Pág. 100, se podría plantear como hipótesis de trabajo que los varones ganan más que las mujeres. Las hipótesis planteadas serian: H0) µ1 - µ2 = 0 H1) µ1 - µ2 ⟩ 0 siendo µ1 = salario promedio de los varones en la población µ2 = salario promedio de las mujeres en la población Estadistica descriptiva de la variable salario segun sexo de los empleados Sexo Varon Mujer Media 932,3750 Varianza 285825,125 Desv. típ. 534,62615 Media 546,1429 Varianza 29330,810 Desv. típ. 171,26240 Salario Salario Estadístico 3000 2 2000 1000 15 5 0 N= 8 7 Varon Mujer Sexo 123 Error típ. 189,01889 64,73110 La distribución del salario de los varones presenta una simetría con la presencia de un valor atípico. Las mujeres ganan todas prácticamente lo mismo y se observa la presencia de una empleada que gana bastante menos que las demás y una que gana bastante más que el resto. Prueba de muestras independientes Prueba de Levene para la igualdad de varianzas F Salario Se han asumido varianzas iguales 4,606 No se han asumido varianzas iguales Sig. ,051 Prueba T para la igualdad de medias t Diferencia Sig. (bilateral) de medias gl Error típ. de la diferencia 95% Intervalo de confianza para la diferencia Inferior Superior 1,824 13 ,091 386,2321 211,78017 -71,29109 843,75538 1,933 8,600 ,087 386,2321 199,79554 -68,96022 841,42450 En primer lugar aparece una prueba de igualdad de las varianzas poblacionales (prueba de Levene; no es la misma que hemos explicado más arriba, pero su interpretación es similar). Como el valor de significación p = 0,051 es prácticamente coincidente con α = 0,05, podemos decir que se rechaza la igualdad de las varianzas poblacionales. El nivel de significación del test de Levene se interpreta como todos los que hemos venido estudiando hasta ahora. El salario de los varones presenta mayor variabilidad que el de las mujeres9/. En general, los paquetes estadísticos presentan la salida para realizar una prueba de igualdad de medias considera las situaciones donde se acepta la igualdad de las varianza poblacionales y cuando se rechaza. En este ejemplo, la situación es la de rechazar la igualdad de las varianzas poblacionales por lo cual hay que mirar la segunda línea para interpretar la diferencia de medias y en este caso el valor “p” o valor de significación correspondiente a la diferencia de medias poblacionales es p = 0.087. Si nos atenemos a que este valor es mayor a 0.05, deberíamos concluir que no existen diferencias significativas entre los promedios de salarios de varones y mujeres en la población. Nuevamente recordamos que la hipótesis nula no se acepta, sino que “no se rechaza”, lo que indica que en este caso, no hay evidencias significativas para afirmar que el salario de los varones es mayor que el de las mujeres. Es interesante ver que, en este ejemplo, los tamaños de muestra son pequeños y en estos casos, a veces aunque exista la sospecha fundada de que la hipótesis nula es falsa, la evidencia muestral suele no ser suficiente para rechazarla. Cuando esto ocurre, si es posible, es conveniente aumentar los tamaños de muestra. Actividad 18: Los siguientes datos se refieren a cotizaciones de acciones de un banco. Indique si el agente de bolsa puede informar que no existe diferencia en los precios de dicha acción, entre la primera y la segunda quincena. Analice medias y varianzas, y utilice α = 0,01. Resumen n (quincena 1º) Media Var(n-1) E.E. Mín Máx Mediana Suma 9/ Estadística descriptiva cotización 15 n (quincena 2º) 134,40 Media 56,65 Var(n-1) 1,94 E.E. 119,17 Mín 148,73 Máx 133,71 Mediana 2016,03 Suma cotización 9 131,35 80,43 2,99 117,56 143,64 130,98 1182,11 Si bien el no cumplimiento de la igualdad de varianzas puede significar un problema como se explicó más arriba, el test de igualdad de medias se realiza pero con un estadístico modificadoVer Capítulo I, punto 9.1.2. 124 Cátedra I Estadística II Autor I Nidia Blanch Box plot 150,21 cotización 141,72 133,23 124,74 116,26 cotización-1º quinc. cotización-2º quinc. Actividad 19: El Ministerio de Educación desea estudiar el ausentismo de los docentes de nivel inicial y primario respecto a los docentes de nivel medio. Seleccionado un conjunto de docentes regulares de diversas escuelas de la provincia obtuvo la siguiente información: Descriptives NIVEL FALTAS inicial Mean 5% Trimmed Mean Median Variance Std. Deviation Minimum Maximum Range Interquartile Range Skewness Kurtosis medio Mean 5% Trimmed Mean Median Variance Std. Deviation Minimum Maximum Range Interquartile Range Skewness Kurtosis Statistic 8,9600 8,9667 9,0000 7,957 2,8208 3,00 15,00 12,00 4,0000 -,162 ,031 8,6400 8,7889 10,0000 14,573 3,8175 ,00 14,00 14,00 5,0000 -,407 -,488 Std. Error ,5642 ,464 ,902 ,7635 ,464 ,902 A continuación se presentan los correspondientes diagramas de tallo y hojas: 125 Stem-and-Leaf Plot NIVEL = inicial (1) Stem-and-Leaf Plot NIVEL = medio (2) Stem & Leaf 0 0 0 0 1 1 1 . . . . . . . Stem & Leaf 3 45 67777 88999 00000111 223 5 Each leaf: 0 0 0 0 0 1 1 1 1 case(s) . . . . . . . . 0 33 4 6666777 9 00001111 33 444 Each leaf: 1 case(s) Shapiro-Wilks (modificado)10/ nivel 1 2 Variable faltas anuales faltas anuales n 25 25 Media 8,96 8,64 D.E. 2,82 3,82 W* 0,97 0,92 p (una cola) 0,9065 0,1932 Prueba F para igualdad de varianzas Variable faltas anuales n(1) 25 n(2) 25 Var(1) 7,96 var(2) 14,5 F 0,55 p 0,1453 con un α = 0,10 ¿qué se podría decir del promedio de días de ausentismo si se comparan ambos niveles? Actividad 20: Si bien la nota promedio en el examen de Estadística fue la misma en el turno mañana y en el turno tarde, ¿se puede decir que ambos turnos presentan la misma variabilidad en las notas a un α = 0,05? Analice la salida que se presenta a continuación. ¿Es viable el supuesto de normalidad al 1%? ¿Y al 5%? Prueba F para igualdad de varianzas Variable nota n(1) 53 n(2) 50 Var(1) 4,62 Var(2) 5,51 F 0,84 p(prueba bilateral) 0,5380 Shapiro-Wilks (modificado) turno 1 2 Variable nota nota n 53 50 Media 6,38 6,40 D.E. 2,15 2,35 W* 0,93 0,92 p (una cola) 0,0158 0,0142 Actividad 21: El ingreso medio de 400 empleados de una empresa de telefonía fija es de $ 1150 con una desviación estándar de $ 110; mientras que el ingreso medio de 400 empleados de una empresa de telefonía móvil es de $ 1220 con una desviación de $ 250. ¿En base a estos datos, puede decirse que las empresas de telefonía móvil pagan mayores sueldos que las de telefonía fija? Utilice un nivel de significación del 10%. 10/ Este es otro test para probar la normalidad. Si bien no lo explicamos en este texto, su interpre tación es igual a la de todos las pruebas tal como pueden leerse en las salidas de computadora: se mira el “valor p” o “significación”, cuando es mayor con un α razonable (0,05 por ejemplo), no se rechaza la hipótesis de normalidad; si es inferior, se rechaza. En este caso no se rechaza para ninguna de las poblaciones. 126 Cátedra I Estadística II Autor I Nidia Blanch 4.4.2. Comparación de medias: muestras dependientes Esta estrategia de investigación surge cuando cada observación para un tratamiento está “apareada” con una observación para el otro tratamiento. Esta pareja esta constituida por las mismas unidades experimentales observadas en dos momentos distintos del tiempo o por dos unidades experimentales con experiencias comunes (muy similares). Es decir, se tiene dos variables aleatorias, pero no se trata de “dos muestras independientes” sino que, en general, se trata de una muestra observada en dos momentos u otra situación comparable. Se habla entonces de “muestras dependientes”. Los estadísticos anteriores no pueden utilizarse porque el error estándar (denominador del estadístico) debería ser corregido por las covarianzas, dato que en general no se dispone. La situación experimental es también diferente. Por ejemplo, se puede estudiar a un grupo de familias a las cuales se les ha preguntado acerca del gasto semanal en alimentos antes y después de haber sido beneficiadas con algún plan social de ayuda. También en esta situación podemos simbolizar a cada medición con xij, donde el subíndice i representa al tratamiento (plan social) y el subíndice j a la familia pertinente. Cada una de las mediciones representa: a) el efecto del tratamiento (ti) b) el efecto propio de la unidad experimental (la familia) que es común a ambos tratamientos (pj) c) el efecto de la variabilidad intrínseca de cada unidad experimental (eij) Expresando matemáticamente esta situación, se tiene: xij = ti + pj + eij i = 1,2 j = 1, 2, .., n La diferencia con el modelo planteado para muestras independientes es la presencia del termino pj. Este modelo presenta los mismos supuestos que en el caso de muestras independientes salvo el referido a la igualdad de varianzas poblacionales porque ahora se trabajara con una variable a la cual denominaremos diferencia y la simbolizaremos con dj. Supongamos que designamos con x1j al consumo semanal en alimentos de la familia antes de recibir la ayuda social. Luego, cada consumo estará dado por el siguiente modelo: x1j = t1 + pj + e1j x1j = consumo semanal en alimentos de la familia j antes de recibir el plan de ayuda social t1 = efecto del tratamiento (ayuda social) pj = efecto común asociado a la j-esima familia e1j = error experimental no controlado por el investigador social El consumo en alimento de una familia después de recibir la ayuda social será: x2j = t2 + pj + e2j Introducimos ahora una variable diferencia que simbolizaremos con dj11/. dj será la diferencia entre el consumo de la j-ésima familia antes y después de recibir la ayuda social. 11/ Revisar en el Capítulo I, el tema 9.2. 127 En símbolos: dj = x1j – x2j = (t1 + pj + e1j) – (t2 + pj + e2j) = (t1 – t2) + (e1j – e2j) Al efectuar, la diferencia, ha desaparecido el termino pj. Esto implica que se ha eliminado el efecto común asociado a la familia j. Entonces, cuando se trabaja con muestras dependientes conviene utilizar como variable la diferencia de las respuestas de las familias antes y después de la aplicación del plan de ayuda. La diferencia refleja el efecto del plan antes y después y no se ve influenciada por la situación de la familia antes o después en relación a la media de su propio grupo. El termino t1 – t2 es constante para todas las unidades experimentales y el termino e1j – e2j varia de unidad experimental a otra (es la variable aleatoria que consideramos). Podemos calcular el promedio de la variable di como: n d= ∑ dj j =1 n = ∑ (t1 − t2 ) j =1 n + ∑ (e1 j − e2 j ) j =1 n n n (t − t ) = n 1 ´2 + (e1 − e2 ) = (t1 − t2 ) + (e1 − e2 ) n Un ejemplo: Supongamos que una empresa esta implementando un programa para disminuir la cantidad de horas hombre perdidas mensualmente por accidentes de trabajo. Las mediciones se hicieron 6 meses antes y 6 meses después de ponerse en marcha un plan de seguridad industrial. Este es un caso típico de experimento antes-después pues el mismo periodo (un mes) en la misma empresa, es medido antes y después de ponerse en marcha el plan de seguridad industrial. Tener en cuenta que si el plan tuvo éxito, la media “antes” se espera sea mayor que la media “después”, esto se refleja en la hipótesis alternativa, con una diferencia “antes” menos “después” positiva); si se rechaza la hipótesis nula, será que el plan tuvo éxito; si no se puede rechazarla, con esos seis meses no se puede probar su efectividad. La hipótesis nula será: H 0 : µantes ≤ µdespues µantes − µ despues ≤ 0 o o, como se planteó en el Capítulo I llamando cionales en este caso: ∆ a la diferencia de medias pobla- H 0 )∆ ≤ 0 y la alternativa: H1 ) µantes > µdespues o o µantes − µdespues > 0 H1 ) ∆ > 0 128 Cátedra I Estadística II Autor I Nidia Blanch Calculamos ahora el promedio de la variable diferencia, estadístico que se utilizara como criterio de test o medida de discrepancia para tomar una decisión en cuanto a la hipótesis nula. d = x1 − x2 La esperanza será: E (d ) = E ( x1 − x2 ) = µ1 − µ 2 por lo cual se puede concluir que medias poblacionales12/. d es un buen estimador de la diferencia de Luego, si d se distribuye aproximadamente normal, el estadístico: d − ( µ1 − µ2 ) sd2 n ~ tn −1 se distribuye como una t de Student con n – 1 grados de libertad. Para finalizar el procedimiento de test de hipótesis nos falta especificar los valores críticos y las reglas de decisión. Si la hipótesis es bilateral se deben calcular dos valores críticos utilizando a la distribución t. En este caso es unilateral, por lo tanto se calcula sólo el valor crítico derecho. 12/ A fin de comprender mejor la ventaja de trabajar con este tipo de muestras cuando las variables están correlacionadas, veremos qué ocurre con la varianza de dj, en término de las varianzas de las x: sd2 j = s 2 ( x1 j−x2 j ) = sx21 j + sx22 j − 2 cov( x1 j , x2 j ) = sx21 j + sx22 j − 2r12 s1s2 siendo r12 el coeficiente de correlación lineal que existe entre las mediciones. Esta varianza no necesita ser calculada de esta forma ya que el estadístico la calcula directamente a partir de las diferencias. Una de las ventajas primordiales de los diseños de mediciones repetidas es la reducción potencial de la varianza debida al error experimental. Para este diseño: sd2 = s(2x1 − x2 ) = sd2 s12 s22 ss = + − 2r12 1 2 n n n n Mientras la correspondiente estimación para el caso de observaciones no correlacionadas (muestras independientes) sería: s(2x1 − x2 ) = s12 s22 + n n Si la correlación entre las observaciones es positiva, la estimación del error experimental de un diseño de comparaciones dependientes donde se emplea sd2 diseño de observaciones no correlacionadas en el factor 2r12 s1s2 . Si en cambio ocurriera que será menor que la obtenida de un esa correlación es nula (situación posible aunque infrecuente), entonces convendría hacer la prueba como si se tratara de dos muestras independientes. Las salidas de programas de computación, incluyen siempre para estos casos una prueba de hipótesis que permite inferir si la correlación existe o no. 129 Gráficamente, tenemos: los valores críticos (si fuera bilateral) se calculan como: d1* = −tn −1;α / 2 sd2 n y d 2* = tn −1;1−α / 2 sd2 n la regla de decisión será: Si d < d1* o d > d 2* Si d1* < d < d 2* se rechaza H0 no se rechaza H0 Como en este ejemplo la prueba es unilateral, sólo se calcula el punto crítico del lado derecho, con el valor tabulado correspondiente a α . Siguiendo con el ejemplo de la seguridad industrial para evaluar si disminuyeron las horas hombre perdidas por mensualmente por accidentes de trabajo. Para probar la hipótesis planteada más arriba, se deben calcular la media y la varianza de la variable diferencia en la muestra: d y sd2 . Los resultados evaluados durante 6 meses fueron: Meses 1 2 3 4 5 6 Antes del programa 38 64 42 70 58 30 Después del programa 31 58 43 65 52 29 n ∑ dj 24 d = i =1 = = 4 6 n 130 dj 7 6 -1 5 6 1 24 dj2 49 36 1 25 36 1 148 Cátedra I Estadística II Autor I Nidia Blanch n sd2 = 2 2 ∑ d j − nd j =1 = n −1 sd2 = 148 − 96 5 = 10.4 sd2 10.4 = = 1.73 n 6 sd = 1.73 = 1.31 A continuación buscamos el valor de t con n – 1 = 6 – 1 = 5 grados de libertad. Si se fija α = 0.05, se tiene t5;0.95 = 2,02 El valor crítico será: d * = 2.02 x1, 31 = 2, 65 Regla de decisión: Si d > 2, 65 se rechaza Si d < 2, 65 H0 no se rechaza H0 Como d = 4 , estamos en la primera situación por lo cual concluimos que el plan de seguridad industrial ha sido exitoso. El promedio mensual de horas hombre perdidas por accidentes de trabajo se han reducido después de la implementación del plan (la media “antes” es mayor que la media “después”). A continuación repetimos este ejemplo, pero resuelto mediante la salida de un programa de computación. Aquí, tal como comentábamos más arriba, primero se calcula el coeficiente de correlación y se prueba su significación: si ésta no fuera significativa convendría utilizar el test para muestras independientes. Si bien el tratamiento del test acerca del coeficiente de correlación se hace en otro capítulo, digamos que si en la salida de computación se observa el “valor de significación” (p) y si es menor que el α entonces se concluye la conveniencia de usar esta prueba de muestras apareadas. Esto es lo que ocurre en este ejemplo, donde Sig = 0,001 (o también llamado “p”). Correlaciones de muestras relacionadas Coeficiente de correlacion lineal n Par 1 ANTES y DESPUES 6 Sig. ,981 ,001 Prueba de muestras relacionadas Diferencias relacionadas Media Par 1 ANTES - DESPUES 4,0000 Error típ. Desviación típ. de la media 3,22490 1,31656 131 95% Intervalo de confianza para la diferencia Inferior ,6157 Superior 7,3843 t 3,038 gl Sig. (bilateral) 5 ,029 Las salidas de computación para este tipo de problemas, generalmente proporcionan el “valor de significación” para las dos colas (bilateral); en este caso es 0,029. Pero como la prueba es unilateral, en la cola derecha queda sólo la mitad de este valor (0,029/2 = 0,015) que es inferior a 0,05 y por lo tanto se toma la decisión de rechazar la hipótesis nula, el mismo resultado obtenido trabajando a mano. (Es interesante observar en este caso, que si α hubiera sido 0 ,01, la hipótesis no se hubiera rechazado. ¿Qué les sugiere esa aparente contradicción?). Actividad 22: En un laboratorio se está probando la acción de una sustancia "H" sobre determinado tipo de tumor. Para ello se seleccionaron 80 conejos de iguales características (especie, procedencia, etc.) a los que se había injertado el tumor y se los dividió en dos grupos, al primero se lo trató con dicha sustancia mientras que al segundo no, y se computó los días de sobrevida de cada uno. El informe presentado por el laboratorio contenía dos salidas de un soft estadístico. Explique de qué se trata la información presentada, la herramienta estadística utilizada en cada caso y seleccione la que resulta adecuada en este caso concluyendo respecto de la efectividad de la sustancia “H” en el tratamiento del tipo de tumor que se está estudiando. Prueba T (muestras apareadas) Obs(1) Obs(2) N media(dif) DE(dif) Trat. No trat. 40 2,80 2,33 LI(99%) 1,80 LS(99%) T p(2 colas) 3,80 7,59 <0,0001 Prueba T (muestras independientes) Variable Ds.de sobrev Grupo(1) Trat. LI(99%) 1,72 LS(99%) 3,88 Grupo(2) No Trat. n(1) 40 n(2) 40 p(Var.Hom.) 0,3755 media(1) 28,85 T 6,87 media(2) 26,05 p <0,0001 Normal Q-Q Plot of DIFERENC 8 6 Expected Normal Value 4 2 0 -2 -2 0 2 4 6 8 10 Observed Value Actividad 23: La Escuela de Graduados de la Facultad está invitando a los profesionales a participar de su oferta académica (Maestrías y Posgrados) aduciendo que el ingreso individual aumenta luego de realizar algún curso superior. Esta afirmación se basa en un estudio realizado sobre 15 participantes de sus cursos a los que se les preguntó sus ingresos mensuales antes y después de egresar. Con los datos obtenidos. 132 Cátedra I Estadística II Autor I Nidia Blanch a) ¿Está en lo cierto la Escuela de Graduados? Trabaje con α = 0,10 b) En caso afirmativo, ¿cuántos pesos más ganan los profesionales luego de graduarse, en promedio? Graduado 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 $ antes 900 1260 1750 1100 800 2100 1700 1380 1000 1550 3500 2600 1250 1450 2100 $ después 1300 1500 1750 1100 1100 2100 2000 1500 1600 1800 3500 2600 1500 1450 2500 4.4.3. Comparación de dos proporciones, muestras independientes Seguimos en la situación de investigación en que se seleccionan dos muestras de dos poblaciones pero ahora la variable en consideración es dicotómica (éxito o fracaso), el interés se centra en la comparación de la proporción de éxitos entre ambas poblaciones. Supongamos que se ha efectuado una encuesta a 1469 jefes de hogar de una cierta comunidad, una de las preguntas estaba referida al sexo y otra a si eran beneficiarios o no de un plan jefes y jefas de hogar. Los resultados se encuentran volcados en la siguiente tabla: Sexo Beneficiarios plan No beneficiarios plan Total Varones 117 950 1067 Mujeres 54 348 402 Total 171 1298 1469 La hipótesis de trabajo es que la asignación de planes a los jefes no es igual para hogares con jefes varones o mujeres. Las hipótesis planteadas son: H0) P1 = P2 o P1 - P2 = 0 H1) P1 ≠ P2 o P1 - P2 ≠ 0 P1 = proporción de jefes de hogar mujeres beneficiarias del plan P2 = proporción de jefes de hogar varones beneficiarios del plan El parámetro establecido en las hipótesis es una diferencia de proporciones poblacionales y, por lo tanto, lo lógico seria pensar que su mejor estimador puntual será la diferencia de proporciones muestrales: ¿Cuál es la distribución de este estimador? 133 pˆ1 − pˆ 2 . (Sugerimos revisar la cuestión en el Capítulo I , punto 9.3.). Ya se ha visto que si los tamaños muestrales son suficientemente grandes (nP y nQ > 5 para ambas poblaciones en este caso), se tiene: PQ P Q pˆ1 − pˆ 2 ~ N ( P1 − P2 ); 1 1 + 2 2 n1 n2 En el Capítulo I, al desconocer los valores de P1 y P2 se utilizaron en el estadístico sus estimadores. Pero ahora, aunque éstos siguen siendo valores desconocidos, la hipótesis nula establece su igualdad13/. El estadístico que sería: ( p1 − p2 ) − ( P1 − P2 ) ~ N (0,1) PQ P2Q2 1 1 + n1 n2 Se modifica ya que al suponer que P1 – P2 = 0, la estimación de esa proporción “común’ a ambas poblaciones puede hacerse combinando ambas muestras (éste estimador se conoce como p amalgamado): p= n1 pˆ1 + n2 pˆ 2 n1 + n2 Los puntos críticos serán los correspondientes a la distribución normal estandarizada, y la regla de decisión: Si z < -z* o si z > z* se rechaza H0 Si –z* < z < z* no se rechaza H0 Calcularemos ahora el estadístico con los datos del ejemplo: pˆ 1 = pˆ 2 = p= 54 = 0.1343 402 117 402x0.13 +1067x0.11 402 +1067 z= (0.13 - 0.11) 0.115x0.885 402 + = 0.115x0.885 = 169.63 = 0.115 1469 0.02 0.00025 + 0.00009 = 0.02 = 1.05 0.019 1067 Si fijamos α = 0.05, los valores de 13/ = 0.1097 1067 z * son ± 1.96. Recordar que siempre en las pruebas de hipótesis el estadístico se construye “suponiendo que la hipótesis nula es verdadera”. 134 Cátedra I Estadística II Autor I Nidia Blanch 135




