MOVIMIENTO EN EL EJE Y (CAIDA LIBRE) Una aplicación

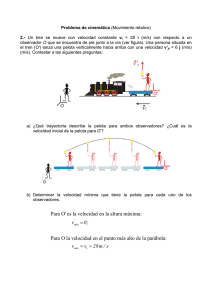
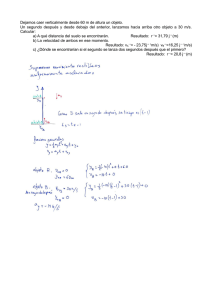
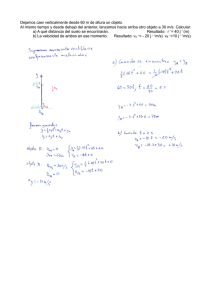
1
MOVIMIENTO EN EL EJE Y (CAIDA LIBRE)
Una aplicación importante del movimiento rectilíneo uniformemente acelerado es la caída libre.
Todos los cuerpos caen (o suben) con una aceleración constante denominada aceleración de la
gravedad que es aproximadamente igual a 9.81 m/s2 y está dirigida hacia el centro de la Tierra. El
conjunto de ecuaciones del movimiento rectilíneo uniformemente acelerado es suficiente para los
problemas de caída libre:
v = at + v0
v 2 = v 0 + 2ax
x = 12 at 2 + v0t
2
Así que:
Las ecuaciones que utilizamos son las misma que las del MURA, con la diferencia que empleamos el
valor de g en vez de a , por lo tanto se tiene:
g = 9,8
m
s2
v = v0 ± g · t
x = v0. t ±
1
2
. g. t2
v2 = v 0 2 ± 2. g. x
Se usa el signo “+” cuando el lanzamiento vertical es hacia abajo y se usa el signo “-” cuando el
lanzamiento vertical es hacia arriba.
http://www.educaplus.org/movi/4_2caidalibre.html
http://www.educaplus.org/movi/4_3tparabolico.html
1. Una pelota se lanza verticalmente hacia arriba. En el punto más alto ¿cuánto vale su aceleración?¿y su
velocidad?
2. Una pelota se lanza hacia arriba. Mientras está en el aire, su aceleración es?:
3. Un objeto proyectado hacia arriba con velocidad inicial v0 alcanza una altura h. ¿Qué altura alcanzará
otro objeto proyectado hacia arriba con velocidad inicial 2v 0 ?
4. Un rifle dispara una bala verticalmente hacia arriba con una velocidad en la boca del arma de 300 m/s.
Despreciando el rozamiento con el aire, ¿cuál es la altura máxima alcanzada por la bala?
5. Se lanza una pelota hacia arriba con una velocidad inicial de 20 m/s.
Por
Ingeniera Margarita Patiño Jaramillo
Ingeniera Gloria María Díaz Londoño
Para el I.T.M
2
a) ¿Cuánto tiempo está la pelota en el aire?
b) ¿Cuál es la mayor altura alcanzada por la pelota?
c) ¿Cuándo está la pelota a 15 m por encima del suelo?
6. Tito lanza una piedra hacia arriba desde la terraza de un edificio de 50 m
de alto, con una rapidez inicial de 20 m/s. Cuando está cayendo la piedra
pasa justo por el costado del edificio. Calcular
a) El tiempo para que la piedra alcance su altura máxima,
b) La altura máxima,
c) El tiempo que tarda en pasar por el punto inicial,
d) La velocidad de la piedra en ese instante,
e) El tiempo que tarda en llegar al suelo,
f) La velocidad en ese instante.
7. Un globo inflado con aire caliente se eleva verticalmente con una rapidez constante de 5 m/s. Cuando
está a 50 m sobre el suelo, se deja caer un paquete desde el globo.
a) Calcular el tiempo que tarda el globo en llegar a los 50 m.
b) ¿Cuánto tiempo demora el paquete en llegar al suelo después que se ha soltado?
c) ¿Cuál es la velocidad del paquete justo antes de llegar al suelo?
d) Repetir b) y c) para el caso en que el globo desciende a 5m/s desde una altura de 50 m.
R: a) 10s, b) 3.7s, c) –32 m/s.
8. Se lanza un cuerpo hacia arriba, en dirección vertical, con velocidad inicial de
98 m/s desde el techo de un edificio de 100 m de altura. Tomar g = 9.8 m/s2.
Hallar:
a. La máxima altura que alcanza el cuerpo medida desde el suelo
b. El tiempo que transcurre hasta que llega al suelo.
c. La velocidad al llegar al suelo
Por
Ingeniera Margarita Patiño Jaramillo
Ingeniera Gloria María Díaz Londoño
Para el I.T.M
3
9. Se lanza una pelota verticalmente hacia arriba con una velocidad de 20 m/s desde la azotea de un
edificio de 50 m de altura. La pelota además es empujada por el viento, produciendo un movimiento
horizontal con una aceleración de 2 m/s2. Calcular:
a. La distancia horizontal entre el punto de lanzamiento y de
impacto
b. La altura máxima
c. Los instantes y los valores de las componentes de la velocidad
cuando la pelota se encuentra a 60 m de altura sobre el suelo.
d. Los valores de las componentes tangencial y normal de la
aceleración en dichos instantes.
10. Se deja caer una piedra dentro de un pozo que contiene agua, si el sonido del choque de la piedra con
el agua tarda en escucharse 2 segundos, encuentre la profundidad del pozo hasta el nivel del agua.
La velocidad del sonido es de 340 m/s
11. Una pelota se deja caer desde cierta altura, y cuando le faltan 10 metros para
llegar al suelo, su velocidad es de 30 m/s ¿Desde qué altura se dejó caer?
12. Se deja caer una piedra desde un elevado precipicio y i segundo más
tarde es lanzada otra piedra verticalmente hacia abajo, con una velocidad de
18 m/s. Calcular a qué distancia por debajo del punto más alto del
precipicio, alcanzará la segunda piedra a la primera.
Por
Ingeniera Margarita Patiño Jaramillo
Ingeniera Gloria María Díaz Londoño
Para el I.T.M
4
13. Un malabarista actúa en una habitación cuyo techo se encuentra a 2,7 metros por encima de sus
manos. Lanza verticalmente hacia arriba una pelota de modo que alcance justamente el techo.
a. ¿Con qué velocidad inicial deberá lanzar la pelota?
b. ¿Cuánto tiempo tardará la pelota en alcanzar el techo?
c. En el instante en que la pelota alcanza el techo, lanza hacia arriba otra pelota con la misma velocidad
inicial, al cabo de cuánto tiempo después de lanzar la segunda, se cruzan ambas pelotas?
d. ¿A qué distancia, por encima de las manos del malabarista, se cruzan las dos pelotas?
14. Desde un objeto que es sacado de un pozo con la
velocidad constante de 2 m/s, se deja caer una piedra esta
llega al fondo en un tiempo de 1.2 segundos. Determina:
a) la altura desde la cual se dejó caer la piedra.
b) la velocidad con la cual llegó al fondo.
15. Una botella se deja caer desde el reposo en la posición X =
20 m e y = 30 m. Al mismo tiempo se lanza desde el origen
una piedra con una velocidad de 15 m/s.
a. Determinar el ángulo con el que tenemos que lanzar la
piedra para que rompa la botella, calcular la altura a la que ha
ocurrido el choque.
b. Dibujar en la misma gráfica la trayectoria de la piedra y la
botella.
Por
Ingeniera Margarita Patiño Jaramillo
Ingeniera Gloria María Díaz Londoño
Para el I.T.M
5
16. a. A que velocidad debe ser lanzada una bola verticalmente desde el nivel del piso para elevarse a una
altura máxima de 50m?
b. ¿Cuánto tiempo estará en el aire?
17. Una roca es lanzada desde un risco de 100m de alto ¿cuánto tiempo tarda en caer a los:
a) primeros 50m y
b) los segundos 50m?
105. Un armadillo salta hacia arriba (fig.) alcanzando 0.544m en 0.2005.
a) ¿Cuál es su velocidad inicial?
b) ¿Cuál es su velocidad a esta altura?
c) ¿Qué altura puede alcanzar?
18. Una bola de arcilla cae en el piso de una altura de1.50m. Esta en contacto con el piso por 20.m/s
antes de llegar al reposo.
¿Cuál es la aceleración promedio de la bola durante el tiempo que esta en contacto con el piso (considere
la bola como una partícula)?
19. Para probar la calidad de una pelota de Tenis, la tiras hacia el piso a una altura de 4.00m. Está rebota
a una altura de 3.00 m.
Si la bola estuvo en contacto con el piso por 10.0 ms, ¿cuál es la aceleración promedio durante el
contacto?
20. Dos objetos empiezan una caída libre desde el reposo desde la misma altura a un 1.0s de diferencia.
¿Cuánto tiempo después de que el primero empieza a caer, los dos objetos estarán 10 m aparte?
21. Un globo de aire caliente esta ascendiendo a una velocidad de 12m/s -y está 80m arriba del suelo,
cuando un paquete es tirado por un lado.
a) ¿Cuánto tiempo le tomará al paquete llegar al suelo?
b) ¿Con qué velocidad golpea el piso?
110. Si una pulga salta una altura de 0.640m.
a) ¿Cuál es su rapidez inicial en el instante que abandona el terreno?
b)¿Qué tiempo permanece en el aire?
22. Una piedra es lanzada hacia arriba verticalmente con una rapidez de 8m/s de la azotea de un edificio
de 12m de altura. Para el movimiento de la roca entre la azotea de edificio y el terreno,
Por
Ingeniera Margarita Patiño Jaramillo
Ingeniera Gloria María Díaz Londoño
Para el I.T.M
6
a) ¿cuál es la magnitud y dirección.
b) La velocidad promedio de la roca?
c) La aceleración de la roca?
23. Un huevo es lanzado verticalmente hacia arriba de la cornisa de un edificio muy alto. Cuando el huevo
regresa al nivel de la cornisa, 7s más tarde, éste a recorrido 50m hacia debajo de la cornisa.
a) ¿Cuál es la rapidez inicial del huevo?
b) ¿Cuál es la altura que alcanza el huevo a partir de su punto de lanzamiento?
c) ¿Cuál es la magnitud de su velocidad en el punto más alto?
d) ¿Cuál es la magnitud y dirección de su aceleración en el punto más alto?
24. Una partícula A se mueve a lo largo de la línea y = d(30m) con una velocidad constante v(v = 3.0 m/s)
dirigida paralelamente al eje x positivo. Una segunda partícula B comienza en el origen con una velocidad
cero y aceleración constante a (a = 0.40 m/s2) en el mismo instante en que la partícula A ara el entre a y el
eje y positivo resultaría en una colisión θeje y. ¿Qué ángulo entre dos partículas?
25. Una regadera gotea en el baño hacia el piso a 200 cm. abajo. Las gotas caen en un intervalo regular de
tiempo. La primera gota golpea en el piso en el instante en que la cuarta gota empieza a caer. Encuentre
las localizaciones de la segunda y tercera gota cuando la primera golpea el piso.
Por
Ingeniera Margarita Patiño Jaramillo
Ingeniera Gloria María Díaz Londoño
Para el I.T.M