Simulación de fresado mediante corte interrumpido en torno para

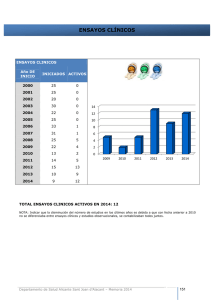
Asociación Española de
Ingeniería Mecánica
XVIII CONGRESO NACIONAL
DE INGENIERÍA MECÁNICA
Simulación de fresado mediante corte interrumpido en torno para
medición de temperaturas en la herramienta de corte
I. Ansoategui, A. Martínez, O. Pereira, J. Aguirrebeitia, A. Lamikiz, U. Garitaonaindia
Dpto. Ingeniería Mecánica. Univ. del País Vasco UPV/EHU
igor.ansoategui@ehu.es
Resumen
En este trabajo se aborda la simulación del fresado mediante un corte interrumpido en torno. El objetivo
principal de este trabajo es conocer las temperaturas que se alcanzarán en la cara de desprendimiento de la
herramienta en el proceso de corte.
Para conseguir este objetivo se va a hacer una extrapolación del proceso de torneado al proceso de fresado, lo
cual es posible si se tornea una pieza ranurada longitudinalmente, simulando así el torneado como si de un
fresado se tratara, al ser el fresado un corte interrumpido.
Para poder realizar estas medidas de temperatura en las condiciones de ensayos se hará uso de un termopar
tipo K que se colocará a una distancia de 0,5 mm de la cara de desprendimiento de la plaquita. La temperatura
media en el contacto se estimará a partir de un modelo teórico de conducción de calor.
Se han realizado diferentes ensayos para diferentes condiciones de corte que serán descritas en profundidad.
Además de esto se estudiará también la diferencia de temperatura que se alcanzará para corte continuo e
interrumpido usando por una parte mismo tiempo de corte, y por otra, misma longitud efectiva de corte.
CONDICIONES INICIALES
Para conseguir los objetivos marcados en la citada simulación se han realizado una serie de ensayos, los cuales
se han llevado a cabo en el centro de torneado modelo LEALDE TCN 10.
Estos ensayos se han realizado con dos materiales diferentes, por una parte tenemos un acero AISI 4340 (F1272,
40NiCrMo7) dureza 35 HRc, el cual es un material de alta dureza y difícil maquinabilidad, y por lo tanto será de
interés saber las temperaturas obtenidas en este material. El otro material que se ha usado, un aluminio AW 2030
HB108. La razón de tomar este material para realizar los ensayos es comparar las temperaturas obtenidas en
ambos casos. Lo normal es que en aluminio, al tratarse de un material de baja dureza, las temperaturas que se
alcancen sean bastante menores a las que obtendremos en los ensayos del acero citado.
Las probetas que se han utilizado han sido piezas cilíndricas de 60 mm de diámetro, 300 mm de longitud, y 240
mm de longitud de corte útil. Además de máquinas, herramientas y piezas, se ha requerido para los ensayos de
un termopar tipo K para la medida de temperaturas, taladrina para los ensayos con refrigerante, ordenador dotado
de una tarjeta de adquisición de datos, programa de conversión de voltios a grados instalado en el citado
ordenador (Labview 6.0), bus de direcciones, y un amplificador de señal (0-10V, 0-1200º C).
METODOLOGÍA
En este artículo abarcaremos dos estudios más o menos diferenciados, con sus correspondientes variables, pero
todos ellos relacionados de forma directa.
Variación De La Temperatura De Estabilización Con El Ángulo Evolvente θmáx
El primer estudio que realizaremos será la estabilización de la temperatura en el proceso de fresado tangencial
para diferentes valores de la θmáx , ángulo evolvente (ver Fig. 1). Para los ensayos con acero y aluminio,
I.Ansoategui et al. / XVIII Congreso Nacional de Ingeniería Mecánica (2010)
2
representaremos en la mismas gráficas las temperaturas de estabilización, usando una gráfica diferente para cada
valor de θmáx. Si los datos salen concordantes deberíamos de obtener una temperatura de estabilización para el
corte interrumpido en aluminio bastante menor que en el acero. Haremos un total de 11 pasadas a lo largo de las
cuales iremos variando el valor de θmáx. Cada una de estos ensayos tendremos que repetirlos en seco, con MQL y
con taladrina.
Comparación Entre la Temperatura de Estabilización en Continuo e Interrumpido
Esta comparación la vamos a hacer tomando dos suposiciones, la primera con igual tiempo de corte y la segunda
con igual longitud de corte efectiva.
Cuando nos referimos a igual tiempo de corte hablamos de que la longitud de pieza que estamos cortando sea la
misma, o lo que es lo mismo, que el tiempo que dura la operación de torneado sea el mismo. Lógicamente, si
estamos cilindrando la misma longitud de pieza la cantidad de material que estamos cortando será mucho menor
en el corte interrumpido que en el corte continuo de la misma longitud de pieza, por tanto las temperaturas de
estabilización que se alcancen en el primer caso deberán de ser sensiblemente inferiores a las que se obtengan en
el segundo.
Cuando nos referimos a igual longitud efectiva de corte estamos hablando de la longitud durante la cual está
cortando, por tanto en la pieza ranurada estaremos cortando aproximadamente la 5ª parte de lo que estamos
cortando para la pieza continua en la misma longitud, por tanto para conseguir realizar esta hipótesis tomaremos
aproximadamente la quinta parte de la longitud del tocho. Observaremos la estabilización en continuo frente a
interrumpido.
Estos ensayos los realizaremos para aluminio y acero, representándolos en gráficas diferentes. Estos ensayos
serán repetidos en seco, MQL y taladrina.
EQUIVALENCIAS Y CÁLCULOS
El estudio que queremos llevar a cabo es la simulación del fresado mediante un torneado interrumpido pero este
estudio necesita de una sería de cálculos matemáticos para que esta analogía sea posible.
A continuación, vemos una figura en la que se resumen las condiciones que necesitamos que se cumplan para
poder hacer la simulación del fresado mediante el torneado interrumpido.
Fig. 1. Parámetros fundamentales en el Fresado (1) y Torneado (2).
Volv1 = Volv2
lc1 = lc2
f z = ft
a r  0,6365  aa
(1)
Simulación de fresado mediante corte interrumpido en torno para medición de temperaturas en la herram.
1   2
 max lc

 D L
3
1   2
(2)
La fresa que tomaremos para los cálculos será una fresa diámetro 12 mm y de dos dientes. Para la realización de
los ensayos para ambos materiales en el torno usaremos una velocidad de giro de nt= 800 r.p.m., y un avance f=
0,2 mm/rev.
Teniendo en cuenta los datos iniciales considerados anteriormente pasaremos a calcular los parámetros de
equivalencia.
Velocidad de Rotación Equivalente en Fresado
Por una parte tenemos por la expresión de la velocidad periférica:
vt = vf →
wt · rt = wf · rf
Siendo:
vt = velocidad periférica en el torneado (m/s), vf = velocidad periférica en el fresado (m/s), wt = velocidad de
rotación en el torneado (rad/s), wf = velocidad de rotación en el fresado (rad/s), rt = radio de la pieza en el
torneado (m) y, rf = radio de la fresa (m).
Sin más que sustituir en la expresión anterior los datos dados obtenemos:
800 
2 
 0,03  w f  0,06
60
w f  418,879 
60
 4000 r. p.m
2 
(3)
Tenemos que tener en cuenta que según vamos comiendo material el radio de la pieza rt va disminuyendo su
valor, por tanto, al mantenerse constante la velocidad de rotación para los ensayos realizados la consecuencia es
que la velocidad de rotación de la fresa irá disminuyendo, llegando esta disminución hasta un valor de unas 3000
r.p.m.
Avance Equivalente en Fresado
Hemos dicho que hemos considerado un avance en torneado de 0,2 mm/rev. Tenemos que tener en cuenta que el
avance debe ser igual en ambos casos, y también cual es el trozo en el que estamos comiendo. Sabiendo que la
pieza tiene hechas 5 ranuras, y que éstas dividirán a la pieza de fresado en 10 franjas (corte y no corte), pero que
no sabemos qué ángulo abarca cada franja, ya que esta es variable con el radio de la pieza, podremos decir que:
0,2 mm / rev
 fz
2  /
f franja  f z
(4)
Siendo:
ffranjta_t = avance por franja de la pieza de torno, fz = avance por diente en el fresado y, θ = ángulo que abarca una
franja.
Equivalencia de los Procesos de Corte
Para poder hacer la equivalencia entre ambos procesos de corte tenemos que tener en cuenta dos cosas. Por una
parte, la longitud de corte, donde tenemos que conseguir que esta sea análoga en ambos casos para que el tiempo
de corte sea el mismo. Por otro lado, el volumen de viruta, donde tenemos que conseguir que este sea análogo
para que la cantidad de material comida sea la misma en ambos casos.
Por lo tanto, teniendo en cuenta las consideraciones anteriores, tendremos dos ecuaciones que nos dejarán como
única variable la profundidad de corte ap.
lc 
Donde:
df
2
  max  a p
Vf
df
V
ap
1
(5)
I.Ansoategui et al. / XVIII Congreso Nacional de Ingeniería Mecánica (2010)
4
fz = avance por diente, df = diámetro de fresa, ap = profundidad de corte, Vf = velocidad de avance y, V =
velocidad de corte.
Fórmula que responde a la geometría del fresado:
Fig. 2. Geometría de corte en el fresado.
Por una parte que el volumen arrancado en fresado en cada virutazo puede simplificarse de la forma:
Vol f  f z  d f  a p
(6)
Y si además tenemos en cuenta que el volumen de viruta arrancado en torneado es:
Q
1000  V  a p  f
(7)
60
Y sabiendo que tenemos que igualar el volumen arrancado en cada virutazo de fresado al material arrancado en
cada franja de torneado, tendremos la igualdad siguiente:
1000  V  a p  f z  mm 3  1  min 
 seg 
   
 
  60  

60
 min 
 seg  nt  rev 
f z  d f  l  mm 3 
2 


(8)

Vamos a tomar un valor de la profundidad de pasada en fresado de 1mm. Para resolver la ecuación anterior
necesitamos la velocidad periférica, por tanto en primer lugar calculamos esta:
V
  d t  nt
1000

  60  800
1000
 150,796
m
min
(9)
Tenemos que tener en cuenta que esta velocidad de corte es sólo para un diámetro de 60 mm de tocho, por tanto
para un diámetro de pieza diferente tendrá un valor distinto.
Si sustituimos este valor en la ecuación anterior:
1000 150,796  a p 
0,2 
12  l  mm 3 
2 


60
0,2 
3
2     mm   1   min   60   seg 
 seg  800 rev
 min 




2 

Como podemos observar en principio nos falta un dato más para poder operar, el valor de θ. Este valor lo
obtenemos sustituyendo valores en la fórmula para la longitud de corte en fresado, e igualándola a la que habrá
en torneado, es decir
lc 
df
2
  max  a p
Vf
df
V
ap
 1  rt  
(10)
Simulación de fresado mediante corte interrumpido en torno para medición de temperaturas en la herram.
5
Sustituyendo valores obtendremos:

 2  4000
12
0,012
60
   0,001 2  

 1  
2
150,796
0,001
2
→
  0,628 rad  36º
(11)
Que era el resultado que esperábamos obtener, ya que estamos haciendo ranuras igualmente espaciadas, y por lo
tanto al haber un total de 10 franjas longitudinales, cada franja ocupará 360/10= 36º. Las franjas en el tocho
metálico anteriormente mencionado las haremos por medio de una fresa de un diámetro determinado. Si
calculamos la longitud periférica de cada franja:
l franja  r1  
0,06
 0,6277  18,831 mm
2
(12)
Por lo tanto, si tenemos en cuenta que esta longitud está medida sobre la periferia de la pieza, deberemos coger
una fresa de diámetro algo menor a este valor. Si miramos los diámetros de fresas más apropiados para este caso,
vemos que una fresa de diámetro 18 mm es la adecuada.
Antes de continuar con la forma que van a tener estas ranuras y las consideraciones que vamos a tener en cuenta,
tenemos que calcular el dato fundamental que nos falta, ya que ahora en la ecuación de igualdad de volumen de
viruta no tenemos más incógnitas, por tanto sustituimos para hallar la profundidad de corte que tendremos que
aplicar en torneado:
1000 150,796  a p 
0,2  
12  l  mm 3 
2 


60
0,2  0,6277
 mm 3  1  min 
 seg 
2 
 
 

  60  

seg
800
rev


 min 


2 
0,6277
a p  0,6365 mm
(13)
Teniendo en cuenta que en torneado se suele programar en diámetros, la profundidad de corte será 1,273 mm.
Consideraciones Sobre el Ángulo Evolvente θmáx
Anteriormente hemos dicho que las franjas las vamos a hacer por medio de una fresa de diámetro 18 mm, por
tanto, según vayamos profundizando en la pieza veremos que la magnitud de 18,831 mm perteneciente a la zona
de las franjas hueco se mantendrá constante al serlo el diámetro de la fresa, en cambio, las franjas de material
irán disminuyendo su longitud. Por lo tanto, el ángulo θ que abarcará cada franja de material dejará de ser de 36º,
pasando a ser un valor menor, y esta variación se verá reflejada en el ángulo θmáx del fresado. De esta forma
aprovechamos un solo tocho de material para hacer diferentes ensayos para diferentes θmáx.
Comiendo profundidades 1,2745 mm, para hallar el valor de la θmáx en cada pasada tendremos que hacer el
proceso inverso al realizado para hallar el valor de θ del ángulo que abarcaba la ranura, ahora tendremos que
calcular el valor de θmáx a partir de que sabemos que la anchura de las ranuras y hueco es fija, es decir, conocido
θ.
Por tanto, teniendo en cuenta que se cumple:
Lc    d t
(14)
La longitud de cada tramo de ranura de material será por tanto:
l arco 
Y sabiendo que larco=θ·r tendremos:
  d t  18,831 5
5
(15)
I.Ansoategui et al. / XVIII Congreso Nacional de Ingeniería Mecánica (2010)

l arco 2  l arco

r
d

6
2    d t  188,31
5  dt
(16)
Ya tenemos una relación entre el valor de θ y el valor del diámetro para el tocho cilíndrico. Ahora sólo nos falta
llevar esta relación para saber a que θmáx corresponde cada valor del de θ. Realmente deberíamos de usar ahora la
fórmula completa que relacionaba longitudes de corte en torneado y fresado, pero para simplificar los cálculos
podemos usar la fórmula aproximada:
d t    d f  max
 max 
d t 
df
 max 
2    d  188,31
5d f
(17)
Ahora, si tenemos en cuenta el valor de ap calculado, calcularemos los diferentes valores de θmáx para diferentes
valores del diámetro, y por tanto, de esta forma conseguiremos analizar como varían las temperaturas con el
valor del ángulo evolvente.
1ª pasada => d = 58,7255 → θmáx = 712.53º
2ª pasada => d = 57,4510 → θmáx = 164.88º
3ª pasada => d = 56,1765 → θmáx = 157,24º
4ª pasada => d = 54,9020 → θmáx = 149,59º
5ª pasada => d = 53,6275 → θmáx = 141,94º
6ª pasada => d = 52,3530 → θmáx = 134,29º
7ª pasada => d = 51,0785 → θmáx = 126,64º
8ª pasada => d = 49,8040 → θmáx = 118,99º
9ª pasada => d = 48,5295 → θmáx = 111,34º
10ª pasada => d = 47,2550 → θmáx = 103,69º
11ª pasada => d = 45,9805 → θmáx = 96,037º
12ª pasada => d = 44,7060 → θmáx = 88,387º
Las franjas que realicemos tendrán una profundidad finita. Vamos a hacer franjas de 0,75 mm de profundidad,
por lo tanto, para los datos que hemos obtenido tendremos que podemos llegar para esta profundidad hasta la 11ª
pasada para obtener un corte interrumpido.
Tendremos que calcular su correspondiente velocidad de corte, sabiendo que la velocidad de giro es constante y
su valor conocido.
Además de esto es necesario que tengamos en cuenta el tiempo que cuesta mecanizar una de estas franjas. Para
ello no tenemos más que hacer una regla simple que aplicaremos de forma aproximada a la primera pasada.
Siendo 800 revoluciones por minuto la velocidad de giro, y las ranuras ocupan 1/10 parte de la revolución:
t
60
 0,0075 seg
800 10
(18)
ESTABILIZACIÓN DE LA TEMPERATURA
Para explicar este fenómeno es necesario que realicemos un balance de calor en la zona de corte. Tenemos que
tener en cuenta que el calor que se genera por cizalladura del material en el proceso de corte, se transmite una
parte por conducción a la pieza y otra parte por convección al medio ambiente. Por lo tanto, dentro de la
generación de calor tendríamos dos casos, uno el del corte interrumpido, y otro el del corte continuo. Tenemos
que tener en cuenta que cuando estamos realizando un corte interrumpido, sólo estamos generando calor durante
unos intervalos de tiempo, mientras que en el corte continuo esta generación de calor es constante y tiene un
valor determinado.
Ahora tenemos que ver como se produce la evacuación de calor, para así explicar el porqué de la estabilización
de la temperatura. Este calor será evacuado por medio de conducción a la herramienta y a la pieza, además del
calor que se vaya con la viruta.
Si suponemos una situación en la que hayamos llegado a la estabilización de la temperatura, tendremos que la
fórmula que gobierna este proceso es:
Simulación de fresado mediante corte interrumpido en torno para medición de temperaturas en la herram.
  
  
  Qv
  2  A2  
Q  1  A1  
 x2 
 x1 
7
(19)
Donde:
Q = calor generado en el instante t,
λ1 = coeficiente de conducción del material de la herramienta,
λ2 = coeficiente de conducción del material de la pieza, A1 = superficie de evacuación del calor en
  
  gradiente de temperaturas en la
la herramienta, A2 = superficie de evacuación del calor en la pieza, 
 x1 
  
  gradiente de temperaturas en la pieza y, Qv = calor evacuado por la viruta.
 x2 
herramienta, 
Método Analítico de Cook
Cook desarrolló en 1973 una fórmula que puede ser utilizada para predecir el incremento de temperatura en la
interfase herramienta viruta durante el proceso de maquinado.
U  v  t0 
T  0,4 


 C  K 
0 , 333
Donde: T: temperatura media en la interfase viruta-herramienta (ºC), U: energía específica de la operación
N  m / mm  , v: velocidad de corte (m/s) y,
3
específico volumétrico del material
t 0 : espesor de la viruta antes de corte (m),   C : calor
J


2

 y, K: difusividad térmica del material de trabajo m / s  .
3
 mm º C 
Al incremento de temperatura obtenido por esta ecuación debe sumarse la temperatura de referencia, que será
normalmente la temperatura ambiente, es decir:
T VC   T VC   TReferencia
(20)
Donde:
T = temperatura media del proceso y, TReferencia = temperatura de referencia (normalmente la ambiental).
Si ahora aplicamos la expresión de Cook para los parámetros de los ensayos realizados, podríamos hacernos una
idea de la temperatura que deberíamos de haber obtenido para el caso de corte continuo.
Los parámetros del aluminio Al-2030 T4 son:
U  0,56 Nm / mm 3 , v  2,46m / s,   2,75 g / cm 3 , c  0,882 J / g º C , y   159W / mK
Por lo tanto, si ahora sustituimos los valores anteriores en la expresión de Cook obtenemos que:
∆T = 266 ºC
Si ahora a esto le añadimos la temperatura de referencia:
T VC   T VC   TReferencia  266  20  286º C
Los valores del acero 40NiCrMo7 (AISI 4340, F 1272) son:
U  3,61Nm / mm 3 , v  2,46m / s,   9 g / cm 3 , c  0,507 J / g º C , y   44,5W / mK
Por lo tanto, si ahora sustituimos los valores anteriores en la expresión de Cook y le añadimos la temperatura de
referencia:
T VC   T VC   TReferencia  1833  20  1853º C
I.Ansoategui et al. / XVIII Congreso Nacional de Ingeniería Mecánica (2010)
8
Si comparamos por tanto estos resultados con los obtenidos en los ensayos se puede observar que son bastante
diferentes. Aquí por lo tanto podemos observar el efecto tan importante de la colocación del termopar a una
distancia de 0,5 mm de la cara de desprendimiento.
ENSAYOS REALIZADOS
La consecución de este trabajo precisa de una serie de ensayos experimentales. Por lo tanto, lo que haremos a
continuación será presentar algunos de los resultados obtenidos en estos ensayos mediante el uso de gráficas
Tiempo - Temperatura para cada uno de los diferentes tipos de ensayos realizados a cabo.
Además de esto, tenemos que tener en cuenta que cada uno de los ensayos ha sido realizado a diferentes tiempos
de muestreo, pero para ensayos similares usaremos el mismo tiempo de muestreo.
Como los 75 ms de tiempo de muestreo es algo bajo para tomarlo como para este tipo de ensayos, lo mejor es
que tomemos un tiempo múltiplo de este, por ejemplo, podemos medir la temperatura que tenemos en la cara de
desprendimiento cada 10 vueltas del tocho, es decir, tomaremos un tiempo de muestreo de 750 ms, que es un
tiempo más adecuado. Al estar realizando estos ensayos durante 240 mm de tocho, tendremos que el tiempo total
de muestreo de temperaturas será de 90 segundos.
1ª Pasada
2ª Pasada
3ª Pasada
4ª Pasada
5ª Pasada
6ª Pasada
7ª Pasada
8ª Pasada
9ª Pasada
10ª Pasada
N
(rev/min)
800
800
800
800
800
800
800
800
800
800
Tabla 1 .Resumen De Los Ensayos Realizados
D
Vc
Lc
(mm)
(m/min)
(mm)
58,727
147,597
240
57,450
144,398
240
56,18
141,199
240
54,91
138,006
240
53,64
134,8
240
52,36
131,602
240
51,09
128,402
240
49,82
125,203
240
48,54
122,004
240
47,27
118,795
240
θmáx Fresado
(º)
172,53
164,88
157,24
149,59
141,94
134,29
126,64
118,99
111,34
103,69
Ahora nuestro objetivo será comparar los gráficos para así poder llegar a conclusiones sobre el efecto de la
acción de cada uno de los parámetros que intervienen en el corte.
Gráficos Comparativos A Inmersión Constante
En este apartado veremos los gráficos comparativos que se obtienen, en este caso cuando mantenemos constante
la inmersión y variando cada una de las condiciones de corte anteriormente descritas, es decir, en seco, con MQL
y con taladrina.
Aluminio Corte Interrumpido
80
70
60
Temperatura (ºC)
50
40
Seco
MQL
Taladrina
30
20
10
0
0
10
20
30
40
50
60
70
Tiempo (s)
Fig. 3 y Fig. 4. Gráficos de los ensayos con aluminio mediante corte continuo e interrumpido
80
90
100
Simulación de fresado mediante corte interrumpido en torno para medición de temperaturas en la herram.
9
Gráficas De Los Ensayos Longitud - Temperatura
Aluminio Seco Continuo
300
250
250
200
200
Longitud (mm)
Longitud (mm)
Aluminio Seco Interrumpido
300
150
150
100
100
50
50
0
0
0
10
20
30
40
50
60
70
Temperatura (ºC)
80
0
10
20
30
40
50
60
70
80
Temperatura (ºC)
Fig. 5 y Fig. 6. Gráficos de los ensayos Longitud- Temperatura
ANÁLISIS DE RESULTADOS
Algunos Análisis Gráficas Tiempo y Temperatura
En cuanto a los gráficos comparativos a inmersión constante en aluminio, la taladrina se presenta como la mejor
forma de refrigeración, por delante del método MQL para estas condiciones de corte. Descenso de un 50% en la
temperatura con taladrina, frente a un 22% con MQL.
Por otro lado, en cuanto a los gráficos comparativos a inmersión constante en acero las temperaturas de
estabilización son mayores que en el caso del aluminio debido a que éste tiene mayor punto de fusión y soporta
mejor el calor.
En corte interrumpido se observa que las mayores temperaturas están para el aluminio seco, en torno a (18-75
ºC), para el MQL entre (16-61 ºC) y para la taladrina (17-40 ºC), teniendo como consecuencia que es la taladrina
el mejor refrigerante.
En cambio, en corte continuo se observa que las mayores temperaturas están para el aluminio seco, en torno a
(18-95 ºC), para el MQL entre (22-76 ºC) y para la taladrina (16-45 ºC), teniendo como consecuencia, como
antes, que es la taladrina el mejor refrigerante.
Análisis Gráficas Longitud y Temperatura
En corte interrumpido del aluminio en seco, se produce un incremento de la temperatura hasta llegar a la mitad
del tocho, en la cual los valores rondan entre 60-70 ºC, produciéndose una estabilización de la temperatura ya
que las variaciones que se producen son muy pequeñas.
Por otro lado, en corte continuo en seco del aluminio, hay un aumento progresivo de la temperatura hasta la
mitad de la pieza, en la cual los valores rondan entre 80-100 ºC, produciéndose una estabilización de valores.
Mecanizado interrumpido del aluminio con taladrina, obtenemos un aumento hasta los 100 mm rondando
temperaturas ente 35 y 40 ºC, luego se mantienen prácticamente constante, temperaturas más bajas respecto al
seco y al MQL, porque la taladrina es mejor refrigerante y reduce muchísimo tanto la fricción como el
rozamiento.
Para el acero las conclusiones son las mismas, con la única diferencia que las temperaturas son mayores ya que
tiene un mayor punto de fusión que el aluminio.
CONCLUSIONES
1.
La ley de Cook nos demuestra que las temperaturas obtenidas no son reales por la distancia de 0,5 mm
del termopar a la cara de desprendimiento de la plaquita, a pesar de lo cual, no invalida las
conclusiones anteriores.
90
100
I.Ansoategui et al. / XVIII Congreso Nacional de Ingeniería Mecánica (2010)
10
2.
En los ensayos comparativos a inmersión constante, se observa que la taladrina se presenta como el
mejor refrigerante, por delante del MQL.
3.
Observamos que en cada pasada el tiempo de corte va aumentando, mientras que la velocidad también
disminuye, se trata de algo totalmente lógico, ya que para calcular el tiempo de corte usamos la
longitud de corte, y esta va disminuyendo en cada pasada, lo mismo sucede con la velocidad de corte.
4.
En los ensayos comparativos interrumpido-continuo, se observa que el tiempo de estabilización de la
temperatura depende del tiempo de corte, y no de la cantidad de material cortado, dependerá del
gradiente de temperaturas.
5.
Además se observa que la temperatura de estabilización no se hace la mitad al cortar la mitad de
material, sino que presenta una disminución de aproximadamente 1/5 respecto a la temperatura inicial
debido a que durante el corte interrumpido cortamos y paramos dando lugar a que la herramienta se
enfríe, mientras que en el continuo eso no sucederá ya que lo realizamos sin detenerse.
REFERENCIAS
[1] J. Peláez Vara, El torno. Colección “La Máquina Herramienta” (TOMO I), CEDEL, Barcelona, (1992).
[2] Shaw M.C., Metal Cutting Principles, Oxford Science Publications, (1989).