Estrategia didáctica para la comprensión de los objetivos básicos

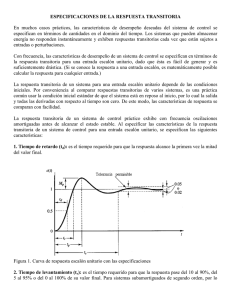
Estrategia didáctica para la comprensión
de los objetivos básicos del análisis y
diseño de sistemas de control
Darío Weitz
Resumen
Se presenta una estrategia didáctica consistente en la utilización de un software educativo que permite una adecuada comprensión de los conceptos de estabilidad absoluta, error en estado estacionario y respuesta transitoria en
el análisis y diseño de sistemas de control. El software puede ser utilizado en cursos introductorios de Teoría de
Control en cualquier carrera de ingeniería.
Palabras clave: estrategia didáctica, análisis y diseño de sistemas de control, ingeniería.
Abstract
A teaching strategy based on an educational software allows a proper understanding of the concepts of absolute
stability, steady state error and transient response in control system analysis and design. The software can be used
in introductory courses in control theory at any engineering school.
Keywords: teaching strategy, control system analysis and design, engineering.
Introducción
El análisis y el diseño de un sistema de control incluyen la capacidad de predecir el comportamiento dinámico del
sistema físico a controlar a partir del conocimiento de los distintos componentes que lo conforman. Tres son los
objetivos básicos del análisis y diseño de un sistema de control: garantizar la estabilidad absoluta, reducir o eliminar el error en estado estacionario y producir una respuesta transitoria satisfactoria (Nise, 2006).
Un sistema de control lineal e invariante en el tiempo es inestable si su respuesta libre (la que depende solo del
sistema y no de la entrada) crece sin límite a partir de su estado de equilibrio cuando el sistema está sujeto a cierto
tipo de entrada. Conceptualmente, la respuesta del sistema debe estar entre las siguientes alternativas: estable,
críticamente estable o inestable.
El error en estado estacionario es la diferencia entre la entrada y la salida para una entrada de prueba preestablecida
conforme el tiempo tiende a infinito. Si no hay una coincidencia exacta entre la entrada en estado estacionario y
la salida en el mismo estado, se afirma que el sistema presenta un error en estado estacionario. Es un objetivo que
apunta a establecer la exactitud de la respuesta y cuya valor cuantitativo puede ser tolerado o no según las características y usos finales del sistema físico que se está controlando.
El tercer objetivo básico es la respuesta transitoria. Está relacionada con la forma en que el sistema físico adquiere
o disipa energía. Las inercias que poseen los sistemas físicos reales les impiden cambiar sus estados en forma instantánea, y por lo tanto las salidas difieren de las entradas durante el período transitorio. Las respuestas transitorias
varían en forma significativa según el orden de sistema y según la entrada a la cual está siendo sometido el mismo.
Existen diversas medidas de desempeño que permiten cuantificar la calidad de la respuesta transitoria.
Cualquier curso que aspire a proporcionar los principios básicos de los sistemas de control automático –ya se trate
de control clásico, control en el espacio de estado o control en tiempo discreto– debe obligatoriamente incluir
Autor: El autor es Ingeniero Químico y Profesor Asociado de la Cátedra de Teoría de
Control en el Departamento Ingeniería en Sistemas de Información. Facultad Regional
Rosario, Universidad Tecnológica Nacional.
Dirección de contacto: darweitz@yahoo.com.ar
Revista Argentina de Enseñanza de la Ingeniería / Año 4 / Nº 8 / Abril 2015
41
Desarrollo de experiencias didácticas con carácter innovador en la enseñanza de grado
los tres objetivos básicos previamente citados. Existe una abundante bibliografía que los incluye (Coughanowr, 1991; Kuo, 1996; Ogata, 1996; Ogata, 2003;
Nise, 2006). Sin embargo, la extensión de la citada bibliografía y la profusión de
ejemplos de sistemas físicos asociados a otras carreras de ingeniería dificultan su
utilización en un curso de duración cuatrimestral en la carrera de Ingeniería en
Sistemas de Información.
Una estrategia didáctica para permitir un tratamiento comprensible y rápido de
los objetivos básicos del análisis y diseño de un sistema de control consiste en la
utilización de un software educativo orientado a mostrar cómo diferentes señales
de prueba aplicadas a sistemas de primer y segundo orden permiten una adecuada
comprensión de los conceptos de estabilidad absoluta, error en estado estacionario
y respuesta transitoria.
Existen poderosos lenguajes científicos de alto nivel tales como MATLAB®
(Mathworks®, 2013) que incluyen toolboxes utilizados con fines educativos, de
investigación y desarrollo y para aplicaciones de control industrial. Sin embargo,
los mismos tienen como desventajas el no ser gratuitos, una programación orientada a matrices y, principalmente, mostrar importantes limitaciones al momento en
que el docente debe explicar los conceptos subyacentes en los principios básicos
de los sistemas de control automático. Existe software didáctico orientado al diseño y análisis de sistemas de control lineal (Gómez Cadavid, 2009; Dormido et al.,
2012), pero son herramientas basadas en Matlab o en lenguajes compatibles con
Matlab, por lo cual se mantienen las limitaciones definidas previamente.
En el presente trabajo se describen las características de un software educativo
diseñado como herramienta de apoyo para introducir los conceptos básicos de los
sistemas de control en tiempo continuo, y se detallan las ventajas de su utilización
en un curso de la asignatura Teoría de Control para alumnos de cuarto año de la
carrera de Ingeniería en Sistemas de Información.
Análisis de la estrategia didáctica
La carrera de Ingeniería en Sistemas de Información de la Universidad Tecnológica Nacional tiene a la asignatura Teoría de Control en el primer cuatrimestre del cuarto año del Plan de Estudios vigente. Los contenidos básicos incluyen:
introducción a los sistemas de control automático; análisis y diseño de sistemas
de control en tiempo continuo; introducción a los sistemas de control en tiempo
discreto; control en el espacio de estados. El curso aspira a proporcionar la base
conceptual de los principios de la Teoría de Control con vistas a adquirir destrezas
en el análisis y diseño de los sistemas de control automático.
Los docentes de la cátedra de Teoría de Control se encuentran, al momento de
satisfacer los requerimientos del Plan de Estudios, con tres restricciones muy importantes: i) la carga horaria total de la asignatura es de 96 horas cátedra; ii) los
alumnos llegan al cursado de la asignatura sin las destrezas necesarias para desarrollar de manera rápida los modelos matemáticos de sistemas físicos habitualmente analizados durante los cursos de Teoría de Control; iii) los alumnos llegan
al cursado de la asignatura sin conocimientos previos de MATLAB®.
Tras varios años de cursos no cumplimentados en forma satisfactoria, se decidió
desarrollar un software educativo que pudiera ser utilizado como apoyo a la tarea
docente en el aula. La primera etapa del citado software tiene como propósito presentarle a los alumnos un tratamiento comprensible y rápido de los tres objetivos
básicos en el análisis y diseño de un sistema de control: estabilidad absoluta, error
en estado estacionario y respuesta transitoria.
Software educativo
El software educativo fue desarrollado utilizando el lenguaje de programación C#.
Es un lenguaje de programación de propósito general orientado a objetos desarrollado y estandarizado por Microsoft como parte de su plataforma .NET. Es un
42
Revista Argentina de Enseñanza de la Ingeniería / Año 4 / Nº 8 / Abril 2015
Desarrollo de experiencias didácticas con carácter innovador en la enseñanza de grado
lenguaje diseñado para la infraestructura de lenguaje común (Common Language
Infrastructure, CLI), una especificación estandarizada que describe un entorno virtual para la ejecución de aplicaciones; tales aplicaciones, aunque estén escritas en
diferentes lenguajes de alto nivel, pueden ejecutarse en diversas plataformas tanto
de software como de hardware sin la necesidad de volver a compilar el código
fuente (Kimmel, 2002).
Para la construcción de gráficos y curvas se utilizó la librería ZedGraph. Se trata de
una librería de clases, control de usuario y control web escrita en C# que permite
crear gráficas en proyectos .NET (Licencia: GNU Library o Lesser General Public
License).
El sistema software está compuesto por varios módulos correspondientes a cada
proyecto educativo. Los módulos incluyen: respuesta transitoria de sistemas de
primer y segundo orden a una entrada escalón; respuesta de sistemas de primer y
segundo orden a una entrada senoidal; ubicación de las raíces y respuesta al impulso; respuesta de sistemas de primer y segundo orden a una entrada rampa.
Señales de entrada
Las señales de entrada (señales de prueba) que se utilizan habitualmente en el
estudio de sistemas de control comprenden a las siguientes funciones: escalón,
impulso, senoidal, rampa y parábola.
La señal de tipo escalón se utiliza para cuantificar la calidad de la respuesta transitoria a través de diferentes medidas de desempeño. La respuesta transitoria de
los sistemas de primer orden se evalúa mediante el tiempo de subida (tiempo de
levantamiento, rise time) y el tiempo de asentamiento (tiempo de establecimiento,
settling time). La respuesta transitoria de los sistemas de segundo orden subamortiguados se evalúa mediante el tiempo de subida, tiempo del primer pico (peak
time), sobreimpulso (sobrepaso máximo, overshoot), razón de caída (decay ratio),
tiempo de asentamiento y número de oscilaciones.
La señal de tipo impulsiva (respuesta al impulso) permite analizar la estabilidad
absoluta de un sistema a partir de la ubicación de las raíces de la ecuación característica. En el caso de raíces reales, la respuesta es una exponencial creciente si el
valor de la raíz es positivo o decreciente si es negativo. En el caso de raíces complejas conjugadas, la respuesta es una senoidal amortiguada cuando la parte real
de la raíz es negativa o una senoidal creciente cuando la parte real es positiva; la
frecuencia de oscilación depende del valor de la parte imaginaria de la raíz. En el
caso de raíces complejas imaginarias puras, la respuesta es una senoidal de amplitud constante y de frecuencia igual al valor de la parte imaginaria de la raíz. Si
la raíz está ubicada en el origen y no está repetida, la respuesta es una constante.
La señal de tipo senoidal se emplea para analizar la respuesta de un sistema
lineal e invariante en el tiempo sobre un intervalo de frecuencias. La frecuencia
de entrada se varía desde cero hasta algún valor significativo, representativo
de las características del sistema, y se determinan la relación de amplitud y el
retardo de fase entre la salida y la entrada senoidal. Con los valores calculados,
se dibujan las Trazas de Bode y los Diagramas de Nyquist; a partir de los mismos, se sacan conclusiones sobre la estabilidad absoluta, se puede predecir el
comportamiento transitorio y se determina el margen de ganancia y el margen
de fase.
La señal de tipo rampa se utiliza para analizar cómo responde el sistema a entradas que cambian linealmente con el tiempo (entradas de velocidad constante).
Es una señal no acotada que se emplea además para cuantificar la constante del
error de velocidad o constante de error rampa.
La señal de tipo parabólica es la señal de prueba más rápida que habitualmente
se utiliza en sistemas de control y representa entradas con aceleración constante.
Es una señal no acotada que se emplea además para cuantificar la constante del
error de aceleración o constante de error parabólica.
Revista Argentina de Enseñanza de la Ingeniería / Año 4 / Nº 8 / Abril 2015
43
Desarrollo de experiencias didácticas con carácter innovador en la enseñanza de grado
Módulo respuesta transitoria a una entrada escalón
En el módulo Respuesta Transitoria de Sistemas de Primer Orden, una tabla de ingreso de datos permite incorporar hasta cinco valores para la amplitud del escalón
y para la constante de tiempo. Al cliquear el ícono Graficar se visualizan hasta cinco curvas de salida, cada una de ellas en diferente color. Las curvas se representan
en el eje Tiempo hasta cinco veces el valor de la mayor constante de tiempo. Al
cliquear el ícono Medidas de Desempeño, se muestran los valores calculados del
tiempo de subida y del tiempo de asentamiento para cada curva. Hay cinco casillas
de verificación (check box) que permiten visualizar líneas horizontales y verticales
correspondientes a la amplitud de la entrada, al tiempo de subida, tiempo de asentamiento y tiempo en que la respuesta llega al 63% de su valor final; también se
puede visualizar la pendiente de la curva calculada desde el origen (Fig. 1).
Durante la clase, primero se muestra que al ingresar la misma constante de tiempo
y diferentes amplitudes del escalón, se observa que todas las respuestas llegan al
63% de su valor final cuando el tiempo transcurrido es una constante de tiempo independiente del valor de la amplitud de la entrada escalón; lo anterior implica que
todas las curvas exhiben la misma velocidad de respuesta transitoria. Las mismas
conclusiones se arriban para el tiempo de subida (2.2 veces el valor de la constante
de tiempo) y para el tiempo de asentamiento (4 veces el valor de la constante de
tiempo). Se indica además que toda la información útil de la respuesta está concentrada en el intervalo que va desde el origen hasta cinco constantes de tiempo.
A continuación se muestra que al ingresar la misma amplitud del escalón y diferentes constantes de tiempo, se visualiza –y se analiza mediante los valores calculados– como todas las medidas de desempeño indican distintas velocidades de
respuesta según los diferentes valores asignados a las respectivas constantes de
tiempo.
En el módulo Respuesta Transitoria de Sistemas de Segundo Orden, una tabla de
ingreso de datos permite incorporar hasta cinco valores para la amplitud del escalón, constante de tiempo, coeficiente de amortiguamiento y un único valor para
el ancho de la banda que permite calcular el tiempo de asentamiento. Al cliquear
el ícono Graficar se visualizan hasta cinco curvas de salida, cada una de ellas en
diferente color. Las curvas se representan en el eje Tiempo hasta un 10% adicional
al valor del mayor tiempo de asentamiento. Al cliquear el ícono Medidas de Desempeño, se indica si la respuesta es subamortiguada, críticamente amortiguada o
sobreamortiguada. Para los tres tipos de respuesta se muestran los valores de los
correspondientes tiempos de subida y tiempos de asentamiento. Adicionalmente,
para las respuestas subamortiguadas se indican los valores calculados del sobreimpulso, razón de caída, tiempo del primer pico, período de oscilación y número de
oscilaciones. Hay una casilla de verificación para visualizar en pantalla el tiempo
del primer pico con el correspondiente sobreimpulso, y otra casilla que permite
mostrar las bandas (por encima y por debajo del valor final) que delimitan al tiempo de asentamiento (Fig. 2).
Experimentando con diferentes valores de la constante de tiempo y del coeficiente
de amortiguación se pueden observar los distintos tipos de respuesta transitoria,
como así también cómo varían las dos medidas de desempeño más importantes de
este tipo de respuesta –sobreimpulso y tiempo de asentamiento– en función de los
valores de los datos de entrada. Se indica además que toda la información útil de
la respuesta está concentrada en el intervalo que va desde el origen hasta un 10%
adicional al valor del tiempo de asentamiento.
Módulo respuesta a una entrada senoidal
Para visualizar la respuesta de un sistema de primer orden a una entrada senoidal, una tabla de ingreso de datos permite incorporar valores para la constante de
tiempo del sistema, y para el valor base, la amplitud y la frecuencia de la señal de
entrada. Al cliquear el ícono Graficar, se visualiza la entrada, la salida senoidal
44
Revista Argentina de Enseñanza de la Ingeniería / Año 4 / Nº 8 / Abril 2015
Desarrollo de experiencias didácticas con carácter innovador en la enseñanza de grado
estacionaria y la salida total (que incluye al término transitorio que rápidamente se
hace despreciable). Las curvas se representan en el eje Tiempo hasta cuatro períodos para mostrar como la entrada y la salida tienen la misma frecuencia.
Haciendo clic en el icono Medidas de Desempeño se muestran los valores calculados del período de oscilación, el retardo de fase (en unidades de tiempo, radianes
y grados), la relación de amplitud, máximos y mínimos valores de la entrada y de
la salida, el tiempo en que se solapa la respuesta total con la respuesta estacionaria
y una tabla que muestra como varía el retardo de fase (en grados) para diferentes
valores de frecuencia (0,1,2,10,100,1000,∞) para la constante de tiempo ingresada
como dato (Fig. 3). En pantalla se puede observar además el período de oscilación
y el retardo de fase.
La respuesta senoidal de un sistema de segundo orden solo difiere en el ingreso
como dato de un valor para el coeficiente de amortiguamiento, en la posibilidad
de observar una salida amplificada respecto a la entrada, y como el retardo de fase
tiende a -180° con el aumento de la frecuencia.
En el curso se experimenta con numerosos valores de frecuencia, constante de
tiempo y coeficiente de amortiguación (solo en sistemas de segundo orden) y se
analizan los valores calculados de relación de amplitud y retardo de fase. El análisis y discusión de las curvas graficadas y de los valores calculados establece las
bases para introducir los métodos de Respuesta en Frecuencia (Trazas de Bode y
Diagramas de Nyquist), a partir de los cuales se sacan conclusiones sobre la estabilidad absoluta y se puede cuantificar la calidad de la respuesta transitoria.
Módulo respuesta al impulso
Se analiza la estabilidad de un sistema de control a partir de visualizar como cambia la salida después de una entrada impulso según la ubicación de las raíces. El
software muestra un plano complejo con el eje real representado entre -4 y +4,
y el eje imaginario entre -2 y +10. Haciendo clic sobre algún punto del eje real
negativo se visualiza la respuesta exponencial decreciente que corresponde a un
sistema que solo posee un polo negativo. Haciendo clic sobre algún punto del eje
real positivo se visualiza la respuesta exponencial creciente que corresponde a un
sistema que solo posee un polo positivo. Haciendo clic sobre algún punto del eje
imaginario, se visualiza una respuesta periódica no amortiguada. Haciendo clic sobre algún punto del plano que tiene componente real y componente imaginaria, se
visualiza una senoidal creciente o decreciente según el componente real sea positivo o negativo respectivamente. Para cada una de las alternativas citadas, se pueden
graficar hasta cuatro curvas en forma simultánea, como una forma de mostrar la
velocidad de caída o crecimiento (según la distancia al eje imaginario) y/o mostrar
la variación en la frecuencia de oscilación (según la distancia al eje real) (Fig. 4).
Para cada punto cliqueado se muestra el correspondiente valor del coeficiente de
amortiguación y de la frecuencia natural de oscilación y/o constante de tiempo.
Módulo respuesta a una entrada rampa
La respuesta a una entrada rampa, tanto de un sistema de primer orden con ganancia unitaria como así también de un sistema de segundo orden con ganancia unitaria, permite establecer las bases del análisis del error en estado estacionario. En el
módulo donde se desarrolla la respuesta a una entrada rampa, una tabla de ingreso
de datos permite incorporar hasta cinco valores de la pendiente de la rampa o de la
constante de tiempo del sistema. Para un sistema de segundo orden se agrega como
dato el valor del coeficiente de amortiguamiento. Las curvas de salida muestran
como, en la medida en que el término exponencial de la respuesta se va haciendo
despreciable, el error en estado estacionario crece desde un valor inicial nulo hasta
su valor final correspondiente al retraso dinámico definido por la magnitud de la
constante de tiempo del sistema. En las curvas de respuesta de los sistemas de segundo orden subamortiguados, se observa además la clásica respuesta transitoria
Revista Argentina de Enseñanza de la Ingeniería / Año 4 / Nº 8 / Abril 2015
45
Desarrollo de experiencias didácticas con carácter innovador en la enseñanza de grado
de este tipo de sistemas (Fig. 5).
Características del software educativo
Los contenidos del software educativo se proyectan en el aula en formato gigante
mediante una computadora portátil y un proyector apropiado. La interfaz gráfica
es amigable e intuitiva. El ingreso de datos a los módulos es muy simple y rápido:
solo se ingresan valores numéricos o se cliquea en la gráfica exhibida en la pantalla
(respuesta al impulso). Los valores numéricos están validados en lo que respecta
al tipo de dato y al rango que se puede ingresar. Cada pantalla tiene un texto de
identificación que la distingue de las demás para evitar confusiones. Todas las
curvas se grafican en colores diferentes y tienen su leyenda correspondiente para
una apropiada identificación. Se puede almacenar en memoria cualquiera de las
gráficas expuestas en pantalla para su posterior comparación con otros tipos de
respuesta; un botón Comparar permite la visualización de las últimas cuatro pantallas almacenadas.
Varios módulos permiten graficar hasta cinco curvas de manera simultánea, lo cual
permite una rápida y fácil visualización de la influencia del parámetro variado en
la respuesta del sistema. En todos los casos, se procuró maximizar el tamaño de
las gráficas para así resaltar las características específicas de cada respuesta. Los
módulos incluyen un ícono de Medidas de Desempeño donde se resumen los valores calculados más importantes a la hora de interpretar el tipo de respuesta que se
está analizando. En todas las gráficas se puede hacer zoom para analizar en detalle
un sector reducido de la respuesta. También se puede recorrer con el mouse las
curvas mostradas en la pantalla y en un recuadro flotante se indica el tipo de curva
(ie: entrada escalón, salida senoidal estacionaria, salida rampa primer orden) y los
valores de abscisas y ordenadas correspondientes (o valores calculados del coeficiente de amortiguación y de la frecuencia natural de oscilación).
Un conjunto de casillas de verificación específicas para cada módulo permite incorporar (según demanda) información adicional de suma utilidad para los objetivos didácticos. Como ejemplo de lo anterior se puede indicar: líneas horizontales
y verticales que muestran al 63% de la respuesta final en el módulo de respuesta
transitoria de un sistema de primer orden a una entrada escalón; bandas dibujadas
por encima y por debajo del valor final y que permiten delimitar al tiempo de asentamiento en el módulo de respuesta transitoria de un sistema de segundo orden a
una entrada escalón; la respuesta total (que incluye al término transitorio) de un
sistema de primer orden a un entrada senoidal y que permite observar como la
misma se “mezcla” con la respuesta senoidal estacionaria cuando el tiempo transcurrido está próximo a tres veces la constante de tiempo del sistema; la separación
entre la entrada y la salida para las respuestas a la entrada rampa de los sistemas
de primer y segundo orden, como ayuda a visualizar el retraso dinámico que se
traduce en el error en estado estacionario para estos sistemas.
Otra de las ventajas del software es que resulta relativamente sencillo agregar funcionalidades o modificar las existentes. Así, ante dudas surgidas en los alumnos
durante el desarrollo de los temas correspondientes a la respuesta escalón de sistemas de segundo orden, se decidió incorporar un par de botones cuyo cliqueo
permite visualizar como varía el sobreimpulso con el coeficiente de amortiguamiento, como así también como varía el tiempo de asentamiento con el coeficiente
de amortiguamiento, para los criterios de bandas del 2% y del 5% (Fig. 6). Esas
gráficas se incorporaron inmediatamente y las dudas fueron respondidas en forma
satisfactoria en la siguiente clase. Lo mismo sucedió ante una consulta relativa a la
pendiente desde el origen en la respuesta al escalón de un sistema de primer orden.
El software educativo fue empleado en tres cursos de la asignatura durante el primer cuatrimestre del año 2013 y del año 2014. Al final del curso lectivo 2014 se
presentó a los alumnos una encuesta de percepción de utilidad del software. La
encuesta (79 alumnos respondieron a la misma) mostró que el 96% de los alumnos
46
Revista Argentina de Enseñanza de la Ingeniería / Año 4 / Nº 8 / Abril 2015
Desarrollo de experiencias didácticas con carácter innovador en la enseñanza de grado
consideró importante la utilización del software educativo como herramienta didáctica. Quienes se manifestaron en forma más positiva fue un grupo de alumnos
que no habían regularizado la asignatura en cursos anteriores, y por lo tanto pudieron comparar la utilización de la estrategia didáctica con el curso convencional que
se dictaba previamente. Se evaluó la calidad de las gráficas, los textos explicativos,
las tablas de medidas de desempeño y las casillas de verificación. La encuesta
mostró la necesidad de mejorar varios textos explicativos, tanto en tamaño de letra
como en contraste de colores.
Conclusiones
Se desarrolló un software educativo que permite un tratamiento rápido y comprensible de los objetivos básicos del análisis y diseño de un sistema de control. Es un
sistema modularizado que admite el agregado o modificación de funcionalidades.
A partir de una interfaz amigable para el acceso a los módulos y para el ingreso
de datos, le permite al docente desarrollar una importante cantidad de ejemplos
relacionados con las respuestas de sistemas de primer y segundo orden lineales e
invariantes en el tiempo a las entradas habitualmente utilizadas para experimentar
con los sistemas de control.
El software educativo fue utilizado como herramienta de apoyo para introducir
los conceptos básicos de los sistemas de control en tiempo continuo. También se
lo utilizó para responder satisfactoriamente a las habituales dudas que surgen en
los alumnos durante esas clases. Un número significativo de alumnos consultados
afirmó haber aprehendido los conceptos introducidos de manera satisfactoria. El
software demostró ser una herramienta apropiada para propósitos educativos a nivel universitario de grado y puede ser utilizado en cursos introductorios de Teoría
de Control en cualquier carrera de ingeniería.
La siguiente etapa del trabajo comprenderá el desarrollo de módulos orientados a
la enseñanza de los métodos gráficos más utilizados para determinar la estabilidad
de los sistemas de control automáticos: Lugar Geométrico de las Raíces, Trazas de
Bode y Diagramas de Nyquist.
Agradecimientos
Los siguientes alumnos, pertenecientes a la carrera de Ingeniería en Sistemas de
Información de la Facultad Regional Rosario de la Universidad Tecnológica Nacional (Rosario – Argentina), colaboraron en la programación del software educativo descripto en este trabajo: Lucía Conchillo, Leandro Chavarri, Franco Dipre, Natanael Fiorilla, Franco Lazaro, Leandro Lisa, Federico Maccaroni, Mauro
Manavella, Benjamín Masello, Gabriel Maurino, Guido Moyano, Luís Pagliaro,
Nicolás Román y Franco Sabino.
Referencias bibliográficas
COUGHANOWR, D. (1991) Process System Analysis and Control. 2a edición.
Mc Graw Hill. New York.
DORMIDO, S., GUZMÁN, J.L., COSTA-CASTELLO, R., BERENGUEL, M.
(2012) Interactividad en control automático: fundamentos y experiencias, Memoria XV Congreso Latinoamericano de Control Automático, 23–26 octubre, Lima,
Perú.
GÓMEZ CADADIV, J. C. (2009) Toolbox didáctico para el diseño y análisis de
sistemas de control lineal, Revista Educación en Ingeniería, 8, 155 -169.
KUO, B. (1993) Sistemas de Control Automático. 7a edición. Prentice Hall Hispanoamericana. México.
KIMMEL, P. (2002) Advanced C# Programming. 1a edición. Mc Graw Hill/Osborne. New York.
MATHWORKS® (2013) Recuperado el 15 de mayo de 2013 de http://www.
mathworks.com/products/matlab/
Revista Argentina de Enseñanza de la Ingeniería / Año 4 / Nº 8 / Abril 2015
47
Desarrollo de experiencias didácticas con carácter innovador en la enseñanza de grado
NISE, N. (2006) Sistemas de Control para Ingeniería. 3a edición. Compañía Editorial Continental. México.
OGATA, K. (2003) Ingeniería de Control Moderna. 4a edición. Pearson Educación. Madrid.
OGATA, K. (1996) Sistemas de Control en Tiempo Discreto. 2a edición. Prentice
Hall Hispanoamericana. México.
Fig.1: Respuesta transitoria de un sistema de primer orden a una entrada escalón
Fig. 2: Respuesta transitoria de un sistema de segundo orden a una entrada escalón
48
Revista Argentina de Enseñanza de la Ingeniería / Año 4 / Nº 8 / Abril 2015
Desarrollo de experiencias didácticas con carácter innovador en la enseñanza de grado
Fig. 3: Respuesta de un sistema de primer orden a una entrada senoidal
Fig. 4: Ubicación de las raíces y respuesta a una entrada impulso
Fig. 5: Respuesta de un sistema de segundo orden a una entrada rampa
Revista Argentina de Enseñanza de la Ingeniería / Año 4 / Nº 8 / Abril 2015
49
Desarrollo de experiencias didácticas con carácter innovador en la enseñanza de grado
Fig. 6: Variación del tiempo de asentamiento con el coeficiente de amortiguamiento
50
Revista Argentina de Enseñanza de la Ingeniería / Año 4 / Nº 8 / Abril 2015