MUESTRA M1a M1b M2a M3a M3b M3c M3d

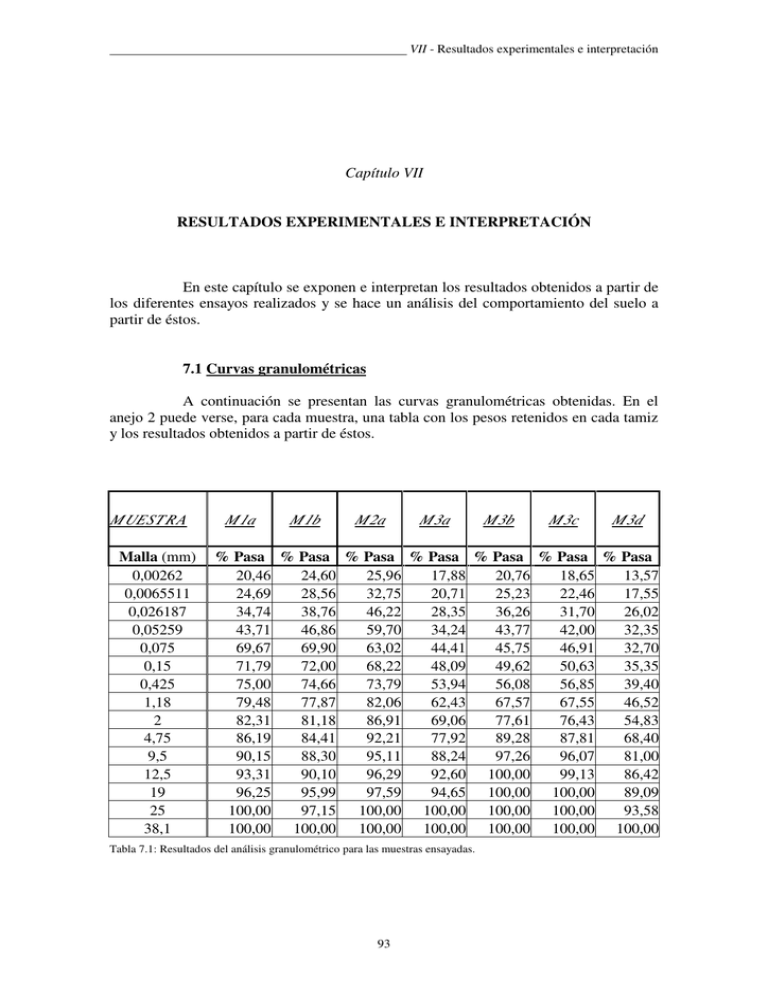
VII - Resultados experimentales e interpretación
Capítulo VII
RESULTADOS EXPERIMENTALES E INTERPRETACIÓN
En este capítulo se exponen e interpretan los resultados obtenidos a partir de
los diferentes ensayos realizados y se hace un análisis del comportamiento del suelo a
partir de éstos.
7.1 Curvas granulométricas
A continuación se presentan las curvas granulométricas obtenidas. En el
anejo 2 puede verse, para cada muestra, una tabla con los pesos retenidos en cada tamiz
y los resultados obtenidos a partir de éstos.
M UEST R A
Malla (mm)
0,00262
0,0065511
0,026187
0,05259
0,075
0,15
0,425
1,18
2
4,75
9,5
12,5
19
25
38,1
M 1a
M 1b
M 2a
M 3a
M 3b
M 3c
M 3d
% Pasa % Pasa % Pasa % Pasa % Pasa % Pasa % Pasa
20,46
24,60
25,96
17,88
20,76
18,65
13,57
24,69
28,56
32,75
20,71
25,23
22,46
17,55
34,74
38,76
46,22
28,35
36,26
31,70
26,02
43,71
46,86
59,70
34,24
43,77
42,00
32,35
69,67
69,90
63,02
44,41
45,75
46,91
32,70
71,79
72,00
68,22
48,09
49,62
50,63
35,35
75,00
74,66
73,79
53,94
56,08
56,85
39,40
79,48
77,87
82,06
62,43
67,57
67,55
46,52
82,31
81,18
86,91
69,06
77,61
76,43
54,83
86,19
84,41
92,21
77,92
89,28
87,81
68,40
90,15
88,30
95,11
88,24
97,26
96,07
81,00
93,31
90,10
96,29
92,60 100,00
99,13
86,42
96,25
95,99
97,59
94,65 100,00 100,00
89,09
100,00
97,15 100,00 100,00 100,00 100,00
93,58
100,00 100,00 100,00 100,00 100,00 100,00 100,00
Tabla 7.1: Resultados del análisis granulométrico para las muestras ensayadas.
93
VII - Resultados experimentales e interpretación
Curvas granulométricas // M1a - M1b
10 0
90
80
70
60
50
40
30
20
10
0
0 ,0 0 1
0 ,0 1
0 ,1
1
10
10 0
O b e rt u ra m a lla ( m m )
M 1a
M 1b
Figura 7.1: Curvas granulométricas - muestras M1.
Curva granulométrica M2a
10 0
90
80
70
60
50
40
30
20
10
0
0 ,0 0 1
0 ,0 1
0 ,1
1
10
10 0
O b e rt u ra m a lla ( m m )
Figura 7.2: Curva granulométrica - muestra M2a.
Curvas granulométricas // M3
10 0
90
80
70
60
50
40
30
20
10
0
0 ,0 0 1
0 ,0 1
0 ,1
1
10
O b e rt u ra m a lla ( m m )
M3a
M3b
Figura 7.3: Curvas granulométricas - muestras M3.
94
M3c
M3d
10 0
VII - Resultados experimentales e interpretación
A continuación se presentan las curvas granulométricas de todas las
muestras ensayadas juntas en una misma gráfica.
Curvas granulométricas
10 0
90
80
70
60
50
40
30
20
10
0
0 ,0 0 1
0 ,0 1
0 ,1
1
10
10 0
Obe rtura ma lla (mm)
M 1a
M2a
M3a
M3b
M3c
M 1b
M3d
Figura 7.4: Curvas granulométricas de todas las muestras ensayadas.
7.2 Interpretación de los resultados del análisis granulométrico.
En las curvas granulométricas (figuras 7.1 a 7.4) se observa la buena
graduación del suelo para todas las muestras, aunque se observan diferencias entre las
mismas.
Las muestras M1 presentan un pequeño salto de la curva, lo que indica que
este suelo se compone de partículas de dos tamaños bien diferenciados, aunque dentro
de cada uno de estos tamaños existe una variación de los mismos.
La muestra M2 es la que contiene un porcentaje mayor de materiales finos
lo que puede dar lugar a bajas resistencias.
Las muestras M3 contienen un gran porcentaje de materiales gruesos; es un
suelo muy bien graduado al igual que la muestra M2.
En el anejo 1 se muestra la posición de las muestras bloques a partir de las
que se ha trabajado y en la figura 7.5 se observa, de manera aproximada, la cercanía de
las mismas al substrato rocoso subyacente (pizarras del Paleozoico), importante para la
interpretación de los resultados obtenidos.
Según el corte geológico del solar adjunto en el anejo 1 (Bosch & Ventayol,
2000), el substrato de pizarras y esquistos sobre el que se encuentra el material
cuaternario que se ha ensayado se puede diferenciar en dos zonas; una donde la roca se
encuentra muy fracturada y plegada y la otra más superficial, muy fracturada y plegada
también y superficialmente alterada que presenta carbonataciones blanquecinas. Esto
favorece la disgregación de la roca más fácilmente en superficie.
95
VII - Resultados experimentales e interpretación
Las muestras M1 fueron tomadas frente a la pantalla número ocho, es decir,
en la zona en la que se realizó el sondeo número dos (ver posición en planta en el anejo
1), a 8 metros de profundidad respecto la cota original del solar. La marcada
bimodalidad de las poblaciones indica la cercanía del substrato al Cuaternario en la zona
de la toma de las muestras.
Las muestras M2, en cambio, fueron tomadas frente a la pantalla número
siete (ver posición en planta en el anejo 1). La muestra fue tomada a 4,5 metros de
profundidad donde únicamente encontramos cuaternario (figura 7.5). De aquí que esta
muestra presente una mayor cantidad de partículas finas mientras que las partículas
gruesas que aparecen se encuentran en menor proporción que las primeras.
La presencia de partículas de mayor tamaño en las muestras M3 indica la
proximidad de éstas a la roca sobre la que se encuentran (pizarras del Paleozoico). Las
muestras M3 fueron tomadas a 7,5 metros de profundidad respecto la cota original del
solar frente a la pantalla número ocho, es decir en la misma posición que las muestras
M1 pero a menor profundidad.
Tras estos resultados obtenidos las muestras M2 y las muestras M3
presentan una coherencia en sus granulometrías frente su posición relativa respecto el
substrato rocoso subyacente. Cuanto más cerca están de la roca mayor es su contenido
en gruesos. No obstante, las muestras M1 obtenidas a la mayor profundidad, y por tanto
las más cercanas a la roca, presentan una clara bimodalidad pero no mayor contenido en
gruesos que la muestra M3. De modo que dentro de la homogeneidad del material puede
concluirse que presenta ciertas discontinuidades localizadas.
96
VII - Resultados experimentales e interpretación
Figura 7.5: Profundidad de las muestras bloque. Corte geológico de Bosch & Ventayol (2000).
97
VII - Resultados experimentales e interpretación
7.3 Límites de Atterberg.
En la tabla 7.2 pueden observarse los valores obtenidos para cada límite en
las diferentes muestras ensayadas. El límite líquido está muy próximo a 50 para las
muestras M1, mientras que para las muestras M2 y M3 este valor disminuye a 34 y 35
como valores medios. El límite plástico en cambio varía entre 23 para las muestras M1,
18 para la M2 y 20 como valor medio para las muestras M3.
Debe advertirse que el límite líquido obtenido para las muestras M1 es muy
elevado. Esto indica que las partículas que componen el suelo son muy finas, es decir,
son partículas arcillosas que retienen mucho el agua. Esto implica un elevado índice de
plasticidad. A medida que el índice de plasticidad disminuye, muestras M2 y M3, las
partículas son más limosas.
La información recopilada inicialmente (Bosch & Ventayol, 2000) indica
una coherencia en los resultados obtenidos en este apartado para las muestras M2 y M3.
Deben tratarse con prudencia los valores obtenidos para las muestras M1 ya que no se
mantienen en la línea esperada.
98
VII - Resultados experimentales e interpretación
7.4 Propiedades básicas del suelo.
A partir de los datos obtenidos en el laboratorio, especialmente de la
humedad (w) y la densidad de las partículas sólidas (γS), se obtiene los parámetros
característicos del suelo ensayado que se denominan propiedades básicas del suelo.
La humedad, definida como el peso del agua dividido por el peso del suelo
seco, se obtiene tomando una muestra de suelo, en el proceso de tallado de las probetas
por ejemplo, se pesa junto en un cuenco tarado y se seca al horno a 100 °C durante 24
horas. La diferencia de los pesos obtenidos antes y después del secado es el peso del
agua que contiene la muestra y de este modo se calcula la humedad mediante la
expresión 7.1:
ω=
Wω
×100
Ws
(7.1)
El peso específico de las partículas sólidas se ha considerado γS = 2,65
g/cm debido a experiencias anteriores en suelos estudiados en la misma zona.
3
Estos parámetros definidos en los párrafos anteriores pueden conocerse
independientemente del valor del volumen de suelo ensayado. En cambio sólo se puede
conocer el peso específico natural (γn) en aquellas muestras con las que se haga una
probeta para su ensayo en el aparato triaxial o el triaxial de columna resonante.
Veamos primero aquellas muestras en las que el volumen de suelo ensayado
es conocido.
Conocido entonces el volumen de suelo a ensayar se puede calcular el peso
específico natural del suelo (γn) mediante la expresión 7.2:
γn =
Wt
Vt
(7.2)
cuyo valor es generalmente aproximado a 2. La expresión anterior indica que este
parámetro define la relación entre el peso total del suelo (sólido + agua) y el volumen
total que ocupa el mismo.
El peso específico seco del suelo (γd) puede calcularse gracias a que el
volumen de suelo es conocido. Así:
γd =
Ws
Vt
(7.3)
La expresión 7.3 define la relación entre el peso del sólido que compone la
muestra de suelo ensayada y el volumen total que ocupa la misma.
99
VII - Resultados experimentales e interpretación
Se calculan seguidamente dos parámetros muy importantes en la definición
del suelo, que son la porosidad (n) y el índice de poros (e).
Se puede definir porosidad (7.4) como la fracción de volumen ocupada por
los poros, tanto si éstos están llenos de agua como si lo están de aire o de una mezcla de
ambos.
n=
Vp
(7.4)
Vt
Se define el índice de poros (7.5) como la razón del espacio ocupado por los
poros al espacio ocupado por las partículas sólidas.
e=
Vp
(7.5)
Vs
Conocidos todos estos parámetros se calcula el grado de saturación (Sr) de
las muestras (7.6) que se define como la fracción del volumen total de los poros que está
ocupada por agua.
sr =
Vω
Vp
(7.6)
Estos parámetros definidos se han calculado tanto para la fase inicial, que se
refiere antes de iniciar el ensayo, como para la fase final, referida ésta una vez ha
finalizado el ensayo, considerando en este caso el grado de saturación igual a uno, por
tanto Vw=Vp, para la realización de todos los cálculos.
En el caso de las muestras con las que no se han hecho probetas no se
conoce el volumen de suelo ensayado, de manera que sólo se puede calcular la
humedad.
En la tabla 7.2 se muestran los valores obtenidos de cada uno de parámetros
definidos como las propiedades básicas del suelo para cada una de las muestras
ensayadas.
100
PROPIEDADES BÁSICAS DEL SUELO
M1a
DESCRIPCIÓN MATERIAL
w nat INI (%)
M1b
M2a
M2a1ª
M2a2ª
M2a3ª
M2a4ª
Arcilla roja con
Arcilla roja con
Arcilla roja con
abundantes nódulos abundantes nódulos
ocasionales nódulos de
de pizarra de
de pizarra de
pequeño tamaño de
tamaño mediano a tamaño mediano a
pizarra
grande
grande
12.40
12.14
M3a
M3b
M3c
Arcilla roja con
Arcilla roja con
Arcilla roja con
abundantes
abundantes
abundantes
nódulos de
nódulos de
nódulos de
pizarra de
pizarra de
pizarra de
tamaño pequeño tamaño pequeño tamaño pequeño
a grande
a grande
a grande
13.19
12.51
12.29
M3c1ª
M3c2ª
M3c3ª
M3d
Arcilla roja con
abundantes
nódulos de
pizarra de
tamaño pequeño
a grande
11.31
14.00
13.41
12.97
10.95
13.17
14.20
13.56
w nat FIN (%)
19.10
19.34
18.59
12.32
16.63
17.98
12.85
γ n INI
(g/cm3)
1.96
1.95
1.96
2.01
1.94
1.86
1.90
γ n FIN
(g/cm3)
2.10
2.09
2.11
2.24
2.15
2.12
2.23
γ d INI
(g/cm3)
1.76
1.72
1.74
1.81
1.72
1.62
1.67
γ d FIN
(g/cm3)
1.76
1.75
1.78
2.00
1.84
1.79
1.98
0.54
0.54
0.53
0.46
0.54
0.63
0.59
e
INI
e
FIN
0.51
0.51
0.49
0.33
0.44
0.48
0.34
n
INI
(%)
33.07
35.05
34.47
31.58
35.19
38.68
37.02
n
FIN
(%)
33.61
33.88
33.01
24.61
30.59
32.27
25.41
S r INI
0.69
0.66
0.65
0.63
0.64
0.60
0.61
S r FIN
1.00
1.00
1.00
1.00
1.00
1.00
1.00
wL
49.00
48.50
33.70
39.50
35.00
37.85
30.50
wP
22.48
24.11
17.99
22.20
20.16
18.84
17.78
IP
26.52
24.39
15.71
17.30
14.84
19.01
12.72
CL
CL
CL
CL
CL
CL
CL
CLASIFICACIÓN CASAGRANDE
Tabla 7.2: Propiedades básicas del suelo para cada una de las muestras ensayadas.
VII - Resultados experimentales e interpretación
7.5 Resultados obtenidos a partir del triaxial.
A continuación se presentan los resultados experimentales obtenidos tras la
realización del ensayo triaxial convencional; se exponen básicamente en forma de tablas
y gráficos donde se presentan relacionando comportamientos bajo idénticas condiciones
de trabajo. En el apartado 7.6 (dedicado a la interpretación de los resultados) se discuten
los resultados aquí presentados. En el anejo 2 hay una recopilación de las hojas de
laboratorio rellenadas durante la realización de los diferentes ensayos, de manera que
los resultados numéricos, en los cuales se basan las conclusiones, quedan ilustrados en
este trabajo.
El ensayo triaxial, como se explica en el apartado 5.5, aplica sobre el
contorno de la muestra tensiones normales con el objetivo de determinar las propiedades
esfuerzo-deformación del suelo.
De la primera etapa, llamada saturación, no se guardan datos en el PC pero
se anotan manualmente cada diez segundos para seguir su tendencia. Estos valores,
descritos en el apartado 5.5.4.b, sirven como comprobación de la saturación de la
muestra previo al inicio del ensayo.
Seguidamente la muestra se consolida isotrópicamente con drenaje antes de
llegar a la fase de aplicación del desviador y la consiguiente rotura de la misma. En esta
fase de consolidación se ha calculado el volumen de la muestra en cada instante frente a
las tensiones efectivas expresadas en el espacio de Cambridge (p’). Todos estos valores
se almacenan en el PC.
Para la representación de los resultados es más interesante expresar cómo
varía el índice de poros en lugar de la variación del volumen respecto a las tensiones
efectivas. Para conocer esta variación de índice de poros se sigue el procedimiento en
orden inverso al utilizado en el ensayo, es decir, se comienza calculando el índice de
poros final con la relación (7.7) y a partir de éste, mediante el incremento de índice de
poros (7.8) que se obtiene utilizando la expresión (7.9), se van obteniendo los índices de
poros intermedios hasta llegar al inicial que puede comprobarse mediante (7.10).
ef =
γs
×ω f
γω
(7.7)
∆e
1+ ef
(7.8)
ε vol = −
∆V
VT
(7.9)
γs
× ωi
γω
(7.10)
ε vol =
ei =
102
VII - Resultados experimentales e interpretación
donde:
ef: índice de poros final.
γs: peso específico de las partículas sólidas.
γw: peso específico del agua.
wf: humedad final de la probeta.
εvol: deformación volumétrica
e: incremento del índice de poros.
V: incremento de volumen en la probeta.
VT: volumen total de la probeta en su estado inicial.
ei: índice de poros inicial.
wi: humedad inicial de la probeta.
Finalmente, una vez terminada la consolidación, se procede a realizar la
rotura de la muestra, de forma no drenada, aumentado el esfuerzo axial mientras se
mantiene constante el confinamiento lateral. Todos los ensayos realizados para las
diferentes muestras de suelo se les somete a una tensión desviadora de compresión.
Esta fase de rotura se realiza a deformación controlada, el pistón se desplaza
a una velocidad determinada respecto a la célula, y se mide la tensión desviadora.
Igual que en la fase de consolidación, los valores medidos cada instante de
tiempo se almacenan en el PC. A partir de estos datos se pueden calcular gran cantidad
de parámetros. Se han calculado los valores de las tensiones expresadas en el plano de
Cambridge mediante q, p y p’ (7.11) y a partir de éstos se han representado las
trayectorias de tensiones totales y efectivas (figuras 7.6 a 7.9 ) para cada muestra.
q = σ1 − σ 3
p=
p′ =
donde:
σ 1 + 2σ 3
(7.11)
3
σ 1′ + 2σ 3′
3
1:
es la tensión principal mayor
:
3 es la tensión principal menor
En las figuras 7.11 y 7.12 se muestran las trayectorias de tensiones para
cada muestra, M2a y M3c respectivamente, de la que se obtiene la recta de rotura y a
partir de ésta el valor de M que se define como la pendiente de la misma. De M se
obtiene el valor del ángulo de rozamiento interno de las partículas definido como que
se calcula mediante la expresión 7.12, considerando el valor de la cohesión c’ como
nulo.
M = 6 * sen
/ ( 3 – sen
103
)
(7.12)
VII - Resultados experimentales e interpretación
El valor de M obtenido para la muestra M2a es de 0,88 y a partir de la
expresión 7.12 se obtiene el valor de =22,75º. Así mismo, para la muestra M3c el
valor de M obtenido es de 0,875 y el valor del ángulo de rozamiento interno es de
=22,45º.
También se ha calculado la deformación vertical producida en la muestra en
cada instante (7.13) y se ha representado frente al desviador calculado en (7.11).
(figuras 7.12 a 7.16).
ez =
h0 − h1
h0
(7.13)
donde:
ho: altura inicial de la probeta (mm).
hi: altura de la probeta en cada instante (mm).
ez: deformación vertical en tanto por uno.
La rotura se produce de forma no drenada de modo que existe un
incremento en la presión de agua en el interior de la muestra. Esta presión de agua se
mide directamente en el aparato triaxial en cada instante de tiempo, de modo que el
incremento es inmediato tomando como referencia la presión de agua en el instante de
tiempo igual a cero. En las figuras 7.12 a 7.16 se representa el incremento de la presión
de agua frente a la deformación vertical para cada una de las muestras ensayadas.
Finalmente se ha calculado el valor del parámetro Cc obtenido a partir de la
correlación con el parámetro que se define como la pendiente de la recta formada en el
plano e - p’ en escala semilogarítmica. Este valor de Cc se ha obtenido de la correlación
hecha mediante la relación 7.14.
Cc = ln 10 = 2,303
(7.14)
En la tabla 7.3 se muestran los valores de Cc obtenidos para cada una de las
muestras ensayadas.
λ
Cc
M2a1ª
0.008
0.019
M2a2ª
0.011
0.026
M2a3ª
0.023
0.053
M3c1ª
0.03
0.069
M3c2ª
0.032
0.074
Tabla 7.3: Valores de Cc obtenidos a partir de .
A continuación se presentan los resultados en forma gráfica para las
diferentes probetas ensayadas (figuras 7.6 a 7.16). El eje de abscisas se representa en
algunos de los casos en escala logarítmica, de manera que los puntos están mejor
distribuidos y pueden así estudiarse con mayor claridad la distribución de los mismos.
siguientes:
Las unidades en que se expresan los valores de las gráficas son las
104
VII - Resultados experimentales e interpretación
•
•
•
•
•
Desviador, q: kPa
p: kPa
Índice de poros, e: adimensional
Deformación vertical, ez: tanto por uno
Presión de poros, u: kPa
7.5.1 Trayectorias de tensiones totales y efectivas.
En primer lugar se muestran las gráficas donde se representan las
trayectorias de tensiones totales y efectivas para cada muestra por separado (figuras 7.6
a 7.9) y una gráfica que reúne las trayectorias de tensiones de las diferentes probetas que
corresponden a la misma muestra (figuras 7.11 y 7.12).
Trayectorias de tensiones // M2a1ª - Pau1
400
300
p
200
p'
10 0
0
0
10 0
200
300
p ,p ' ( k P a )
400
50 0
600
Figura 7.6: Trayectorias de tensiones totales y efectivas - muestra M2a1ª
Trayectoria de tensiones // M2a2ª - Pau3
800
600
Efect ivas
400
To t ales
200
0
0
200
400
600
800
10 0 0
p , p' (kP a )
Figura 7.7: Trayectorias de tensiones totales y efectivas - muestra M2a2ª
105
12 0 0
VII - Resultados experimentales e interpretación
Trayectorias de tensiones // M2a3ª - Pau 2
800
600
Tot a le s
400
Ef e c t iva s
200
0
0
200
400
600
800
1000
1200
p , p ' ( kP a )
Figura 7.8: Trayectorias de tensiones totales y efectivas - muestra M2a3ª
q - p,p' - Rotura no drenada // Pau4r
300
250
200
q -p
150
q -p '
100
50
0
0
200
400
600
800
1000
1200
p , p ' ( kP a )
Figura 7.9: Trayectorias de tensiones totales y efectivas - muestra M3c1ª
q-p,p' - Consol idación no drenada // Pau5
300
250
200
q-p'
150
q-p
100
50
0
0
100
200
300
400
500
p,p' ( kP a )
600
700
800
Figura 7.10: Trayectorias de tensiones totales y efectivas - muestra M3c2ª
106
900
VII - Resultados experimentales e interpretación
Recta de rotura // M2a
1000
950
900
850
800
750
700
650
P au1/ E f ec t i v as
P au1/ T ot al es
q (kPa)
600
P au2/ E f ec t i v as
550
P au2/ T ot al es
500
P au3/ E f ec t i v as
450
P au3/ T ot al es
400
350
300
250
200
150
100
50
0
0
50
100
150
200
250
300
350
400
450
500
550
600
650
700
750
800
850
900
950
1000
p,p' (kPa)
Figura 7.11: Trayectorias de tensiones totales y efectivas - muestra M2a
Recta de rotura // M3c
750
70 0
6 50
600
550
50 0
4 50
Pau4/Efectivas
400
Pau4/T otales
3 50
Pau5/Efectivas
300
Pau5/T otales
2 50
200
150
10 0
50
0
0
50
10 0
150
200
2 50
300
3 50
400
4 50
50 0
550
600
6 50
70 0
p,p' (kP a )
Figura 7.12: Trayectorias de tensiones totales y efectivas - muestra M3c
107
750
800
8 50
900
9 50
10 0 0
7.5.2 Diagramas de los resultados obtenidos.
q - ez // M2a1ª - Pau1
q - p' // M2a1ª - Pau1
250
250
200
200
150
150
100
100
50
50
0
0
0
50
100
150
200
250
300
350
400
0
0,05
p ' ( kP a )
0,1
0,15
0,2
0,25
0,2
0,25
e z ( t a nt o p o r uno )
e - ln p' // M2a1ª - Pau1
inc u - ez // M2a1ª - Pau1
0,39
70
0,389
60
0,388
50
0,387
0,386
40
0,385
30
0,384
u o=284,859
20
0,383
10
0,382
0
0,381
2,7183
7,38905
ln p ' ( kP a )
Figura 7.13: Diagramas de resultados para la muestra M2a1ª
0
0,05
0,1
0,15
e z ( t a nt o p o r uno )
q - p' // M2a2ª - Pau3
q - ez // M2a2ª - Pau3
350
300
300
2 50
250
200
200
150
150
10 0
100
50
50
0
0
0
50
100
150
200
250
300
350
0
0 ,0 5
p' (kP a )
0 ,1
0 ,15
0 ,2
0 ,2 5
0 ,2
0 ,2 5
e z (ta nto po r uno )
e - ln p' // M2a2ª - Pau3
inc u - ez // M2a2ª - Pau3
0 ,4 3
2 50
0 ,4 2
200
0 ,4 1
150
0 ,4
10 0
0 ,3 9
50
0 ,3 8
2 ,718 3
0
7,3 8 9
ln p' (kP a )
Figura 7.14: Diagramas de resultados para la muestra M2a2ª.
0
0 ,0 5
0 ,1
0 ,15
e z (ta nto po r uno )
q - p' // M2a3ª - Pau2
q - ez // M2a3ª - Pau2
350
350
300
300
250
250
200
200
150
150
100
100
50
50
0
0
0
50
100
150
200
250
300
350
400
4 50
500
550
0
600
0,05
0,1
0,15
0,2
0,25
e z (tanto po r uno )
p' (kP a)
e - ln p' // M2a3ª - Pau2
inc u - ez // M2a3ª - Pau2
0,41
350
0,405
300
u o = 502,592 kP a
0,4
250
0,395
200
0,39
150
0,385
100
0,38
50
0,375
0
0,37
2,7183
7,389
ln p' (kP a )
Figura 7.15: Diagramas de resultados para la muestra M2a3ª.
0
0,05
0,1
0,15
e z ( ta nt o po r uno )
0 ,2
0,2 5
q-p' - Rotura no drenada // Pau4r
q-ez - Rotura no drenada // Pau4r
30 0
30 0
2 50
250
20 0
20 0
150
150
10 0
10 0
50
50
0
0
0
50
100
150
200
2 50
300
350
40 0
0
450
0 ,05
0,1
0,15
0 ,2
e z (ta nto po r uno )
p' (kP a )
e - ln p' // M3c1ª - Pau4
inc u-ez - Rotura no drenada // Pau4r
3 50
0,39
300
0,38
2 50
0,37
200
0,36
150
0,35
10 0
0,34
50
0
0,33
2,7183
7,389
ln p' (kP a)
Figura 7.16: Diagramas de resultados para la muestra M3c1ª.
0
0 ,0 5
0 ,1
e z ( t a nt o po r uno )
0 ,15
0 ,2
q-p' - Rotura no drenada // Pau5
q-ez - Rotura no drenada // Pau5
30 0
300
250
250
20 0
200
150
150
10 0
100
50
50
0
0
0
50
10 0
150
200
250
3 00
0
350
0,05
0,1
0,15
0,2
0,25
0,2
0 ,2 5
e z (ta nto po r uno )
p' (kP a )
e - ln p' // M3c2ª - Pau5
inc u-ez - Rotura no drenada // Pau5
0,405
250
0,4
0,395
200
0 ,3 9
0,385
150
0 ,3 8
0,375
100
0,37
0,365
50
0 ,3 6
0,355
2,7183
7,389
ln p' (kP a )
Figura 7.17: Diagramas de resultados para la muestra M3c2ª.
0
0
0,05
0,1
0,15
e z (ta nto po r uno )
VII - Resultados experimentales e interpretación
7.6 Interpretación de los resultados obtenidos en el ensayo triaxial.
En este ensayo (figuras 7.6 a 7.17) el comportamiento del suelo sigue
bastante bien la predicción del Modelo de Cam-Clay (apartado 5.5.5), teniendo en
cuenta que las muestras ensayadas en el laboratorio no se pueden considerar totalmente
inalteradas. Las predicciones más fiables que realiza este modelo es en el análisis del
comportamiento de arcillas, que es el caso que nos ocupa.
Observando los resultados obtenidos para las probetas pertenecientes a la
muestra M2a podemos hacer una diferenciación entre la trayectoria de tensiones
efectivas para la probeta M2a1ª y las trayectorias de estas tensiones para las probetas
M2a2ª y M2a3ª. Así podemos decir que se trata de una trayectoria de tensiones efectivas
elásticas la perteneciente a la primera probeta y de unas trayectorias de tensiones
efectivas elasto-plásticas las pertenecientes a las dos últimas.
En el apartado 5.5.5.4 se definió la superficie de fluencia como aquella que
separa, en el plano de tensiones, los estados tensionales que producen deformaciones
elásticas de los que provocan respuestas plásticas. Se observa en la figura 7.11 cómo la
tensión efectiva perteneciente a la probeta M2a1ª permanece constante hasta un punto
máximo en el que alcanza la fluencia y entonces aparece la trayectoria de tensiones
efectivas elasto-plástica. Este valor constante de la tensión efectiva se debe a que la
trayectoria evoluciona en el interior de la superficie de fluencia con lo que no existe la
posibilidad de deformación volumétrica plástica y para satisfacer la ecuación 5.33 la
deformación elástica también es nula.
Finalmente, esta trayectoria de tensiones efectivas perteneciente a la probeta
M2a1ª corresponde a un ensayo triaxial no drenado fuertemente sobreconsolidado.
La trayectoria de tensiones de la muestra M2a2ª (figura 7.11) transcurre un
tramo por el interior de la superficie de fluencia con la tensión efectiva constante y a
partir del desviador de 70 kPa aproximadamente aparecen las deformaciones plásticas.
Según se explica en el apartado 5.5.5.7.c., este punto donde se interceptan la trayectoria
y la superficie de fluencia da lugar a un incremento del vector de deformación plástica
dirigido hacia la derecha, lo que implica una compresión volumétrica plástica. El suelo
tiende a rigidizarse plásticamente, y la actual superficie de fluencia se incrementa en
tamaño.
La trayectoria de tensiones de la muestra M2a3ª corresponde a un
incremento de deformación que ocurre en el punto más alto de la superficie de fluencia.
La fluencia, en este caso, tiene lugar con un incremento del vector plástico con
dirección paralela al eje del desviador, lo que implica deformación plástica nula. La
deformación continúa indefinidamente sin cambio en el tamaño de la superficie de
fluencia. En la figura 5.29 puede seguirse con mayor claridad el proceso explicado en
este último párrafo.
Las probetas pertenecientes a la muestra M3c presentan unos resultados
muy similares a los explicados para la muestra M2a. Se ensayaron estas muestras
intentando aplicar las condiciones iniciales en las que se encontraban y se sometieron a
113
VII - Resultados experimentales e interpretación
unas tensiones semejantes a las aplicadas en las de la muestra M2a para poder así
comparar los resultados.
Únicamente cabe diferenciar que la muestra M3c presenta una mayor
resistencia frente a la aplicación de las cargas que la muestra M2a. Se observa en la
figura 7.12 que la deformación plástica aparece en las probetas M3c a partir de 230 kPa
en el desviador, en cambio las probetas M2a a partir de la aplicación de un desviador de
190 kPa ya se produce la rotura. Esto puede explicarse debido a la diferente
granulometría, presentando la muestra M3c una mayor proporción de partículas gruesas
que las presentes en la muestra M2a, lo que ayuda a ganar resistencia al conjunto frente
a las cargas aplicadas.
A continuación, en las figuras 7.13 a 7.17, se presentan los gráficos con los
resultados obtenidos en cada una de las muestras ensayadas.
La probeta M2a1ª ha sido sometida a unas condiciones iniciales muy
sobreconsolidadas como se representa en la figura 7.13. La primera fase de carga es
puramente elástica sin cambios en la tensión efectiva principal hasta que la superficie de
fluencia es alcanzada (punto más alto de la trayectoria). La deformación de corte es
puramente elástica, como se presenta en la gráfica superior derecha de la misma figura.
Se puede observar que la presión de poros es igual a los cambios de la tensión principal
total. Esta presión se reduce respecto a su máximo valor y podría resultar negativa.
Las probetas M2a2ª y M3c2ª se han sometido a condiciones ligeramente
sobreconsolidadas. Se representa en las figuras 7.14 y 7.17 exceptuando en que
inicialmente existe un fase elástica en la que la tensión efectiva permanece constante
hasta que la tensión alcanza el valor de la fluencia. De estas gráficas se puede deducir:
- el ensayo está restringido a seguir una deformación constante en el plano
de compresión.
- las deformaciones plásticas sólo pueden ocurrir si la tensión efectiva
permanece en la actual superficie de fluencia.
Se puede resumir diciendo que se mantienen los valores iniciales de p’ hasta
que el valor del desviador q es lo suficientemente grande como para dar el estado de
tensiones correspondiente a la superficie de fluencia y permitir que las deformaciones
plásticas ocurran.
El estado elástico se asocia únicamente a las deformaciones de corte y a los
cambios de presión intersticial, como puede verse en las gráficas superior e inferior
derecha de las figuras 7.14 y 7.17. Cuando la fluencia comienza aparecen
deformaciones de corte plásticas y hay una inflexión en las curvas como se muestra en
las figuras que presentan las trayectorias de tensiones efectivas. Cuando empieza la
fluencia, estas trayectorias tienden a ir hacia la izquierda y existe una relación con la
presión de poros.
Finalmente, las probetas M2a3ª y M3c1ª se han sometido a condiciones
normalmente consolidadas como se muestra en las figuras 7.15 y 7.16. Las trayectorias
114
VII - Resultados experimentales e interpretación
de tensiones efectivas en este caso empiezan directamente en el punto de intersección de
la superficie de fluencia con el eje horizontal, de modo que se produce plasticidad desde
el mismo momento en el que empieza la fase de rotura en el ensayo. Todo lo dicho en
los párrafos anteriores es adaptable a este caso de forma análoga.
115
φ (º)
Μ
Ensayo triaxial
M2a
0.880
λ
M2a1ª
M2a2ª
M2a3ª
M3c
0.875
M3c1ª
M3c2ª
Tabla 7.4: Propiedades geotécnias obtenidas del ensayo triaxial convencional.
qrotura (kPa)
190
Cc
22.75
0.008
0.011
0.023
0.019
0.026
0.053
0.030
0.032
0.069
0.074
22.45
G (MPa)
6.06
34.19
5.67
230
5.68
6.90
VII - Resultados experimentales e interpretación
7.7 Resultados obtenidos del ensayo triaxial de columna resonante.
A continuación se presentan, en forma de tablas y gráficos, los resultados
experimentales obtenidos en el ensayo triaxial de columna resonante. Estos resultados
se discutirán en el apartado 7.8, dedicado a la interpretación de los resultados.
De la muestra M2a se tallan cuatro probetas, de las cuales tres de ellas se
ensayan en el aparato triaxial convencional obteniéndose los resultados expuestos en el
apartado 7.5, y la cuarta se ensaya en el aparato triaxial de columna resonante.
De la muestra M3c se realizan tres probetas, ensayándose dos de ellas en el
aparato triaxial convencional y la tercera en el de columna resonante.
Las figuras que se presentan en este apartado muestran el módulo de corte
(G) frente a la deformación angular ( ) representada en escala logarítmica para que así
los puntos se encuentren mejor distribuidos.
Para correlacionar los resultados obtenidos en el ensayo triaxial
convencional con los obtenidos a partir del ensayo triaxial de columna resonante las
presiones de confinamiento que se han utilizado en este último han sido las tensiones de
confinamiento con las que se ha llegado a la rotura en el triaxial para cada una de las
probetas ensayadas.
Es importante destacar que al ser el ensayo triaxial de columna resonante no
destructivo, en una sola probeta ensayada se ha podido aplicar las diferentes tensiones
que se aplicaron a cada una de las probetas ensayadas en el triaxial convencional.
A continuación se exponen en forma de gráficos los resultados obtenidos
para cada una de las presiones de confinamiento y finalmente se contemplan los
resultados obtenidos para cada presión juntos en una misma gráfica.
Puede observarse que para cada presión se ha obtenido un conjunto de
puntos que siguen una ley bastante lineal. En el anejo 2 se muestran los resultados
numéricos en forma de tabla.
Las unidades en que se encuentran expresados los valores de las gráficas
son las siguientes:
•
•
•
Módulo de corte, G: Mpa
Desplazamiento: % en deformación angular
Presión de confinamiento, σ: κPa
Hay que tener en cuenta que las probetas se colocaron directamente en el
equipo, y en general no estaban totalmente saturadas.
117
VII - Resultados experimentales e interpretación
7.7.1 Resultados de la probeta M2a4ª.
G - l og def ormaci ón angul ar
M2a4ª / 130 kPa
250
200
G (MPa)
150
100
50
0
1. 00E- 04
1. 00E- 03
Def or maci ón angul ar ( %)
1. 00E- 02
1. 00E- 01
Figura 7.18: Gráfica módulo de corte versus deformación angular para la probeta M2a4ª a una presión de
confinamiento de 130 kPa.
118
VII - Resultados experimentales e interpretación
G - l og def ormaci ón angul ar
M2a4ª / 300 kPa
250
200
G (MPa)
150
100
50
0
1. 00E- 04
1. 00E- 03
Def or maci ón angul ar ( %)
1. 00E- 02
1. 00E- 01
Figura 7.19: Gráfica módulo de corte versus deformación angular para la probeta M2a4ª a una presión de
confinamiento de 300 kPa.
G - l og def ormaci ón angul ar
M2a4ª / 400 kPa
300
250
G (MPa)
200
150
100
50
0
1. 00E- 04
1. 00E- 03
1. 00E- 02
Log def or maci ón angul ar ( %)
1. 00E- 01
Figura 7.20: Gráfica módulo de corte versus deformación angular para la probeta M2a4ª a una presión de
confinamiento de 400 kPa.
119
VII - Resultados experimentales e interpretación
M2a4ª.
300
Se expone a continuación el conjunto de resultados para la probeta ensayada
G - l og def ormaci ón angul ar
M2a4ª
250
G (MPa)
200
130 kPa
150
300 kPa
400 kPa
100
50
0
1. 00E- 04
1. 00E- 03
1. 00E- 02
Log def or mac i ón angul ar ( %)
Figura 7.21: Curvas del módulo de corte versus la deformación angular para la probeta M2a4ª.
120
1. 00E- 01
VII - Resultados experimentales e interpretación
7.7.2 Resultados de la probeta M3c3ª.
G - log deformación angular
M 3c3ª / 300 kPa
250
200
150
100
50
0
1,00E- 04
1,00E- 03
Lo g D e f o rma c i ó n a ng ula r ( %)
1,00E-02
1,00E- 01
Figura 7.22: Gráfica módulo de corte versus deformación angular para la probeta M3c3ª a una presión de
confinamiento de 300 kPa.
G - l og def ormaci ón angul ar
M3c3ª / 400 kPa
250
200
G (MPa)
150
100
50
0
1. 00E- 04
1. 00E- 03
1. 00E- 02
Log def or mac i ón angul ar ( %)
1. 00E- 01
1. 00E+00
Figura 7.23: Gráfica módulo de corte versus deformación angular para la probeta M3c3ª a una presión de
confinamiento de 400 kPa.
121
VII - Resultados experimentales e interpretación
M3c3ª.
Se expone a continuación el conjunto de resultados para la probeta ensayada
G - l og def ormaci ón angul ar
M3cª
250
200
150
G (MPa)
300 kPa
400 kPa
100
50
0
1. 00E- 04
1. 00E- 03
Log def or mac i ón angul ar ( %)
1. 00E- 02
1. 00E- 01
Figura 7.24: Curvas del módulo de corte versus la deformación angular para la probeta M3c3ª.
7.7.3 Comparación con los resultados obtenidos en el triaxial.
Una vez obtenidos los valores de los módulos de corte tanto para la probeta
de la muestra M2a como para la probeta de la muestra M3c se pueden comparar con los
resultados obtenidos en el ensayo triaxial convencional.
Las comparaciones se realizan con el módulo de corte elástico en el ensayo
triaxial obtenido de la parte inicial de la gráfica q-ez, considerada como la parte elástica.
Este módulo de corte elástico se obtiene mediante la relación 7.15:
dq
= dε q
3G
(7.15)
donde:
q: desviador en kPa.
q: deformación de corte (en el caso no drenado coincide con 1).
G: módulo de corte elástico (obtenido de probetas ensayadas en el
triaxial; saturadas).
En la tabla 7.5 se recopilan los valores del módulo de corte elástico en el
ensayo triaxial para las muestras ensayadas.
122
VII - Resultados experimentales e interpretación
CÁLCULO DEL MÓDULO DE CORTE (G) ELÁSTICO EN EL ENSAYO TRIAXIAL CONVENCIONAL PARA LAS MUESTRAS
M2a Y M3c.
MUESTRA
REF.
TENSIÓN
INICIAL
q1
qo
∆q
(ez)1
(ez)o
∆ez
G
kPa
KPa
kPa
kPa
tanto por
uno
tanto por
uno
tanto por
uno
MPa
M2a3ª
PAU2
400
47,49
1,76
45,72
2,69E-03
0,00
2,69E-03
5,67
M2a2ª
PAU3
300
89,87
29,97
59,89
0,77E-03
1,88E-04
5,84E-04
34,19
M2a1ª
PAU1
130
46,05
2,27
43,78
2,41E-03
0,00
2,41E-03
6,06
M3c1ª
PAU4
400
47,13
17,61
29,53
13,12E-03
1,14E-02
1,73E-03
5,68
M3c2ª
PAU5
300
50,76
10,73
40,02
27,12E-03
2,52E-02
1,93E-03
6,90
Tabla 7.5: Valores de G elástico, para la probeta M2a4ª, calculados a partir del ensayo triaxial convencional.
En las figuras 7.25 y 7.26 se muestran los resultados obtenidos, para las
muestras M2a2ª y M3c3ª, mediante los dos tipos de ensayos y se correlacionan en una
gráfica distinta para cada una de las muestras.
Estos valores del módulo de corte se pueden comparar con los obtenidos a
partir de los resultados de la campaña de prospección sísmica realizada por el Servicio
de Geofísica Aplicada de la Universidad Politécnica de Cataluña (Clapés, 2000). El
valor del módulo de corte obtenido en el apartado 4.5 es de 7.500 Mpa, valor muy
elevado respecto a los obtenidos mediante el ensayo triaxial de columna resonante. Esto
se interpreta suponiendo que este valor tan elevado del módulo de corte corresponde a
las pizarras situadas debajo de las arcillas del cuaternario y por tanto, pertenecientes a
terrenos diferentes.
123
VII - Resultados experimentales e interpretación
G - Log deformación angular // M2a
300
250
G (MPa)
200
M 2 a 13 0 kPa
150
TRIAXIAL 13 0 kPa
M 2 a 3 0 0 kPa
TRIAXIAL 3 0 0 kPa
100
M 2 a 4 0 0 kPa
TRIAXIAL 4 0 0 kPa
50
0
1,00E-04
1,00E-03
1,00E-02
Log deformación angular (%)
1,00E-01
1,00E+00
Figura 7.25: Correlación entre los valores del módulo de corte obtenido en el ensayo de columna resonante con los
valores del módulo de corte elástico obtenido a partir del ensayo triaxial convencional para la muestra M2a.
Puede observarse una diferencia sustancial entre el resultado obtenido para
el ensayo triaxial de columna resonante y el obtenido para el ensayo triaxial
convencional. Esta diferencia entre ambos se debe a que el ensayo triaxial convencional
se realiza tras saturar las probetas mientras que las probetas ensayadas en el aparato de
columna resonante no lo están.
124
VII - Resultados experimentales e interpretación
G - Log deformación angular // M3c
250
200
G (MPa)
150
M 3 c 3 0 0 kPa
TRIAXIAL 3 0 0 kPa
100
M 3 c 4 0 0 kPa
TRIAXIAL 4 0 0 kPa
50
0
1,00E-04
1,00E-03
1,00E-02
Log deformación angular (%)
1,00E-01
1,00E+00
Figura 7.26: Correlación entre los valores del módulo de corte obtenido en el ensayo de columna resonante con los
valores del módulo de corte elástico obtenido a partir del ensayo triaxial convencional para la muestra M3c.
Es válido el comentario realizado para la gráfica anterior referente a la
saturación de las probetas ensayadas en los equipos de columna resonante y triaxial.
125
VII - Resultados experimentales e interpretación
7.8 Interpretración de los resultados del ensayo triaxial de columna
resonante.
El parámetro del módulo de corte informa de la rigidez del suelo. Según las
figuras 7.21 y 7.24 el valor de este parámetro en la probeta M2a4ª es superior al
obtenido para la probeta M3c3ª, lo que supone que la primera tiene mayor rigidez que la
segunda. Este comportamiento se puede atribuir a la diferente granulometría que
presentan las probetas (figura 7.4) lo que provoca una diferente estructura en las
mismas. La muestra M2 tiene un porcentaje mayor de partículas finas que la muestra
M3, esto favorece una mayor compacidad de la estructura dado que estas partículas
arcillosas de menor tamaño rellenan más fácilmente las cavidades entre las mismas.
Hay que comentar que los valores de la presión de confinamiento a los que
se han sometido las probetas, corresponden a las presiones de cámara durante la fase de
rotura en el ensayo triaxial, de este modo se procede a la correlación de los datos
obtenidos en los diferentes ensayos (figuras 7.25 y 7.26).
Los valores obtenidos del módulo de corte son mucho menores en el triaxial
en comparación con los resultantes de la columna resonante. Se observa así como en el
ensayo triaxial, donde las probetas se llevan a rotura y se someten a un rango mayor de
deformaciones, presentan una resistencia al corte muy inferior. Es importante hacer
saber que las probetas estaban no saturadas en el aparato triaxial de columna resonante,
y por tanto el valor del módulo de corte puede ser condicionalmente mayor por este
efecto.
Otros aspectos a tener en cuenta son que debido al periodo de tiempo que se
ha tenido consolidando la probeta puede deformarse y la utilización de aire como
presión de cámara puede hacer bajar el grado de saturación de la muestra a causa de que
la membrana de látex no es del todo impermeable al aire. Esto no se ha estudiado a
fondo al no ser el objetivo de este trabajo.
7.9 Parámetros geotécnicos obtenidos del ensayo de columna resonante
Ensayo columna resonante
G (MPa)
300 kPa
130 kPa
M2a4ª
100
225
M3c3ª
190
Tabla 7.6: Parámetros geotécnicos obtenidos del ensayo triaxial de columna resonante
126
400 kPa
250
230