0.1. Aplicaciones de las integrales definidas

UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
MATEMATICAS II
MAT- 022
Ejercicios
0.1.
Aplicaciones de las integrales definidas
Cálculo de volúmenes por secciones transversales y por rotación alrededor de un eje Cálculo de
volúmenes por medio de casquillos cilı́ndricos Longitudes de curvas planas. Momentos y centro de masa
Áreas de superficies de revolución y el teorema de Pappus Trabajo. Presiones y fuerzas en fluidos
1. Sea R la región en el semiplano {(x, y) ∈ R2 | x ≥ 0}, limitada por las curvas y = ex , y = cos x y la
recta x = 2π.
a) Calcular el área de la región R.
b) Escriba la integral que determina el volumen del sólido generado po R al rotar en torno:
i) al eje y.
ii) a la recta y = −1.
2. La superficie encerrada por x = y 2 ; x = 8 − y 2 , gira en torno de x = −1. Encuentre el volumen del
sólido ası́ formado.
3. Calcular la longitud de la curva:
x = a cos t + at sin t
;
y = a sin t − at cos t
0 ≤ t ≤ π/2; a > 0
4. Comprobar que un arco de la curva y = sin x, x ∈ [0, 2π] tiene la misma longitud que la elipse:
1
x2 + y 2 = 1
2
5. Calcule la longitud del arco de la curva:
x
Z
y=
p
t2 − 1dt,
1
entre los puntos para los cuales x = 1, x = 2.
6. Considere las curvas:
y = sin x
2
x2 + yb2 = 1
1
;
;
0≤x≤π
y≥0
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
a) Detremine b ∈ R+ tal que las longitudes de ambas curvas sean las mismas.
Indicación: Las integrales son del tipo ”Integrales elı́pticas” y no son calculables vı́a antiderivadas.
b) Compare las áreas de las superficies de revolución generadas por las curvas anteriores(Cuando
ambas tienen igual longitud) al girar en torno al eje X.
7. Determine la longitud del arco de la curva:
x(t)
y(t)
√
= ln 1 + t2
= arctan(t)
Desde t = 0 a t = 1.
8. La base de cierto sólido es una región del plano xy acotada por las gráficas de y = x2 ; y = x3 . Determine
el volumen de este sólido si cada sección transversal perpendicular al eje x es un cuadrado cuya base
está en el plano xy.
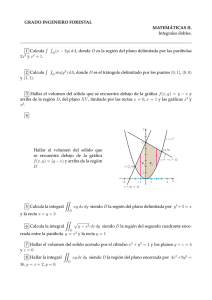
9. Sea R la región encerrada por la gráfica de la función f (θ) = sin θ comprendida entre θ = −π, θ = π e
y = 0. Exprese las integrales que permiten cañcular el volumen del sólido S de revolución generado al
rotar la región R en torno a la recta θ = 0.
10. Sea R la región bajo la curva y =
√
1
,
x(1+x)
con x ∈ [1. + ∞[.
a) Obtenga una integral impropia para el área de R mediante la utilización de secciones transversales
verticales.
b) Calcule la integral en a).
c) Sea S el sólido de revolución por la rotación de R en torno al eje x. Plantee una integral (impropia)
para calcular el volumen de S
d ) calcule la integral en c).
11. determine le volumen que se genera al rotar el área encerrada por las gráficas de x = y 2 y x = 2 − y 2
en torno al eje x = a; a ≤ 0
12. La región del plano encerrada por la elpise x2 +
integración el volumen generado.
y2
9
= 1 se rota en torno al eje Y . Encuentre mediante
13. determine el volumen generado al rotar la región encerrada por
y = x2 , y = −x + 6
en torno al eje x = 3.
14. Hallar el volumen de la intersección de dos cilindros de igual radio cuando sus ejes se intersectan en
ángulo recto.
15. Encuentre el volumen del sólido obtenido al girar alrededor del eje y la región limitada por las siguientes
curvas:
y 2 = x ; x = 2y
16. Encuentre el volumen del sólido de revolución que se obtiene al rotar la región encerrada por y 2 = x e
y = x3 en torno a la recta x = −1.
17. Hallar el volumen del sólido generado cuando la región encerrada por y = x2 e y = x + 2, gira elrededor
de la recta x = −1
18. Calcule el volumen V del sólido generado al rotar el triángulo acotado por: x = 0, y = 0 e 2x + y = 2
alrededor de la recta x = −1
2
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
19. La región limitada por las gráficas de
y = (x − 1)2
;
y =1+x
se hace girar alrededor del eje x = −2. Hallar el volumen resultante.
20. Encuentre el volumen del sólido generado al girar en torno a la recta x = −1 la región encerrada por
x = 0, x = 2π y la curva y = 1 + sin x.
21. Determine el volumen del sólido de revolución generado al rotar la curva y = e−x sin x , x ∈ [0, 2π[ en
torno al eje y.
22. Considere la región acotada por las curvas y = cos x; y = 1; x = π2 . Determine el volumen del sólido de
revolución que se obtiene rotando la región acotada alrededro del eje x.
23. Encontar el volumen del sólido generado al rotar alrededor de la recta x = −4 la región acotada por
las dos parábolas x = y − y 2 e x = y 2 − 3.
24. Considere la parábola y 2 = x + 2 y la recta y = x − 4.
a) Calcule el área de la región acotada por la parábola y la recta.
√
b) Dibuje la región R encerrada por y = x + 2, la recta y = x − 4 y la recta y = 2.
c) La región R anteriormente dibujada, gira alrededor del eje x. Calcule el volumen del sólido de
revolucióon que se genera.
25. Plantear integrales que permiutan calcular el volumen generado al rotar la región del plano encerrada
por: y = x2 , y = x3 , en torno a:
a) el eje Y .
b) la recta x = 1
(no resuelva las integrales)
26. Encuentre el volumen del sólido de revolución que se genera de la rotación alrededor del eje y de la
región plana acotada por la gráfica de las ecuaciones:
√
y = x; y = 0; y = 1 − x
√
27. La región acotada por las gráficas de y = sin x e y = 1/ 2 entre x = π/4 y x = 3π/4 gira alrededor de
la recta x = π. Calcule el volumen del sólido resultante.
28. Determine el volumen del sólido generado al girar la región encerrada por x = 12(y 2 − y 3 ); x = 0; y = 0
en torno a la recta y = 1.
29. La región infinita acotada por los ejes coordenados y la curva y = −lnx, en el primer cuadrante, gira
sobre el eje x para generar un sólido. Halle el volumen del sólido.
30. Determine el área bajo la curva y =
lnx
x2
desde x = 1 hasta x → +∞
31. Encuentre el volumen del sólido de revolución que se genera de la rotación alrededor del eje y de la
región plana acotada por la gráfica de las ecuaciones:
√
y = x; y = 0; y = 1 − x
32. Halle el volumen de un sólido cuya base sea un disco de radio 5 y cada sección transversal perpendicular
al eje x sea un cuadrado.
3
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
33. Sea R la región encerrada por
y=
1
,
(1 + x2 )2
x2 = 1 y la recta y = 0.
Halle el volumen del sólido producido por la rotación R en torno al eje y.
34. Encontrar el volumen del sólido de revolución, generado por la región encerrada por y = x2 e y = 4, al
rotar elrededor de la recta y = −1.
35. Dadas las semi-circunferencias
c1 : x2 + y 2 = 9,
2
c2 : (x − 2) + y 2 = 1,
y≥0
Encuentre el volumen del sólido generado por la rotación del área interior a c1 y exterior a c2 , alrededor
del eje x.
36. Calcule el volumen del sólido que se obtieneal rotar la región plana encerrada por:
y = 1 + sin x,
y = 0,
x = 0,
x = 2π
en torno a la recta :x = −1.
37.
a) Calcule el centroide de la región acotada por y = sin x, x ∈ [0, π], y el eje x.
b) Determine el volumen del sólido generado al rotar la región anterior en torno de y = −x.
38. Considere la región limitada por las curvas:
y2
x2
+
= 1,
9
4
x=
9 2
y ,
32
y≥0
Exprese las integrales que determinan:
a) El perı́metro de la región encerrada.
b) Volumen que se obtiene al rotar la región en torno a y = −1
c) Volumen que se obtiene al rotar la región en torno al eje y.
d ) Área superficial del sólido obtenido en c).
39. Establezca sin evaluar, la integral que da el área de la superficie de revolución, generada al girar el arco
de y = x3/2 , x ∈ [1, 4], en torno a la recta x = −2.
40. la superficie encerrada por x = y 2 ; x = 8 − y 2 , gira en torno de x = −1. Encuentre el volumen del
sólido ası́ formado.
41. calcular la superficie total del sólido generado por la rotación, en torno al eje x, de la región limitada
por las curvas:
y 2 = 4x e y 2 = 3 + x
42. Calcular el área de la superficie de revolución, generada por los arcos de la parábola
x = y 2 + 2y,
3 ≤ x ≤ 35
al rotar alrededor de la recta y = 10.
43. Exprese mediante integrales el área de la superficie de revolución generada al rotar la parábola y =
x2 − 5x + 6, en torno al eje X para x entre 2 y 3.
44. Establezca sin evaluar, la integral que da el área de la superficie de revolución, generada al girar el arco
de y = x3/2 , x ∈ [1, 4], en torno a la recta x = −4.
4
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
45. Sea R la región del plano encerrada por y = x2 y y = x3 .
a) Calcular el volumen del sólido de revolución obtenido al girar R en torno a:
i) eje OY
ii) x = 1
b) Exprese mediante integrales el perı́metro de la región R.
√
46. La región R está limitada por y = x2 e y = x. Entonces:
a) Calcule el área de la región R.
b) Pruebe qu la distancia del centroide de R a la recta y = x − 3 es
3
2
√
2.
c) Calcule por Pappus el volumen obtenido al rotar R en torno a la recta y = x − 3.
47. Una lámina delgada tiene la forma de un cuadrado de lado 2a, de una de sus esquinas se ha cortado un
cuadrante de cı́rculo de radio a. Hallar el centroide de la región resultante.
48. Determine el área de la región Rn acotada por la gráfica de las ecuaciones
y = x;
y = xn ;
x≥0
para todo valor de n ∈ N.
a) Calcular el centro geométrico Cn = (xn , y n ) de la región Rn .
b) Calcular (si existe)
lı́m xn
n→+∞
;
lı́m y n
n→+∞
49. Encontrar el centroide del anillo:
1 ≤ x2 + y 2 ≤ 2,
x, y ≥ 0
50. Sea α una constante mayor o igual a uno. Sea R la región bajo y = xα , sobre el eje x, entre las rectas
x = 0 y x = 1. Calcule el centroide (x, y) de R. Halle:
lı́m x ;
n→+∞
lı́m y
n→+∞
51. Encontrar el centroide de la región acotada por las curvas y = x2 y la recta y = 2x + 3.
52. Calcule el centroide C = (x, y) del área encerrada por y = 4x − x2 .
53. Determine el centro geométrico de la región plana limitada por las rectas
√
x = 1/ 2, x = 1, y = x, y el arco x2 + y 2 = 1
54. Determine le centroide de la región limitada por la curva
y = 1 − x2 , y la recta y = 0
55. Encuentre el centroide de la región
R = {(x, y)/0 ≤ x ≤ 5/2; x/2 ≤ y ≤ 3x − x2 }
56. Determine el volumen de un sólido cuya base es un cuadrilétero con vértices (3, 0), (0, 3), (−3, 0), y
(0, −3) y cuyas secciones transversales perpendiculared al eje x son semi-cı́rculos.
57.
a) Calcule el centroide de la región acotada por y = sin x, x ∈ [0, 2π], y el eje x.
b) Determine el volumen del sólido generado al rotar la región anterior en torno de y = −x.
5
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
58. Si el centroide de la región plana acotada por la parábola y 2 = 4x y la recta x = b, (b > 0), es el punto
C = (1, 0), calcular b.
59. Calcular el centroide de la región plana limitada por las curvas:
y = x2 − 4
e
y = 2x − x2
60. Determinar el centroide de la región limitada por las parábolas de ecuaciones:
y = x2 − 4
e
y = 2x − x2
61. Una curva de ecuación y = f (x) pasa por el origen. Por un punto arbitrario de la curva se trazan rectas
paralelas a los ejes coordenados del plano cartesiano, formándose de este modo un rectángulo con los
ejes coordenados.
Si la curva divide a dicho rectyángulo en dos regiones cuyas áreas están en la razón 1 : a con a > 0.
Hallar la(s) curva(s).
62. Encuentre la longitud de la curva
y=
1 2
(x + 2)3/2
3
desde x = 0 hasta x = 3.
63. Considere la prábola y = x2 − 2 y la recta y = x + 4
a) Calcule el área encerrada por ambas curvas.
b) Si la región anterior gira en torno al eje x = −10 ¿qué volumen engendra?.
64. Dada la región del plano limitada por los gráficos (y sólo por ellos) de:
i) y ≤ x2
ii) y ≤ 1/x
iii) x ≤ 3
iv) y ≥ 0
Se pide escribir la(s) integral(es) con su(s) respectivos lı́mites de integración que permitan calcular (no
se pide resolver la(s) integral(es)):
a) el área de la región.
b) el perı́metro del área dada en a).
c) el volumen que se genera al rotar la región dada en a) en torno a la recta y = 2.
d ) el volumen que se genera al rotar la región dada en a) en torno a la recta x = −2.
e) la superficie total (interna, externa y lateral) del volumen obtenido en c).
65. Calcule el volumen obtenido por la rotación de la región encerrada por y = ex , y = e−x y el eje OX,
en torno a OX.
66. Calcular el volumen generado al rotar, en torno al eje y, el área limitada por las curvas:
y = 3; x = 3; x = 9; y =
2p 2
x −9+3
3
67. Calcular el volumen generado por la región limitada por la parábola: y = −x2 − 3x − 6 y la recta
y = 3 − x, añ rotar alrededor de la recta x = 3.
6
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
68. Sea R la región plana acotada por las cirvas
y 2 = 4x;
x=
5
3
Determinar:
a) El centroide de R.
b) El volumen generado al rotar R en torno a la recta x = −2.
69. Calcular el volumen encerrado por;
y2
z2
x2
+ 2 + 2 =1
2
a
b
c
a, b, c > 0, distintos entre sı́.
70. Considere la región limitada por
2
y = x (x − 2)
e
y=x
Encuentre:
a) Area de la región.
b) Exprese mediante integrales el perı́metro de la región.
c) Exprese mediante integrales el volumen generado al rotar la figura en torno al eje y = −1.
71. Sea R la región encerrada por las tres curvas siguientes:
√
y = x2 , y = x, y = −x + 6
Exprese las integrales que permiten calcular:
a) El área de la región R.
b) El volumen del sólido de revolución que se genera al rotar la región R en torno al eje x.
72. Hallar el volumen del sólido generado al girar la región entre la parábola x = y 2 + 1 y la recta x = k,
alrededor de la recta x = k; sabiendo que k − 1 ≥ 0. Grafique V(k), es decir, el volumen obtenido en
función de k.
73. Si la densidad de un alambre en [1, 4] es:
(
δ(x) =
2
ex
e(2x−5)
2
;
;
1≤x≤3
3≤x≤4
¿Cuál de los dos tramos del alambre [1, 3] ó [3, 4] es el que tiene mayor masa?
74. Sea C la curva del plano definido por
Z
t
x(t) =
1
sin u
du
u
Z
y(t) =
1
t
cos u
du
u
Sea A = (x(1), y(1)), B = (x(2), y(2)). Calcular la longitud de la curva C desde A hasta B
75. Un punto se mueve sobre una trayectoria dada por
x(t)
y(t)
=
=
2 cos t
1 − cos 2t
Calcule la longitud de la trayectoria
7
t≥0
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
76. Se va a construir una carretera del punto (2, 1) al punto (5, 3) siguiendo la trayectoria de la parábola
√
y = −1 + 2 x − 1
Calcule la longitud de la carretera (las unidades en el eje de coordenadas son millas)
77. Determine la longitud de un arco de la cicloide
x(t)
y(t)
= a(t − sin t)
= a(1 − cos t)
0 ≤ t < 2π
a≤0
78. Se consideran las curvas C1 y C2 dadas en la forma paramétrica mediante
x(t) = t
x(t) = 21 t2
C1 =
1 2 C2 =
y(t) = 2 t
y(t) = t
a) Los segmentos de las curvas C1 y C2 comprendidos entre t = 0 y t = 2 se hace girar alrededor
del eje x, generando dos superficies de revolución S1 y S2 respectivamente. Determine, cuál de las
tres siguientes afirmaciones es verdadera:
Area(S1 ) > Area(S2 ) Area(S1 ) < Area(S2 ) Area(S1 ) = Area(S2 )
b) Justifique claramente su respuesta dada en el item anterior.
79. Hallar el área de la superficie engendrada por un arco de la cicloide
3(t − sin t)
3(1 − cos t)
x =
y =
Al girar alrededor del eje OX
80. Calcular la longitud del arco de curva
Z
t
x(t) =
1
cos z
dz
z
t
Z
y(t) =
1
sin z
dz
z
entre el origen y el punto más cercano donde tenga una tangente vertical.
81. Encuentre el área A de la región que está dentro de ρ = 1 + sin θ y fuera de ρ = 1 − cos θ y encima de
la lı́nea θ = 0
82. Determine el área de la región que es interior a la circunferencia ρ = 3 cos θ y la cardioide ρ = 1 + cos θ
83. Encuentre el área interior a la lemniscata ρ2 = 2 cos θ y exterior a ρ = 1
84. Encuentre la longitud de la gráfica de r = a sin3 ( θ3 )
85. Calcular el área de la región interior a ambas curvas:
r
r
=
2a cos(4θ)
√
= a 2
a>0
86. Encuentre el área de la superficie de revolución generada al girar la parte superior de la gráfica r =
1 + cos θ alrededor del eje polar
87. Considere la hipérbola de ecuaciones paramétricas:
x(t) = cos ht
C:
y(t) = sin ht
t∈R
Compruébelo, por integración, que el área encerrada por C, el semieje positivo OX y la recta por el
origen O y el punto P = (cos hT, sin hT ), T ∈ R, es igual a T /2
8
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
88. Calcule la longitud de la cardioide r = 2(1 + cos θ)
89. Si las ecuaciones paramétricas de una curva son
x(t) = f 00 (t) cos t + f 0 (t) sin t
y(t) = f 00 (t) sin t − f 0 (t) cos t
Pruebe que la longitud de t1 a t2 está dada por
t2
L = f (t) + f 00 (t)
t1
90. Sea R la región a ρ1 (θ) = cos θ y exterior ρ2 (θ) = 1 − cos θ
a) Haga un dibujo aproximado de las figuras
b) Calcule el área de la región R
91. Encontrar el área plana interior a la rosa de 4 hojas: r = 2a cos 2θ y exterior a la curva r = a
a>0
92. Considere en coordenadas polares las curvas
C1 :
r = 3 sin θ
C2 :
r = 1 + sin θ
a) Determine una integral (no la calcule), que permita calcular la longitud de C2
b) Encuentre la pendiente de la recta tangente a C2 en θ =
π
3
c) Determine el área de la región que se encuentre dentro de C1 y fuera de C2
93. Plantee las integrales que permitan calcular el perı́metro de la elipse dada por:
x(t) = 2 cos t
C:
y(t) = 3 sin t
(no calcule las integrales)
94. Un vaso que tiene la forma de un cilindro circular recto de radio R y altura H se encuentra originalmente
lleno de agua. Si el vaso gira alrededor a su eje principal, pierde parte de su contenido y la superficie
libre del lı́quido adopta la forma de un paraboloide de revolución. Para el vaso girando, calcule la
distancia del vértice del paraboloide al fondo del vaso para que se mantenga en rotación la mitad del
contenido original de agua.
95. Encuentre el área de la superficie generada al girar el lazo derecho de la lemniscata en coordenadas
polares r2 = cos(2θ), o bien, en coordenadas paramétricas
p
−π
θ
x(t) = pcos(2θ) cos(θ)
≤θ≤
y(t) =
cos(2θ) sin(θ)
4
4
alrededor del eje y
96. Bosqueje y encuentre el área exterior a la curva r = 1 + cos θ e interior a x2 + y 2 = 9
97. Calcular el área común de la Limacon de Pascal r = 2a + a cos θ y la cardioide r = a(1 − cos θ), con
a>0
98. Demuestre, usando coordenadas polares que el área A del triángulo rectángulo con uno de sus catetos
de medida igual a k viene dado por
Z
k α 2
A=
sec θdθ
2 0
sin calcular la integral. α corresponde al ángulo adyacente al cateto de medida k. Ayuda: Escriba en
polares la ecuación de la recta x = cte
9
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
99. Calcular el perı́metro exterior de la región determinada por las curvas r = 3 cos θ y r = 1 + cos θ
100. Calcular el volumen del sólido obtenido al girar el área encerrada por las curvas.
1. y = ex
2. y = e−x
entre x = 1 y x = 2 en torno al eje de coordenadas (x = 0).
Solución:
Método de cilindros:
h(x) = ex − e−x
Z 2
2
2πx · h(x)dx =
2πx · (ex − e−x )dx
Z
V =
1
1
2
= 2π xex − ex + xe−x + e−x 1
= 2π 2e2 − e2 + 2e−2 + e−2 − 1e1 + e1 − 1e−1 − e−1
2π e2 − 3e2 − 2e−1 ∼
= 44, 355
101. Calcular las coordenadas del centroide de la superficie interior a las dos parábolas:
1. y = 2x2
√
2. y = 2x
Solución:
Puntos de intersección:
2x2 =
√
2x =⇒ x = 0 ∨ x = 2−1/3
=⇒ y = 0 ∨ y = 21/3
√
Z 2−1/3 √
2 2 −1/3 3/2 2 −1/3 3
1
A=
2x − 2x2 dx =
2
2
−
=
3
3
3
0
R 2−1/3
xdA
x= 0
A
√
Z 2−1/3 √
2 2 −1/3 5/2 1 −1/3 4
2
A·x=
x
2x − 2x dx =
2
−
2
5
2
0
9 √
3
=⇒ x =
4
40
Z −1/3 √ 2
1 2
1 −1/3 2 4 −5/3
2 2
A·y =
2x − 2x
2
− 2
dx =
2 0
2
5
√
9 3
=⇒ y =
2
20
102. Un cilindro de radio ”a” y altura ”h” es coronado superiormente por una semi esfera de radio ”a”.
Calcular el momento de innercia de este cuerpo respecto del eje del cilindro.
Solución:
IT otal = ICilindro + ISemiesf era
ICilindro :
Z
ICilindro =
dV = 2πrhdr 0 ≤ r ≤ a
Z a
Z
r2 dA =
r2 2πrhdr = 2πh
0
0
10
a
r3 dr = 2πh
a4
4
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
ICilindro =
πha4
2
ISemiesf era :
r2 + z 2 = a2 =⇒ 2rdr = −2zdz
Z
ISemiesf era =
r2 dV = −2
Z
dV = z2πrdr = −2πz 2 dz
Z a
3
2
2
a5
2
2
2 2
4
2 a
a − z πz dz = 2
a z − z πz dz = 2π a ·
−
3
5
0
0
a
4πa5
ICilindro =
15
h
4
∴ IT otal = πa4
+ a
2
15
103.
a) Sea S la región del plano limitada por las curvas y = x3 , y = x, x > 0. calcule el volumen del
sólido de revolución generado al rotar S en torno a la recta x = 1.
b) Determine las coordenadas del centroide de la región acotada por y 2 = 2px, p > 0, y > 0 y las
rectas y = 0, x = 1.
Solución:
a)
Z
V = 2π
0
1
x3
x4
x5
x2
−
−
+
(1 − x)(x − x )dx = 2π
2
3
4
5
3
1
7
7π 3
=
[u ]
= 2π
60
30
0
b)
1
2p
2
Z
1
p
2
0
√
Z 1p
2 2p
5/2
My =
2px dx =
5
0
√
Z
1√
p
2 2p
A = 2p
xdx =
3
0
√
My
Mx
3
3 2p
∴x=
= ; y=
=
A
5
A
8
Mx =
xdx =
104. Sea R la región en el semiplano {(x, y) ∈ R2 /x ≥ 0}, limitada por las curvas y = ex , y = cos x y la
recta x = 2π.
a) Calcular el área de la región R
b) Escriba la integral que determina el volumen del sólido generado por R al rotar en torno:
i) al eje y
ii) a la recta y = −1
Solución:
a)
Z
A=
2π
(ex − cos x) dx =
0
Z
2π
ex dx = e2π − 1
0
b)
Z
2π
V = 2π
0
11
x (ex − cos x) dx
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
c)
2π
Z
(ex + 1)2 − (cos x + 1)2 dx
V =π
0
105. Calcular el volumen generado al rotar, la región del plano encerrada por: y = x2 , y = x3 , en torno a:
a) el eje OY .
b) la recta x = 1.
Solución:
a)
Z
1
Vy = π
Z
ydy + π
0
1
y 2/3 dy = π/10
0
b)
Z
1
(1 −
Vx=1 = π
√
1
Z
2
y) dy − π
1 − y 1/3
2
dy = π/6 − π/10 = π/15
0
0
106. Calcular la longitud del arco de la curva:
Z
x
y=
p
t2 + 2tdt
0
entre los puntos para los cuales x = 0 y x = 1.
Solución:
√
tenemos que y 0 = x2 + 2x, luego:
Z 1p
Z
l=
1 + y 02 dx =
0
1
Z 1
p
1 + x2 + 2xdx =
(1 + x)dx = 3/2
0
0
107. Encuentre el centroide del semicı́rculo: x2 + y 2 = 1, y ≥ 0, y utilice el teorema de Pappus para calcular
el volumen del sólido que resulta al rotar el semicı́rculo en torno a la recta y = −1
Solución:
Sea C = (x, y) el centroide, por simetrı́a: x = 0
Z
Z 1
Z 1 p
1
2
2
ydA = 2
yxdy = 2
y 1 − y 2 dy = − (1 − y 2 )3/2 =
3
3
0
0
0
Z
π
2/3
4
4
dA =
∴y=
=
∴ C = 0,
2
π/2
3π
3π
Por el Teorema de Pappus:
4
V = 2π 1 +
3π
4
A = 2π 1 +
3π
π
=π
2
4 + 3π
3
108. Encontrar las coordenadas del centroide de la región encerrada por la curva y =
Solución:
Es preciso, para calcular el área, evaluar una integral impropia:
Z +∞ A
x2 − 1
=
1− 2
dx = π =⇒ A = 2π
2
x +1
0
x2 −1
x2 +1
Cálculo del momento con respecto al eje x, (pues x = 0):
Z +∞ Z +∞
1
x2 − 1
x2 − 1
2x2
Qx =
1+ 2
1− 2
dx =
2 dx
2
x +1
x +1
−∞ 2
−∞ (x + 1)
12
y su ası́ntota.
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
Se debe aplicar integración por partes con:
u=x
Se obtiene:
Qx =
−
lı́m
a → −∞
b → +∞
dv =
2x
(x2
2 dx
+ 1)
π π
x
b
+
arctan(x)
= + =π
x2 + 1
2
2
a
∴y=
π
1
=
2π
2
Luego, el centroide está en:
C=
1
0,
2
2
109. Calcule el volumen del sólido que se obtiene al girar la región limitada por la semi-elipse x4 + y 2 =
1, y ≥ 0 y la semi-circunferencia x2 + y 2 = 4, y ≤ 0, en torno a la recta que pasa por los puntos
(−3, 0) y (0, −4) Solución:
Ecuación de la recta l:
y
x
+
= 1 =⇒ 4x + 3y + 12 = 0
−3 −4
Area de la región:
π + 2π = 3π
Centroide de la región:
r
p
x2
; y2 = − 4 − x2
4
Z 2 Z 2
y1 + y2
1
x2
1
3 2
2
(y1 − y2 ) dx =
1−
− 4−x
dx =
x − 3 dx
2
6π −2
4
6π −2 4
1
4
1 x3
2
− 3x =
(4 − 12) = −
=
6π 4
6π
3π
−2
1−
y1 =
1
3π
Z
2
−2
Distancia desde el centroide a l:
4
− π + 12
12π − 4
d = d(Rc , l) = √
=
5π
16 + 9
Pappus:
V = 2πdA =
24π
(3π − 1) [u3 ]
5
110. Sea α una constante mayor o igual a uno. Sea R la región bajo y = xα , sobre el eje x, entre las rectas
x = 0 y x = 1. Calcule el centroide (x, y) de R. Halle:
lı́m x ,
lı́m y
α→+∞
α→+∞
Solución:
El área de la región es:
Z
A=
1
xα dx =
0
1
α+1
El momento con respecto al eje y es:
Z
My =
1
x · xα dx =
0
Z
0
13
1
xα+1 dx =
1
α+2
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
El momento con respecto al eje x es:
1
Z
y · xα dx =
Mx =
0
1
Z
x2α dx =
0
1
4α + 2
Las coordenadas del centroide son:
(x, y) =
My Mx
,
A A
=
α+1 α+1
,
α + 2 4α + 2
Por lo tanto:
lı́m x = 1 ,
α→+∞
lı́m y =
α→+∞
1
2
111. Determinar el centroide de la región limitada por las curvas y 2 = 8 · x y x2 = y Solución:
√
dA =
8x − x2 dx
Z
2
A=
√
8x − x2 dx =
0
R2
x=
0
x
√
2 √ 3/2 x3
8x −
3
3
2
16 8
8
− =
=
3
3
3
0
2
8x − x2 dx
3 25
3 2 √ 5/2 x4 24
9
=
8x −
−
=
=
8/3
8 5
4 8 5
4
10
0
3
y=
8
Z
0
2
√
8x + x2
2
!
√
2
3
3
8x − x dx =
8x − x4 dx =
16 0
16
9 9
∴ Rc =
,
10 5
2
Z
x5
4x −
5
2
2
9
=
5
0
112. Calcular la longitud de arco de:
y = ln
ex − 1
ex + 1
para 1 ≤ x ≤ 3.
Solución:
ex
ex
2ex
−
=
ex − 1 ex + 1
e2x − 1
s
2 Z 3
Z 3 2x
Z 3
2ex
1 p 4x
e +1
2x
2x
1+
=
e − 2e + 4e dx =
dx
y=
2x − 1
2x − 1
2x − 1
e
e
e
1
1
1
6
Z 3
Z 3
3
2e−2x
1 − e−6
e −1
−2x dx = 2 + ln 1 − e
−2
=
dx +
= ln 2
= 2 + ln
−2x
1 − e−2
e −1
1
1
1 1−e
y0 =
113. Dada la función
1√
1+ x
a) Encuentre el área encerrada por la función y = f (x) entre las rectas x = 0 y x = 1.
b) Encuentre la integral que permite calcular nla longitud de arco de la función Y = f (x) para x
entre 0 y 1.
Solución:
14
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
a)
x = u2
u≥0
dx
dx = 2udu
√
A=
x = 0;
u=0
0 1 x
x = 1;
u=1
Z 1
Z 1
Z 1
1
du
2udu
1
1−
du −
=2
du = 2
= 2 (u − ln|1 + u|) = 2 (1 − ln2) [u2 ]
1+u
1
+
u
1
+
u
0
0
0
0
Z
Z
∴A=
0
1
1
b) La expresión mediante integrales de la longitud de arco entre x = 0 y x = 1 es:
Z 1q
Z 1s
1
− 2√
1
1
x
2
0
√ 4 dx
√ 2 =− √
√
f 0 (x) =
l=
1 + (f (x)) dx =
1+
4x(1 + x)
(1 + x)
2 x(1 + x)2
0
0
1
Z
s
∴l=
0
√
4x(1 + x)4 + 1
√
dx
4x(1 + x)4
114. Sea R la región limitada por las curvas:
y = x2 , y = 0, y = (x − 4)
Exprese las integrales que permiten calcular:
a) El área de la región R.
b) El volumen del sólido de revolución que se genera al rotar la región R en torno a la recta x = 4,
mediante el método de los anillos y el método de los cilindros.
Solución:
a)
Z
2
A=
x dx +
0
b)
4
Z
2
(x − 4) dx [u2 ]
2
2
Por anillos:
V =
2
Z
(4 − x) x2 dx + 2π
2π
0
Por cilindros:
V =
Z
π
4
Z
(4 − x)(x − 4)2 dx [u3 ]
2
4
(4 −
√
4
Z
2
y) dy − π
0
(4 − (4 −
√
y)) dy [u3 ]
0
115. Considere la región encerrada por las curvas y 2 = x, y = 2 − x, x = 0. Exprese las integrales, sin
calcularlas, que permiten calcular:
a) El perı́metro de la región encerrada por las curvas.
b) El volumen del sólido generado al rotar la región anterior en torno al eje x = 2.
c) El área lateral del sólido generado al rotar la región anterior en torno al eje x.
Solución:
a)
P =2+
√
Z
2+
r
1+
0
15
1
1
dx
4x
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
b)
Z
1
(2 − x) (2 − x) −
V = 2π
√ x dx[u3 ]
0
c)
Al =
Z
1
2π
Z
√
(2 − x) 2dx + 2π
√
0
0
116. Para la curva:
1
√
x = ln 1 + t2
y = arctan(t)
c:
1
x 1+
4x
dx [u2 ]
t∈R
a) Encuentre los puntos donde C tiene recta tangente vertical y recta tangente con pendiente igual
a 1.
b) Calcule la longitud de arco de C entre los puntos encontrados.
Solución:
a)
dy
dt
dx
dt
1
1+t2
t
1+t2
=
=
)
=⇒
dy
dy/dt
1
=
=
dx
dx/dt
t
Luego:
C tiene tangente vertical para:
dx
dy
=0∧
6= 0
dt
dtY
C tiene tangente con pendiente 1 ⇔
⇔t=0
dy
dx
=1⇔t=1
√
Luego, los puntos buscados son (0, 0) y (ln 2, π/4)
b) Sea l(C) la longitud de arco de C entre los puntos de a). Entonces:
s
2 2
Z 1
Z 1q
Z 1 1
t
dt
2
2
√
+
dt
=
l(C) =
(x0 (t)) + (y 0 (t)) dt =
2
2
1
+
t
1
+
t
1
+ t2
0
0
0
Sea t = tan θ =⇒ dt = sec2 θdθ, t = 0 ⇔ θ = 0, t = 1 ⇔ θ = π/4
π/4
Z
∴ l(C) =
0
π/4
√ sec θdθ = ln| tan θ + sec θ|
= ln 1 + 2
0
117. La parábola y = 19 x2 + 2, une los puntos P = (−3, 3) y Q = (3, 3).
a) Determine (no calcule) una integral que permita calcular la longitud del arco que una P y Q.
b) Determine (no calcule) una integral que permita calcular el área de la superficie que se genera
cuando el arco gira alrededor del eje x.
Solución:
a)
q
2
dl = 1 + (y 0 ) dx =
Z
3
s
1+
l=
−3
16
s
1+
2
2
x dx
9
2
2
x dx
9
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
b)
x2
Z
Z
A=
2πydl =
2πy
1+
−3
x1
Z
s
3
3
2π
=
−3
2
2
x dx
9
s
2
1 2
2
x +2
1+
x dx
9
9
118. Calcular para x ∈ [−1, 1] el valor de:
r
arc cos(x) − 2 arcsin
1−x
2
!
Solución
Sea ϕ = arc cos(x) ⇒ cos(ϕ) = x,
0≤ϕ≤π
Luego:
!
!
r
r
ϕ 1−x
1 − cos(ϕ)
2 arcsin
= 2 arcsin
= 2 arcsin sin
2
2
2
0 ≤ ϕ/2 ≤ π/2
119. Determine el volumen del sólido de revolución generado por el área bajo la curva y = |e−x cos x|, x ≥
π/4, al rotarla en torno al eje x. Justifique adecuadamente.
Z
+∞
V =
Z
2
π/4
Z
+∞
π (f (x)) dx =
πe−2x cos2 xdx = lı́m π
t→+∞
π/4
Z
Z
t
e−2x cos2 xdx
π/4
Z
Z
cos 2x + 1
1
1
dx =
e−2x dx +
e−2x cos 2xdx
2
2
2
1 1 −2x
1
1
1
1 −2x
+
e
(sin 2x − cos 2x) = − e−2x + e−2x (sin 2x − cos 2x)
=
− e
2
2
2 4
4
8
1 −π/2 1 −π/2 1 −2t
e
− e
+ e
(sin 2t − cos 2t − 2)
∴ V = π lı́m
t→+∞ 4
8
8
I=
e−2x cos2 xdx =
e−2x
V =
πe−π/2
8
120. Considere la figura formada por dos semicircunferencias centradas en (4, 2) y de radio 1 y 2 respectivamente y por los trazos rectos que allı́ se muestran. Exprese mediante integrales:
a) El volumen del sólido que se obtiene al girar la figura en torno a la recta x = −2.
b) La superficie del sólido que se obtiene al girar la figura en torno a la recta y = 7.
Solución:
p
4 − (x − 4)2
p
C2 : y = 2 − 1 − (x − 4)2
C1 : y = 2 +
a) Por anillos:
Z
V = 2π
6
Z 5
p
p
2
(x + 2)(2 − 1 − (x − 4)2 )dx
(x + 2)(2 + 4 − (x − 4) − 2)dx + 2π
3
2
17
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
b)
Z
S = 2π
6
s
7− 2+
p
4 − (x − 4)2
1+
2
Z
+2π
5
s
p
7 − 2 − 1 − (x − 4)2
1+
3
(x − 4)2
dx
4 − (x − 4)2
(x − 4)2
dx + 4π
1 − (x − 4)2
Z
3
p
(7 − 2) 1 + 02 dx
2
121. ¿Qué % del volumen
del cilindro de la figura queda dentro del volumen engendrado por la rotación de
p
la curva y = 8 1 − xb ?
Solución:
Intrersección de la curva con los ejes:
x y
0 1
b 0
VCilindro = π · 1 · b = π · b
r
2
1/4
Z b
Z b r
x
x
4
8
=π
1−
dx =
1−
dx = πb
b
b
5
0
0
VRegion
π 45 b
= 80 %
πb
122. Calcular el volumen generado por la rotación de la región encerrada por las curvas: y = ex , y = e2x ,
y = 4, en torno a la recta y = 4.
Solución:
Z
ln2
V =π
(4 − ex )2 − (4 − e2x )2 dx + π
0
Z
V =π
Z
ln4
(4 − ex )2 dx
ln2
ln2
−8ex + 9e2x − e4x dx + π
0
Z
ln4
(16 − 8ex + e2x )dx
ln2
e2x ln4
1
9
ln2
)
V = π −8ex + e2x − e4x + π(16x − 8ex +
2
4
2 ln2
0
33
V = 19ln2 −
π
4
123. La figura muestra un tronco de cono circular con un agujero cónico circular a lo largo de su eje. calcule
el volumen por integración Solución:
El sólido puede considerarse como generado por la rotación, en torno al eje OX de la región achurada
en la figura, donde:
2
1
l1 (x) = x + 4
l2 (x) = x + 1
5
5
2
2 #
Z 10 " Z 10 2
1
3 2 14
∴V =
π
x+4 −π
x+1
dx = π
x + x + 15 dx
5
5
25
5
0
0
124. Determine el área que se encuentra bajo la recta
√
Solución:
18
3y = x y dentro de la cardioide r = 2(1 + cos θ)
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
Se tiene que el área es A =
A =
1
2
Z
=
=
=
=
1 2
r dθ
π+π/6 2
+
R π/6
2π
2
1 2
2 r dθ
0
1
2 (1 + cos θ) dθ + · 4
2
π+π/6
Z
=
R 2π
2
Z
π/6
(1 + cos θ)2 dθ
0
2π
π/6
Z
cos 2θ
)dθ
2
π+π/6
0
2π
2π
h3
i
1
3π
1
2 (2π − π − π/6) + 2 sin θ
+ sin 2θ
+
+ 2 sin π/6 + sin 2π/6
2
4
26
4
π+π/6
π+π/6
i
h5
1
π
1
2 π + 2 sin π6 − sin π/3 + + 2 sin π/6 + sin π/3
4
4
4
4
3
2( π + 2)
2
(3π + 4)
2
(1 + 2 cos θ + 1/2(1 + cos 2θ))dθ +
(3/2 + 2 cos θ +
125. Calcule, por integración en coordenadas polares, el área del cı́rculo: ρ = cos θ + sin θ
Solución:
Intersección con los ejes: θ = 0 ⇒ ρ = 1, θ = π/2 ⇒ ρ = 1 por otro lado ρ = 0 ⇔ cos θ + sin θ = 0 ⇔
θ = −π/4, 3π/4
Z π/4
1 2
ρ dθ
A =
−π/4 2
Z
1 3π/4
=
(cos θ + sin θ)2 dθ
2 −π/4
Z
1 3π/4
(1 + sin 2θ)dθ
=
2 −π/4
i3π/4
1h
1
=
θ − cos 2θ
2
2
−π/4
π
=
2
126. Sea R la región exterior a r = sin θ e interior a r = 1 + cos θ, situada sobre el eje polar. Calcule la
superficie lateral del sólido obtenido al girar R en torno al eje polar
Solución:
Sea S el área de la superficie lateral del sólido, entonces
1
1
1
S = · 2π · · 2π · +2π
2
2
2
|
{z
}
π/2
Z
r2 sin θds
0
P appus
ó
Z
π/2
S = 2π
Z
r1 sin θds + 2π
0
S
=
=
=
=
π2
+ 2π
2
Z
π/2
r2 sin θds
0
π/2
(1 + cos θ) sin θ
q
(1 + cos θ)2 + sin2 θdθ
0
√ Z π/2
π2
+ 2π 2
(1 + cos θ)3/2 sin θdθ
2
0
√
π/2
π2
4π 2
−
(1 + cos θ)5/2 2
5√
0
π2
4π 2 32π 2
−
+
[u ]
2
5
5
19
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA
Departamento de Matemática
127. Calcule el área que se encuentre fuera de la circunferencia r =
9 cos 2θ
p
9/2 y dentro de la lemniscata r2 =
Solución:
Intersecciones: 9 cos 2θ = 9/2 de modo que cos 2θ = 1/2 2θ = π/3 θ = π/6, luego por la simetrı́a se
tiene
Z π/6
1 π/6
2
)dθ
(r
− rN
A/2 = 2
2 +∞
0
Z π/6
=
(9 cos 2θ) − 9/2)dθ
0
=
=
=
=
=
A =
π/6 9 π/6
9
− θ
sin 2θ
2
2 0
0
9
9π
sin π/3 −
2
26
9√
3
3− π
4√
4
9 3 − 3π
4
3 √
(3 3 − π)
4
3 √
(3 3 − π)
2
20