tercer año
Anuncio
Tercer año
Examen Eliminatorio
TEMA
TERCER AÑO
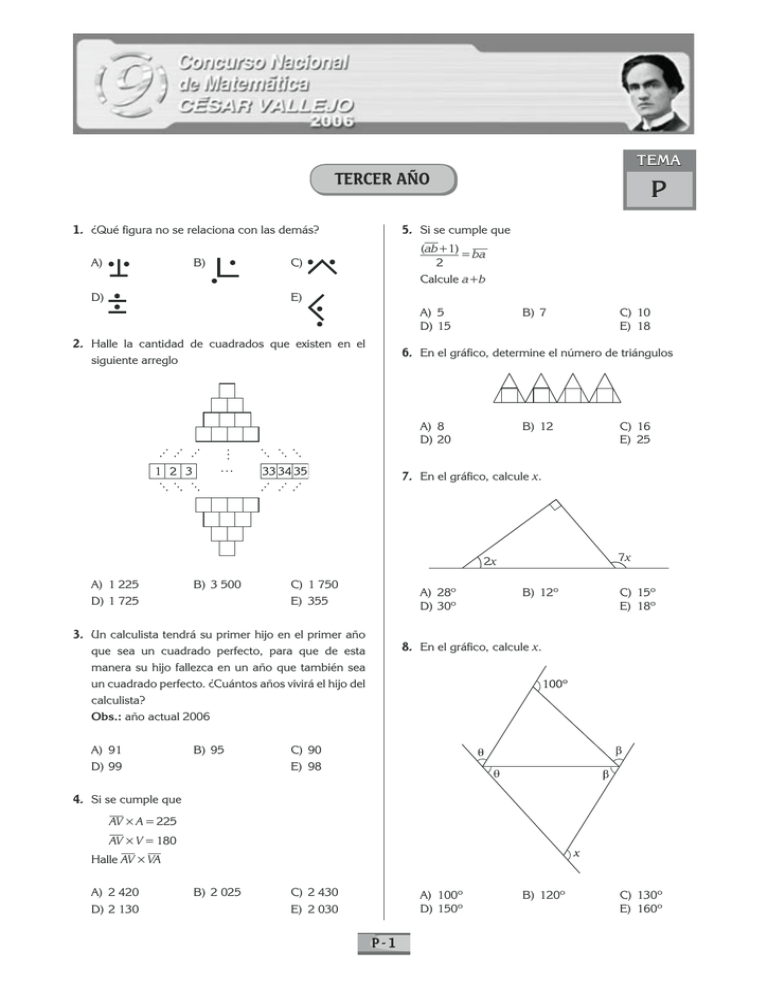
1. ¿Qué figura no se relaciona con las demás?
A)
B)
D)
P
5. Si se cumple que
(ab+1)
= ba
2
Calcule a+b
C)
E)
A) 5
D) 15
2. Halle la cantidad de cuadrados que existen en el
siguiente arreglo
B) 7
C) 10
E) 18
6. En el gráfico, determine el número de triángulos
A) 8
D) 20
B) 12
C) 16
E) 25
7. En el gráfico, calcule x.
7x
2x
A) 1 225
D) 1 725
B) 3 500
C) 1 750
E) 355
A) 28º
D) 30º
3. Un calculista tendrá su primer hijo en el primer año
que sea un cuadrado perfecto, para que de esta
manera su hijo fallezca en un año que también sea
un cuadrado perfecto. ¿Cuántos años vivirá el hijo del
calculista?
Obs.: año actual 2006
A) 91
D) 99
B) 95
C) 90
E) 98
B) 2 025
C) 2 430
E) 2 030
B) 12º
C) 15º
E) 18º
8. En el gráfico, calcule x.
4. Si se cumple que
AV × A = 225
AV × V = 180
Halle AV × VA
A) 2 420
D) 2 130
A) 100º
D) 150º
P-1
B) 120º
C) 130º
E) 160º
Concurso Nacional de Matemática CÉSAR VALLEJO 2006
9. El jardín de Luis, es de forma triangular, asimismo
tiene un árbol en cada esquina y cuatro árboles en
cada lado. ¿Cuántos árboles tiene el jardín de Luis?
A) 15
D) 10
B) 12
14. Un agricultor antes de cultivar su tierra de 6 hectáreas
calculó que por hectárea necesitaba en semillas,
abono y tractor S/.800 en total. Al cosechar gastó
S/.250, asimismo al poner sus productos a la venta
obtuvo por hectárea S/.4 700 y pagó el 10% de
impuesto sobre el precio de venta. ¿Cuánto ganará
en total, si al sembrar no utilizó dos hectáreas?
C) 11
E) 9
10. En el gráfico mostrado, calcule a – b.
A) S/.18 800
D) S/.14 600
B) S/.7 300
C) S/.6 360
E) S/.12 720
15. Fabrizio inició un negoció con S/.8 000, luego de
5 meses ingresa Jesús como socio, aportando al
negocio un capital de S/.2 500, fue en tal ocasión
cuando Fabrizio se retiró del negocio. Si el negocio
liquidó a los 15 meses de iniciado, determine en
qué relación estarán la ganancia de Fabrizio y Jesús,
respectivamente.
A) 30º
D) 72º
B) 80º
A) De 3 a 8
D) De 8 a 5
C) 36º
E) 75º
B) 3
B) 18
Indique la suma de elementos de A.
A) 9
D) 21
C) 17
E) 57
B) S/.900
B) 12
C) 19
E) 20
17. Dado el conjunto
B= x ∈ Q/
3
1
≤x≤
5
5
Si B se divide en cinco partes iguales el punto medio
del cuarto intervalo es
A) 2/5
D) 3/25
C) 20
E) 19
B) 7/25
C) 12/25
E) 4/25
18. Dado los números {x; y; z} ⊂ R, tal que x2 < y2< z2;
z < y < x; xyz > 0. Indique el valor de verdad de las
siguientes proposiciones.
13. Un comerciante adquiere 110 televisores, todos
del mismo precio, para ofrecerlos al público fija el
precio aumentando el costo en 20%, pero durante la
primera semana del mundial Alemania 2006 ofreció
una rebaja del 5%, la segunda semana 10% y la
tercera semana 15%. Vendió 10; 20 y 80 televisores,
respectivamente, por semana y ganó S/.3 680. ¿Cuál
fue el precio de costo de cada televisor?
A) S/.800
D) S/.1 000
x+1 + 6–x ∈ R
A= x ∈ Z/
12. En una obra trabajan Santiago y su nieto, la eficiencia
de Santiago y de su nieto estan en la relación de 5
a 3 respectivamente. Si juntos realizaron la obra en
9 días, ¿en cuántos días terminaría la obra Santiago
trabajando solo y disminuyendo su eficiencia en 20%?
A) 16
D) 17
C) De 5 a 3
E) De 5 a 2
16. Dado el conjunto
11. Se reparte S/.1 800 entre cinco hermanos
proporcionalmente a sus edades que son 24; 18; ab;
15; ba años. Si el que tiene 24 años recibe S/.180
más que el que tiene 15 años, calcule a + b.
A) 2
D) 145
B) De 5 a 6
I. x + yz > 0
II. xy + xz < 1
III. y + z – x ≥ 2
x y z
IV.
– + < xyz
y z x
A) VVVV
D) VVFF
C) S/.950
E) S/.1 050
P-2
B) FVFV
C) VVFV
E) VFFV
Tercer año
Examen Eliminatorio
A) 16
19. Sean los conjuntos
B) – 6
D) 12
5(x + 1)
+ 2x + 1 > 6
7
B= {x ∈ Z / x2 – 10(x – 2) < 3x – 2}
A= x ∈ R/
C) 9
E) 25
24. Luego de resolver la inecuación irracional.
3
3
4
x –1 + x + x +1 < x + 1 + x + x2 –2x + 1
Indique el número de elementos de A ∩ B.
Indique el complemento del conjunto solución.
A) 8
B) 5
D) 9
C) 7
E) 10
A) ⟨– ∞; 1⟩
B) ⟨– 1; 1⟩
x+1
, halle el menor valor entero que
x–1
verifica la inecuación f(1 – x) < 1.
20. Si f(x) =
A) 0
B) 1
D) 3
C) ⟨– ∞; 1⟩ ∪ ⟨4; + ∞⟩
D) φ
E) R
C) 2
E) 4
25. Si
x0 es solución de |x – a|=|x – b|; a ≠ b
21. Dada la ecuación |x2 – a|= b cuyo conjunto solución
x1 es solución de |x – a|=|x – x0|
tiene tres elementos. Indique la relación entre a y b.
A) a + b = 0
B) a = b = 0
D) a = b
x2 es solución de |x – a|=|x – x1|
C) a = b + 1
E) a + 1= b
xn es solución de |x – a|=|x – xn –1|
halle el valor de xn.
22. Halle (α + 1)–1, si α es solución de la ecuación
|x – 2|+|x – 1| + 4 x2 – 4x + 4 = x – 2 + 2
A) 1
B) 2/5
D) 2/7
A)
2n a + b
2na + b
n
B) (2 –1)na + b
2
C) 7/3
E) 2
n –1
C) 2 an + b
2
23. Sea la ecuación irracional en x.
8x + 2k – 1 = x + k
Si tiene dos soluciones cuya diferencia es 6, indique
el producto de valores de k.
P-3
D)
2n –1 a + b
2n+1
E)
(2n +1–1) a + b
2n+1








