Limitaciones en el análisis de los amplificadores realimentados a

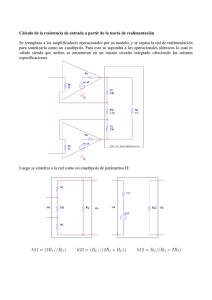
LIMITACIONES EN EL ANÁLISIS DE LOS AMPLIFICADORES REALIMENTADOS A TRAVÉS
DE LA TEORÍA DE REDES DE DOS PUERTOS
Bernardo Meléndez y Carlos Villanueva
Departamento de Electrónica y Comunicaciones Escuela de Ing. Eléctrica. Facultad de Ingeniería.
Universidad de Carabobo Valencia. Edo. Carabobo. Venezuela cvillanu@thor.uc.edu.ve
Resumen
En este artículo se muestran las limitaciones así como el rango de aplicación del método tradicional i análisis de
circuitos amplificadores realimentados transistorizados el cual utiliza la relación a/(1+af) para calcular la
función de transferencia, en comparación con el método general de resolución utilizando las leyes de Kirchhoff.
Se presenta una breve descripción del método tradicional de análisis, así como de los supuestos en los cuales es
basado. Se efectúan dos ejemplos de aplicación, uno de los cuales cumple con dichos supuestos y donde se
verifica validez del método tradicional con respecto al método de Kirchhoff, y otro donde no se cumplen,
dándose el grado error cometido en el cálculo de la ganancia y la resistencia de entrada del amplificador si de
todas maneras se utiliza dicho método, en función de ciertos parámetros de los transistores.
Abstract.- On this paper the limitations and applicable range of the traditional method of analysis of feedback
transistor amplifiers for calculating the transfer function using the relationship a/(1+af) in comparison to the
application of Kirchhoff method is presented. A brief description of the traditional method of analysis and their
assumptions is given. One example is presented where the assumptions are met and identical results are
obtained applying, the traditional method and the Kirchhoff one. A second example is given where eventhough
the assumptions are not met, the traditional method is applied and the result is compared to the Kirchhoff
method, indicating the error degree on the gain amplifier and the input resistance.
Palabras claves: Amplificadores realimentados, Realimentación, Redes de dos puertos, Circuitos
electrónicos, Transistor
Key words: Feedback Amplifiers, Feedback, Two-port networks, Electronics circuits, Transistor.
Este Artículo fue presentado en el IV Congreso Interamericano de Educación en Ingeniería y Tecnología INTER-TECH 96,
Valencia, Venezuela, 22-25 Septiem4 1996; y en la International Conference on Engineering Education: Progress Through
Partnerships, ICEE 97, Chicago, USA, 13-I S Agosto 1997.
INTRODUCCION
El método general de análisis usado actualmente en los circuitos amplificadores realimentados se basa en el
cálculo de la función de transferencia del circuito realimentado total, dada por la ecuación a/(1+af), ecuación
general de los sistemas de control realimentados, calculando la expresión de "a" y de "f " por separado para su
posterior inserción en la expresión general; es de hacer notar que estas funciones de transferencia "a" y " f "
deben ser mutuamente independientes.
Para ello se utiliza la representación más general de un circuito que es la red de dos puertos y el problema se
restringe a la interconexión de dos redes de dos puertos tales como la del circuito "a" y la del circuito " f ", que
en el caso de los circuitos amplificadores realimentados corresponden al amplificador básico y a la red de
realimentación respectivamente. Las funciones de transferencia de estos dos circuitos son mutuamente
dependientes, lo cual no las hace candidatas para ser usadas en la expresión general a / (1+af). Por ello es
necesario transformar dichos circuitos en unas "nuevas" configuraciones de manera que podamos aplicar la
metodología a través de la cual se obtiene la función de transferencia generalizada.
Esta metodología se basa en la manipulación de los parámetros de las redes de dos puertos del circuito
amplificador básico y de la red de realimentación de forma que se constituye un "nuevo" circuito "a" a partir del
amplificador básico original agregándole los efectos de carga de la red de realimentación tanto en la entrada
como en la salida, más los efectos de la fuente de señales y del circuito de carga del amplificador realimentado.
De igual forma la constitución del "nuevo" circuito " f " se hace a partir de uno de los componentes de la red de
dos puertos que representa a la red de realimentación. Esto es, en líneas generales, el procedimiento usado por
los entendidos para el análisis de los amplificadores realimentados.
La limitación que se presenta en este tipo de enfoque para el análisis de los circuitos realimentados estriba en
dos puntos fundamentales. El primero es que no necesariamente el amplificador básico es una red de dos
puertos, tal como sucede en los amplificadores discretos que comparan tensión en la entrada o muestrean
corriente en la salida. El segundo punto es que siendo el amplificador básico y la red de realimentación redes de
dos puertos, su interconexión altera en algunos casos los parámetros de las redes tal como lo demuestran las
Pruebas de Brune. Estas razones hacen que el método no sea válido en todos los casos de amplificadores
realimentados.
Este artículo pretende demostrar el alcance de este método, sus limitaciones y el rango donde se puede utilizar
el mismo aunque se violen las reglas sobre las cuales está basado.
l.- Definición de realimentación negativa:
A partir del diagrama unifilar de un amplificador realimentado mostrado en la Figura 1, se tienen las siguientes
si la red de realimentación y la carga RL no cargan al amplificador básico.
si el amplificador básico y la entrada no cargan a la red de realimentación.
La ecuación (4) constituye la ecuación básica de los sistemas realimentados.
Es importante notar que las funciones de transferencia "a" y " f " se pueden calcular dentro del circuito
realimentado o sacando fuera del sistema al amplificador básico y a la red de realimentación para el cálculo de
las respectivas funciones de transferencia " a " y " f ".
Figura 1: Diagrama unifilar de un amplificador realimentado.
2.- Posibilidades de conexión o topologías en un sistema realimentado.
En la Figura 2 se muestra el diagrama de bloques de un circuito amplificador realimentado, donde se
representan todos los componentes, así como las variables de entrada y de salida respectivas. En general, las
expresiones que relacionan dichas variables son las siguientes:
considerando que " a " y " f " no se cargan mutuamente y además que el generador de señales y la carga no
tienen influencia sobre Xf y X0.
Figura 2: Circuito amplificador realimentado.
Puesto que las variables eléctricas ( Xs, Xi, X0 y Xf) más utilizadas son el voltaje (v) y la corriente (i), la red de
comparación sólo tiene dos posibilidades para construirse, o sea un nodo o una malla. De igual forma la red de
muestreo, con las condiciones impuestas en la Figura 2, sólo puede ser un nodo o una malla. De esta manera se
pueden obtener las cuatro configuraciones básicas de un sistema o circuito realimentado, tal como se muestra en
la Figura 3.
3.- Análisis de los circuitos que utilizan comparación de tensión y muestreo de tensión.
Mientras prescindamos de las cargas mutuas del amplificador básico (AB) y de la red de realimentación (RR),
será posible identificar netamente en un circuito realimentado el AB y la RR, como lo hemos hecho en la Figura
3. Sin embargo, esto no es posible hacerlo en forma general puesto que por ejemplo la RR y la carga determinan
el valor de X0 a través de la expresión a(Xs - Xf). De tal forma que si deseamos utilizar la expresión (7) debemos
rearreglar los circuitos de manera que encontremos un nuevo circuito " a " y un nuevo circuito " f ", donde sus
funciones de transferencia sean mutuamente independientes.
Vamos a desarrollar un método para analizar los circuitos realimentados que posean una topología como la
mostrada en la Figura 3a. Para ello se va a utilizar el método más general de representación de una estructura
circuital, como lo son el AB y la RR, a través de una red de dos puertos, lo cual impone ciertas restricciones al
método pues no necesariamente una red de cuatro terminales, tal como lo son el AB y la RR, es una red de dos
puertos.
3.1.- Análisis en función de redes de dos puertos.
a) Para generalizar el análisis utilizaremos redes de dos puertos para cada bloque (AB y RR).
b) Encontraremos la función de transferencia X0 / Xs = V0 / Vs a partir de las leyes de Kirchhoff.
c) A este resultado le daremos la forma de a / (1+af).
Figura 3: Las cuatro topologías básicas de amplificadores realimentados.
d) Por inspección determinaremos quien es " a " y quien es " f y cual es su significado en términos de los
parámetros del AB de la RR.
e) Se comprobará que los nuevos circuitos " a " y " f " son mutuamente independientes y que cumplen con todas
la condiciones impuestas en la ecuación general a / ( 1+af).
La estructura más apropiada de red de dos puertos para resolver el circuito de la Figura 3a, es aquella en la cual
los parámetros en la entrada se encuentran conectados en serie, en la salida conectados en paralelo, lo cual
conlleva a utiliza los parámetros "h" en la representación de la red de dos puertos del AB y de la RR. Si en la
Figura 3a, utilizamos dicha parámetros obtendremos la Figura 4, y si se trata de encontrar la función de
transferencia X0 / Xs = V0 / Vs, a partir de las leyes de Kirchhoff encontraremos lo siguiente:
Figura 4: Amplificador realimentado utilizando parámetros "h" para representar el AB y la RR
Combinando (9) y (10), y considerando que V0 = V2, obtenemos:
donde
A partir de la ecuación (11) tenemos que
condición que hace que la transmisión de señales hacia adelante sea solamente a través de " a ".
Por otra parte
condición que hace que la transmisión de señales hacia atrás sea solamente a través de " f ".
Para poder escribir las ecuaciones (9) y (10) se debe garantizar en el circuito de la Figura 4 que I1 = I1AB = I1RR ,
y que la corriente que entra al puerto de salida del AB, I2AB, sea igual a la que sale de dicho puerto y la que entra
al puerto de salida de la RR, I2RR. sea igual a la que sale de dicho puerto. Para poder asegurar estas situaciones
se hace uso de las Pruebas de Brune, pruebas mediante las cuales se puede garantizar lo dicho anteriormente y
las cuales se muestran en la Figura 5 para la interconexión de dos redes de dos puertos (AB y RR) conectadas
en serie a la entrada y en paralelo en la salida, tal como es el caso en las Figuras 3a y 4.
Figura 5: Interconexión serie-paralelo y las Pruebas de Brune pertinentes a) Interconexión serie-paralelo
b.1), b.2) Pruebas de Brune y el valor de V = 0 que ha de resultar para que se puedan interconectar AB y
RR sin modificar su estructura
Si en un circuito particular con la interconexión serie paralelo como la mostrada en la Figura 5a se realizan las
pruebas de las Figuras 5b.1 y 5b.2 y se encuentra que V≠0 al menos en un caso, es motivo más que suficiente
para que las ecuaciones (9) y (10) no se puedan sostener y por ende tampoco son valederas las ecuaciones (14) y
(15).
Si rearreglamos la Figura 4 en función de las ecuaciones (14) y (15), obtenemos la Figura 6, de donde se puede
verificar que
como quedó establecido en las ecuaciones (14) y (15).
También a partir de la Figura 6 se puede obtener la impedancia de entrada del circuito "a"
y su admitancia de salida
De donde se puede demostrar que la impedancia de entrada del amplificador realimentado, así como su
admitancia de salida, tienen las siguientes expresiones:
Figura 6: Amplificador realimentado rearreglado
USO Y LIMITACIONES DEL METODO.
CASO 1
Vamos a calcular V0 / VS en el circuito de la Figura 7 utilizando el método descrito en la sección 3.1. Para
utilizar el método descrito lo primero que se debe determinar es si el AB y la RR son redes de dos puertos como
condición necesaria. Efectivamente la Figura 8 determina que el AB y la RR son dos redes de dos puertos, lo,
cual se verifica. Y como condición suficiente, se tiene la prueba de Brune, la cual se aplica en la Figura 9, tal
como se indica en las Figuras 5b.l y 5b.2. Evidentemente en las Figura 9a y 9b se obtiene V = 0 en ambos
casos, lo cual permite hacer uso de los resultados encontrados en las ecuaciones (14) y (15) y los cuales se
llevan a la práctica según la Figura 6 y que se ilustran en la Figura 10.
Figura 7: a) Circuito amplificador completo b) Circuito amplificador para señal. VTh =(Rb / (Rb + RS))VS,
RTh = Rb // RS , Rb = R1 // R2 c) El mismo circuito de b), pero rearreglado para aplicar el método
Figura 8. a) Amplificador básico representado como red de dos puertos. b) Red de realimentación
representada como red de dos puertos.
Figura 9: Aplicación de las Pruebas de Brune a la interconexión serie-paralelo de las redes de dos puertos
la Fig. 8, donde se verifica que V =0.
Figura 10: a) Circuito para la determinación de " a " b) Circuito para la determinación de " f "
Al resolver los circuitos de las Figuras 10a y 10b, e introducir los valores encontrados en la ecuación (8) se
puede demostrar que se obtiene el mismo resultado que al resolver el circuito de la Figura 7b utilizando el
método general de resolución utilizando las leyes de Kirchhoff.
CASO 2.
Nuevamente vamos a calcular V0 / VS en el circuito de la Figura 11 utilizando el método descrito en la sección
3.
Figura 11: Circuito amplificador.
Figura 12: Circuito amplificador rearreglado V's = (Rb / (Rb + RS))VS , R'S = Rb // RS , Rb = R1 // R2
Siguiendo el procedimiento anterior, lo primero a demostrar es que el AB y la RR son redes de dos puertos.
Para ello se muestran en la Figura 13 ambos circuitos, el AB y la RR. Puesto que en la Figura 13a. en el puerto
de entrada y de salida no se cumple que la corriente que entra es igual que la que sale, el AB no es una red de
dos puertos y por consiguiente el método no se puede aplicar. Aún si se obviara este requisito tampoco se
cumplen las Pruebas de Brune tal como se muestra en la Figura 14, donde se puede verificar que en ambos
casos V≠O.
Figura 13: a) Amplificador básico representado como red de dos puertos y donde se verifica que el mismo
no es una red de dos puertos: I1 ≠ I2 ; I3 ≠ I4 b) Red de realimentación representada como red de dos
puertos
Figura 14: Aplicación de las Pruebas de Brune a la interconexión serie-paralelo de las redes dedos
puertos de la Figura 13, donde se verifica que V≠O.
Si aún con estas condiciones se insiste en resolver este problema bajo esta óptica, nosotros vamos a mostrar los
resultados indicando el error cometido cuando se calcula la ganancia de tensión y la resistencia de entrada del
amplificador utilizando el método simplificado a través de sistemas realimentados, con respecto a cuando se
calculan utilizando las leyes de Kirchhoff, que es el método general. Los resultados obtenidos se muestran en
las Figuras 15 y 16, y los mismos fueron calculados a partir del simulador de circuitos PSPICE, sustituyendo
cada transistor por su modelo con parámetros h. En la Figura 15 se muestran los resultados considerando Rc3 =
0.1 KΩ y en la Figura 16 considerando Rc3 = 0.
Figura 15.a: Error en la ganancia en función de 1/ho, y para dos valores de beta de los transistores.
Figura 15.b: Error en la resistencia de entrada en función de 1/ho, y para dos valores de beta de los
transistores.
Figura 16.a: Error en la resistencia de entrada en función de 1/ho, y para dos valores de beta de los
transistores
Figura 16.a: Error en la resistencia de entrada en función de 1/ho, y para dos valores de beta de los
transistores
CONCLUSIONES.
Como se puede notar, el error cometido en el cálculo de la ganancia V0 / VS, utilizando técnicas de
realimentación despreciable cuando el valor de la resistencia de salida de transistores (1/h0 ) del AB es mayor
que 40 KΩ n., lo ci corresponde con los transistores usados comúnmente en circuitos transistorizados.
En cambio, es muy notorio el error de cálculo al usar este método para la determinación de la resistencia de
entrada Ri , del circuito realimentado total, a tal punto que para ha valores de la resistencia de salida de los
transistores el error alcanza hasta un 380 % para transistores con beta = 50 y p valores típicos de h0 el error
puede situarse entre el 20 % y el 100 % para beta comprendido entre 50 y 100, para el circuito mostrado en la
Figura 11.
Estos resultados muestran además que la presencia de Rc3, en el circuito de la Figura 11, hace que el error que
cometa, tanto en la ganancia como en la resistencia de entrada del amplificador realimentado, sea menor.
Finalmente, los resultados demuestran claramente el método de análisis de circuitos realimentados no siempre
es conveniente realizarlo en función del circuito " a " y del circuito " f ", como usualmente lo hacen las personas
relacionadas sistemas de control, pues para ciertos circuitos, tal como el de la Figura 11, existe una flagrante
violación de los principio los cuales se basa el método, lo cual los descarta como posibles candidatos a resolver
a partir de las funciones de transferencia utilizando las técnicas de sistemas realimentados.
REFERENCIAS
1. Gray P. E., Searle C. L., "Principios de Electrónica - Electrónica física, modelos y circuitos
electrónicos", Edit. Reverté, S.A., 1973.
2. Gray P. R., Meyer R. G., "Análisis y Diseño de Circuitos Integrados Analógicos ", Edit. Prentice Hall
Hispanoamericana, S.A., 1993.
3. Guillemin E. A., "Introduccción a la teoría de los circuitos", Edit. Reverté, S.A., 1959.
4. Holt C. A., “Electronics Circuits - Digital and Analog”, Edit. John Wiley & Sons, 1978.
5. Hurst P. J., "Exact Simulation of Feedback Circuit Parameters ", IEEE Trans. on Circuits and Systems,
Vol 38, No. 11, pp. 13821389, noviembre 1991.
6. Ruston & Bordogna, "Electric Networks: Functions, Filters, Analysis ", Edit. Mc Graw Hill, 1966.
7. Sedra S. S., Smith K. C., Microelectronic Circuits ", Saunders College Publishers, 1991.