← ←
Anuncio

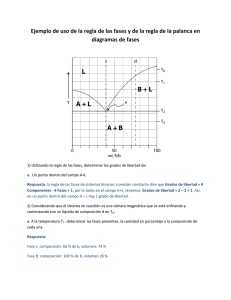
Ciencia de Materiales, 4º curso, 2004/2005 Tema 2. Diagramas de Equilibrio y TTT 2.1. Regla de las fases. 2.2. Diagramas en sistemas binarios. Eutéctico y peritéctico. 2.3. Curvas temperatura-tiempo-transformación. 2.4. Ciencia de Materiales en Internet. 2.1 Regla de las fases. Un diagrama de equilibrio indica las fases presentes en el equilibrio con unas condiciones determinadas. Ya Gibbs en el siglo XIX definió lo que eran fase, componentes y grados de libertad. Fase (F): Es la parte de un sistema que macroscópicamente y microscópicamente es uniforme y homogénea tanto en composición química como en propiedades físicas. Un sistema con una sola fase es homogéneo mientras que con dos o más fases es heterogéneo. El hielo en agua es un sistema heterogéneo porque hay dos fases diferenciadas en propiedades físicas (aunque no en composición), a saber H2O(l) y H2O(s), aunque solo tiene un componente (H2O). Sin embargo, una mezcla de gases es un sistema homogéneo, donde no se pueden distinguir diferentes fases. El aire tiene varios componentes pero es una sola fase. Componente (C): el número de componentes de un sistema es el número mínimo de especies en función de las cuales se puede expresar cuantitativamente la composición de todas las fases. En otras palabras, el número mínimo de especies químicamente independientes para formar las fases. Un balón de vidrio cerrado que contiene las especies PCl5(g), PCl3(g) y Cl2(g) ¿Cuántas fases y componentes contiene? La respuesta sería una fase, ya que todos son gases y por tanto no se pueden separar sino que es una mezcla homogénea en composición y propiedades, y dos componentes. Y es así porque aunque hay tres sustancias químicas no son independientes. Hay un equilibrio químico: PCl3(g) + Cl2(g) ← ⎯⎯⎯⎯⎯→ PCl5(g). Un sistema con CaCO3(s), CaO(s) y CO2(g) es heterogéneo de tres fases (dos sólidas mecánicamente separables y un gas), pero con solo dos componentes ya que los tres compuestos están relacionados mediante la ecuación química: CaCO3(s) ← ⎯⎯⎯⎯⎯→ CaO(s) + CO2(g). Por ejemplo, en el sistema Cu-Zn hay varias fases intermedias: CuZn, Cu5Zn8, CuZn3, pero solo dos componentes (sistema binario) ya que los demás vienen definidos por las reacciones químicas de formación de esos compuestos. En el punto triple del agua coexisten tres fases, es por tanto un sistema heterogéneo. El número de componentes se puede definir como el número total de especies químicas menos el número de reacciones independientes (o de ecuaciones restrictivas en general) del sistema. Grados de libertad (L): es el número de factores externos (P, T, C) de un sistema que pueden cambiarse sin que varie el número de fases del sistema. Si L = 0 se dice que el sistema es invariante. 1 Ciencia de Materiales, 4º curso, 2004/2005 Sistemas con L = 1 se dice que son univariantes o monovariantes. L = 2 son sistemas divariantes y L = 3 sistemas multivariantes. Regla de las fases. F + L = C + 2. A efectos prácticos en un sistema de aleaciones sólidas la temperatura y composición si son parámetros muy importantes y que pueden cambiar pero los cambios en la presión no suelen afectar. Casi todos los cambios son a la misma presión que suele ser la atmosférica. Por tanto en metalurgia se simplifica la regla de las fases a F + L = C + 1 y no se suelen estudiar los efectos de la presión. 2.2. Diagramas en sistemas binarios. Eutéctico y peritéctico. En este caso F + L = 3, ya que el número de componentes es 2 (sistema binario). Los sistemas condensado sólido/líquido se pueden clasificar de varias formas. Una es atendiendo a la miscibilidad entre las fases sólidas y líquidas. Así resulta 8 tipos de diagramas de equilibrio simples (figura 2.1). Los diagramas reales pueden ser así, o más complejos por la unión de diferentes comportamientos en un único sistema. El límite de solubilidad es la cantidad máxima de un componente que se puede disolver en una fase, tanto líquida como sólida. Los diagramas de cambio de estado se constituyen a partir de análisis térmico con gráficas T/t para composiciones conocidas. Primero se calientan los componentes del sistema binario puro y se determinan los puntos de fusión de los dos elementos. En el proceso de solidificación la temperatura es constante (para un elemento puro) o en general para un punto invariante (L=0). Ver figura 2.2. Figura 2.2(a). Grafica T/t (curvas de enfriamiento) Figura 2.2(b). Diagrama de equilibrio Cu-Ni para obtener el diagrama de equilibrio Cu-Ni (solubilidad total, tipo IV) 2 Ciencia de Materiales, 4º curso, 2004/2005 Figura 2.1. Diferentes tipos de diagramas de equilibrio simples sólido-líquido Cuando hay una mezcla de los dos elementos y el comienza a solidificar uno se reconoce en la gráfica por un cambio brusco de pendiente. Llega un momento en que todo solidifica (temperatura constante). Para una de las concentraciones puede permanecer la temperatura constante (eutéctico) como se observa en la figura 2.3 para la curva de enfriamiento de la aleación Pb-Sn. Cuanta más cantidad de masa eutéctica solidifique mayor será el tiempo a la que la mezcla permanezca con la temperatura constante. Para un líquido de composición eutéctica se observa los dos tramos de enfriamiento con un periodo de tiempo a temperatura constante que es máximo. Antes de describir los diferentes tipos de diagramas hay que destacar que no solo son útiles para establecer las fases presentes en unas condiciones determinadas (de composición y temperatura) y para seguir las transformaciones de fase en función de la temperatura o de las 3 Ciencia de Materiales, 4º curso, 2004/2005 composiciones sino que también se emplean para realizar cálculos cuantitativos para determinar que cantidad de cada fase se encuentra en el equilibrio. Para ello se emplea la regla de la palanca. La deducción es la siguiente: sea una composición inicial Co ≈ 55 % a 1250 °C en el diagrama de fases Cu-Ni dado en la figura 2.2(b). En esas condiciones coexisten dos fases, una sólida de composición Cα y otra líquida de composición CL. Se trata de determinar la cantidad de cada una de esas fases que en tanto por uno en peso sería Wα y WL. Para ello sabemos que Wα + WL = 1 (ec. 1) ya que solo hay dos fases y además como las masas de los componentes deben coincidir con la masa total de la aleación: WαCα + WLCL = Co (ec. 2). Combinando ambas ecuaciones se obtiene: WL = (Cα-Co)/(Cα-CL) y Wα = (Co-CL)/(Cα-CL). Conocida como regla de la palanca y fácil de memorizar. Figura 2.3. Gráfica T/t (curvas de enfriamiento) para obtener el diagrama de equilibrio Pb-Sn (solubilidad parcial, tipo V) Tipo I. Diagrama de estado de dos componentes completamente solubles en estado líquido e insolubles en estado sólido. Se conocen como sistemas eutécticos simples. Son el caso típico de las aleaciones Al-Ge, Ge - Zn y Bi - Cd. Las temperaturas de los extremos son los puntos de fusión de los metales A y B, respectivamente. Un dibujo esquemático se presentaba en la figura 2.1. La línea superior se conoce como línea de líquidus. Por encima hay un líquido homogéneo. La línea inferior se conoce como línea de sólidus y por debajo existe un sólido heterogéneo. Sea el punto genérico I, marcado a la izquierda del eutéctico en la figura 2.1 (Tipo I). A la temperatura TI existe un líquido homogéneo de composición aproximada 80 % de A y por tanto 20 % de B. Si se baja la temperatura llega un momento en el que se intersecciona la línea de líquidus. En ese punto comienza a segregarse el sólido A y el líquido se enriquece en B. Se puede seguir bajando la 4 Ciencia de Materiales, 4º curso, 2004/2005 temperatura hasta que se llegue al eutéctico y entonces comenzara a formarse un sólido de composición la propia del eutéctico. En este punto es cuando se segrega B y sigue así hasta que solidifique todo el líquido. Si se comienza con una composición II (derecha del eutéctico) al enfriar y llegar a la línea del líquidus se segrega B y el líquido se concentra en A hasta que se llega a la temperatura del eutéctico en la que comienza a segregarse la composición eutéctica. En el eutéctico la temperatura permanece constante hasta que todo el líquido haya solidificado. El punto E se conoce como eutéctico y es un punto invariante (L=0). Representa la temperatura y composición a la que los sólidos A y B y el líquido están en equilibrio. Por tanto F=3 y al ser un sistema binario C=2 es un punto invariante. En el punto E: 3 + L = 2 + 1 Æ L=0. Tipo II. Diagrama de estado con formación de compuestos de punto de fusión congruentes en aleaciones binarias totalmente miscibles en estado líquido e inmiscibles en estado sólido. Se puede decir que es un caso particular del diagrama anterior donde se forma uno o más compuestos intermetálicos que son compuestos con estequiometría definida y propiedades físicas características y ligeramente diferentes a las de la aleación de los mismos componentes. En la figura 2.1(tipo II) se representa una gráfica típica de este diagrama con la formación de un compuesto intermetálico de estequiometría AB con punto de fusión congruente. Es el caso típico del sistema Cu-Zn, Ag-Sr, o Al-Mg. pF(Al) = 657 °C, pF(Mg) = 650 °C, y pF(Al3Mg4) = 463 °C. En el sistema Ag-Sr donde se forman los compuestos de estequiometría SrAg4, Sr3Ag4, SrAg y Sr3Ag2. En este caso se forma un solo compuesto intermetálico con estequiometría AB y punto de fusión congruente. Se dice que el punto de fusión es congruente cuando un sólido funde dando un líquido de igual composición o alternativamente, un líquido solidifica dando un sólido de la misma composición. Se da la reacción S ← ⎯⎯⎯⎯⎯→ L. Tipo III. Diagrama de estado con formación de compuestos de punto de fusión incongruentes en aleaciones binarias totalmente miscibles en estado líquido e inmiscibles en estado sólido, formando peritécticos. Un ejemplo de este tipo de diagramas se daba en la figura 2.1 (tipo III). Hay compuestos (AB) que tienen puntos de fusión incongruentes: S ← ⎯⎯⎯⎯⎯→ S’ + L, y se denomina reacción peritéctica. Un ejemplo de este tipo de comportamiento es el sistema CaF2 - BeF2. El punto peritéctico (P) es invariante. 3 + L = 2 + 1. Æ L = 0. Un ejemplo de sistema que contiene un eutéctico, un peritéctico y un compuesto con punto de fusión congruente es el sistema Mg-Ni que sa da en la figura 2.4. Existen dos eutécticos: E1 de composición 23 % de Ni y TE ≈ 500 °C [en él cristaliza un líquido para dar dos sólidos de 5 Ciencia de Materiales, 4º curso, 2004/2005 composiciones (α, Mg con un poco de Ni disuelto isomórficamente; y el compuesto intermetálico, Mg2Ni] y E2 de composición 88 % de Ni y TE ≈ 950 °C [en él cristaliza un líquido para dar dos sólidos de composiciones (β, Ni con un poco de Mg disuelto isomórficamente; y el compuesto intermetálico, MgNi2]. Existe un compuesto intermetálico con punto de fusión incongruente (peritéctico) de estequiometría, Mg2Ni y TP ≈ 750 °C. Cuando se calienta este compuesto la reacción de fusión es Mg2Ni (s) Æ LP + MgNi2 (s). Por último, también existe un compuesto intermetálico con punto de fusión congruente de estequiometría, MgNi2 y TF ≈ 1100 °C. Figura 2.4. Diagrama de fases Mg-Ni Tipo IV. Diagrama de estado para aleaciones binarias totalmente miscibles en estado líquido y en estado sólido. No hay líneas horizontales en el diagrama de estado (figura 2.2 (b)), no hay temperatura constante y el rango de composiciones es totalmente variable, y por tanto no hay puntos invariantes además de los puntos de fusión de los componentes extremos. Generalmente ocurre en metales que cristalizan en el mismo tipo de estructura y que tienen un radio atómico similar. P. ej. el sistema Ni-Cu, Pt-Cu, Pd-Cu y Mn-Fe. Se suelen emplear letras griegas para describir las fases sólidas con solubilidad. Partimos de un líquido de composición cualquiera que cuando se enfría y llega a una temperatura T1, se comienza a segregar un sólido de composición variable α. Al seguir enfriando la composición del sólido que se segrega cambia y el líquido se enriquece en el otro elemento. Nunca se pueden encontrar más de dos fases, una líquida y otra sólida por lo que L = 1 (no hay puntos invariantes). En el caso de disoluciones con azeótropos si hay puntos singulares como se vieron en la figura 2.1. Tipo V. Diagrama de estado para aleaciones binarias totalmente miscibles en estado líquido y parcialmente miscibles en estado sólido con la formación de un eutéctico. No hay fases con componentes puros sino que las fases son disoluciones sólidas. Un caso típico es el sistema Ag-Cu o Pb-Sn que se utiliza en las barras de soldadura (figura 2.5). Existe una solubilidad parcial (pequeña y variable con T) del Sn en el Pb (fase α) y también del Pb en el Sn (fase β). La existencia 6 Ciencia de Materiales, 4º curso, 2004/2005 de las fases sólidas α y β viene definida por la línea de solvus que da la solubilidad máxima de un componente en el otro para una temperatura determinada. En el punto de composición eutéctica (61.9 % de Sn y 183 °C) se da la reacción: L ← ⎯⎯⎯⎯⎯→ α + β. Figura 2.5. Diagrama de fases Pb-Sn Se pueden distinguir dos líquidos de composición inicial (19.2 % Pb > cI > cE) y otro con (0 > cI > 19.2 % Pb). En el primer caso, al enfriar un líquido de composición genérica se llega a un punto donde se segrega un sólido α (Pb con algo de Sn), obviamente el líquido se va concentrado en Sn. Al seguir enfriando se obtiene más fase α y líquido de composición variable hasta que se llega al eutéctico (punto invariante, L = 0, ya que coexisten tres fases (α, β y el líquido)) por lo que la temperatura no cambia hasta que solidifica todo el líquido. Por tanto, al final se obtiene una mezcla de fases de composición α y la composición del eutéctico α+β. La microestructura de la muestra consiste en partícula de composición α (denominado proeutéctico, “antes del eutéctico”) y partículas de la composición del eutéctico que contiene las fases α y β en la relación estequiométrica que dicta el eutéctico y con una microestructura característica y que depende del sistema en estudio. En el segundo caso (0 > cI > 19.2 % Pb), al enfriar un líquido de composición genérica se llega a un punto donde se segrega un sólido α, obviamente el líquido se va concentrado en Sn, hasta que solidifica todo el líquido para dar solo fase α. Después, al bajar en temperatura se puede 7 Ciencia de Materiales, 4º curso, 2004/2005 sobrepasar el límite de solubilidad y se segrega fase β del sólido α. En este caso no hay punto invariante y por tanto no hay una temperatura constante. Tipo VI. Diagrama de estado para aleaciones binarias totalmente miscibles en estado líquido y parcialmente miscibles en estado sólido con la formación de un peritéctico. Un caso típico puede ser el sistema Pt-W y el diagrama de fases se dio en la figura 2.1 (tipo VI). La reacción peritéctica puede ser que al elevar la temperatura α ← ⎯⎯⎯⎯⎯→ L + β, o bien, β ← ⎯⎯⎯⎯⎯→ L + α. La transformación es un punto invariante donde T es constante hasta que no se consuma una de las fases. La fase α es Pt con W y β W con Pt. Tipo VII. Diagrama de estado para aleaciones binarias parcialmente miscibles en estado líquido e inmiscibles en estado sólido. Un caso típico es el sistema Mn-Ce. El diagrama de estado esquemático se dio en la figura 2.1 (tipo VII). La única novedad es una zona donde coexisten dos líquidos inmiscibles. Tipo VIII. Diagrama de estado para sistemas binarios inmiscibles tanto en estado líquido como en estado sólido. No hay aleaciones de ninguna clase. Ni en estado sólido ni en estado líquido. Un diagrama típico se dio en la figura 2.1 (tipo VIII). Es el caso del sistema V-Ag. En estado líquido están separados por las densidades y para cualquier composición, al enfriar se produce segregación de las dos fases sólidas. TF(V)=1890 °C, ρ(V)=6.0 g/cc, TF(Ag) =960 °C, ρ(Ag)=10.5 g/cc. Eutectoide se define como un punto invariante en una reacción en estado sólido (entre fases sólidas) La reacción en enfriamiento sería: α Æ β + γ. Se dice que es una cristalización secundaria. Peritectoide es similar, es un punto invariante en una reacción en estado sólido entre fases de diferente composición. La reacción en enfriamiento sería: α + β Æ γ. Los diagramas reales son bastante complejos (como se ha visto en algún caso) ya que pueden ser una mezcla de varios de los tipos que hemos estudiado por separado. Como ejemplo de esta complejidad se da el diagrama de fases del sistema cerámico Al2O3SiO2 que contiene mullita como una fase sólida intermedia (fase de estequiometría ligeramente variable entorno al valor medio 3Al2O3.2SiO2. Se muestran las composiciones típica de los refractarios (materiales resistentes a temperaturas muy altas) más comunes así como la fotografías bajo el microscopio electrónico que indica la microestructura más común de estas fases. 2.3. Curvas temperatura-tiempo-transformación (TTT). Son diagramas donde se describen los procesos de transformaciones de fase en función de dos variables, la temperatura y el tiempo. Diagramas TTT: temperatura, tiempo y transformación. En el caso particular de los aceros 8 Ciencia de Materiales, 4º curso, 2004/2005 se trata de determinar las transformaciones de fase de la austenita en función de la temperatura y el tiempo. Las transformaciones pueden ser isotermas o por enfriamiento continuo. Generalmente se trabaja con los diagramas de transformación isotérmica. Figura 2.6. Diagrama de fases del sistema cerámico Al2O3-SiO2 Es importante destacar que en los diagramas TTT aparecen fases metaestables que no aparecen en los diagramas de equilibrio. Por ejemplo, en el sistema SiO2, hay varias fases polimórficas (cuarzo, tridimita y cristobalita) Además, al enfriar rápidamente la tridimita no cambia a cuarzo sino a la fase tridimita de baja temperatura. Esta fase es metaestable y no aparece en el diagrama de fases (la estable en esas condiciones es el cuarzo de baja temperatura) pero si se enfría rápidamente es metaestable por mucho tiempo. Otro ejemplo de fase metaestable es la martensita que se obtiene al enfriar los aceros austeníticos muy rápidamente. A temperatura ambiente las fases estables que se observan experimentalmente son ferrita y cementita con microestructura perlítica (termodinámicamente: ferrita y grafito). Se pueden determinar dos tipos de transformaciones de gran importancia: a) Transformaciones con difusión atómica (caracterizadas por cinéticas lentas); y b) Transformaciones 9 Ciencia de Materiales, 4º curso, 2004/2005 sin difusión (martensíticas) solo hay distorsiones. En los diagramas TTT aparecen los dos tipos de transformaciones aunque solo una resulte en la fase estable a temperatura ambiente. Para obtener los diagramas TTT se opera de la forma siguiente: 1.- El conjunto de probetas de la aleación de la misma composición, bajo estudio, se calientan y se mantienen a temperatura constante (en el caso de los aceros hasta austenización total). 2.- A continuación se enfrían bruscamente hasta la temperatura determinada sumergiendo la probeta en un baño de sales fundidas de tal forma que la temperatura se mantenga constante. 3.- A intervalos de tiempo controlados se sacan las probetas para seguir las transformaciones de fases, y microestructuras presentes, principalmente con la ayuda del microscopio metalográfico y DRX. 4.- Se representan los resultados de las transformaciones de fase (en condiciones de no equilibrio) en los diagramas TTT (figura 2.7). Para ello, de cada experimento a una temperatura constante conocida se extraen tres puntos (tiempos) que corresponden al inicio de la transformación (> 1 %) al punto intermedio (50 %) y al punto final (> 99 %). Pueden haber varios tipos de transformaciones (no solo un eutéctico) con lo que los diagramas TTT se pueden complicar mucho. Aunque depende de las composiciones, la transformación de la austenita a las diferentes fases o microestructuras tienen lugar en rangos de temperatura determinados. La transformación de la austenita depende principalmente de la velocidad de enfriamiento. T > 725 °C, austenita; 725 > T > 500, perlita fina; 500 > T > 225, bainita; 225 > T, martensita. Ms es la temperatura a la que comienza a formarse la martensita y Mf es la temperatura a la que termina de formarse la martensita. Estas temperaturas cambian dependiendo de la composición del acero. Si % C aumenta Ms disminuye. % C = 0.7 Æ Ms = 300 °C. % C = 1.1 Æ Ms = 200 °C. % C = 1.6 Æ Ms = 100 °C. 10 Ciencia de Materiales, 4º curso, 2004/2005 Figura 2.7. Obtención de un diagrama de transformación isotérmica (abajo) a partir del porcentaje de transformación en función del tiempo de experimentación (acero genérico) 2.4. Ciencia de Materiales en Internet. Buscadores. (P. ej. Google, en http://www.google.es/ ) Sociedades científicas. ACS en http://www.acs.org ; MRS en http://www.mrs.org/ Venta de libros. (P. ej. http://www.amazon.com/ ) Empresas. (p. ej. ACERINOX en http://www.acerinox.es/ con un esquema muy claro del proceso de producción de acero inoxidable) Una web muy buena donde hay mucha información sobre cursos de materiales es la: MITOPENCOURSEWARE: que es la web del Massachussets Institute of Technology. http://ocw.mit.edu/ En esta web hay muchos cursos “on-line” y se pueden elegir aquellos dedicados a ciencia de los materiales: Materials Science and Engineering. Por ejemplo el curso dedicado a “Electrical, Optical & Magnetic Materials and Devices, Fall 2003” hay un tema dedicado a materiales para almacenamiento de información. 11