centro de gravedad - Tusclasesparticulares

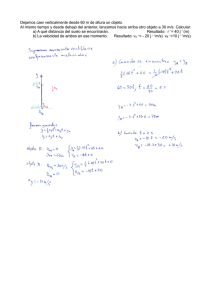
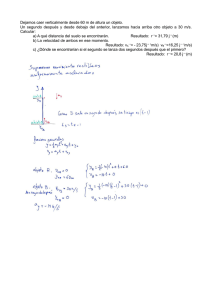
CENTRO DE GRAVEDAD
¿Por qué, si nos inclinamos hacia adelante, llega un momento en que perdemos el
equilibrio y nos caemos?. ¿Por qué no se cae la Torre de Pisa? El centro de gravedad es
un concepto que se utiliza para estudiar la estabilidad de los objetos, y de él tratamos en
este post.
Torre de Pisa
Supongamos que rompemos un dado en miles de trocitos. Si dejamos caer cada uno de
dichos trocitos, la tierra lo atraerá y lo hará caer al suelo. Dado que son minúsculos,
decimos que el centro de gravedad de cada uno de ellos es el propio trocito. Pero ¿qué
ocurre con el dado? Si lo dejamos caer, ¿cómo lo atrae la tierra?. Para solucionar este
problema se recurre a un concepto virtual e inexistente; se suman las masas de todos los
trocitos (que es la masa total del dado) y se supone que toda ella está concentrada en un
solo punto, al cual llamamos “centro de gravedad del dado”. ¿Por qué hacemos esto? para
poder tener un convenio acerca de cómo estudiar el equilibrio de los cuerpos.
Importante: el centro de gravedad no existe físicamente sino que es un
convenio. Se trata del punto donde suponemos que está concentrada
toda la masa de un cuerpo.
En este post únicamente trataremos los centros de gravedad de los cuerpos simétricos. El
cuerpo de gravedad de un cuerpo simétrico se halla en su centro de geometría.
En las figuras siguientes vemos ejemplos de los centros de gravedad de distintos cuerpos
simétricos (recordemos que la masa del cuerpo está distribuida por todo el cuerpo y que el
centro de gravedad, situado en su centro geométrico, es un convenio). Como podemos
apreciar, en todos ellos el centro de gravedad se sitúa en el centro geométrico del cuerpo.
Y ahora vamos a hablar de equilibrio. Para que un objeto cualquiera colocado
verticalmente no se vuelque, es necesario que la vertical que pasa por su centro de
gravedad no se salga fuera de la base de dicho objeto.
En la figura siguiente vemos que al pasar de la posición 1 a la posición 2, si trazamos una
línea vertical, llegamos todavía al espacio ocupado por la base; pero al pasar a la posición
3 y dibujar una línea vertical, ésta ya queda fuera de la base del objeto y, por tanto, el
cuerpo se desequilibra y cae.
Veamos ahora el caso de un cilindro inclinado. Seguro que todos habéis adivinado que el
cilindro de a continuación es inestable, y que se caerá. ¿Verdad que si hubiéramos
diseñado la base más ancha, entonces sí que se aguantaría?
Las llamadas torres inclinadas de Pisa, Bolonia o Arcángel no se caen, a pesar de su
inclinación, porque la vertical de sus centros de gravedad no rebasa los límites de sus
bases (otro motivo, pero de segundo orden, es la profundidad a que sus cimientos se
hunden en tierra).
Torres inclinadas de Bolonia