x - Cenidet

S.E.P.
S.E.I.T.
D.G.I.T.
CENTRO NACIONAL DE INVESTIGACIÓN Y
DESARROLLO TECNOLÓGICO
cenidet
CONTROL VECTORIAL DE UN MOTOR DE
INDUCCIÓN DOBLE ALIMENTADO (MIDA)
T
E
S
I
S
QUE PARA OBTENER EL GRADO DE
MAESTRO EN CIENCIAS
EN INGENIERÍA ELECTRÓNICA
PRESENTA
ING. MIRIAM CUEVAS CUEVAS
DIRECTORES DE TESIS:
M.C. PATRICIA CARATOZZOLO MARTELLITI
Dr. GERARDO VICENTE GUERRERO RAMÍREZ
CUERNAVACA, MOR.
JUNIO, 2003
DEDICATORIA
A Dios y
A mis padres
Josefa y Gonzalo
Gracias por su amor infinito y
su apoyo incondicional
Los AMO
AGRADECIMIENTOS
1- A mis directores de tesis, M.C. Patricia Caratozzolo Martelliti y al Dr.
Gerardo V. Guerrero Ramírez, por el apoyo brindado para la realización
del trabajo.
2- A mis revisores, Dr. Luis Gerardo Vela Valdés, Dr. Alejandro Rodríguez
Palacios y al Dr. Marco Antonio Oliver Salazar, por sus acertados
consejos en el desarrollo de este trabajo.
3- A todos mis profesores por compartir sus valiosos conocimientos conmigo.
4- A mi tía Anita, por apoyarme y defender mis ideales.
5- A la dirección, planta docente y personal en general del Centro Nacional
de Investigación y Desarrollo Tecnológico (CENIDET).
6- Al Consejo del Sistema Nacional de Educación Tecnológica (Cosnet) y a la
Secretaría de Educación Pública (SEP), a través de la cual, mediante sus
convenios académicos, tuve la oportunidad de recibir el apoyo de una beca
económica para cursar los estudios de maestría.
7- A mis amigos por ser tan incondicionales en su amistad y apoyo.
8- A todas las personas, que de una forma u otra me brindaron su apoyo
durante todo este tiempo. Gracias.
ÍNDICE
ÍNDICE
LISTA DE FIGURAS
LISTA DE TABLAS
SIMBOLOGÍA
I
III
VI
VII
CAPÍTULO 1: Introducción
1. 1:
1. 2:
1. 3:
1. 4:
1
Justificación, alcances y aportaciones del trabajo de tesis
Estado del arte
Organización del trabajo de tesis
Resultados del trabajo de tesis
CAPÍTULO 2: Generalidades sobre el motor de inducción de rotor
devanado (MIRD) y su uso como motor de inducción doble
alimentado (MIDA).
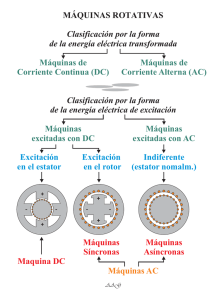
2. 1: Clasificación de los motores eléctricos
2. 2: Principios de funcionamiento del motor de inducción
2.2. 1: Ecuaciones físicas
2.2. 2: Ecuaciones de voltaje
2.2. 3: Ecuación del par
2
3
5
5
7
7
9
11
12
14
2. 3: Introducción a la teoría de marcos de referencia (MR)
15
2.3. 1: Modelo de la máquina de inducción en el MR Arbitrario
17
2. 4: Ecuaciones del modelo bifásico del MIDA
2.4. 1: Ecuaciones del MIDA en un MRA
2.4. 2: Ecuaciones del MIDA en un MRF al estator
2. 5: Circuito equivalente del Motor de Inducción
CAPÍTULO 3: Motor de inducción doble alimentado
3. 1: Flujo de potencias y pérdidas en el estator y rotor.
3. 2: Análisis del MIDA en estado estacionario
3. 3: Modelado del MIDA en lazo abierto en un MRF
I
18
22
23
24
27
27
31
42
CAPÍTULO 4: Estrategias de control de la máquina de inducción de
rotor devanado (MIRD)
4. 1: Métodos clásicos de control del MIRD
4.1. 1: Formas de control de velocidad del MIRD
4.1. 2: Recuperación de potencia en un MIRD
4. 2: Introducción al control vectorial
4. 3: Transformaciones de MR orientados según flujo
4.3. 1: Marco de referencia orientado al flujo del rotor
4.3. 2: Marco de referencia orientado al flujo del estator
4.3. 3: Marco de referencia orientado al flujo de magnetización
4. 4: Fundamentos de la implementación del control vectorial
4. 5: Método directo e indirecto de control por campo orientado
CAPÍTULO 5: Control vectorial aplicado al MIDA
5. 1: FOC del motor de inducción doble alimentado
Ecuaciones del control en un marco de referencia orientado al
5.1. 1:
flujo del estator.
5.1. 2: Condiciones del control de campo orientado (FOC)
5. 2: Diagrama en bloques de la estrategia de control
53
53
53
56
57
59
61
64
66
67
68
73
73
74
78
80
Esquema general del control orientado al flujo del estator
aplicado al MIDA
81
5. 3: Resultados de simulación obtenidos al aplicarle el FOC al
MIDA
85
5.2. 1:
CONCLUSIONES
93
REFERENCIAS Y BIBLIOGRAFÍA
99
Referencias
Bibliografía adicional consultada
ANEXOS.
Anexo 1:
Anexo 2:
Listado del programa en MATLAB.
Librerías desarrolladas en Simulink/MATLAB
II
99
101
103
106
LISTA DE FIGURAS
Figura 2- 1
Figura 2- 2
Figura 2- 3
Figura 2- 4
Figura 2- 5
Figura 2- 6
Clasificación de los motores eléctricos.
Motor de inducción de rotor devanado.
Principio de operación del motor de inducción.
Configuración física de una MIDA.
Diagrama esquemático del motor de inducción trifásico.
Diagrama eléctrico de los devanados del estator y rotor del
motor de inducción trifásico.
Figura 2- 7 Relación entre las variables trifásicas (abc) y bifásicas (dq0).
Figura 2- 8 Relación entre las variables trifásicas y bifásicas en un MRA.
Figura 2- 9 Circuito equivalente por fase de un motor de inducción.
Figura 3- 1 Diagrama del flujo de potencias en un motor de inducción.
Figura 3- 2 Flujo de potencias en modo Motor del MIDA. a) y b) operación a
velocidad sub-síncrona.
Figura 3- 3 Flujo de potencias en modo motor. a) y b) operación a velocidad
super-síncrona.
Figura 3- 4 Modo generador. a) y b) operación a velocidad sub-síncrona.
Figura 3- 5 Modo generador. a) y b) operación a velocidad super-síncrona.
Figura 3- 6 Circuito equivalente por fase del MIDA.
Figura 3- 7 Curva característica Par ( τ s ) & deslizamiento.
Figura 3- 8 Curva característica Par ( τ r ) & deslizamiento.
Figura 3- 9 Curva característica Par ( τ sr ) & deslizamiento.
Figura 3- 10 Curva característica Par total ( τ T ) & deslizamiento.
Figura 3- 11 Diagrama esquemático del MIDA en lazo abierto.
Figura 3- 12 Voltajes de alimentación ( v as , v bs , v cs ) & tiempo en segundos.
Figura 3- 13 Voltajes v qs , v ds del estator & tiempo.
Página
8
9
9
10
11
12
16
17
24
28
29
29
30
30
31
39
40
40
41
42
43
44
Figura 3- 14 Voltajes v ar , v br , v cr & tiempo.
Figura 3- 15 Voltajes v qr , v dr & tiempo.
46
Figura 3- 16 Corrientes i , i del estator & tiempo.
qs ds
47
Figura 3- 17 Corrientes i qr , i dr del rotor & tiempo.
47
Figura 3- 18 Corrientes trifásicas el estator.
48
Figura 3- 19 Corrientes trifásicas del rotor.
Figura 3- 20 Velocidad mecánica y posición del rotor.
Figura 3- 21 Par electromagnético
48
49
41
46
III
LISTA DE FIGURAS
Figura 4- 1 Motor de inducción de rotor devanado y resistencias adicionales
en el rotor .
Figura 4- 2 Esquemático de los devanados del MIRD con resistencias
externas.
Figura 4- 3 Variación de velocidad en un MIRD con resistencia variable en
el rotor.
Figura 4- 4 Control de velocidad de un MIRD usando un resistor de carga y
un chopper.
Figura 4- 5 Control de velocidad usando una batería de voltaje variable.
Figura 4- 6 Control de velocidad usando un rectificador y un inversor
conmutado naturalmente.
Figura 4- 7 Analogía entre el motor de cd y el control vectorial del motor de
inducción.
Figura 4- 8 Marco de referencia general.
Figura 4- 9 Marco de referencia orientado al flujo del rotor (x,y).
Figura 4- 10 Fasor del flujo rotórico.
Figura 4- 11 Transformación de las variables en el MR ‘D,Q’ a variables en el
MR ‘x,y’.
Figura 4- 12 Componentes en cuadratura según el marco de referencia
orientado al flujo del rotor.
Figura 4- 13 Componentes de corriente que producen el par.
Figura 4- 14 Componentes en cuadratura según el marco de referencia
orientado al flujo del estator.
Figura 4- 15 Componentes de corriente que producen el par.
Figura 4- 16 Marco de referencia orientado al flujo de magnetización.
Figura 4- 17 Componentes en cuadratura según el marco de referencia
orientado al flujo de magnetización.
Figura 4- 18 transformación de planos de coordenadas.
Figura 4- 19 Diagrama de las corrientes (directa y en cuadratura) orientadas a
los distintos marcos de referencia.
Figura 5- 1
Figura 5- 2
Figura 5- 3
Figura 5- 4
Figura 5- 5
Figura 5- 6
Figura 5- 7
Configuración física de una MIDA.
Marco de referencia general.
Diagrama esquemático del FOC aplicado al MIDA.
Sistema de referencia en el marco de referencia natural.
Esquemático del control orientado al flujo estatórico del MIDA.
Módulo de la corriente de magnetización del estator.
Ángulo ρ s de la corriente de magnetización.
Figura 5- 8 Componentes del fasor de la corriente del estator en un marco
de referencia orientado al flujo del estator.
Figura 5- 9 Componentes del fasor de la corriente del rotor en un marco de
referencia orientado al flujo del estator.
Figura 5- 10 Voltajes del rotor
IV
54
54
55
55
56
57
58
60
61
61
62
63
64
65
66
66
67
68
70
74
78
80
80
83
86
86
87
87
88
LISTA DE FIGURAS
Figura 5- 11 Ensayo 1, velocidad de referencia ( ω ref ) & velocidad mecánica
del rotor ( ω rm ).
Figura 5- 12 Ensayo 1, Par electromagnético en N-m.
Figura 5- 13 Ensayo 2, velocidad de referencia ( ω ref ) & velocidad mecánica
del rotor ( ω rm )
Figura 5- 14 Ensayo 2, Par electromagnético en N-m.
V
89
89
90
90
LISTA DE TABLAS
LISTA DE TABLAS
Tabla 2- 1
Marcos de referencia
18
Tabla 3- 1
Tabla 3- 2
Tabla 3- 3
Velocidades sub-síncrona y super-síncrona.
Formulas de potencias y pérdidas en un motor de inducción.
Parámetros del MIDA..
30
32
43
Tabla 5- 1
Parámetros del MIDA..
85
VI
SIMBOLOGÍA
Ns
Número de vueltas en los devanados del estator.
Nr
Número de vueltas en los devanados del rotor.
Rs
Resistencia de los devanados del estator.
Rr
s
r
Resistencia de los devanados del rotor.
Denota las variables y parámetros asociados al estator.
Denota las variables y parámetros asociados al rotor.
v as , v bs , v cs Voltajes en las fases a, b, c del estator.
v ar , v br , v cr Voltajes en las fases a, b, c del rotor.
i as , i bs , i cs
Corrientes en las fases a, b, c del estator.
i ar , i br , i cr
Corrientes en las fases a, b, c del rotor.
λ as , λ bs , λ cs Enlaces de flujo en las fases a, b, c del estator.
λ as , λ bs , λ cs Enlaces de flujo en las fases a, b, c del rotor.
v sabc
Voltajes trifásicos del estator.
r
v abc
Voltajes trifásicos del rotor.
i sabc
Corrientes trifásicas del estator.
r
i abc
Corriente trifásica del rotor.
λsabc
Enlaces de flujo trifásicos del estator.
λrabc
ρ
Enlaces de flujo trifásicos del rotor.
L ls
L lr
L ms
L mr
Inductancia de dispersión de los devanados de estator.
Operador de derivación, d
dt
.
Inductancia de dispersión de los devanados de rotor.
Inductancia de magnetización de los devanados de estator.
Inductancia de magnetización de los devanados de rotor.
Lm
Inductancia de magnetización.
L sr
Inductancia de mutua entre los devanados de estator y rotor.
L ls + L ms
L lr + L mr
θr
Inductancia propia de los devanados de estator.
Inductancia propia de los devanados de rotor.
Posición angular del rotor.
VII
SIMBOLOGÍA
µ0
Constante de permeabilidad (µ0=546565665).
r
Radio a la mitad del entrehierro.
l
Longitud axial del entrehierro.
g
Longitud uniforme del entrehierro.
Np
Número de pares de polos.
τem
Par electromagnético.
ωr
J
β
τL
f
Velocidad angular del rotor.
Inercia del rotor y de la carga (Kg.m2).
Coeficiente de fricción viscosa.
Par de carga
Representa cualquier sistema 3φ de variables eléctricas (voltajes,
corrientes, pares, etc.).
es el conjunto de valores reales admisibles para las variables físicas
involucradas,
Ω
abc
qd0
θq
Tqd0(θq)
MRA
Sistema de variables originales.
Sistema de variables resultantes.
Ángulo entre el eje q y el eje d, girando a velocidad ωr.
Matriz de transformación.
Marco de Referencia Arbitraria.
MR
Marco de referencia.
Pin
Potencia de entrada instantánea.
MRF
Marco de Referencia Fijo.
r1
Resistencia por fase del estator.
r2
Resistencia por fase del rotor.
rm
Resistencia por pérdidas de excitación (o del núcleo).
X1
Reactancia de dispersión del devanado del estator,
X2
Reactancia de dispersión del devanado del rotor,
Xf
ψ
Reactancia de magnetización.
λ
Pe
Enlaces de flujo total (sistemas en general).
Enlaces de flujo (Sistemas lineales).
Potencia eléctrica de entrada.
Pjs
Pérdidas por el cobre del estator.
Pnc
Pérdidas en el núcleo.
Pg
Potencia en el entrehierro.
Pjr
Pérdidas por el cobre del rotor.
Pm
Potencia mecánica.
Pv
Pérdidas por fricción.
PL
Potencia mecánica total.
Ps
Es la potencia entregada al entrehierro desde el estator
VIII
SIMBOLOGÍA
Pr
Es la potencia entregada al entrehierro del lado del rotor
s
Deslizamiento
Fasor de la corriente del estator.
→
I1
→
Fasor de la corriente del rotor.
→
Fasor del voltaje del estator.
→
Fasor del voltaje del rotor.
I2
v1
v2
a
P1
Q1
Pr1
Q X1
Ángulo al que desfasará el voltaje del rotor.
Potencia activa de entrada de la fuente al estator.
Potencia reactiva del estator.
Pérdidas en la resistencia de los devanados del estator.
Potencia reactiva en la reactancia de fuga X 1 del estator.
Q Xf
Potencia reactiva en la reactancia de magnetización ( X f ).
Pg1
Potencia activa del entrehierro desde el estator.
Q g1
Potencia reactiva del entrehierro desde el estator.
P2
Potencia activa entregada al del rotor por la fuente de excitación en el
rotor.
Q2
Pr 2
Q X2
Potencia reactiva entregada al rotor por la fuente de excitación en el rotor
Pg 2
Potencia activa del entrehierro entregada desde el rotor.
Qg2
Potencia reactiva del entrehierro entregada desde el rotor.
“ 2b ”
“ 2b ”
ωs
Pérdidas en la resistencia del rotor.
Potencia reactiva en la reactancia de fuga ( X 2 ).
Indica que el motor se encuentra en operación sub-síncrona.
El número “2”, indica que es una variable del rotor y “b” que está en
operación sub-síncrona.
Indica que el sistema se encuentra en operación super-síncrona.
Velocidad síncrona .
Pm
Potencia mecánica en Watts.
τr
Par asíncrono constante para un deslizamiento dado, producido por el
voltaje v1 suministrado al estator.
Par asíncrono constante para un deslizamiento dado, producido por el
voltaje v 2 aplicado al rotor.
Par producido por la interacción de los campos del estator y rotor.
τs
τ sr
τT
El par total es la suma de los tres pares ( τ T = τ1 + τ 2 + τ s ).
VP
Voltaje pico de alimentación por fase.
θi
Posición inicial del rotor.
ωr
Velocidad eléctrica del rotor en rad/seg.
fr
Frecuencia en el rotor.
IX
SIMBOLOGÍA
fs
ηsin c
Velocidad síncrona ó velocidad del campo magnético en rpm.
ηm
Velocidad mecánica del eje del rotor en rpm.
Rd
Resistencia aparente.
D
Ciclo de trabajo del chopper.
Eoc
E2
Voltaje del rotor a circuito abierto.
Voltaje de corriente directa dado por el inversor.
ET
Voltaje del devanado secundario del transformador.
Ia
Corriente de armadura.
If
Corriente para el devanado de campo.
Kt
Constante de proporcionalidad.
(x , y )
Componentes en un marco de referencia general.
ψ sg
Fasor de flujo general.
ωg
Velocidad general
sD , sQ
rα , rβ
'
ψr
(x , y )
(i
Frecuencia síncrona.
x
,iy )
→
| ψr |
Componentes o fases del estator.
Componentes o fases del rotor.
Fasor del flujo del rotor.
Componentes o fases del marco de referencia orientado al flujo del rotor,
estator o de magnetización.
Componentes del fasor de corriente del estator orientadas a marco de
referencia del rotor, estator o de magnetización.
Magnitud del flujo del rotor.
ρr
Ángulo del flujo del rotor.
→'
Fasor del flujo del estator.
ψs
ω ms
Velocidad del flujo del estator.
X
CAPÍTULO 1
INTRODUCCIÓN
El control de velocidad de motores de corriente alterna (ca) de tipo inducción ha adquirido
gran auge en los últimos años debido a las ventajas de este tipo de motores y al desarrollo
alcanzado en la tecnología de los convertidores electrónicos de potencia (inversores,
convertidores cd/cd, cicloconvertidores) y los microprocesadores. Asimismo, la
posibilidad de implementar los complejos algoritmos necesarios en el control de este tipo
de máquinas, permite enfrentar los problemas de control de motores de inducción muy
difíciles de llevar a la práctica años atrás.
Aún con las ventajas como: bajo costo, alta fiabilidad, robustez, etc, la máquina de
inducción posee características problemáticas en lo que respecta al control, las cuales son:
•
Dificultad en el control, puesto que es un sistema no lineal, multivariable y
acoplado.
•
Variaciones considerables en la resistencia rotórica que modifican el
comportamiento del sistema.
•
Sistema variante en el tiempo.
A partir de los años 70’s estos problemas fueron solucionados con la introducción del
Control por Campo Orientado (FOC: field oriented control) [3]. Posteriormente se
adaptaron para el control de motores eléctricos otras técnicas de control no lineales como
son: Control deslizante, Control de sistemas linealizados, Control adaptable, Control robusto y
otros; logrando así, no solo resolver los problemas antes mencionados sino además logran
excelentes resultados en seguimiento de trayectoria (velocidad, posición y par).
La técnica de control vectorial o control por campo orientado, FOC [2], se ideó para el
control de la máquina síncrona. Sin embargo, actualmente también se aplica a los motores
de inducción; que ofrece entre, otras ventajas, el desacoplamiento de las variables del
motor. Además, permite un control independiente de velocidad y par equiparables a la
sencillez en el motor de corriente directa de excitación separada y mejora la respuesta
dinámica y la precisión con respecto al control escalar [13]. Ello abre la posibilidad del
empleo de motores de inducción baratos y de muy bajo mantenimiento en aplicaciones
que tradicionalmente han estado reservadas a motores de corriente directa (cd) [4].
1
Capítulo 1
Introducción
La aplicación del FOC en los motores de inducción es un tema reportado continuamente
en la literatura especializada. Es un hecho que los laboratorios y centros de investigación
dedicados al desarrollo de sistemas de control de motores, deben poseer la infraestructura
tecnológica necesaria para asumir los retos de investigación y docencia en este campo.
1.1 Justificación, alcances y aportaciones del trabajo de tesis
Justificación del trabajo de tesis
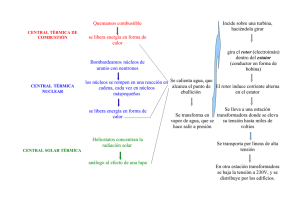
En la industria, aproximadamente la mitad de la electricidad consumida se debe a las
bombas, ventiladores, equipos de aire acondicionado, etc. y no toda la potencia eléctrica
convertida en potencia mecánica se aprovecha; generalmente una gran parte se pierde en
forma de calor. Con la máquina de inducción de rotor devanado en configuración doble
alimentado se pretende recuperar la mayor parte de la energía que se desecha en forma de
calor.
El esquema del motor de inducción doble alimentado (MIDA) resulta muy atractivo para
aquellas aplicaciones donde el intervalo de velocidad es limitado y donde la recuperación de
energía es un factor dominante. Se aprovecha una de las ventajas sobresalientes que
presentan el MIDA, la cual consiste en posibilitar el control, en forma desacoplada, de las
potencias activas y reactivas generadas o absorbidas, apoyándose para esto en técnicas de
Control Vectorial o Campo Orientado.
La escasa cantidad de publicaciones sobre el MIDA en modo motor motivó el interés en
este trabajo de tesis, especialmente teniendo en cuenta:
1. La necesidad del desarrollo de un modelo matemático general
basándose en la técnica de Control Vectorial.
de un MIDA
2. La necesidad de asimilación de una tecnología de punta en el campo del control de
motores y en general de la electrónica de potencia.
Alcances del trabajo de tesis
El alcance del trabajo de tesis consiste en el desarrollo de un esquema de control de
regulación de velocidad para un motor de inducción doble alimentado (MIDA), mediante
técnicas de control vectorial. Las metas que se pretenden alcanzar son:
•
El modelo matemático y análisis en estado estacionario del motor de inducción de
rotor devanado en configuración doble alimentado.
•
El análisis del flujo de potencias del MIDA.
•
La simulación digital del MIDA en lazo abierto, utilizando la herramienta
“Simulink” de Matlab.
2
Capítulo 1
Introducción
•
Diseño de un sistema de control de la velocidad de un MIDA basado en el control
vectorial.
•
Simulación del control de velocidad del motor de inducción doble alimentado,
utilizando la herramienta de MATLAB/ Simulink.
Aportación del trabajo de tesis
Este trabajo está enmarcado en un proyecto de la línea de investigación de máquinas
eléctricas del área de Control No Lineal del CENIDET, encaminado al diseño de un control
vectorial de la velocidad de un motor de inducción doble alimentado (MIDA), con el
objetivo de estudiar el flujo de potencias.
Mediante el análisis en estado estacionario, el análisis del flujo de potencias y la
simulación del control de velocidad de un MIDA aplicando la técnica del control de
campo orientado se contribuirá a fortalecer la Línea de Investigación de máquinas eléctricas
iniciado desde hace unos años en este centro.
1.2 Estado del arte
Marco conceptual y revisión del estado del arte
En esta sección se hace referencia a algunas soluciones dadas en el área del control de
máquinas de inducción en los últimos años. Las fuentes bibliográficas fundamentales que
sirven de base en la realización de este trabajo, son las siguientes:
1- Publicaciones en revistas y congresos, en especial las del IEEE/IAS las cuales reportan lo
más novedoso en esta temática, presentados en los eventos internacionales más
relevantes de esta organización.
2- Página WEB de fabricantes de motores y de control vectorial por ejemplo la página WEB de
Texas Instruments (www.ti.com), en la cual se pueden encontrar tanto los manuales de
usuario, como un conjunto de reportes y notas de aplicación de gran utilidad.
3- Trabajos de tesis relacionados con el tema realizados anteriormente en el CENIDET.
4- Libros de texto en el área de control de accionamientos.
A continuación se mencionan algunos trabajos relacionados con el tema de la utilización
de algoritmos de control vectorial en motores de inducción. En cada caso se agrega una
breve descripción de la publicación.
3
Capítulo 1
Introducción
a) Título: “Control de motores de ca de tipo inducción usando el principio de
Voltaje/Frecuencia Constante y la técnica de PWM con vectores espaciales con
TMS320C240”. Reporte de aplicación: SPRA284A. Texas Instruments [5].
Autores: Zhenyu Yu y David Figoli.
Este trabajo describe un sistema completo de control de motores de inducción usando un
procesador de la familia TMS320C2xx. Aunque las técnicas de control y generación de
PWM usadas en el mismo no son las que se utilizarán en la tesis, la explicación teórica
brindada fue de gran utilidad para el desarrollo del trabajo.
b) Título: “Field Orientated Control of 3-Phase AC-Motors”. Nota de aplicación: BPRA073.
Texas Instruments [16].
Este artículo brinda un panorama general del control por campo orientado, además de
proponer un sistema de control de motores de inducción usando el principio de campo
orientado, explicando de forma simple todo el fundamento matemático de esta técnica.
c) Trabajo de tesis: Modelado y Simulación de un Sistemas Impulsor de Motores de Inducción
Trifásicos. Tesis de maestría, 1994 [6].
Autor: Gerardo Vicente Guerrero Ramírez.
En esta tesis se obtuvieron modelos basados en la Teoría del Marco de Referencia,
simulando diferentes condiciones de operación de cada uno de los convertidores
electrónicos que componen el sistema impulsor propuesto y el motor de inducción
utilizado. Del conocimiento de sus características y de su adecuada interpretación depende
la toma de decisiones correctas para la selección del equipo de alimentación, protección,
control y carga del motor de inducción tipo jaula de ardilla.
d) Trabajo de tesis: Controladores de Motores de Inducción: Un Análisis Comparativo. Tesis de
maestría, marzo 2001 [7].
Autor: Miguel Ángel Méndez Bolio.
Este trabajo de tesis aborda el estudio de los motores de inducción, de sus diferentes
métodos de control, así como la elaboración de programas computacionales (con la ayuda
del paquete computacional Matlab/SimulinkTM ) para la simulación digital de la operación
de los diferentes esquemas de control analizados.
e) Libro de texto: “Vector Control of AC Machines”
Autor: Peter Vas.
Este libro se toma como base en el desarrollo de la tesis porque se discute ampliamente el
control vectorial. Presenta tres posibles marcos de referencia a los que puede ser orientado
el campo y son: marco de referencia orientado al flujo del estator, del rotor y/o de
magnetización. Pone gran énfasis en presentar un tratamiento matemático y físico
detallado y unificado, utilizando la notación de fasores espaciales [2].
4
Capítulo 1
Introducción
1.3 Organización del trabajo de tesis
El trabajo de tesis incluye una introducción teórica sobre el motor de inducción de rotor
devanado y la descripción teórica de control por campo orientado. Se obtiene una serie de
simulaciones de los modelos del MIDA en lazo abierto y cuando se aplica el control.
Finalmente se establecen las conclusiones. Con este fin se ha estructurado el mismo en los
siguientes capítulos:
El Capítulo 2 muestra una clasificación de los motores eléctricos, continuando con una
introducción teórica del principio de funcionamiento del motor de inducción, mostrando
las ecuaciones de voltaje, par del motor trifásico y bifásico. Se presenta el motor de
inducción en configuración doble alimentado. Así como una introducción teórica a los
distintos marcos de referencia (MR) y la aplicación del MR seleccionado al MIDA.
En el Capítulo 3 se realiza el análisis del flujo de potencias, el análisis en estado
estacionario y el modelado dinámico del MIDA en lazo abierto. En el análisis del flujo de
potencias se establecen los signos de los flujos de las potencias que nos sirven como base
en el desarrollo del trabajo de tesis. En el análisis del MIDA en estado estacionario se
obtienen los parámetros que caracterizan al motor y por último, se modela al MIDA en el
marco de referencia fijo al estator en lazo abierto.
El Capítulo 4 ofrece una explicación de los métodos clásicos de control de un motor de
inducción de rotor devanado (MIRD), así como el marco teórico necesario para
comprender el funcionamiento de un sistema de control vectorial por campo orientado,
explicando el funcionamiento de esta técnica y la fundamentación matemática de la
misma.
El Capítulo 5 describe la simulación del sistema de control, explicando el funcionamiento
de cada uno de los bloques que lo integran. Se presenta un sistema de control de velocidad
para el MIDA mediante la técnica de control por campo orientado. Se brindan los
principales resultados obtenidos desde el punto de vista de simulación, en la
programación del algoritmo de control de velocidad del MIDA.
Por último, se muestran las conclusiones y recomendaciones del trabajo, la bibliografía
utilizada y un conjunto de anexos que comprenden los programas en MATLAB
elaborados en el trabajo.
1.4 Resultados del trabajo de tesis
Los puntos importantes de la primera fase del trabajo de tesis (capítulo 3) fueron:
• El análisis del flujo de potencias en el MIDA, donde se establecieron los signos de
las potencias, indicando el flujo de las potencias para las velocidades subsíncronas y super-síncronas.
• El análisis del MIDA en estado estacionario, dando como resultado tres pares
electromagnéticos que nos indican el comportamiento del modo motor.
5
Capítulo 1
•
Introducción
Y concluyendo está primera fase con la simulación del MIDA en lazo abierto en el
marco de referencia fijo al estator.
En la segunda fase (capítulo 5) se aplicó el control vectorial orientado al flujo del estator al
MIDA y se obtuvo la simulación del control de velocidad del motor de inducción doble
alimentado. Con las gráficas de la simulación se demuestra el objetivo principal de la tesis
que es el control de velocidad de un MIDA.
En este trabajo de tesis el modelo del convertidor es ideal, ya que se supone que se
generan las ondas de voltaje del rotor senoidales iguales a las ondas de referencia
correspondientes a las generadas por el controlador. Dando pie a trabajos futuros como el
control de velocidad para el MIDA utilizando un convertidor de flujo de potencia
bidireccional. Otro trabajo posible es al análisis del MIDA con sistemas de alimentación
no balanceados.
6
CAPÍTULO 2
GENERALIDADES SOBRE EL MOTOR DE INDUCCIÓN DE ROTOR
DEVANADO (MIRD) Y SU USO COMO MOTOR DE INDUCCIÓN
DOBLEMENTE ALIMENTADO (MIDA)
INTRODUCCIÓN
En este capítulo se muestra una clasificación general de los motores eléctricos, así como
una introducción teórica del principio de funcionamiento del motor de inducción
trifásico, mostrando sus ecuaciones de par, voltaje, enlaces de flujo, etc. Continuando con
una introducción teórica de los marcos de referencia y por último se presenta la
aplicación del marco de referencia seleccionado al MIDA, el cual utiliza un modelo
matemático bifásico equivalente.
2.1 Clasificación de los motores eléctricos
Una máquina eléctrica se compone de dos partes principales, un estator y un rotor que están
separados entre sí por una pequeña capa de aire uniforme conocida como entrehierro. Está
máquina eléctrica es un dispositivo electromecánico que puede convertir energía eléctrica en
mecánica (modo motor) o energía mecánica en eléctrica (modo generador). Esté dispositivo
electromecánico se compone de un sistema que se forma de un subsistema eléctrico, un
subsistema mecánico y un medio por el cual ambos subsistemas puedan interactuar.
Para lograr el proceso de conversión de energía eléctrica en mecánica o de la energía
mecánica en eléctrica, son necesarios los siguientes tres elementos [1]:
1. Un campo magnético.
2. Un conductor.
3. Y la circulación de una corriente en el conductor que se coloca
perpendicular al campo magnético
7
Capítulo 2
Generalidades sobre el MIRD y su uso como MIDA
La figura 2-1 muestra una clasificación general de los motores eléctricos [13]
MOTORES
ELÉCTRICOS
CORRIENTE ALTERNA (CA)
CORRIENTE DIRECTA (CD)
SÍNCRONO
ASÍNCRONO
INDUCCIÓN
JAULA DE
ARDILLA
ROTOR
DEVANADO
SIN
CONVENESCOBILLAS CIONAL
HISTÉRESIS
DE PASO
RELUCTANCIA
Figura 2- 1. Clasificación de los motores eléctricos.
Generalidades sobre el motor de inducción de rotor devanado (MIRD)
Este trabajo está orientado al control de motores de corriente alterna (ca), específicamente
a un motor asincrónico o de inducción, de tipo “rotor devanado”. Estos motores son más
robustos y económicos que los motores equivalentes de cd, debido fundamentalmente a
que no se necesita una fuente de corriente externa al rotor para crear un campo magnético
en éste.
El rotor devanado, tiene un núcleo de acero laminado sobre el cual se colocan uno o varios
embobinados con alambre de cobre u otro material conductor. Las tres fases de los
embobinados del rotor usualmente se conectan en Υ (estrella) y sus extremos se conectan
a unos anillos deslizantes aislados que están montados sobre el eje. Las escobillas de
carbón que se recargan sobre dichos anillos hacen que las terminales del rotor se conecten
al exterior del motor (figura 2-2).
Al motor de inducción se le suministra corriente eléctrica alterna a los devanados del
estator y mediante el fenómeno de inducción se inducen corrientes en las espiras del rotor
teniendo así la interacción de dos campos magnéticos, esto es, el del rotor y el estator, lo
cual origina un par electromagnético aprovechándose dicho par en la flecha para impulsar
una carga mecánica acoplada al eje del rotor.
Colocando resistencias variables en serie a los bobinados del rotor se consigue disminuir
las corrientes de arranque. Estas resistencias también afectan al par de arranque de la
máquina; es decir, a un aumento progresivo de resistencia del rotor, aumentará
progresivamente el par de arranque hasta un punto en el que alcance el par máximo. Si se
continua aumentando la resistencia del rotor más allá del par máximo, se producirán
disminuciones del par de arranque.
8
Capítulo 2
Generalidades sobre el MIRD y su uso como MIDA
Is
FUENTE
TRIFÁSICA
ESTATOR
IR
ESCOBILLAS
ROTOR
ANILLOS DE
DESLIZAMIENTO
Figura 2- 2. Motor de inducción de rotor devanado.
2.2 Principios de funcionamiento del Motor de Inducción (MI)
El principio de operación del motor de inducción se puede ilustrar simplemente utilizando
un aparato como el que se muestra en la figura 2-3a [1].
Suspensión
Imán
permanente
Sentido de las
corrientes parásitas
inducidas
Lámina
giratoria
Cojinete
Pivote
Rotación
del imán
Rotación
del disco
Placa de hierro
a)Vista frontal
b) Vista Superior
Figura 2- 3. Principio de operación del motor de inducción.
Un imán permanente está suspendido por encima de un disco de cobre o aluminio que
gira por medio de un pivote que se encuentra en medio de una serie de cojinetes en una
plancha de hierro fija. La plancha de hierro logra que el campo del imán permanente se
complete. El pivote debe presentar rozamiento mínimo y el imán permanente debe tener
una densidad de flujo suficiente para mover el disco. Así, cuando el imán gira, el disco
situado debajo de él gira con él; es decir, el disco sigue el movimiento del imán, como se
indica en la figura 2-3b, debido a las corrientes parásitas inducidas que se producen por el
movimiento relativo entre un conductor (el disco) y un campo magnético. Las corrientes
parásitas inducidas tienden a producir un polo sur en el disco en el punto situado bajo el
polo norte del imán y un polo norte en el punto situado debajo del polo sur del imán.
Mientras que el imán continúe moviéndose se seguirán produciendo corrientes parásitas y
polos de polaridad opuesta en el disco situado debajo de él. Por consiguiente, el disco gira
en el mismo sentido que el imán, pero gira a una velocidad menor que la del imán. Si el
disco llegase a girar a la misma velocidad que el imán, entonces no habría movimiento
9
Capítulo 2
Generalidades sobre el MIRD y su uso como MIDA
relativo entre el conductor y el campo magnético, y por consiguiente, no se producirían
corrientes parásitas en el disco.
Se usan dos términos para definir el movimiento relativo del rotor y los campos
magnéticos. Uno es la velocidad de deslizamiento, que se define como la diferencia entre
la velocidad síncrona y la velocidad del rotor, y el otro es el deslizamiento que es la
velocidad relativa expresada en porcentaje.
Principios de funcionamiento de la máquina de inducción doble alimentada
La máquina de inducción doble alimentada (MIDA), está formada por una máquina de
inducción de rotor devanado, se caracteriza porque tiene su estator conectado a una fuente
de alimentación de frecuencia constante y su rotor conectado a un convertidor estático
bidireccional. La configuración física de una máquina de inducción doblemente
alimentada se muestra en la figura 2-4.
La MIDA tiene unas ventajas distintas sobre la convencional máquina jaula de ardilla. La
MIDA puede estar alimentada y controlada desde el estator o desde el rotor o desde
ambos. De las diferentes combinaciones posibles, el control del lado del rotor es la parte
ventajosa ya que el convertidor de potencia sólo necesita manipular la potencia de
deslizamiento.
Vabc
Vabcr
s
CONVERTIDOR
DE FLUJO DE
POTENCIA
BIDIRECCCIONAL
Iabcs
Iabcr
τ em
Figura 2- 4. Configuración física de una MIDA.
Las fases del estator crean un campo magnético en el entrehierro, el cual gira a la
velocidad de la frecuencia del estator (velocidad síncrona, ωs). La formación de un
segundo campo magnético alrededor del rotor se induce a través del entrehierro. Como
consecuencia de la acción de estos dos campos, el rotor comienza a girar en la dirección
del campo del estator, pero a una velocidad menor (velocidad sub-síncrona). Si el rotor
gira a la misma frecuencia que el estator, entonces el campo del rotor pudiera estar en fase
con el campo del estator y no se produciría la inducción de las corrientes del rotor.
Cuando el rotor supera la velocidad del campo giratorio del estator, el motor pasa de
velocidad sub-síncrona a velocidad super-síncrona. Si el motor está a velocidad subsíncrona la potencia del rotor fluye por el convertidor estático hacia la red, recuperando de
esta manera la potencia de deslizamiento. La diferencia entre la frecuencia del estator y la
mecánica se denomina frecuencia de deslizamiento.
10
Capítulo 2
Generalidades sobre el MIRD y su uso como MIDA
Mediante esta configuración, el sistema resulta muy atractivo para aquellas aplicaciones
donde el intervalo de velocidad es limitado y donde la recuperación de energía es un
factor dominante. Se aprovecha una de las ventajas sobresalientes que presentan este tipo
de máquinas de inducción (MIDA), la cual consiste en posibilitar el control, en forma
desacoplada, de las potencias activas y reactivas generadas o absorbidas, utilizando técnicas de
control vectorial en el control de la corriente rotórica. Otra ventaja de esta configuración es
la baja potencia del convertidor ya que se encuentra en el circuito rotórico.
2.2.1. Ecuaciones físicas
Se considera una máquina de inducción trifásica, simétrica, de dos polos, conectada en Y,
donde los devanados del estator son idénticos, distribuidos a lo largo de la periferia del
stator, desplazados 120º eléctricos entre sí, con N s vueltas equivalentes y resistencia R s .
De forma análoga son los devanados del rotor, como se ilustra en el diagrama
esquemático (figura 2-5), mostrando la posición física de los devanados del estator y del
rotor cilíndrico. Además se supone en la máquina de inducción un circuito magnético
lineal; es decir, la permeabilidad del núcleo se considera infinita, y además, la saturación,
las pérdidas en el hierro y el efecto de las ranuras se desprecian [11].
eje bs
as ′
bs
eje br
bs
ar ′
cs
ωr
eje ar
br
as
θr
cr
eje as
cr ′
br ′
bs′
cs′
ar
eje cs
cs
as
eje cr
b)
a)
Figura 2- 5. Diagrama esquemático del motor de inducción trifásico. a)Esquemático de las fases
b) esquemático de polos
De la figura anterior se observan los tres devanados de estator representados por los
círculos as-as’, bs-bs’ y cs-cs’. De la misma forma los devanados de rotor se representan
por los círculos ar-ar’, br-br’ y cr-cr’. El flujo magnético que produce cada uno de los
devanados del estator y rotor se representan por los ejes magnéticos as, bs, cs para el
estator y ar, br, cr para el rotor. La velocidad a la cual se mueve el rotor se representa por
ωr. Y el ángulo θr entre los ejes magnéticos de estator y rotor de la misma fase (as y ar)
representa la posición angular del rotor.
Una forma equivalente de representar el diagrama esquemático del motor de inducción es
su diagrama eléctrico, el cual nos facilita la obtención de sus ecuaciones. La figura 2-6
muestra una inclinación del circuito eléctrico derecho con la finalidad de enfatizar el
desfasamiento existente entre el estator y rotor.
11
Capítulo 2
Generalidades sobre el MIRD y su uso como MIDA
i cr
i bs
i cs
i br
V cs
Rs
+
Ns
Rs
+
+
V bs
Rr
+
V cr
Vbr
Rr
Nr
Nr
Ns
Nr
Ns
i as
Rr
Rs
V as +
+
i ar
V ar
Figura 2- 6. Diagrama eléctrico de los devanados del estator y rotor del motor de inducción trifásico.
Una vez conocidos los parámetros físicos de la máquina, se plantearán las ecuaciones de
los voltajes inducidos y los voltajes aplicados en los devanados del estator y rotor, a partir de
estas ecuaciones se podrán determinar las demás variables de interés, como son las
corrientes, el par electromagnético, la velocidad, etc.
Las ecuaciones del motor de inducción pueden consultarse en varios libros referentes al
tema. En esta tesis se utiliza la notación que usa Krause [11]. Se denota v sabc , i sabc y λsabc a
los voltajes, corrientes y enlaces de flujo del estator respectivamente. De igual manera para
r
r
), corrientes ( i abc
) y enlaces de flujo ( λrabc ) del rotor.
los voltajes ( v abc
2.2.2. Ecuaciones de voltaje
Para obtener las ecuaciones dinámicas del subsistema eléctrico es necesario aplicar la ley
de voltajes de Kirchhoff en cada una de las mallas de la figura 2-6. Así las ecuaciones
voltaje del estator y rotor, en variables de máquina son:
v as = i as R s + dtd λ as
v bs = i bs R s + dtd λ bs
(2. 1)
v cs = i cs R s + λ cs
d
dt
v ar = i ar R r + dtd λ ar
v br = i br R r + dtd λ br
(2. 2)
v cr = i cr R r + dtd λ cr
donde:
s
r
R
denota las variables y parámetros asociados al estator,
denota las variables y parámetros asociados al rotor,
es la resistencia de devanado.
Las ecuaciones (2.1) y (2.2) se pueden escribir en forma vectorial y son:
v sabc = R s ⋅ i sabc + ρλsabc ,
r
r
v abc
= R r ⋅ i abc
+ ρλrabc .
12
(2. 3)
(2. 4)
Capítulo 2
Generalidades sobre el MIRD y su uso como MIDA
donde ρ es el operador de derivación (d dt ) y v sabc , i sabc y λsabc son vectores (3x1)
definidos por:
v
s
abc
 v as 
i as 
 λ as 




s
s
=  v bs  ; i abc = i bs  ; λ abc = λ bs  .
 v cs 
i cs 
 λ cs 
y abc representa las tres fases del motor. De forma similar se representan las variables del
r
r
rotor v abc
, i abc
y λrabc .
Las matrices de resistencias (3x3) del estator y rotor, son diagonales, con elementos en la
diagonal iguales y están dadas por:
R s
R s =  0
 0
0
Rs
0
0
0  ,
R s 
(2. 5)
R r
R r =  0
 0
0
Rr
0
0
0  .
R r 
(2. 6)
Los enlaces de flujo para un sistema magnético lineal son:
λ = L⋅i
(2. 7)
y expresando en forma matricial, los enlaces de flujo de los devanados del estator y rotor,
en términos de las inductancias y corrientes de los devanados, es:
λsabc   L s
 r =
T
λ abc  (L sr )
L sr  i sabc 
 r .
L r  i abc

(2. 8)
Las siguientes expresiones son de utilidad para relacionar el acoplamiento magnético de la
máquina de inducción. Ver detalles en [11, p. 166], [18, p. 44]. Donde la estructura de las
submatrices de las inductancias de los devanados del estator y rotor, se expresan en
Henrios (H) y son:
L ls + L ms
L s =  − 12 L ms
 − 12 L ms
L lr + L mr
L r =  − 12 L mr
 − 12 L mr
− 12 L ms
L ls + L ms
− 12 L ms
− 12 L mr
L lr + L mr
− 12 L mr
− 12 L ms 
− 12 L ms  ,
L ls + L ms 
(2. 9)
− 12 L mr 
− 12 L mr  , y
L lr + L mr 
(2. 10)
Las inductancias mutuas (estator a rotor) dependen del ángulo del rotor y
representándolas en forma matricial, se tiene:
13
Capítulo 2
Generalidades sobre el MIRD y su uso como MIDA
L sr = [L rs ] T
donde:
L ls
L lr
L ms
L mr
L sr
L ls + L ms
L lr + L mr
θr

2π 
2π  


cos θ r
cos θ r +
 cos θ r −


3
3 




2π 
2π  


= L sr ⋅ cos θ r −
cos θ r
cos θ r +


3 
3 

 

cos θ + 2π  cos θ − 2π 

θ
cos
r
r
  r

3 
3 

es la inductancia de dispersión de los devanados de estator,
es la inductancia de dispersión de los devanados de rotor,
es la inductancia de magnetización de los devanados de estator,
es la inductancia de magnetización de los devanados de rotor,
es la inductancia de mutua entre los devanados de estator y rotor,
es la inductancia propia de los devanados de estator,
es la inductancia propia de los devanados de rotor, y
es la posición angular del rotor.
Estas inductancias se definen de la siguiente forma:
N 2 πµ rl
N 2 πµ rl
Lmr = r ⋅ 0 ,
Lms = s ⋅ 0 ,
2
2
g
g
Ns
Nr
µ
donde:
(2. 11)
Lms =
N s N r πµ0 rl
⋅
,
2 2
g
es el número de vueltas del devanado del estator,
es el número de vueltas del devanado del rotor,
es la permeabilidad en el entrehierro,
es el radio a la mitad del entrehierro,
es la longitud axial del entrehierro, y
es la longitud uniforme del entrehierro.
r
l
g
2.2.3. Ecuación del par
Obteniendo la derivada de los enlaces de flujo para cualquier fase de los devanados del
estator o rotor ( λsabc ó λrabc ), se tiene:
d
dt
λ = ( dtd L ) ⋅ i + L ⋅ ( dtd i ) .
(2. 12)
y desarrollando el primer término del lado derecho de la ecuación (2.12) mediante la
regla de la cadena, se tiene:
d
dt
L=
d
dθ r
L ⋅ dtd θ r
(2. 13)
donde θr es la posición angular del rotor.
El segundo término del lado derecho de la ecuación (2.13) es la velocidad angular del
rotor, es decir:
d
dt
donde n P =
y
θ r = n P ωr
P
2
nP
es el número de pares de polos de los devanados de estator.
P
son los polos del motor
14
(2. 14)
Capítulo 2
Generalidades sobre el MIRD y su uso como MIDA
Debido a la interacción de dos campos magnéticos (el del rotor y el estator), se origina un
par electromagnético; se aprovecha dicho par en la flecha para impulsar una carga
mecánica acoplada al eje del rotor. Así en el subsistema mecánico, de la ecuación de
movimiento del rotor se obtiene de la ecuación del par inercial
J⋅
dω r
= τ em − τ β − τ L
dt
(2. 15)
De la ecuación (2.15), τ L es el par de carga aplicado de manera externa en la dirección de
la velocidad del rotor y τ β es el par de fricción en dirección apuesta al giro de la
velocidad. El valor del par de carga será negativo en modo motor y positivo en modo
generador.
Expresando la ecuación (2.15) en términos del par electromagnético τ em y la velocidad del
rotor ωr , se tiene:
donde:
τ em = J ⋅ dtd ω r + βω r + τ L
(2. 16)
τβ = β ⋅ ωr
J
β
es la inercia del rotor y de la carga en Kg .m 2 ,
es el coeficiente de fricción viscosa en N .m.s / rad ,
es la velocidad angular del rotor en rad / s ,
ωr
τ L es el par de carga en N.m .
2.3 Introducción a la teoría de los marcos de referencia (MR)
Las ecuaciones del motor de inducción trifásico (sección 2.2), muestran un sistema no
lineal, variante en el tiempo y acoplado. El acoplamiento se presenta por que la derivada
de cualquiera de las variables depende de otras variables (ecuaciones (2.8)-(2-13)).
También se observa que algunas de las inductancias de la máquina están en función de la
posición angular del rotor, por lo que los coeficientes de las ecuaciones diferenciales son
variantes en el tiempo.
El sistema trifásico del motor de inducción tiene ocho variables de estado dando como
resultado un sistema de orden 8. Seis ecuaciones en el subsistema eléctrico y dos en el
subsistema mecánico.
Con la finalidad de reducir la complejidad de estas ecuaciones diferenciales, se ha
empleado a través de los años un modelo matemático equivalente bifásico [2],[11] y [12],
refiriendo las variables del estator y rotor a un marco de referencia arbitrario. Este modelo
matemático equivalente reduce el orden del sistema de 8 a 6. Además permite que sea más
fácil el diseño de una ley de control, y facilita la programación de simulación del sistema.
El modelo matemático equivalente bifásico se obtiene al referir las variables del motor de
inducción a un marco de referencia que puede estar fijo o girando a velocidad síncrona o a
velocidad del rotor.
15
Capítulo 2
Generalidades sobre el MIRD y su uso como MIDA
La transformación matemática de tres a dos fases más utilizada, es conocida como
transformación de Park [12].
Un cambio de variables que logra la transformación de las variables trifásicas de los
elementos de un circuito estacionario al marco de referencia arbitrario de dos fases se
expresa como [11, p. 170]:
( )
f qd 0 = Tqd 0 θ q ⋅ f abc
( )
( )
(2. 17)
Tqd 0 θ q : Ω ⊂ ℜ 3 → ℜ 3 , f qd 0 → Tqd 0 θ q f abc ,
donde
Ω : es el conjunto de valores reales admisibles para las variables físicas
involucradas,
f : representa a cualquier sistema 3φ de variables eléctricas desfasadas
120º eléctricos entre sí (voltajes, corrientes, pares, etc.),
abc: denota el sistema de variables originales,
qd0: denota el sistema de variables resultantes,
θq: denota el ángulo entre el eje q y el eje d girando a velocidad ω,
Tqd0(θq): es la matriz de transformación.
La matriz de transformación se define como [11], [12]:
( )
Tqd 0 θ q
donde el término
2
3

cos θ q

2
=  sin θ q
3
 1
 2

2π 
2π  


cos θ q −
 cos θ q +

3 
3 


2π 
2π  


sin  θ q −
 sin  θ q +

3
3 




1
1

2
2

(2. 18)
es un factor constante que se utiliza para igualar las amplitudes de las
variables trifásicas fabc y las variables bifásicas fqd0.
Las relaciones trigonométricas entre las variables se muestran a continuación:
Figura 2- 7. Relación entre las variables trifásicas (abc) y bifásicas (dq0)
Las nuevas variables f q y f d están defasadas 90º eléctricos y giran a velocidad arbitraria
ω . La variable f 0 no está asociada con el marco de referencia arbitrario, sólo está asociada
aritméticamente con las variables originales abc, independientemente de θ .
16
Capítulo 2
Generalidades sobre el MIRD y su uso como MIDA
La inversa de la matriz de transformación también se utiliza para obtener nuevamente las
variables trifásicas (voltaje, corriente, par, etc.) del sistema (máquina de inducción). El
cambio de variables bifásicas a trifásicas se expresa como:
[
]
f abc = Tqd0 (θ q )
−1
⋅ f qd 0
(2. 19)
La siguiente ecuación muestra la inversa de la matriz de transformación:
[T (θ )]
−1
qd 0
q
 cos θ q
sin θ q
1


= cos(θ q − 23 π ) sin (θ q − 23 π) 1
cos(θ q + 23 π ) sin (θ q + 23 π ) 1


(2. 20)
Al utilizar la matriz de transformación (también conocida como matriz de Park) hay que
tomar en cuenta que en condiciones normales de operación, los circuitos eléctricos
trifásicos son balanceados y simétricos. Además, se asume que la máquina de inducción
trifásica idealizada tiene un entrehierro simétrico.
2.3.1. Modelo de la máquina de inducción en el marco de referencia arbitrario
A partir de un marco de referencia arbitrario (MRA) (figura 2-7) se puede pasar a los
marcos de referencia fijo al estator, fijo al rotor o al giratorio síncrono. Los marcos de
referencia se seleccionan en base a la conveniencia o compatibilidad con la representación
de los elementos del circuito. Los marcos de referencia (MR) más utilizados en el análisis
de la máquina de inducción son: el MR fijo al estator y el MR giratorio síncrono [12].
La transformación de un MRA es un simple cambio de variable y no necesita interpretación
física, frecuentemente se visualiza por medio de relaciones trigonométricas entre las
variables involucradas. Para el modelado de la máquina de inducción trifásica se debe
tomar en cuenta que en condiciones normales de operación, los circuitos eléctricos son
balanceados y simétricos.
Se observa en la figura 2-8, que los ejes correspondientes a las variables del estator están
fijas pero los ejes del rotor giran a una velocidad ωr y los ejes del marco de referencia
arbitrario giran a una velocidad arbitraria ω
Eje q
Eje bs
Eje ar
Eje br
θ
Eje as
Eje d
Eje cr
Eje cs
Figura 2- 8. Relación entre las variables trifásicas y bifásicas en un MRA
17
Capítulo 2
Generalidades sobre el MIRD y su uso como MIDA
La siguiente tabla presenta los valores que debe tomar ω que está en un MRA, para
cambiar a otro marco de referencia
Tabla 2- 1 Marcos de referencia.
Matriz de
transformación
Velocidad del marco
de Referencia (MR)
Interpretación
ω
(arbitraria)
Variables del estator y rotor referidos al
marco de referencia arbitrario
ω=0
Variables del estator y rotor referidos al
marco de referencia fijo al estator
θq = 0 ,
ω = ωr
Variables del estator y rotor referidos al
marco de referencia fijo al rotor
θq = θr ,
ω = ωe
Variables del estator y rotor referidos al
marco de referencia giratorio síncrono
Tqd 0 (θ q )
Tqd 0 (0 )
Tqd 0 (θ r )
θq = θe ,
Tqd 0 (θ e )
En la siguiente sección se describe el modelado del MIDA en un marco de referencia fijo al
estator.
2.4 Ecuaciones del modelo bifásico del MIDA
Modelo bifásico del subsistema eléctrico
a) Ecuaciones de voltaje del estator
Recordando la ecuación (2.3), que es la notación matricial de las ecuaciones de voltaje de
las fases abc de los devanados del estator
v sabc = R s ⋅ i sabc + ρλsabc
(2. 21)
Aplicándole la matriz de transformación Tqd 0 (θq ) (ecuación 2.18) a los voltajes, enlaces de
flujo y corrientes, la ecuación anterior se convierte en:
[
] [λ ] + [T (θ)]R [T (θ)] [i ]
] [
v sqd0 = Tqd 0 (θ) ⋅ ρ Tqd 0 (θ )
La derivada
[T (θ)] [λ ]
−1
qd 0
s
qd 0
−1
s
qd 0
qd 0
s
qd0
−1
qd 0
s
qd0
(2. 22)
se desarrolla mediante la fórmula de derivación de
productos, la cual resulta:
[
] [λ ] = K
ρ Tqd 0 (θ)
−1
18
s
qd 0
Capítulo 2
Generalidades sobre el MIRD y su uso como MIDA


− sin θ

2π 


= − sin  θ −


3 


2π 
 − sin  θ +

3 




0
−1
0  ⋅ dtd θ ⋅ λsqd 0 + Tqd 0 (θ q ) ρλ sqd 0


0

cos θ
2π 

cos  θ −

3 

2π 

cos  θ +

3 

[
] [
] [
]
(2. 23)
Sustituyendo la ecuación (2.23) en (2.22), y aplicando las siguientes identidades
trigonométricas:
2π 
2π  3

2
cos 2 θ + cos 2  θ −
= ,
 + cos  θ +
3 
3  2


2π 
2π  3

2
sin 2 θ + sin 2  θ −
 + sin  θ +
= ,
3 
3  2


2π  
2π 
2π  
2π 


sin θ ⋅ cos θ + sin  θ −
 cos θ −
 + sin  θ +
 cos θ +
 = 0,
3  
3 
3  
3 


2π 
2π 


sin θ + sin  θ −
 + sin  θ +
 = 0,
3 
3 


2π 
2π 


cos θ + cos θ −
 + cos θ +
 = 0,
3 
3 


El modelo bifásico del subsistema eléctrico del estator resultante es:
s
qd0
v
 0 1 0
= ω ⋅ − 1 0 0 ⋅ λsqd 0 + ρλsqd 0 + R sqd 0 ⋅ i sqd 0 ,
 0 0 0
(2. 24)
donde:
ω=
d
dt
θ
R sqd 0
y
1 0 0
= R s ⋅ 0 1 0
0 0 1
b) Ecuaciones de voltaje del rotor
De manera análoga se obtiene el modelo bifásico del subsistema eléctrico del rotor. De las
ecuaciones de voltaje de las fases abc de los devanados del rotor en forma matricial
(ecuación 2-4), se tiene:
r
r
v abc
= R r ⋅ i abc
+ ρλrabc ,
(2. 25)
y aplicándole la matriz de transformación (ecuación 2.18) a los voltajes, enlaces de flujo y
corrientes, la ecuación (2-25) se convierte en:
[
][
] [ ] [
]
[
] [ ]
r
r
r
.
= Tqd 0 (θ − θ r ) ρ Tqd 0 (θ − θ r ) −1 λrqd0 + Tqd 0 (θ − θ r ) R qd0
v qd0
Tqd 0 (θ − θ r ) −1 i qd0
19
(2. 26)
Capítulo 2
Generalidades sobre el MIRD y su uso como MIDA
Al igual que en la ecuación de voltaje del estator, el término de la derivada se desarrolla,
dando como resultado:
] [λ ] = K
[
ρ Tqd 0 (θ − θ r )

 − sin (θ − θ )
r

2π 


=  − sin  θ − θ r −

3 


 − sin  θ − θ + 2 π 
r

3 

−1

0 
0  ⋅

0

cos (θ − θ r )
2π 

cos  θ − θ r −

3 

2π 

cos  θ − θ r +

3 

r
qd 0
d
dt
(θ − θ r ) ⋅ [λrqd 0 ] + [Tqd 0 (θ − θ r )]−1 [ρλ rqd 0 ]
(2. 27)
Sustituyendo la ecuación (2.27) en (2.26), tenemos:
v
r
qd0
 0 1 0
r
r
= (ω − ω r ) ⋅ − 1 0 0 ⋅ λrqd0 + ρλrqd0 + R qd0
⋅ i qd0
 0 0 0
(2. 28)
donde:
ω − ωr =
d
dt
θ − θr
d
dt
R
y
r
qd0
1 0 0 
= R r ⋅ 0 1 0
0 0 1
c) Enlaces de flujo bifásicos
El primer renglón de la ecuación (2.8), se refiere a los enlaces de flujo trifásicos (abc), a
dicha matriz se le aplica la ecuación (2.18), para obtener los enlaces de flujo qd0 en el
estator
[
]
r
λsqd0 = Tqd 0 (θ) ⋅ L s ⋅ i sabc + L sr ⋅ i abc
.
(2. 29)
Usando las transformaciones inversas apropiadas para reemplazar las corrientes trifásicas
(abc) del estator y rotor, por sus correspondientes corrientes bifásicas (qd0), la ecuación
(2.29) es:
[
]
[
]
λsqd 0 = Tqd 0 (θ) ⋅ L s ⋅ Tqd 0 (θ )
λ
s
qd 0
L ls + 32 ⋅ L s

0
=

0
−1
[
]
[
]
⋅ i sqd 0 + Tqd 0 (θ) ⋅ L sr ⋅ Tqd 0 (θ − θ r )
0
 32 ⋅ L sr
0  ⋅ i sqd 0 +  0
 0
L ls 
0
L ls + 32 ⋅ L s
0
0
3
2 ⋅ L sr
0
−1
r
⋅ i qd
0
0
r
0 ⋅ i qd
0
0
(2. 30)
De forma similar, a los enlaces de flujo abc en el rotor correspondiente al segundo renglón
de la ecuación (2.8), se le aplica la matriz de transformación para obtener los enlaces de
flujo qd0 en el rotor, es decir:
[
r
λrqd 0 = Tqd 0 (θ ) ⋅ (L sr ) ⋅ i sabc + L r ⋅ i abc
T
20
]
(2. 31)
Capítulo 2
Generalidades sobre el MIRD y su uso como MIDA
Usando las transformaciones inversas apropiadas, la ecuación (2.31) se convierte en:
[
]
[
]
λrqd 0 = Tqd 0 (θ − θ r ) ⋅ (L sr ) ⋅ Tqd 0 (θ)
λ
r
qd 0
 32 ⋅ L sr

= 0
 0
T
0
3
2 ⋅ L sr
0
−1
[
]
[
]
⋅ i sqd 0 + Tqd 0 (θ − θ r ) ⋅ L r ⋅ Tqd 0 (θ − θ r )
0
L lr + 32 ⋅ L r
0 ⋅ i sqd 0 + 
0

0
0
0
L lr + 32 ⋅ L r
0
0
r
0  ⋅ i qd
0
L lr 
−1
r
⋅ i qd
0
(2. 32)
Las relaciones de los enlaces de flujo del estator y del rotor de las ecuaciones (2.30) y (2.32)
se pueden expresar de manera compacta como:
λ qs  L ls + L m
λ  
0
 ds  = 
λ qr   L m
  
0
λ dr  
0
L ls + L m
0
Lm
0
L lr + L m
Lm
0
0  i qs 
L m  i ds 
⋅
0  i qr 
  
L lr + L m  i dr 
(2. 33)
y la inductancia de magnetización del lado del estator es:
L m = 32 ⋅ L s = 32 ⋅ L sr = 32 ⋅ L r
(2. 34)
Modelo bifásico del subsistema mecánico
Siguiendo la metodología de Kruase [11], la ecuación para el par electromagnético en el
modelo trifásico se obtiene de la coenergía en el campo magnético.
∂
P
r
τ em =   ⋅ (i sabc ) T ⋅
.
[L sr ] ⋅ i abc
∂θ r
2
(2. 35)
El modelo bifásico del par electromagnético se obtiene al multiplicar las corrientes
trifásicas por sus respectivas transformaciones inversas, y es:
[
P
−1
τ em =   ⋅ (Tqd 0 (θ )) ⋅ i sqd0
2
]
T
⋅
∂
r
.
[L sr ] ⋅ (Tqd 0 (θ − θ r ))−1 i qd0
∂θ r
(2. 36)
Desarrollando la ecuación (2.35) se obtiene el par electromagnético en términos de
corrientes. Se muestra el par electromagnético con diferentes variable pero su valor debe
ser igual. Lo que diferencia un par de otro es las variables que se desea manipular o estén
disponibles:
3 P
τ em =   ⋅   ⋅ (λ qr i dr − λ dr i qr )
2  2
3 P
τ em =   ⋅   ⋅ (λ ds i qs − λ qs i ds )
2  2
3 P
τ em =   ⋅   ⋅ L m ⋅ (i dr i qs − i qr i ds )
2  2
21
(2. 37)
(2. 38)
(2. 39)
Capítulo 2
Generalidades sobre el MIRD y su uso como MIDA
Según la metodología de Ong [12] el modelo bifásico del par electromagnético se obtiene
de la ecuación de potencia de entrada instantánea trifásica, la cual es la suma de los seis
devanados del estator y rotor, como se muestra en la siguiente ecuación
p in = (v as i as + v bs i bs + v cs i cs + v ar i ar + v br i br + v cr i cr )
y su forma bifásica (qd0), la potencia de entrada instantánea es:
3
p in =   ⋅ (v qs i qs + v ds i ds + 2v 0s i 0s + v qr i qr + v dr i dr + 2 v 0 r i 0 r )
2
(2. 40)
Usando las ecuaciones (2-24) y (2-28) para sustituir los voltajes del lado derecho de la
ecuación (2-40). Se obtienen tres tipos de términos: i 2 r , i ⋅ ρλ y ωλi , el primer término
son las pérdidas en el cobre, el segundo término representa la razón de intercambio de la
energía del campo magnético entre los devanados, y último (ωλi) representa la razón de
energía convertida a trabajo mecánico, y se divide entre la velocidad mecánica para
obtener:
3 P  1
τ em =   ⋅   ⋅ 
 2   2   ωr

 ⋅ ω(λ ds i qs − λ qs i ds ) + (ω − ω r )(λ dr i qr − λ qr i dr ) .

[
]
(2. 41)
De está ecuación también se pueden obtener las ecuaciones (2-37), (2-38) y (2-39).
Las ecuaciones de la velocidad y la posición no dependen de variables eléctricas. Así, tanto
para el modelo trifásico (ecuaciones (2.14) y (2.15)) como el modelo bifásico se utilizan las
mismas ecuaciones.
J ⋅ dtd ω r = τ em − βω r − τ L ,
d
dt
(2. 42)
θ r = n P ωr
Así, tanto para el modelo trifásico como el modelo bifásico se
ecuaciones.
utilizan las mismas
2.4.1. Ecuaciones del MIDA en un marco de referencia arbitrario
Las ecuaciones de voltaje bifásicas del estator de un motor de inducción en un marco de
referencia arbitrario son:
v qs = R s i qs + ρλ qs + ωλ ds
v ds = R s i ds + ρλ ds − ωλ qs
(2. 43)
y las ecuaciones bifásicas del rotor
v qr = R r i qr + ρλ qr + (ω − ω r )λ dr
v dr = R r i dr + ρλ dr − (ω − ω r )λ qr
22
(2. 44)
Capítulo 2
Generalidades sobre el MIRD y su uso como MIDA
La matriz de ecuaciones de enlaces de flujo es:
λ qs  L ls + L m
λ  
0
 ds  = 
λ qr   L m
  
0
λ dr  
0
L ls + L m
0
Lm
Lm
0
L'lr + L m
0
0  i qs 
L m  i ds 
 i qr 
0
 
'
L lr + L m  i dr 
(2. 45)
Y el par electromagnético se obtiene de cualquiera de las ecuaciones (2-32), (2-33) y (2-34),
ya que el par es el mismo para cualquier marco de referencia.
En la simulación del MIDA se optó por el marco de referencia fijo al estator, porque las
señales bifásicas de voltaje y corriente del estator como las del rotor deben estar a
frecuencia síncrona; es decir a la frecuencia de la fuente de alimentación (60Hz), lo que nos
garantiza que las señales de la simulación del MIDA son correctas.
2.4.2. Ecuaciones del MIDA en un marco de referencia fijo (MRF) al estator
Ecuaciones de voltaje (Subsistema eléctrico)
Las ecuaciones de voltaje del estator (ecuación (2.42)) y las ecuaciones de voltaje del rotor
(ecuación (2.43)) orientados a un marco de referencia fijo al estator, donde la velocidad
arbitraria es igual a cero (ω = 0) , vea la tabla 2-1, son:
v qs = R s i qs +
v ds
dλ qs
,
dt
dλ
= R s i ds + ds ,
dt
v qr = R r i qr − ω m λ dr +
dλ qr
(2. 46)
,
dt
dλ
v dr = R r i dr + ω m λ qr + dr .
dt
y la matriz de ecuaciones de enlaces de flujo del estator y rotor en forma matricial es la
misma que la ecuación (2.45).
Se observa de las ecuaciones (2.45) y (2.46) que las corrientes y los enlaces de flujo están
relacionadas y ambas no pueden ser variables independientes o de estado, por lo que es
conveniente expresar las ecuaciones de voltaje en términos de las corrientes o de los
enlaces de flujo.
En este caso se seleccionó los enlaces de flujo como variables independientes, entonces la
ecuación (2.46) se expresa como:
23
Capítulo 2
Generalidades sobre el MIRD y su uso como MIDA
i qs  L ls + L M
i  
0
 ds  = 
i qr   L M
  
0
i dr  
0
LM
L ls + L M
0
0
L lr + L M
LM
0
−1
 λ qs 
L M  λ ds 
⋅
 λ qr 
0
  
L lr + L M  λ dr 
0
(2. 47)
La matriz de la ecuación anterior debe ser no singular; es decir, la determinante de la
matriz debe ser diferente de cero.
Ecuación del Par Electromagnético (Subsistema mecánico)
La expresión del par electromagnético no depende de un marco de referencia en particular
y es el mismo establecido en las ecuaciones (2-37) - (2-39) y son:
3 P
τ em =   ⋅   ⋅ (λ qr i dr − λ dr i qr ),
2  2
3 P
τ em =   ⋅   ⋅ (λ ds i qs − λ qs i ds ) ,
2  2
3 P
τ em =   ⋅   ⋅ L m ⋅ (i dr i qs − i qr i ds ) ,
2  2
donde n P =
(2. 48)
P
y P son los número de polos de la máquina.
2,
Las ecuaciones presentadas en está sección son las que se utilizan en la simulación del
MIDA con la ayuda del software de MATLAB/simulink, donde se obtuvieron las gráficas
de voltajes, corrientes, velocidad, par electromagnético y posición del modelo bifásico.
2.5 Circuito equivalente del Motor de Inducción
En un motor trifásico, las tres fases del estator son idénticas entre sí, por lo que se puede
considerar el circuito de una sola fase para su análisis, lo cual también es válido para el
rotor. El modelo del circuito equivalente por fase de los motores de inducción se muestra
en la figura 2-9. En este modelo de circuito completo todos los parámetros se refieren al
estator [17].
Figura 2- 9. Circuito equivalente por fase de un motor de inducción.
donde, r1 , y, X1 , son la resistencia por fase y la reactancia de dispersión del devanado del
estator, rm representa la resistencia por pérdidas de excitación (o de núcleo) y X f es la
reactancia de magnetización. r2 y X 2 son la resistencia por fase del rotor y la reactancia
24
Capítulo 2
Generalidades sobre el MIRD y su uso como MIDA
de dispersión del devanado del rotor. I1 y I 2 son las corrientes por fase del estator y rotor
respectivamente, I m es la corriente de magnetización y v1 es el voltaje del estator
El circuito equivalente de la figura 2-9 se utilizará en el siguiente capítulo, sólo que se le
agregara la fuente de alimentación del rotor, con la finalidad de realizar el análisis del
MIDA en estado estacionario
Conclusiones
Este trabajo está orientado al control de motores de corriente alterna (ca), específicamente
a un motor asincrónico o de inducción, de tipo “rotor devanado”. Estos motores son más
robustos y económicos que los motores equivalentes de cd, debido fundamentalmente a
que no se necesita una fuente de corriente externa al rotor para crear un campo magnético
en éste.
La máquina de inducción doble alimentada (MIDA), está formada por una máquina de
inducción de rotor devanado. Se caracteriza porque tiene su estator conectado a una
fuente de alimentación de frecuencia constante y su rotor conectado a un convertidor
estático bidireccional.
Las ecuaciones del motor de inducción trifásico (sección 2.2), muestran un sistema no
lineal, variante en el tiempo y acoplado. El acoplamiento se presenta por que la derivada
de cualquiera de las variables depende de otras variables. También se observa que
algunas de las inductancias de la máquina están en función de la posición angular del
rotor, por lo que los coeficientes de las ecuaciones diferenciales son variantes en el tiempo.
Con la finalidad de reducir la complejidad de estas ecuaciones diferenciales, se ha
empleado a través de los años un modelo matemático equivalente bifásico [2],[11] y [12],
refiriendo las variables del estator y rotor a un marco de referencia arbitrario. Este modelo
matemático equivalente reduce el orden del sistema. Además permite que sea más fácil el
diseño de una ley de control, y facilita la programación de simulación del sistema. El
modelo matemático equivalente bifásico se obtiene al referir las variables del motor de
inducción a un marco de referencia que puede estar fijo o girando a velocidad síncrona o a
velocidad del rotor.
El marco de referencia seleccionado en el desarrollo de este trabajo es el marco de
referencia fijo al estator. Los marcos de referencia se seleccionan con base en la
conveniencia o compatibilidad con la representación de los elementos del circuito.
25
CAPÍTULO 3
MOTOR DE INDUCCIÓN DOBLE ALIMENTADO (MIDA)
INTRODUCCIÓN
En este capítulo se realiza el diagrama del flujo de potencias en el MIDA con el objetivo de
obtener un diagrama de flujo de potencias y verificar la posibilidad de recuperación de
energía vía rotórica dependiendo del modo de operación. También se realiza el análisis en
estado estacionario, y el modelado dinámico del MIDA en lazo abierto.
3.1 Flujo de potencias y pérdidas en el estator y rotor
La máquina de inducción puede describirse, como un transformador giratorio. Es un
dispositivo al que se suministra voltajes y corrientes eléctrica trifásicas en forma directa al
estator, y al rotor por inducción o acción de transformador desde el estator.
Una forma más sencilla de entender la conversión de la energía eléctrica en energía mecánica
es a través del diagrama del flujo de potencias (figura 3-1). El diagrama muestra como la
potencia de entrada (potencia activa) fluye a través de la máquina.
Refiriéndose a la figura 3-1 la potencia eléctrica de entrada ( Pe ) fluye de la línea al estator
trifásico. Debido a las pérdidas por el cobre del estator, una porción Pjs es disipada como
calor en los devanados y otra cierta cantidad Pnc es disipada en forma de calor en el núcleo
del estator. La potencia que permanece en este punto se transfiere al rotor por inducción
electromagnética a través del entrehierro entre el estator y rotor. A esta potencia se le
conoce como potencia en el entrehierro ( Pg ) de la máquina.
Después de que la potencia se transfiere al rotor, una tercera porción Pjr se disipa en
forma de calor. Pjr se conoce
como pérdidas en el cobre del rotor
y el resto esta
finalmente disponible en forma de potencia mecánica ( Pm ). Substrayendo una pequeña
cuarta porción Pv , debido a las pérdidas por fricción. Por último, se obtiene PL , que es la
potencia mecánica utilizada por el eje para accionar la carga.
27
Capítulo 3
Motor de Inducción Doble Alimentado
Figura 3- 1. Diagrama del flujo de potencias en un motor de inducción.
El diagrama del flujo de potencias de la figura 3-1 permite identificar y calcular tres
propiedades importantes del motor de inducción y son: (1) la eficiencia, (2) la potencia y
(3) el par electromagnético.
Análisis del flujo de potencias en la máquina de inducción doble alimentada
El control para una máquina de inducción doble alimentada se coloca del lado del rotor.
La MIDA puede operar como motor o como generador, ambos a velocidades sub-síncronas
y super-síncronas [10], se pueden obtener cuatro modos de operación. Con estos
fundamentos se establece la dirección de los flujos, así como los signos de las potencias en
el motor de inducción doble alimentado, que se tendrá como base en el desarrollo de la
tesis. Se recalca que sólo interesa la operación en modo motor, aunque se presentan los
diagramas de flujo de potencia en modo motor y generador.
Con los siguientes diagramas de flujos de potencia (figuras 3-2 hasta 3-5) se explican los
modos de operación del MIDA. En estas figuras Ps es la potencia entregada al entrehierro
desde el estator, Pr es la potencia entregada al entrehierro del lado del rotor y Pm es la
potencia mecánica. Para el intervalo de velocidades sub-síncronas, el deslizamiento se
encuentra dentro del intervalo 0 < s < 1 (ω mr < ωs ) , y para las velocidades super-síncronas
en el intervalo − 1 < s < 0 (ω mr > ωs ) .
Por convención de signos se establece que las potencias que entran al motor se consideran
positivas, mientras las que salen son negativas, por ejemplo:
Pm > 0 Potencia entrante
Pm< 0 Potencia saliente
28
Capítulo 3
Motor de Inducción Doble Alimentado
Motor
Modo de operación sub-síncrono
Cuando la MIDA está funcionando en modo motor, en el intervalo de velocidad subsíncrona ( 0 < s < 1 ), el flujo de la potencia entrante (Ps) se divide en una potencia mecánica
y una potencia del rotor como se observa en la figura 3-2a. Así, Pr se toma de las
terminales del rotor (figura 3-2b). Este modo de operación se conoce como recuperación de
la Potencia de deslizamiento.
Figura 3- 2. Flujo de potencias en modo Motor del MIDA. a) y b) operación a velocidad sub-síncrona.
De la figura anterior se concluye que la potencia en el estator es entrante Ps > 0 , mientras
que la potencia en el rotor y la mecánica son salientes ( Pr < 0, Pm < 0 ).
Modo de operación super-síncrono
Si la velocidad se incrementa dé tal forma que la máquina opere a velocidades supersíncronas (figura 3-3) la potencia del rotor cambia de dirección respecto a la de la
operación.
Figura 3- 3. Flujo de potencias en modo motor. a) y b) operación a velocidad super-síncrona.
Se puede concluir de las dos figuras anteriores que la potencia en el estator es siempre
entrante ( Ps > 0 ). La potencia mecánica nunca será entrante ( Pm < 0 ) y la potencia del
rotor solo será entrante en operación super-síncrona ( Pr > 0 ) y saliente en operación subsíncrona ( Pr < 0 ), estableciendo así los signos de potencias.
29
Capítulo 3
Motor de Inducción Doble Alimentado
Generador
Modo de operación sub-síncrono y super-síncrono
Cuando la MIDA está en modo generador en el intervalo de velocidades sub-síncrona
(figura 3-4) la potencia es entregada al rotor.
a)
b)
Figura 3- 4. Modo generador. a) y b) operación a velocidad sub-síncrona.
Si la velocidad incrementa de manera que la máquina esté operando a velocidades supersíncronas (figura 3-5) entonces la potencia del rotor cambia la dirección respecto a la de la
operación sub-síncrona.
a)
b)
Figura 3- 5. Modo generador. a) y b) operación a velocidad super-síncrona.
Conclusión del flujo de potencias
Se presenta una tabla comparativa de los modos motor y generador a velocidades subsíncrona y super-síncrona, en la cual se puede apreciar los signos de las potencias en cada
caso. Recordando lo establecido en los signos de las potencias, potencias éntrate positivas
y negativas las salientes.
Tabla 3- 1. Velocidades sub-síncrona y super-síncrona.
Modo
Motor
Velocidad sub-síncrona
Velocidad super-síncrona
Ps > 0
Pr < 0
Ps > 0
Pm < 0
Pr > 0
Ps < 0
Pm > 0
Pr > 0
Ps < 0
Pm > 0
Pr < 0
Pm < 0
Generador
30
Capítulo 3
Motor de Inducción Doble Alimentado
Como el objetivo de la tesis es trabajar en modo motor, en ambos casos (velocidad sub y
super-síncrona) la potencia del estator ( Ps ), es entrante. La potencia mecánica Pm , siempre
será saliente y la potencia del rotor Pr , solo será saliente a velocidades sub-síncronas y
entrante a velocidades super-síncronas.
3.2 Análisis del MIDA en estado estacionario
En este apartado se realiza un análisis del funcionamiento del MIDA bajo condiciones de
operación síncrona en estado estacionario. Se proporciona un fasor de voltaje en el estator
por una fuente de alimentación de frecuencia constante y el rotor es excitado por un
voltaje donde la magnitud y la frecuencia pueden variar de forma independiente. La
frecuencia de la fuente tiene un valor que, sí se sobrepone a la velocidad del rotor resulta
un campo giratorio síncrono. El circuito monofásico equivalente del MIDA se muestra en
la figura 3-6 [17].
Figura 3- 6. Circuito equivalente por fase del MIDA.
De la figura 3-6 se observan las siguientes variables:
r1
es la resistencia de fase del estator,
r2
s
es la resistencia de fase del rotor,
→
es el fasor de la corriente del estator,
→
es es fasor de la corriente del rotor,
I1
I2
X1
X2
Xf
→
v1
es el deslizamiento,
es la reactancia de dispersión del devanado del estator,
es la reactancia de dispersión del devanado del rotor,
es la reactancia de magnetización,
es el fasor del voltaje del estator,
→
v 2 es el fasor del voltaje del rotor, y
a
es el ángulo al que desfasará el voltaje del rotor,
El objetivo del análisis del MIDA en estado estacionario es calcular la potencia mecánica y
el par electromagnético a velocidades sub-síncronas y super-síncronas. Se toman en cuenta
las siguientes consideraciones:
31
Capítulo 3
Motor de Inducción Doble Alimentado
a) La máquina tiene un bobinado trifásico simétrico distribuido alrededor de un
entrehierro uniforme para el estator y rotor.
b) El motor es doblemente alimentado como sigue se suministra desde la red de
alimentación un voltaje a frecuencia síncrona al estator y del lado del rotor se
suministra un voltaje a otra frecuencia, generalmente menor a la síncrona, y por
lo tanto operando a velocidad sub-síncrona.
En el análisis general se omiten las pérdidas por fricción del núcleo, y sólo se consideran
las componentes fundamentales de los voltajes y corrientes, al igual que las componentes
fundamentales de las fuerzas magnetomotrices del estator y rotor.
Con respecto al análisis del flujo de las potencias de la sección 3.1, las variables eléctricas
que entran en las terminales del estator y rotor se consideran positivas. La potencia
mecánica ( Pm ) es saliente por lo que se considera negativa y el par electromagnético ( τ em )
es positivo sí está en modo motor.
Del cálculo de los valores de las corrientes del estator y rotor, se determinan los
parámetros de rendimiento del motor mediante las ecuaciones de la tabla 3-2, con la
finalidad de calcular la potencia mecánica total y el par electromagnético total a
velocidades sub y super-síncronas.
Tabla 3- 2. Fórmulas de potencias y pérdidas en un motor de inducción.
Del lado del estator
Potencia activa de entrada ( P1 )1 de la fuente al
estator
Potencia reactiva del estator
→ → 
P1 = ℜe  v 1 I1* 


→
→ 
Q1 = ℑm  v 1 I1* 


(3. 1)
(3. 2)
→ 2
Pérdidas en la resistencia r1 de los devanados del
Pr1 = I1 r1
estator
(3. 3)
Potencia reactiva en la reactancia de fuga X 1 del
estator
(3. 4)
Potencia reactiva en la reactancia de
magnetización ( X f )
→ 2
Q X1 = I1 X 1
→
→ 2
Q Xf = I1 + I 2 X f
Potencia activa entregada al entrehierro desde el Pg1 = P1 − Pr1
estator
Potencia reactiva entregada al entrehierro desde Q g1 = Q 1 − Q X1 − Q Xf
el estator
1
El asterisco (∗) indica el complejo conjugado de la variable.
32
(3. 5)
(3. 6)
(3. 7)
Capítulo 3
Motor de Inducción Doble Alimentado
Del lado del rotor
Potencia activa entregada al del rotor por la
fuente de excitación en el rotor
Potencia reactiva entregada al rotor por la fuente
de excitación en el rotor
 → →
P2 = ℜe  v 2 ⋅ I *2 


→
→


Q 2 = ℑm  v 2 ⋅ I *2 


→ 2
Pérdidas en la resistencia del rotor
Pr 2 = I 2 ⋅ r2
Potencia reactiva en la reactancia de fuga ( X 2 )
Q X2 = I 2 X 2
→ 2
Potencia activa del entrehierro entregada desde
Pg 2 = P2 − Pr 2
el rotor
Potencia reactiva del entrehierro entregada desde Q g 2 = Q 2 − Q X 2
el rotor
(3. 8)
(3. 9)
(3. 10)
(3. 11)
(3. 12)
(3. 13)
Las ecuaciones de las potencias y pérdidas se encuentran en cualquier libro de máquinas
eléctricas, en especial en [9], [17].
Ecuaciones del MIDA en estado estacionario
Por conveniencia se utilizan las variables de las corrientes y de los voltajes del estator y
rotor sin la flecha como superíndice, pero debe recordarse que todas las magnitudes
excepto la potencia mecánica y el par electromagnético son consideradas por fase.
Las ecuaciones que describen el modelo del MIDA en estado estacionario son funciones de
dos variables independientes, a saber: el coeficiente de deslizamiento (s) y la magnitud del
voltaje de excitación del rotor ( v 2 ).
Aplicando un par de carga al eje del rotor, el rotor gira con una velocidad angular ω mr , la
cual corresponde a un deslizamiento s = (ωs − ω mr ) ωs , donde ωs es la velocidad
síncrona.
La corriente del estator, I1 , y la corriente del rotor, I 2 , se determinan a partir de modelo
del circuito de la figura 3-6, donde r2 y X 2 están referidos a los embobinados del estator.
Una vez conocidos los valores de I1 y de I 2 , se determinan los parámetros de
rendimiento del motor mediante las ecuaciones presentadas en la tabla 3-2. Así, al realizar
el análisis de mallas en el circuito de la figura 3-6 y al utilizar el software Matemática se
obtienen las siguientes expresiones:
De la malla I1 , se obtiene:
v1 = [r1 + j(X 1 + X f )]I1 + jX f I 2 ,
33
(3. 14)
Capítulo 3
Motor de Inducción Doble Alimentado
y de la malla I 2
v 2 ja

r
e = jX f I1 +  2 + j(X 2 + X f ) I 2 .
s

s
(3. 15)
Expresando en forma matricial al sistema formado por las ecuaciones (3-14) y (3-15), se
tiene:
jX f
r1 + j(X 1 + X f )
  I   v1 

 1 =  v e ja  .
r2
jX f
+ j(X 2 + X f ) I 2   2 

s


 s 
(3. 16)
Para los valores numéricos de las variables del Motor de inducción utilizado en este
trabajo de tesis el determinante de la ecuación (3.16) es no singular (ver anexo 1), y se
representa como:
∆ = (∆ a ) + (∆ b ) ,
2
donde:
2
(3. 17)
r1 r2
− (X 1 X 2 + X f {X 1 + X 2 }) ,
s
r  rX

∆ b = r1 X 2 + X f r1 + 2  + 2 1 ,
s
s

∆a =
y
(3. 18)
→
v 2 ja v 2 ja v 2
e =
e = s ∠a , y
s
s
e ja = cos(a ) + j sin (a )
Por lo tanto, la corriente I1 del estator se expresa como:
I1 =
+j
1
∆
1
∆
  v 1 r2 X f v 2
X v



sin (a ) + ∆ b  v 1 {X 2 + X f } − f 2 cos (a ) 
+
∆ a 
s
s



  s
(3. 19)
 
Xf v2
X v
1  v r


cos (a )  − j  ∆ b  1 2 + f 2 sin (a ) 
 ∆ a  v 1 {X 2 + X f } −
∆  s
s
s


 
Por otra parte, la corriente I2, de la malla del lado del rotor es:
I2 =
+j
1
∆
1
∆

v2
v
(r1 cos (a ) − {X 1 + X f }sin (a )) + ∆ b  2
∆ a
s
 s

  v2
 ∆ a 
  s

({X 1 + X f }cos (a ) + r1 sin (a )) − v 1 X f  


v


∆ b 2 (r1 cos (a ) − {X 1 + X f }sin (a ))

∆
s

({X 1 + X f }cos (a ) + r1 sin (a )) − v 1 X f   − j 1

(3. 20)
Desarrollando las corrientes I1 e I 2 del estator y rotor respectivamente están en función
del deslizamiento s y de la magnitud de v 2 .
34
Capítulo 3
Motor de Inducción Doble Alimentado
a) Ecuaciones del Estator
La potencia activa de entrada, P1 , se obtiene al multiplicar la parte real de la ecuación
(3.19) y v1 , como se indica en la ecuación (3.1) y es la potencia entregada de la fuente al
estator. Así,
v12
P1 =
∆
 r1 r22
r2 X f2  v1 v 2 X f
2
[∆ b cos(a ) − ∆ a sin (a )]
 2 + r1 (X 2 + X f ) +
−
s 
s∆
s
(3. 21)
La potencia reactiva del estator se obtiene de la ecuación (3.2) y es:
v12
Q1 =
∆
r22
 v1v 2 Xf
[∆a cos(a) + ∆ b sin(a)] (3. 22)
 2 (X1 + Xf ) + (X 2 + Xf )(X1X 2 + Xf [X1 + X 2 ]) +
∆s
s

Las pérdidas, Pr1 , en la resistencia r1 de los devanados del estator se obtiene de
multiplicación del módulo de la corriente y la resistencia del estator (ecuación (3.3)):
2
2
 
 
v X cos(a ) 
v X sin(a )  
v X cos(a ) 
v X sin(a )   
r v
r v
  ∆b  v1(X2 + Xf ) − 2 f
 ∆a  v1(X2 + Xf ) − 2 f
 − ∆b  2 1 + 2 f
  
 + ∆a 2 1 + 2 f
 

s
s
s
s



 s
 


 s

Pr1 = r1  
+

2
2
∆
∆






(3. 23)
Sí se resta a la potencia de entrada (3.21), las pérdidas por el cobre del estator (disipadas
como forma de calor en los devanados) y representadas en la figura 3-6 por r1 (3.23), se
obtiene la potencia activa en el entrehierro ( Pg1 ). Utilizando la ecuación (3.4), se tiene:
Pg1 = −
X f2  r1 v 22 v12 r2  v1 v 2 X f
−
−

∆s
s 
∆  s2


 2r1r2
− ∆ b  (3. 24)
cos(a )[∆ b − 2r1 (X 2 + X f )] + sin(a )

 s

De la ecuación (3.5) se obtiene la potencia reactiva entregada al entrehierro desde el
estator:
Q g1 = −
Xf v

∆ s
2
2
2
(X X
1
f
+ X 12 + r12
)

 
 r1 r2
+ X 2 (X 1 + X f ) − X 1 X f  K
cos (a )
 v v X 
 
 s
− v 12 X 2 X f  − 1 2 f 

s
∆

X
r
r

K + sin (a )X r − 1 2 − X  r + 2   
2 1
f
1

s
s   


(3. 25)
A continuación se obtienen las potencias y pérdidas del MIDA del lado del rotor.
b) Ecuaciones del rotor
Continuado con el circuito equivalente por fase del MIDA de la figura 3-6, el cual está
referido al estator, para calcular las potencias y pérdidas del rotor.
La potencia de entrada del lado del rotor, P2 , se obtiene de la ecuación (3.8) y es la
potencia entregada al rotor por la fuente de excitación del rotor, recordando que
v2 =
v2
s
[cos(a ) + j sin (a )] , la potencia de entrada es:
35
Capítulo 3
P2 =
Motor de Inducción Doble Alimentado
r X
r
v 22  r2 r12 r2 X 1
(X 1 + X f ) + X f  2 1 + X f  r1 + 2
+

2
s
s
∆s  s

 s
  v 1 v 2 X f
[∆ b cos(a ) + ∆ a sin (a )]
 −
∆s

(3. 26)
De la ecuación (3.9) se obtiene la potencia reactiva, Q 2 , entregada al rotor por la fuente de
excitación del rotor, y es:
Q2 =
vv X
v 22 2
r1 (X 2 + X f ) + (X1 + X f )(X1X 2 + X f [X1 + X 2 ]) + 1 2 f [∆ a cos(a ) − ∆ b sin(a )] (3. 27)
2
∆s
s ∆
{
}
De la ecuación (3.10) se obtienen las pérdidas Pr 2 en la resistencia del rotor ( r2 s ), para
después restarlas a la potencia de entrada, con el fin de obtener la potencia activa en el
entrehierro del lado del rotor. Así de la ecuación (3.12) se obtiene:
Pg 2 =
X f2  r1 v 22 v12 r2  v1 v 2 X f 
 2r1 r2

− ∆ b   (3. 28)
 2 −
+
cos a [∆ b − 2r1 (X 2 + X f )] + sin a 
s 
∆  s
∆s 
 s

De manera análoga para obtener la potencia reactiva del entrehierro ( Q g 2 ), se calcula de la
ecuación de la ecuación (3.11) la potencia reactiva ( Q X 2 ) en la reactancia de fuga X 2
para luego restarla a la potencia reactiva de entrada ( Q 2 ). Así de la ecuación (3.13), se
tiene:
Q g2 =
Xf
∆
v

s
2
2
2
(X X
1
f
+ X 12 + r12
)

 r1 r2
 
+ X 2 (X 1 + X f ) − X 1 X f  K
cos a 
 vv X 
 s
  (3. 29)
− v 12 X 2 X f  + 1 2 f 

s
∆

K + sin a X 2 r1 − X 1 r2 − X f  r1 + r2 

s 
s


La obtención de las potencias en el entrehierro Pg1 y Pg 2 , dadas por el estator y rotor
respectivamente, son muy importantes para continuar con el análisis del MIDA en los
modos de operación sub-síncrono y super-síncrona, como se explica en el siguiente punto.
c) Modos de Operación
Modo de operación sub-síncrono ( 0 < s < 1 )
Para indicar que el motor se encuentra en operación sub-síncrona se utiliza el subíndice
“ 2b ”. El número “2”, indica que es una variable del rotor y “b” que está en operación subsíncrona
Se considera nuevamente el circuito equivalente de la figura 3-6, en operación subsíncrona, se alimenta al estator con el voltaje v1 y al rotor con v 2 b = v 2 e ja . Los voltajes
del estator y rotor tienen la misma forma de onda. La frecuencia de la fuente de excitación
del rotor es menor que la frecuencia de la fuente principal o del estator, asegurando de
esta manera la operación sub-síncrona. Así, el voltaje y la corriente del rotor en operación
sub-síncrona son:
v 2 b = v 2 e ja
36
(3. 30)
Capítulo 3
Motor de Inducción Doble Alimentado
I 2b = I 2
Las potencias activa y reactiva activa, P2 b , y reactiva, Q 2 b , entregadas al rotor por la
fuente de excitación del lado del rotor se calculan por las ecuaciones (3.8) y (3.9), y son:
[
] [{ } ]
= ℑm[{v e }⋅ I ] = sQ
P2 b = ℜe v 2 b ⋅ I *2 = ℜe v 2 e ja ⋅ I *2 = sP2
Q 2b
ja
2
*
2
(3. 31)
(3. 32)
2
En modo sub-síncrono estas potencias son iguales a las obtenidas en las ecuaciones (3.26) y
(3.27), multiplicadas por el deslizamiento.
Las pérdidas, Pr 2 b , en la resistencia r2 del devanado del rotor y las pérdidas de la potencia
reactiva, Q X 2 b , en la reactancia de fuga sX 2 en el rotor, son:
2
Pr 2 b = I 2 r2 = sPr 2
(3. 33)
2
Q X 2 b = I 2 sX 2 = sQ X 2
(3. 34)
La potencia Pg 2 b y la potencia reactiva Q g 2 b entregadas al entrehierro desde el rotor son:
Pg 2 b = P2 b − Pr 2 b = sPg 2 = −sPg1
(3. 35)
Q g 2 b = Q 2 b − Q X 2 b = sQ g 2 = −sQ g1
(3. 36)
La potencia mecánica Pm 2 b total se deduce de la potencia en el entrehierro entregada al
estator y rotor, es decir de las ecuaciones (3.24) y (3.35), se tiene:
Pm 2 b = 3(Pg1 + Pg 2 b ) = 3Pg1 (1 − s ) = −3Pg 2 b
1− s
s
(3. 37)
De manera similar se deduce de las ecuaciones (3.25) y (3.34) la potencia reactiva Q m 2 b
trifásica
Q m 2 b = 3(Q g1 + Q g 2 b ) = 3Q g1 (1 − s ) = −3Q g 2 b
1− s
s
(3. 38)
Modo de operación super-síncrono ( − 1 < s < 0 )
Al igual que en la operación sub-síncrona el subíndice “2” indica que es una variable del
rotor y en lugar del subíndice “b”, utilizamos el subíndice “s” para indicar que el sistema
se encuentra en operación super-síncrona.
Se sigue considerando el circuito equivalente de la figura 3-6. Ahora en operación supersíncrona el rotor es alimentado con un voltaje v 2s y tienen una secuencia opuesta al
voltaje de alimentación del estator ( v1 ). La frecuencia del rotor es mayor que la frecuencia
de la fuente principal. Así, v 2s = v 2 ⋅ [cos(a ) − j sin (a )] = v 2 e − ja y la corriente I 2s = I ∗2 .
37
Capítulo 3
Motor de Inducción Doble Alimentado
Se calculan nuevamente las variables para este modo de operación. Las potencias activa,
P2s , y la potencia reactiva, Q 2s , de entregada al rotor por la fuente de excitación son:
[
= ℑm[v
]
] = −sQ
P2s = ℜe v 2 (cos a − j sin a ) ⋅ I ∗2 = sP2
Q 2s
2
(cos a − j sin a ) ⋅ I
∗
2
(3. 39)
2
(3. 40)
Las pérdidas, Pr 2s , en la resistencia r2 del devanado del rotor y las perdidas de la potencia
reactiva, Q X 2s , en la reactancia de fuga − sX 2 en el rotor, son:
2
Pr 2s = I 2 r2 = sPr 2
(3. 41)
2
Q X 2s = − I 2 sX 2 = −sQ X 2
(3. 42)
La potencia, Pg 2s , y la potencia reactiva, Q g 2s , entregadas al entrehierro desde el rotor,
están dadas por las siguientes ecuaciones:
Pg 2s = P2s − Pr 2s = sPg 2 = −sPg1
(3. 43)
Q g 2s = Q 2s − Q X 2s = −sQ g 2 = sQ g1
(3. 44)
Para la operación super-síncrona la potencia mecánica total, Pms , se deduce de las
ecuaciones (3.24) y (3.43)
Pms = 3(Pg1 + Pg 2s ) = 3Pg1 (1 − s ) = −3Pg 2s
1− s
s
(3. 45)
De manera similar se deduce de las ecuaciones (3.25) y (3.44), la potencia reactiva, Q ms ,
trifásica:
Q ms = 3(Q g1 + Q g 2s ) = 3Q g1 (1 + s ) = −3Q g 2s
1+ s
s
(3. 46)
d) Potencia mecánica total
Al observar las ecuaciones (3.37) y (3.45), vemos que la potencia mecánica ( Pm ) obtenida,
es la misma en operación sub-síncrona y operación super-síncrona. Se obtiene Pm de las
ecuaciones (3.24) y (3.37) o de las ecuaciones (3.24) y (3.45). Dicha potencia es:
Pm = −
3(1 − s )X f2  r1 v 22 v12 r2  3(1 − s )v1v 2 X f 
 2 r1r2

− ∆b 
−
 2 −
 cos (a )[∆ b − 2 r1 (X 2 + X f )] + sin (a )
∆
∆
s
s
s
s





(3. 47)
La potencia mecánica Pm se divide en las fuentes de potencia del estator y rotor de
acuerdo a las ecuaciones (3.37) y (3.45). Así, para la operación sub-síncrona y supersíncrona la distribución de potencia para el estator y rotor es, respectivamente:
Pm = 3Pg1 (1 − s )
(3. 48)
1− s
s
(3. 49)
Pm = −3Pg 2
38
Capítulo 3
Motor de Inducción Doble Alimentado
De las ecuaciones anteriores se observa, que la potencia es entregada del estator al
entrehierro para ambas operaciones sub y super-síncrona.
e) Par electromagnético
En el análisis en estado estacionario del motor de inducción se puede utilizar la siguiente
relación de par electromagnético [9, p. 279]:
T=
Pm
Pm
=
ω r ωs (1 − s )
(3. 50)
Donde: s es el deslizamiento,
ωs es la velocidad síncrona en rpm,
ωr
es la velocidad mecánica del eje del rotor en rpm, y
Pm
es la potencia mecánica en Watts.
El par electromagnético obtenido de la sustitución de la ecuación (3.47), que es la potencia
mecánica total, en la ecuación anterior (3.50), se compone de tres pares y son:
1) Par asíncrono constante τ s para un deslizamiento dado, producido por el voltaje
suministrado al estator v1
3 ⋅ X f2 ⋅ v12 ⋅ r2
τs =
ωs ⋅ ∆ ⋅ s
(3. 51)
Utilizando el software de MAPLE (versión 7, año 2001) se obtuvo la curva
característica par-deslizamiento de la ecuación (3.51)
Figura 3- 7. Curva característica Par ( τ s ) & deslizamiento.
En la gráfica de la figura 3-7, el par actúa como par-motor en operación subsíncrona es decir en el intervalo de 0 < s < 1 y como par-regenerador en operación
super-síncrona −1 < s < 0 .
39
Capítulo 3
Motor de Inducción Doble Alimentado
2) Par asíncrono constante τ r para un deslizamiento dado, producido por el voltaje
aplicado al rotor ( v 2 )
3X f2 v 22 r1
ωs ∆s 2
y la gráfica correspondiente a este par es:
(3. 52)
τr = −
Figura 3- 8. Curva característica par ( τ r ) & deslizamiento.
En la figura 3-8, el par actúa como par-regenerador en ambas operaciones sub y
super-síncrona.
3) Par producido por la interacción de los campos del estator y rotor ( τ sr ), se obtiene
de:
3v v X 
r

r r
  (3. 53)
τ = − 1 2 f cos (a ) 2 {X + X }− r {X + X } + sin (a ) 1 2 + X X + X {X + X }
sr
ω s ∆s


 s

1
f
1
2
f


 s

1
2
y su gráfica es:
Figura 3- 9. Curva característica par τ sr & deslizamiento.
40
f
1
2


Capítulo 3
Motor de Inducción Doble Alimentado
De la figura 3-9, el par es producido por la interacción de ambos campos, se observa
que en operación sub-síncrona se tiene un par regenerador, y en modo super-síncrona
un par motor.
4) Par total
El par total es la suma de los tres pares anteriormente descritos.
τ T = τ1 + τ 2 + τ s
(3. 54)
Su gráfica es:
Figura 3- 10. Característica Par total ( τ T ) & deslizamiento.
Se observa que el par total τ T en operación sub-síncrona produce un par-motor y un
par-regenerador en operación super-síncrona.
Para comprender mejor estas gráficas en su interpretación, se dividen los pares
operación sub-síncrona y super-síncrona
Operación subsíncrona ( 0 < s < 1 )
El par τ s (
en
Operación super-síncrona ( − 1 < s < 0 )
) de la figura
El par τ s (
3-7 actúa como par-motor, en este modo de
operación.
regenerador.
El par τ r (
) de la figura 3-8 actúa
como par-regenerador.
El par τ r (
regenerador.
El par producido por la iteración de ambos
campos
del
estator
y
rotor,
τ sr
El par τ sr (
) de la figura 3-9, en este
(
modo produce un par-regenerador.
Y el par total τ T (
) en este
modo de operación produce un par-motor
(figura 3-10).
41
) actúa como par-
) actúa como par-
) es este modo
de operación produce un par-motor.
Y el par total, τ T (
) produce
un par-regenerador (figura 3-10).
Capítulo 3
Motor de Inducción Doble Alimentado
Del análisis en estado estacionario del MIDA, se concluye a través de la gráfica de la figura
3-10, que el par total en operación sub-síncrona actúa como par-motor. El resultado es el
deseado ya que el MIDA se encuentra en modo motor.
3.3 Modelado del motor de inducción doble alimentado en lazo abierto en
un marco de referencia fijo al estator
En este apartado se realiza la simulación del MIDA en lazo abierto en un marco de
referencia fijo al estator, mediante la simulación en MATLAB/Simulink (versión 6.5, 2002).
Se considera una Máquina de Inducción de rotor devanado de 3Hp, trifásica, simétrica, de cuatro
polos y conectada en Y. En el análisis del MIDA se desprecian los efectos capacitivos, sólo se
modelan los efectos inductivos y resistivos para el subsistema eléctrico, para el subsistema
mecánico se considera solamente los efectos de la masa de la flecha, omitiendo los efectos
torsionales y se asume que los efectos de fricción presentes son de tipo viscoso. Se supone
además que el circuito magnético es lineal, es decir, no existe saturación del circuito
magnético y además la fuerza magnetomotriz (fmm) no contiene armónicos.
En la figura 3-12 se muestra el diagrama esquemático del motor de inducción doble
alimentado (MIDA) en lazo abierto.
Vas
Vs
Vbs
∼
Vcs
Vqs
3a2φ
Vds
τ
L
Vr
∼
Var
Vbr
Vcr
Vqr
3a2φ
Modelo
bifásico
del MIDA
Vdr
{
ias
ibs
ics
{
iar
ibr
icr
{
ωr
θr
τem
Figura 3- 11. Diagrama esquemático del MIDA en lazo abierto.
Los valores de los elementos del MI se tomaron de la tabla 4.10-1 de Krause [11] y son:
42
Capítulo 3
Motor de Inducción Doble Alimentado
Tabla 3- 3. Parámetros del MIDA
Parámetros
Valor
Voltaje del estator de línea a línea en rms (Vm)
220 V
Voltaje del rotor (Vmr)
22 V
Frecuencia de línea o frecuencia eléctrica
60 Hz
Resistencias del estator (Rs)
0.435 Ω
Resistencias del rotor (Rr)
0.816 Ω
Reactancia de dispersión del devanado del estator (Xls)
0.754 Ω
Reactancia de dispersión del devanado del rotor (Xlr)
0.754 Ω
Reactancia de magnetización (XM)
26.13 Ω
Inercia del rotor (J)
0.089 kg m2
Coeficiente de fricción viscosa (β)
0 (N m s) / (rad)
Deslizamiento
2.8%
Fuente de alimentación del estator
Se considera una fuente de alimentación trifásica balanceada, con una amplitud v m . Los
voltajes de fase ( v as , v bs , v cs ) se encuentran defasados 120º uno respecto a otro, como se
muestra en las siguientes ecuaciones:
v as = v m cos(ωe t )
(3. 55)
v = v cos(ω t − 2 π )
bs
m
e
3
v cs = v m cos(ω e t + π )
2
3
donde ω e es la velocidad eléctrica del sistema en rad/seg.
Los voltajes trifásicos y bifásicos de la fuente de alimentación del estator se muestran en
las figuras 3-12 y 3-13 respectivamente.
Figura 3- 12. Voltajes de alimentación ( v as , v bs , v cs ) & tiempo en segundos.
43
Capítulo 3
Motor de Inducción Doble Alimentado
Las amplitudes pico de las fases de los voltajes ( v as , v bs , v cs ) de la figura 3-12, son de
aproximadamente 179.6 volts y esto se debe a que el parámetro de voltaje del motor es de
220 VL-L (tabla 3-3). Esté parámetro se transforma mediante VP =
2
3
Vm a valor pico del
voltaje de alimentación por fase. Efectivamente, se observa que los voltajes de fase están
defasados 120º eléctricos entre sí. Las tres fases de los voltajes tienen una frecuencia de 60
Hz.
Por conveniencia se muestra nuevamente la matriz de transformación de la ecuación (2-18)
porque se ocupa al realizar la transformación de la fuente de alimentación trifásica a
bifásica en un marco de referencia fijo al estator, es decir θ q = 0 y es:
cos θ q
2
Tqd 0 (θ q ) =  sin θ q
3
 12
cos(θ q − 23 π) cos(θ q + 23 π)
sin (θ q − 23 π) sin (θ q + 23 π)
1
1

2
2
(3. 56)
La siguiente matriz resulta de hacer θ q = 0 :
1 − 12
2
3
Tqd 0 (0) = 0 −
3
2
1
 12
2
− 12 
3

2 
1
2 

(3. 57)
Y los voltajes bifásicos de la fuente de alimentación, después de transformarlos de tres
fases a dos fases, son:
v qs = 23 v as − 13 v bs − 13 v cs
(3. 58)
v ds = 1 (v cs − v bs )
3
La gráfica 3-13 muestra la fuente bifásica de la ecuación (3.58) en un marco de referencia
fijo al estator:
Figura 3- 13. Voltajes v qs , v ds del estator & tiempo.
44
Capítulo 3
Motor de Inducción Doble Alimentado
Los voltajes bifásicos del estator tienen la misma amplitud de los voltajes trifásicos sólo
que ahora se encuentran defasados 90º eléctricos.
Voltajes de la fuente alimentación del rotor
Para el caso de un motor de inducción jaula de ardilla los voltajes del rotor (ecuación 2.41)
son iguales a cero, pero cuando se trata del análisis del MIDA los voltajes del rotor tienen
un valor generalmente menor a una cuarta parte del valor del voltaje del estator [2].
v ar = v 2 cos(ω r t + θ i )
2π


+ θi 
v br = v 2 cos ω r t −
3


2π


+ θi 
v cr = v 2 cos ω r t +
3


donde:
θi
(3. 59)
es la posición inicial del rotor
ω r es la velocidad eléctrica del rotor en rad/seg
En operación sub-síncrona la frecuencia en el rotor ( f r ) es menor a la síncrona ( f s ), y
ambas frecuencias se relacionan mediante:
fr = s ⋅ fs
ω r = s ⋅ ωe
(3. 60)
donde s, es el deslizamiento y se define como la velocidad relativa entre el campo
magnético y el rotor, expresada en porcentaje [14] es:
s=
donde:
ηsin c − η m
(× 100%) ,
ηsin c
(3. 61)
ηsin c es la velocidad síncrona (velocidad del campo magnético) en rpm, y
ηm
es la velocidad mecánica del eje del rotor en rpm.
En la figura 3-24 se muestran los voltajes de la fuente trifásica del rotor, para un
deslizamiento del 2.8%, la frecuencia del rotor es de 1.68 Hz.
45
Capítulo 3
Motor de Inducción Doble Alimentado
Figura 3- 14. Voltajes v ar , v br , v cr & tiempo.
Las fases de los voltajes ( v ar , v br , v cr ) están defasadas 120º eléctricos una con respecto a
otra, y tienen una amplitud pico de 17.96 volts y se obtiene de la relación VP =
2
3
Vmr ,
como en el caso de la fuente trifásica del estator.
La figura 3-15 muestra los voltajes bifásicos de la fuente. La fuente trifásica del rotor se
convierte a bifásica por medio de la matriz de transformación de la ecuación (3.56) en un
marco de referencia fijo al estator, y es:
Figura 3- 15. Voltajes v qr , v dr & tiempo.
Los voltajes bifásicos del rotor tienen la misma amplitud que los voltajes trifásicos (17.96
V) y se encuentran defasados 90º eléctricos con una frecuencia de 1.68 Hz.
46
Capítulo 3
Motor de Inducción Doble Alimentado
Corrientes, par electromagnético, posición y velocidad
Continuando con el modelo bifásico en la simulación para obtener las gráficas de
corrientes, velocidad, posición y par electromagnético se utilizan las ecuaciones de voltaje
(ecuación (2.43)) y la matriz de enlaces de flujo del modelo bifásico en un marco de
referencia fijo al estator; así como, la ecuación de la posición angular (2.13) y la ecuación
del par electromagnético (ecuación (2.14) y (2.36).
Las figuras 3-16 y 3-17, muestran las gráficas de las corrientes de estator y rotor en el
marco de referencia fijo al estator:
Figura 3- 16. Corrientes i qs , i ds del estator &tiempo.
Las componentes i qs , i ds de la corriente del estator se encuentran defasadas 90º eléctricos,
y tienen una frecuencia de 60 Hz, que corresponde a la frecuencia de los voltajes de la
fuente de alimentación del estator.
Figura 3- 17. Corrientes i qr , i dr del rotor &tiempo.
47
Capítulo 3
Motor de Inducción Doble Alimentado
Las componentes directo y en cuadratura ( i qr , i dr ) de la corriente del rotor presentan las
mismas características, se encuentran defasadas 90º, a 60 Hz .
Las corrientes del estator y rotor presentan un transitorio de 0.45 segundos,
aproximadamente, estabilizándose después de estos segundos a una amplitud de 8
amperes.
Transformado las corrientes bifásicas a trifásicas por medio de la ecuación (2.19) que es la
inversa de la matriz de transformación. Las corrientes trifásicas del estator se muestran
en la siguiente figura:
Figura 3- 18. Corrientes trifásicas el estator.
Las corrientes en el estator muestran un transitorio durante 0.45 segundos
aproximadamente, después de estabilizarse tienden a una amplitud pico 8 Amperes.
Dichas corrientes están desfasadas 120º eléctricos entre sí a una frecuencia de 60 Hz.
La figura 3-19 muestra las corrientes trifásicas del rotor:
Figura 3- 19.. Corrientes trifásicas del rotor.
48
Capítulo 3
Motor de Inducción Doble Alimentado
Después de un transitorio de 0.45 segundos las corrientes del rotor se estabilizan con una
amplitud de 8 amperes, con una frecuencia de 1.8 Hz.
Por ultimo, en las figuras 3-20 y 3-21 se muestran el subsistema mecánico, es decir las
gráficas de la velocidad mecánica del rotor, posición y el par electromagnético:
Figura 3- 20. Velocidad mecánica y posición del rotor.
La figura 3-20 muestra la gráfica de la velocidad mecánica del rotor y tiende a un valor
constante después de 0.5 segundos aproximadamente. Así, la velocidad tiende a su valor
nominal (183 rad/seg).
Al igual que en la gráfica de la velocidad del rotor, la gráfica de la posición muestra una
pendiente constante a partir de 0.5 segundos, y es lo que se espera ya que la derivada de la
posición es igual a la velocidad multiplicada por el número de polos (ecuación (2.14)).
Figura 3- 21. Par electromagnético.
49
Capítulo 3
Motor de Inducción Doble Alimentado
La figura 3-21 muestra una etapa transitoria con oscilaciones. La etapa transitoria se
estabiliza después de 0.5 segundos aproximadamente, para luego tener un valor constante
de 9 N-m en estado estacionario. Este valor constante es igual al del par de carga, esto se
debe a que se tiene un par de fricción viscosa igual a cero ( β = 0 ) y además en estado
estacionario la derivada de la velocidad es cero, y por lo tanto τ em = τ L .
Conclusiones
La máquina de inducción doble alimentada (MIDA), está formada por una máquina de
inducción de rotor devanado. Se caracteriza porque tiene su estator conectado a una
fuente de alimentación de frecuencia constante y su rotor conectado a un convertidor
estático bidireccional.
El control para un motor de inducción doble alimentado se coloca del lado del rotor por lo
que fue necesario establecer la dirección los flujos de las potencias, así como sus signos
(sección 3.1), que se tendrá como base en el desarrollo de la tesis. De esta sección se
concluyó con una tabla comparativa (tabla 3-2) de los modos motor y generador a
velocidades sub-síncrona y super-síncrona, en la cual se pueden apreciar los signos de las
potencias en cada caso. Como el objetivo de la tesis es trabajar en modo motor, en ambos
casos (velocidad sub y super-síncrona) la potencia del estator ( Ps ), es entrante. La potencia
mecánica Pm , siempre será saliente y la potencia del rotor Pr , solo será saliente a
velocidades sub-síncrona y entrante a velocidades super-síncrona.
Lo más sobresaliente del análisis en estado estacionario es la obtención de
electromagnéticos y son:
3 pares
1) El par asíncrono constante τ s para un deslizamiento dado, producido por el voltaje
suministrado al estator v1 (figura 3-7). Esté par actúa como par-motor en
operación sub-síncrona es decir en el intervalo de 0 < s < 1 y como par-regenerador
en operación super-síncrona − 1 < s < 0 .
2) Par asíncrono constante τ r para un deslizamiento dado, producido por el voltaje
aplicado al rotor ( v 2 ) (figura 3-8). El par actúa como par-regenerador en ambas
operaciones sub y super-síncrona.
3) Par producido por la interacción de los campos del estator y rotor ( τ sr ) (figura 3-9).
El par se produce por la interacción de ambos campos, se observa que en operación
sub-síncrona se tiene un par regenerador, y en modo super-síncrona un par motor.
50
Capítulo 3
Motor de Inducción Doble Alimentado
4) Par total es la suma de los tres pares descritos anteriormente y en operación subsíncrona produce un par-motor y un par-regenerador en operación super-síncrona
(figura 3-10).
A diferencia del motor de inducción jaula de ardilla, del cual solo se obtiene un par
electromagnético, el MIDA presenta estos tres pares debido a la alimentación del lado del
estator y rotor.
El MIDA puede operar en modo motor a velocidades sub-síncronas (por debajo de la
velocidad de síncronismo) y super-síncronas (por encima de la velocidad de síncronismo),
así del par total se obtiene información de cómo será el comportamiento de la máquina de
inducción en configuración doble alimentada.
En el MIDA, una forma de saber en qué modo de operación está la máquina es a través
del signo del par electromagnético. Si es positivo la máquina está en modo motor y en caso
contrario (negativo) se estará trabajando en modo generador. Del par total obtenido en la
del análisis en estado estacionario, se concluye que es un par electromagnético positivo
por lo que se está en modo motor, que es el modo de operación que se utiliza en el
desarrollo de este trabajo.
Para el modelado de la máquina de inducción trifásica se debe tomar en cuenta que en
condiciones normales de operación, los circuitos eléctricos son balanceados y simétricos.
Se concluye la primera fase del trabajo de tesis con la simulación del modelado del MIDA
se realiza en lazo abierto en un marco de referencia fijo al estator, mediante la simulación
en MATLAB/Simulink.
Una forma de comprobar que el sistema funcionará de manera correcta, fue cortocircuitar
al rotor, es decir, poner los voltajes bifásicos del rotor igual a cero. Obteniendo, de esta
manera, el modelo de un motor jaula de ardilla y se comprobaron los resultados de las
graficas de las corrientes del estator y rotor, la velocidad, par electromagnético con las
presentadas en [11], [12] y [15].
51
CAPÍTULO 4
ESTRATEGIAS DE CONTROL DE LA MÁQUINA DE INDUCCIÓN
DE ROTOR DEVANADO
INTRODUCCIÓN
En el control de la máquina de inducción se desea controlar dos magnitudes no accesibles
directamente, que son:
• El par
• El flujo en el entrehierro
El control del par es necesario ya que si se detecta un error en la velocidad mecánica
deseada, se ha de variar el par obtenido para que la máquina regrese a la operación
óptima. El valor máximo del par proporcionado por la máquina está limitado (se indica
con una saturación en los esquemas de control) normalmente por la potencia que puede
dar el convertidor. En realidad la limitación está en el valor máximo de la intensidad que
éste puede dar.
El control del flujo es necesario para evitar que la máquina entre en la zona de saturación
con lo que el modelo lineal que se utiliza deja de ser válido y la estimación o cálculo del
par deja de ser correcto. Normalmente se fija un valor de flujo o intensidad magnetizante,
en el inicio de la curva de saturación, que es el punto de trabajo nominal. En el caso en que
se desea trabajar con velocidades de la máquina superiores a la nominal, se entra en la
zona denominada “debilitamiento de campo” [19], donde se disminuye el flujo o
intensidad magnetizante para evitar que los voltajes inducidos en los devanados del
motor superen sus valores nominales.
4.1 Métodos clásicos de control del motor de inducción de rotor devanado
(MIRD )
4.1.1
Formas de control de velocidad del MIRD
La velocidad de un MIRD puede ser controlada colocando 3 resistores variables externos
en el circuito del rotor a través de los anillos rozantes [1], [17], como se indica en la figura
4-1.
53
Capítulo 4
Generalidades sobre el Control Vectorial
Figura 4- 1. Motor de inducción de rotor devanado y resistencias adicionales en el rotor.
Si la barra cortocircuitadora indicada en la figura 4-2 se mueve hacia el extremo derecho,
en cada fase del rotor conectado en estrella se inserta una resistencia de rotor máxima.
Cuando se mueve al extremo izquierdo, se introduce una resistencia externa al rotor
mínima o nula que representa la resistencia equivalente de un rotor jaula de ardilla.
B arra
puenteadora
L1
T1
L2
T2
T3
S3
S2
A lim entación
de c.a.
trifásica
S1
M1
M2
R r creRr
decre- ciente
ciente
M3
L3
E stator
(estrella o triángulo)
R otor
(estrella)
A nillos
rozantes
R esistencia del rotor
(estrella)
Figura 4- 2. Esquemático de los devanados del MIRD con resistencias externas.
La figura 4-3 muestra las características del funcionamiento con la resistencia externa
agregada al circuito del rotor. La zona de funcionamiento entre vacío y plena carga está
comprendida entre par cero y par nominal. Las curvas indican que el deslizamiento es
proporcional a la magnitud de la resistencia añadida al rotor. Cuanto mayor sea la
resistencia añadida al rotor, peor será la regulación de velocidad del motor, esto se debe a
que al variar la resistencia del rotor, la curva del par sufre un deslizamiento hacia valores
decrecientes de en velocidad, con forma aumenta la resistencia [1, p. 366]. Por
consiguiente, es posible variar la velocidad de un motor de rotor devanado con carga
hasta cualquier valor por debajo de la velocidad síncrona ( ηs ), añadiendo o quitando
resistencia al rotor. Como resultado, la resistencia de arranque proporciona:
(1) pares de arranque elevados, y
(2) corrientes de arranque reducidas.
(3) También sirve como medio para controlar la velocidad para velocidades por debajo
de la de sincronismo.
54
Capítulo 4
Generalidades sobre el Control Vectorial
η = η s (1 − s )
Figura 4- 3. Variación de velocidad en un MIRD con resistencia variable en el rotor.
En la figura 4-3 se representa a la resistencia variable como R ex y conforme aumenta su
valor la nueva representación se muestra a través de las variables R ex1 K R ex 4 .
Este método incrementa el par de arranque, en tanto que limita la corriente de arranque.
Sin embargo, es un método ineficiente porque generalmente las resistencias no son iguales
y existen desequilibrios en los voltajes y corrientes.
Otra forma para controlar la velocidad del rotor es conectar un puente rectificador trifásico
en las terminales del rotor y alimentar la potencia rectificada en un solo resistor variable
[9]. El resultado de la curva característica par-velocidad es idéntico a la obtenida con un
reóstato trifásico; desafortunadamente, el reóstato aun tiene que variarse mecánicamente
con el propósito de cambiar la velocidad.
Se puede hacer un control totalmente electrónico como se observa en la figura 4-4.
Agregando un chopper y un resistor fijo Ro al circuito secundario. En este circuito, el
capacitor C suministra los pulsos altos de corriente trozados por el chopper. Variando el
chopper en el tiempo de encendido t0, la resistencia aparente en el puente rectificador
puede ser alta o baja. La relación está dada por:
Rd =
donde:
Rd
D
(4. 1)
R0
D2
es la resistencia aparente entre A1 y A2
es el ciclo de trabajo del chopper.
ROTOR
ESTATOR
Rectificador
IR
1
Línea
trifásica
2
3
E
Troceador
L
A1
A
B
N
Io
Id
C
Ed
D
Ro
Eo
C
A2
Figura 4- 4. Control de velocidad de un MIRD usando un resistor de carga y un chopper.
55
Capítulo 4
Generalidades sobre el Control Vectorial
La desventaja de los métodos anteriores es que la potencia del rotor se disipa en el resistor
en forma de calor.
4.1.2
Recuperación de potencia en un MIRD
En lugar de disipar la potencia en el rotor con una resistencia, se podría usar esta potencia
para cargar una batería grande de corriente directa (figura 4-5). Asumiendo que el voltaje
E2 de la batería puede variar desde cero a algún valor máximo arbitrario. El voltaje E
(corriente alterna) en las terminales del rotor es:
E = sE oc
donde:
s
Eoc
(4. 2)
es el deslizamiento, y
es el voltaje del rotor a circuito abierto.
Por otro lado, el voltaje de salida rectificado Ed es:
E d = 1.35E
(4. 3)
Despejando el deslizamiento de la ecuación (4.2) y sustituyendo E de la ecuación (4.3) en la
ecuación (4.2), se tiene:
s=
(4. 4)
Ed
1.35E oc
Debido a que la caída de voltaje en el inductor es despreciable, Ed =E2
s=
(4. 5)
E2
1.35 Eoc
ROTOR
ESTATOR
Id
Rectificador
IR
1
Línea
trifásica
2
+
E
3
+
A
B
N
L1
E2
Ed
C
-
-
Figura 4- 5. Control de velocidad usando una batería de voltaje variable.
Reconociendo que EOC es una cantidad fija, la ecuación muestra que el deslizamiento
depende exclusivamente del voltaje E2 de la batería. En consecuencia, podemos variar la
velocidad desde velocidad síncrona (s=0) a cero (s=1) variando el voltaje de la batería
desde cero a 1.35EOC.
En la práctica, en lugar de cargar una batería para absorber la potencia del rotor, usamos
un inversor trifásico que regrese la potencia a la fuente de ca. El inversor conmutado se
conecta al mismo alimentador que suministra potencia al estator (figura 4-6). Se agrega un
transformador T, para que el valor efectivo de ET este entre 80 y 90 % de E2.
56
Capítulo 4
Generalidades sobre el Control Vectorial
1
Línea
trifásica
2
3
ROTOR
ESTATOR
Id
Rectificador
IR
+
E
+
A
B
N
Inversor
L1
E2
Ed
T
ET
C
-
-
Procesador de
disparo de
compuerta
Velocidad deseada
Velocidad actual
Figura 4- 6. Control de velocidad usando un rectificador y un inversor conmutado naturalmente.
donde
E 2 es el voltaje de corriente directa dado por el inversor, y
E T es el voltaje del devanado secundario del transformador.
Este método de control de velocidad es muy eficiente porque la potencia del rotor no se
disipa en un grupo de resistores, sino que se regresa a la línea. Otra ventaja es que para
cualquier ET, la velocidad es prácticamente constante desde sin carga hasta plena carga [9].
Aunque los motores de inducción tienen una estructura simple, su modelo matemático es
complejo debido al grado de acoplamiento entre un gran número de variables y el
comportamiento no lineal de las mismas.
La teoría del control vectorial o campo orientado (FOC, field oriented control) es un
método comúnmente utilizado en el control de máquinas de corriente alterna (ca) ya que
esencialmente, transforma la estructura dinámica de la máquina de ca en una estructura
equivalente a la del motor de corriente directa (cd) de excitación separada.
4.2 Introducción al control vectorial
Aún con las ventajas que ofrecen los motores de inducción sobre los de corriente directa
entre las cuales se encuentran: menor costo, menor volumen, tamaño y peso, mayores
niveles de voltaje, mayor eficiencia, menores niveles de ruido, menor mantenimiento y la
posibilidad de utilización en cualquier tipo de medio [17], su modelo matemático es
complejo debido a que los mismos presentan los siguientes inconvenientes [3]:
1. Estructura de control no lineal que da lugar a ecuaciones matemáticas complejas las
cuales hacen difícil la programación de algoritmos de control.
2. Variación de parámetros eléctricos debido a incrementos de temperatura.
3. Control multivariable, es decir, dependiente de varias condiciones simultáneamente.
57
Capítulo 4
Generalidades sobre el Control Vectorial
4. Alto grado de acoplamiento entre el flujo magnético y el par, a diferencia de los motores
de cd, donde estos dos vectores al ser ortogonales están perfectamente
desacoplados, facilitando su control.
El control vectorial o por campo orientado (FOC: Field Oriented Control), ha ofrecido
soluciones a los problemas anteriores mediante modelos y ecuaciones que permiten
obtener un comportamiento dinámico del motor de inducción similar al de un motor de
cd. La desventaja del FOC es que linealiza parcialmente el sistema (ya que la velocidad del
rotor está solo asintóticamente desacoplada del flujo rotórico) y por lo tanto deben
implementarse diferentes técnicas de control no lineal para mejorar el FOC, tales como
linealización de entrada/salida o linealización por retroalimentación [2].
El control vectorial se basa en reescribir las ecuaciones dinámicas de la máquina de
inducción en un marco de referencia que se orienta según el flujo (vector de flujo) que
puede ser: al flujo del estator, al flujo del rotor o al de magnetización de tal manera que en
el nuevo marco de referencia aparece una relación lineal entre la variable de control y la
velocidad.
(τ em )
La expresión par electromagnético
de la máquina de inducción es similar a la
expresión para el par electromagnético producido por una máquina de cd de excitación
separada. Esta analogía sirve como base para las diferentes formas de control vectorial,
donde el control del par de una máquina de ca es similar al control del par de la máquina
de cd.
Las corrientes estatóricas de la máquina de inducción pueden separarse en una
componente que produce el flujo y otra componente que produce el par, mediante
transformaciones que se explicarán en la siguiente sección, donde la implementación
vectorial requiere de la información del módulo y el ángulo del fasor de flujo estatórico,
rotórico o de magnetización, según hacia donde esté orientado el control.
La figura 4-7 muestra la analogía entre la estructura de una máquina de cd y el control
vectorial de una máquina de inducción.
Ia
If
τ em = K t Ia If
C o m p o ne nte
d el pa r
E n u n m arco
d e re fe re n cia
sín cro n o
i*
i*
In v e rs o r y
c o n tro la d o r
sd
C o m p o ne nte de flu jo
m o to r d e
in d u c c ió n
sq
τ e m = K t I sq I sd
C o m p o ne nte
d el pa r
C o m p o ne nte de flu jo
Figura 4- 7. Analogía entre el motor de cd y el control vectorial del motor de inducción.
58
Capítulo 4
Generalidades sobre el Control Vectorial
La expresión de par electromagnético en una máquina de cd., despreciando el efecto de
saturación y de reacción de armadura está dada por:
τ em = K t ⋅ I a ⋅ I f
donde:
Ia
If
Kt
(4. 6)
es la corriente de armadura,
la corriente para el devanado de campo y
es una constante de proporcionalidad
Las variables Ia e If son las variables de control en una máquina de corriente directa y
pueden ser consideradas como vectores ortogonales o desacoplados. En condiciones
normales, la corriente If se mantiene constante e igual a su valor nominal, por lo que el par
será proporcional a la corriente de armadura Ia. De esta forma existe un desacople entre If,
que representa el flujo magnético e Ia que representa el par.
En un motor de inducción, sin embargo, estos dos vectores están fuertemente acoplados
(no ortogonales). En un marco de referencia bifásico q,d, que gira a la velocidad síncrona ,
las componentes de corriente obtenidas (isq, isd), son las componentes de corriente del
estator, en los ejes directo y de cuadratura respectivamente. Si la componente de corriente
isq, se hace coincidir en fase con el flujo magnético del rotor (o del estator o de
magnetización) o con la componente de corriente que lo genera, se puede establecer una
analogía entre la componente isq en coordenadas de campo y la corriente de campo (If) en
el motor de cd, así como entre la componente isd y la corriente de armadura (Ia). De esta
forma el par en una máquina de inducción se puede expresar como:
τ em = K t ⋅ i sq ⋅ i sd
(4. 7)
Por lo que, manteniendo el flujo magnético isq constante, se puede realizar el control del
par del motor, mediante la corriente isd, ya que ambos vectores son ortogonales y están por
lo tanto desacoplados, pudiéndose variarlos independientemente sin afectar la
componente ortogonal.
4.3 Transformaciones de marcos de referencia orientados según el campo
Considerando el marco de referencia fijo a alguno de los fasores de flujo (rotórico,
estatórico o magnetización) se logra que la expresión del par electromagnético sea similar
al producido por una máquina de cd con excitación separada [2].
En la siguiente figura se presenta un marco de referencia general (x , y ) para cualquier
( )
fasor de flujo, denominándolo fasor de flujo general ψ sg el cual representa el fasor de
flujo rotórico, estatórico o magnetización y gira a velocidad ω g = dρ g dt .
59
Capítulo 4
Generalidades sobre el Control Vectorial
y
rβ sQ
is
ωg
ir
αs
α' r
x
αr
ρg
rα
θr
sD
Figura 4- 8. Marco de referencia general.
donde las fases sD y sQ representan las fases del estator y rα, rβ son las fases del rotor.
La fase rα del rotor está desplazada con respecto a la fase sD del estator en un ángulo θ r ,
como se muestra en la figura 4-8. Los fasores i s e i r (de la misma figura) son las corrientes
del estator y rotor respectivamente. Una forma
de identificar a las fases es
denominandolas como componente directa ( sD ) y componente en cuadratura ( sQ ).
La expresión del par electromagnético ( τ em ) es similar en todos los marcos de referencia.
La magnitud del par no se altera en los diferentes marcos, ya que no se altera el ángulo
entre los fasores de flujo y corriente. El par puede tomar las siguientes formas [2, p. 43]:
τ em =
τ em =
3P
(ψ mx i sy − ψ my i sx )
22
(4. 8)
3 P Lm
(ψ rx i sy − ψ ry i sx )

2 2  Lr

(4. 9)
3P
(ψ sx i sy − ψ sy i sx )
22
(4. 10)
τ em =
Así, el par electromagnético es proporcional al producto de una componente de corriente
que produce el flujo y otra componente de corriente, en cuadratura.
El par máximo se obtiene cuando el ángulo entre el flujo y la corriente es 90º
cuando los fasores están en cuadratura.
60
(π 2) , o sea
Capítulo 4
4.3.1
Generalidades sobre el Control Vectorial
'
Marco de referencia orientado al flujo del rotor ( ψ r )
La transformación de un sistema de referencia a otro sólo implica una rotación de todos
los fasores en un mismo ángulo ρ . En este caso, como está orientado al flujo del rotor, el
marco de referencia está girando a velocidad ω mr (ω mr =
d
dt
ρ r ) , como se observa en la
siguiente figura:
sQ
ωmr
y
x
ψ'r
i sy
ρr
sD
i sD
Figura 4- 9. Marco de referencia orientado al flujo del rotor(x,y).
(
La figura 4-9, involucra la transformación del fasor de corriente i D , i Q
(
)
) y del fasor de
enlaces de flujo ψ D , ψ Q , en el marco de referencia fijo al estator a fasores de corriente
(i
x
, i y ) y enlaces de flujo (ψ x , ψ y ) , en un marco de referencia (x,y) que gira en
sincronismo con el flujo del rotor,.
La siguiente figura muestra una proyección de la representación polar del vector del flujo
rotórico, que inicialmente se encuentra en un marco de referencia fijo al estator y girará en
un marco de referencia orientado al flujo del rotor.
→
ψ'r
ρr
ψrD
ψrQ
D
Figura 4- 10. Fasor de flujo del rotor.
Expresando el flujo del rotor en forma polar:
→'
→
ψ r = ψ r ∠ρ r .
donde:
→
| ψ r | es la magnitud del flujo del rotor,
ρr
es el ángulo del flujo del rotor.
61
(4. 11)
Capítulo 4
y
Generalidades sobre el Control Vectorial
cos ρ r =
ψ rD
→
| ψr |
sin ρ r =
;
ψ rQ
→
;
→
(4. 12)
ψ r = ψ 2rD + ψ 2rQ .
| ψr |
A continuación se presenta el cambio de coordenadas que se necesita para referir las
variables del marco de referencia fijo al estator al marco de referencia orientado al flujo del
rotor.
x
Q
y
ρ
D
ρ
Figura 4- 11. Transformación de las variables en el MR ‘D,Q’ a variables en el MR ‘x,y’.
La representación trigonométrica en forma matricial de la figura (4-11),
componentes del fasor de enlaces de flujo del rotor es:
ψ rx   cos ρ r
ψ  = 
 ry  − sin ρ r
sin ρ r  ψ rD 
⋅
.
cos ρ r  ψ rQ 
para las
(4. 13)
Desarrollando la primera fila ( ψ rx ) de la matriz de la ecuación (4.13), y sustituyendo las
ecuaciones expresadas en (4.12), se tiene:
ψ rx =
ψ rD
→
ψr
⋅ ψ rD +
ψ rQ
→
ψr
⋅ ψ rQ
(4. 14)
→ 2
ψ rx =
ψr
→
ψr
→
= ψr
de la segunda fila de la matriz expresada en (4.13), y sustituyendo las ecuaciones de(4.12),
se tiene:
ψ ry = −
ψ rQ
→
ψr
⋅ ψ rD +
62
ψ rD
→
ψr
⋅ ψ rQ
(4. 15)
Capítulo 4
Generalidades sobre el Control Vectorial
ψ ry = 0
→'
Se concluye que en esté marco de referencia el eje x, es coaxial al fasor ψ r , teniendo como
→
magnitud ψ r y un ángulo de cero grados, debido a la nueva orientación. Como se ve en la
ecuación (4.14) la componente directa (ψ rx ) del flujo rotórico en el eje x es igual a la
magnitud del flujo rotórico.
Como la corriente de magnetización del rotor es proporcional al flujo rotórico, se puede
hacer una analogía para el fasor de la corriente de magnetización del rotor:
→
→
(4. 16)
i mr = i mr ∠0 0 = i mr .
Por conveniencia en la manipulación de las variables se utiliza la siguiente notación:
→'
→
ψ r = ψ r = ψ rx ,
→
(4. 17)
→
i mr = i mr = i mr .
→'
→
donde se expresa que es el modulo del fasor ( ψ r ó i mr ) con un ángulo de cero grados a
menos que se especifique lo contrario. Está notación se utilizará en las siguientes
subsecciones.
Con la siguiente figura se concluye que este marco de referencia el eje x, es coaxial al fasor
del flujo rotórico:
sQ
i sQ
y
i s , i sψr
→
=
ψ'r
→
i sy
i sx
i
ψ
r
→
mr
=i
=
ψ
rx
x
mr
ρr
i sD
sD
Figura 4- 12. Componentes en cuadratura según el marco de referencia orientado al flujo del rotor.
Si se expresa el par como en la ecuación (3.9), considerando nula la componente en
cuadratura del flujo rotórico en el eje y:
63
Capítulo 4
Generalidades sobre el Control Vectorial
τ em =
3 P Lm
(ψ rx i sy )

2 2  Lr

(4. 18)
Expresando este par en función de alguna corriente que esté en cuadratura con i sy (figura
→
→
4.13), teniendo en cuenta que ψ 'r = L m ⋅ i mr , entonces:
τ em
donde
3 P  L2m
(i mr i sy )
=

2 2  Lr

(4. 19)
→
i mr = i mr
sQ
y
i mr
i sy
ρr
x
sD
Figura 4- 13. Componentes de corriente que producen el par.
De donde surge que el par expresado en el control orientado al flujo rotórico, es
proporcional al producto de una componente de corriente i mr , que produce el flujo, y otra
componente de corriente en cuadratura i sy , que produce el par.
En general la máquina de inducción se considera bajo condiciones magnéticas lineales, es
→
decir que i mr = i mr se mantiene constante. La estrategia de control es análoga a la de la
máquina de cd cuando se mantiene la corriente de campo constante y sólo se varía la
corriente de armadura.
→'
Marco de referencia orientado al flujo del estator (ψ s )
4.3.2
La siguiente figura muestra el cambio de variable, de un marco de referencia fijo a un
marco orientado al flujo estatórico. Ahora el marco de referencia gira a velocidad ω ms
(ωms
=
d
dt
ρs )
64
Capítulo 4
Generalidades sobre el Control Vectorial
sQ
is
isQ
y
ωs
ψs
=
ψ' s →
i sy
ρs
i sx
→
'
i ms
x
=ψ s
s
= im
i sD
=im
s
x
sD
Figura 4- 14. Componentes en cuadratura según el marco de referencia orientado al flujo del estator.
→
donde:
(4. 20)
→
ψ s' = ψ s ∠ρ s
En forma matricial, la transformación para el fasor de corrientes en el marco de referencia
(x,y) es:
i sx   cos ρ s
i  = 
 sy  − sin ρ s
sin ρ s  i sD 
 
cos ρ s  i sQ 
(4. 21)
Haciendo una analogía con la orientación al flujo rotórico, el eje x es coaxial con el fasor
→
'
s
→
ψ = ψ s = ψ sx y donde ψ sy = 0 , observe la figura 3-14.
A partir de la ecuación (3.10) el par es:
τ em =
3P
(ψ sx i sy )
22
(4. 22)
y además, si los devanados del estator y rotor el mismo número de vueltas efectivas, el
→
flujo magnetizante de acoplamiento es ψ s = L m ⋅ i ms . Sustituyendo está expresión en la
ecuación (4.20), el par resulta:
τ em =
→
→
donde i ms = i ms
→
3P

L
⋅
i
m
ms ⋅ i sy 

22

(4. 23)
es el módulo de la componente de corriente que produce el flujo
estatórico e i sy es la componente de corriente que produce el par. Si se mantiene el flujo
estatórico constante es posible controlar el par de la máquina variando solo la componente
i sy .
65
Capítulo 4
Generalidades sobre el Control Vectorial
La figura 4-15 muestra las componentes de corriente que producen el par en la
configuración de control orientado al flujo del estator.
sQ
y
x
i ms
i sy
ρs
sD
Figura 4- 15. Componentes de corriente que producen el par.
4.3.3
'
Marco de referencia orientado al flujo de Magnetización ( ψ m )
El marco de referencia fijo (x,y) girará a la velocidad ω m =
d
dt
ρ m , como se muestra en la
siguiente figura.
sQ
ωm
y
x
ψ' m
i sy
ρm
sD
Figura 4- 16. Marco de referencia orientado al flujo de magnetización (x,y).
→
→
→
→
el flujo de magnetización es ψ 'm = ψ m ∠ρ m y además se cumple que ψ 'm = L m ⋅ i m , si se
considera a L m constante.
Podemos expresar en forma matricial la transformación de cambio de marco de referencia
(igual que los casos anteriores sólo que estará girando con un ángulo ρ m ) como:
i sx   cos ρ m
i  = 
 sy  − sin ρ m
sin ρ m  i sD 
 
cos ρ m  i sQ 
(4. 24)
Haciendo una analogía con en el marco de referencia orientado al flujo del rotor , el eje x es
coaxial con el fasor del flujo de magnetización y utilizando la notación de la ecuación
'
(4.17). El fasor del flujo de magnetización es ψ m = ψ m = ψ mx y a la corriente de
→
→
magnetización i 'm = i m = i mx , donde ψ my = 0 e i my = 0 (figura 4-17).
66
Capítulo 4
Generalidades sobre el Control Vectorial
sQ
is
isQ
y
→
→
'
ψ
m
m
=ψ
→
→
'
i
i sx
=ψ
im
=
im
mx
x
= im
x
sy
ρm
isD
sD
Figura 4- 17. Componentes en cuadratura según el marco de referencia orientado al flujo de magnetización.
Considerando la ecuación (4.8), el par es:
τ em =
→
3P
(ψ mx i sy ),
22
(4. 25)
→
recordando que ψ 'm = L m ⋅ i m , el par resulta:
τ em =
3P
L m i mx i sy .
22
(4. 26)
Se concluye que el par expresado en el marco de referencia orientado al flujo de
magnetización es proporcional al producto de una componente de corriente i mx que
produce el flujo principal y otra componente de corriente en cuadratura i sy que produce el
par.
4.4 Fundamentos de la implementación del Control Vectorial
En este trabajo se simplifica el modelo omitiendo el modelo del inversor, ya que se supone
que se generan las ondas de corriente o voltaje ideales (ia, ib, ic), que serán iguales a las
ondas de referencia correspondientes, generadas por el controlador.
Como se explicó anteriormente, para implementar el control por campo orientado, el
modelo del motor de inducción en un marco de referencia trifásico, se transforma a un
marco de referencia bifásico rotatorio, con ecuaciones más sencillas, que describen un
comportamiento análogo al de una máquina de corriente directa, facilitando
considerablemente el control del motor y mejorando su comportamiento dinámico.
Las transformaciones de planos coordenados se realizan tanto en forma directa (sistema
trifásico a bifásico rotatorio), como de forma inversa, para volver a obtener los valores de
corrientes de fase una vez realizado el control, como se muestra en la figura 4-18.
67
Capítulo 4
Generalidades sobre el Control Vectorial
CONTROL
MÁQUINA
INVERSOR
i *sq
i*sd
i*sα
q ,d
*
α , β i sβ
α ,β
a ,b ,c
ia*
ia
*
b
ib
ic*
ic
i
a ,b ,c
α ,β
i sα
i sβ
ρ
α ,β
q ,d
i sq
i sd
ρ
TRANSFORMACIÓN INVERSA
TRANSFORMACIÓN DIRECTA
Figura 4- 18. Transformación de planos de coordenadas.
Cada transformación se realiza en dos etapas:
1-) Transformación de las corrientes de fase trifásicas (ia, ib, ic), a un sistema bifásico
estacionario i sα , i sβ . (Transformada de Clarke [16]).
(
)
2-) Transformación del sistema anterior a un marco de referencia bifásico giratorio (isd, isq).
(Transformada de Park) [2], [12].
De igual forma las transformaciones de Clarke y Park inversas, tienen como objetivo
llevar los valores obtenidos en el plano imaginario d,q (isd*, isq*), que representan los
valores de par y flujo del rotor obtenidos producto del control, a un sistema de referencia
trifásico (ia*,ib*,ic*).
4.5 Método directo e indirecto de control por campo orientado
La implementación del control por orientación según el campo requiere de la información
del módulo y el ángulo del fasor de flujo estatórico, rotórico o de magnetización, según hacia
dónde esté orientado el control. Una vez seleccionado el marco de referencia fijo al fasor
de flujo correspondiente, se trabajan con las componentes de cuadratura de las variables
elegidas. Existen dos métodos de adquisición del módulo y ángulo, que son: directo e
indirecto [2], [16].
La diferencia fundamental entre ambos métodos es que en el caso del método directo se
calcula la magnitud del vector flujo del rotor, mientras el método indirecto se obtiene la
posición del vector de flujo sin necesidad de calcular su valor. A continuación se explican
las características, ventajas e inconvenientes de ambos métodos.
Método directo
El algoritmo del método directo requiere la medición o cálculo del vector flujo del
rotor. Existen varias formas de lograr lo anterior como son:
1- Colocación de sensores de flujo (sensores de efecto Hall) en el entrehierro.
68
Capítulo 4
Generalidades sobre el Control Vectorial
Esta medición permite obtener el vector corriente magnetizante ( i m ), que representa
el flujo en el entrehierro, el cual combinado con la señal de corriente en el estator
permite generar el vector corriente magnetizante modificada ( i mr ). Esta técnica tiene la
desventaja de requerir de una modificación en el motor de inducción para la
colocación de los sensores, además de que estos son frágiles y sensibles a los
cambios de temperatura y al ruido.
2- Colocación de bobinas en el estator.
Este método permite también la adquisición del vector i m y el cálculo del vector
i mr . Su principal inconveniente es que las bobinas no pueden ser utilizadas a
frecuencias menores de 1Hz, debido a los problemas que surgen con la integración
analógica, desvirtuando considerablemente la medición de la corriente de
magnetización a velocidades bajas.
3- Modelos de flujo.
Los modelos de flujo se basan en modelos matemáticos de estimación del flujo del
rotor a partir de señales más sencillas de medir como las corrientes de fase y la
velocidad del rotor. La utilización de modelos de flujo tiene la ventaja de que la
operación del motor es factible a velocidad cero ya que las ecuaciones son válidas
para ωm igual a cero.
La principal dificultad de este método es que las ecuaciones tienen en cuenta la
constante de tiempo del rotor τr, como una magnitud constante, no considerando
los cambios de la resistencia del rotor debido a la temperatura y a las variaciones
de la frecuencia del rotor (efecto skin), así como los cambios de inductancia debido
a los efectos de saturación, provocando que variaciones en la constante de tiempo,
lleven a la desorientación del flujo del rotor, lo cual constituye uno de los aspectos
más críticos del control por campo orientado. La solución a este problema radica en
la utilización de técnicas de “adaptación de parámetros en línea” que permitan con
el motor en funcionamiento, calcular la constante de tiempo del rotor de acuerdo a
los parámetros reales de operación del motor, en un momento dado.
En el método directo de campo orientado, es necesario realizar la medición o el
cálculo del vector flujo del rotor, y orientar el vector de la componente de corriente
del estator (isd) con el vector flujo del rotor.
Método indirecto
Los métodos indirectos tienen la ventaja de ser más simples de implementar, ya
que eliminan la necesidad de la medición o el cálculo computacional del vector
flujo del rotor. Estos métodos se le conocen como "sensorles" [16].
En la implementación del control vectorial para esté trabajo de tesis se utiliza el método
indirecto de control orientado al flujo del estator, porque se requiere que las potencias
activas y reactivas estén desacopladas para la recuperación de energía. Además, el
método asegura el desacoplamiento para el control apropiado de la amplitud y ángulo del
fasor de la corriente del rotor y tiene la ventaja de estabilizar al motor.
69
Capítulo 4
Generalidades sobre el Control Vectorial
Conclusiones
En el control de una máquina de inducción se deben conocer dos parámetros y son: el par
y el flujo en el entrehierro. El par es necesario cuando se detecta un error en la velocidad
mecánica deseada y el flujo en el entrehierro es necesario para evitar que la máquina entre
en la zona de saturación.
Existen varias técnicas para controlar al MIDA. En este trabajo se utiliza la técnica del
control vectorial por la ventaja que presenta en el desacoplamiento de las variables del
motor, permitiendo obtener un comportamiento dinámico similar al de un motor de cd.
El control vectorial se basa en reescribir las ecuaciones dinámicas de la máquina de
inducción en un marco de referencia que se orienta según flujo y puede ser orientado: al
flujo estatórico, al flujo rotórico o al de magnetización, de tal manera que en el nuevo
marco de referencia, aparece una relación lineal entre la variable de control y la velocidad.
En todos los marcos de referencia, la transformación de coordenadas se realiza ubicando el
eje x del marco de referencia, coaxialmente con el fasor de flujo del rotor, estator o de


→
→
→


magnetización  ψ r , ψ s , ψ m  , de tal forma que la expresión del par τ em resulta del
producto de dos corrientes en cuadratura (figura 4-16); Así, la expresión que modela a la
máquina de inducción resulta ser un control de las corrientes en forma independiente
como las expresiones de una máquina de cd con excitación independiente.
ψr
__
__
sQ
___
is
__
__
imr
ψs
i sy
i ms
isy
____
imr
ρs
corrientes que
producen par
ψm
i mx
sD
corrientes que
producen flujo
Figura 4- 19. Diagrama de las corrientes (directa y en cuadratura) orientadas a los distintos marcos de
referencia.
70
Capítulo 4
Generalidades sobre el Control Vectorial
La transformación de un marco de referencia a otro se realiza por medio de la matriz de
transformación denominada Transformada de Park [2],[12].
En la implementación del control por campo orientado se requiere de la información del
módulo y el ángulo del fasor de flujo estatórico, rotórico o de magnetización, según hacia
dónde esté orientado el control. Una vez seleccionado el marco de referencia fijo al fasor
de flujo correspondiente, se trabaja con las componentes de cuadratura de las variables
elegidas. Existen dos métodos de adquisición del módulo y ángulo, que son: directo e
indirecto.
En el desarrollo de este trabajo se utiliza el método indirecto ya que el módulo y el ángulo


→
→
→


del fasor de flujo  ψ r , ψ s , ψ m  , se obtienen a partir de las ecuaciones de las corriente del
estator y rotor, y de la velocidad del rotor. En el control directo, el módulo y ángulo del
fasor de flujo se miden directamente con sensores.
71
CAPÍTULO 5
CONTROL VECTORIAL APLICADO AL MIDA
INTRODUCCIÓN
Las máquinas eléctricas giratorias son las más utilizadas en la industria. Las bombas,
ventiladores, sopladores, etc, (motores en general) son responsables de aproximadamente
la mitad de la electricidad consumida por la industria [2].
Algunas de las aplicaciones más comunes, utilizando el motor de inducción de rotor
devanado en configuración doble alimentado son: bombas en el tratamiento de aguas
sucias, para circular agua, abastecimiento de agua, sopladores en la ventilación en minas,
etc. En este tipo de aplicaciones el par de carga es proporcional al cuadrado de la
velocidad, por lo que se tiene una limitación en el rango de control de velocidad. La
característica más importante de la configuración doble alimentado se denomina “slip
recovery system” y es que en lugar de disipar la potencia del rotor en los resistores en
forma de calor (métodos tradicionales) se regresa a la red de alimentación.
El control vectorial o control de campo orientado (FOC: Field Oriented Control) de un
motor de inducción permite mejorar su respuesta dinámica aproximándola a la del motor
de corriente directa (cd). Así como también desacopla las variables y se consigue por tanto
un control independiente de velocidad y par equiparables a la sencillez en el control del
motor de cd.
En esté capítulo se desarrolla un esquema de control de velocidad de un motor de
inducción doble alimentado (MIDA), mediante la técnica de control orientado al flujo
estatórico. Se utiliza el control orientado al flujo del estator, debido a que se requieren las
corrientes sinusoidales del estator y el desacoplamiento de las potencias activa y reactiva.
5.1 Control de campo orientado (FOC) del motor de inducción doble
alimentado (MIDA)
El MIDA en configuración doble alimentado permite operar el motor desde velocidades
mecánicas (del rotor) sub-síncrona hasta super-síncrona y viceversa.
El MIDA puede estar alimentado y controlado desde el estator o desde el rotor o desde
ambos [2], [10]. De las diferentes combinaciones posibles, el control del lado del rotor es la
73
Capítulo 5
FOC aplicado al MIDA
parte ventajosa ya que el convertidor de potencia sólo necesita manipular la potencia de
deslizamiento. La configuración física del MIDA se muestra en la figura 5-1.
∼
Transformador
Convertidor de flujo de
potencia bidireccional
MI
P s, Q s
θr
ira, irb, irc {
τem, isa, isb, isc {
Sistema de
control
Señales de referencia
Figura 5- 1. Configuración física de una MIDA
Debido a esta configuración, el sistema resulta muy atractivo para aquellas aplicaciones
donde el intervalo de velocidad está limitado y donde la recuperación de energía es un factor
dominante. Además, posibilita el control en forma desacoplada de las potencias activas y
reactivas generadas o absorbidas apoyándose, para esto, en técnicas de control vectorial o
Campo Orientado para el control de la corriente rotórica.
En este trabajo de tesis el modelo del convertidor es ideal, ya que se supone que se
generan las ondas de voltaje del rotor ( v ra , v rb , v rc ) senoidales, que serán iguales a las
ondas de referencia correspondientes a las generadas por el controlador.
5.1.1
Ecuaciones de control en un marco de referencia orientado al flujo del estator
En este trabajo se utiliza el control orientado al flujo del estator, debido a que se requieren las
corrientes sinusoidales del estator y el desacoplamiento de las potencias activa y reactiva.
Este tipo de control asegura el desacoplamiento requerido para el control apropiado de la
amplitud y ángulo de fase del fasor espacial de la corriente del rotor. Además, tiene la
ventaja de estabilizar al motor.
En el capítulo 4 se explicaron los diferentes marcos de referencias del control orientado
según campo y específicamente en la sección 4.3.2 se explicó el marco de referencia
orientado al flujo del estator.
En circuitos de corriente alterna, en donde las corrientes y tensiones varían senoidalmente
en el tiempo, es conveniente que estas magnitudes se representen por sus fasores
complejos, también denominados vectores espaciales.
74
Capítulo 5
FOC aplicado al MIDA
Ecuación del Par Electromagnético
El par electromagnético en el marco de referencia orientado al flujo del estator es
proporcional al producto del vector espacial de la corriente de magnetización del estator
→
( | i ms | ) y la componente i sy de la corriente del estator, que produce el par. Dicho par es:
τ em =
→
3P

⋅
L
i
m
ms ⋅ i sy 

22

(5. 1)
Así, se desea poner las ecuaciones de voltaje del estator y rotor en función del módulo de
la corriente de magnetización.
Ecuaciones de voltajes del MIDA
Utilizando la misma notación que en la sección 4.3.2 del capitulo 4, el vector espacial de
→
→
flujo del estator orientado al flujo estatórico es: ψ sψs = L m i ms . Despejando el módulo de
la corriente de magnetización, se tiene:
→
→
i ms =
ψ sψs
(5. 2)
Lm
donde L m es la inductancia de magnetización y, además, el vector espacial del flujo del
estator (ver detalles en [2] p. 44), orientado al flujo del estator es:
→
→
→
ψ sψs = L s i sψs + L m i rψs
(5. 3)
Sustituyendo la ecuación (5.3) en (5.2) y despejando el fasor espacial de la corriente del
estator orientado al flujo del estator, se tiene:
→
i sψs =
Lm
Ls
→
 →

−
i
i
rψs 
 ms


(5. 4)
Expresando la ecuación (5.4) en sus componentes (x,y), tenemos a las corrientes del estator
en función de las corrientes del rotor en el mismo marco de referencia
Lm
Ls
(5. 5)
 →

 i ms − i rx 


(5. 6)
i sy = −i ry
i sx =
Lm
Ls
Las ecuaciones de los fasores espaciales de voltaje del estator y rotor (detalles [2], p. 44)
orientados al flujo del estator son:
→
→
u sψs = R s i sψs + L s
d
dt
→
i sψs + L m
d
dt
75
→
→
→


i rψs + jω ms  L s i sψs + L m i rψs 


(5. 7)
Capítulo 5
FOC aplicado al MIDA
→
→
u rψs = R s i rψs + L r
d
dt
→
i rψs + L m
→
d
dt sψs
i
→
→


+ j(ω ms − ω r ) L r L rψs + L m i sψs 


(5. 8)
Del lado del estator
Sustituyendo la ecuación (5.4) en (5.7) se tiene:
R sLm
Ls
→
u sψs =
→
 →

−
i
i
ψs  + L m
ms
r



d
dt
→
→
i ms + jω ms L m i ms
(5. 9)
Agrupando del lado derecho los términos en función del módulo de la corriente de
magnetización, la ecuación anterior (5.9) se representa como:
Ts
donde:
Y
d
dt
→
→
→
i ms + i ms (1 + jω ms Ts ) = u sψs
→
Ls
+ i rψs
R sLm
(5. 10)
Ls
Rs
es la constante de tiempo del estator.
Ts =
Ts
ω ms es la velocidad angular del marco de referencia orientado al flujo del estator.
Expresando la ecuación (5.10) en sus dos componentes (directo “x” y de cuadratura “y”),
se tiene:
Ts
d
dt
→
→
i ms + i ms =
→
ω ms Ts i ms =
Ls
u sx + i rx ,
R sLm
Ls
u sy + i ry .
R sLm
(5. 11)
(5. 12)
Para el motor de inducción doble alimentado (MIDA), se asume una fuente trifásica
simétrica senoidal, con frecuencia ωs .
Del lado del rotor
sustituyendo la ecuación (5.4) en (5.8), se tiene:
→
→
u rψs = R r i rψs + L r
d
dt
→
i rψs +
L2m
Ls
d
dt
→
→
→ 

L2m  →
 →


(
)
−
+
ω
−
ω
+
i
i
j
L
i
 i ms − i rψs  (5. 13)
rψs 
ms
r  r rψs
 ms
Ls 




La ecuación anterior (fasor espacial de voltaje de rotor orientado al flujo estatórico), se
expresa como:
→
[
u rψs = R r + L' r
d
dt
]i
→
rψs +
L2m
Ls
d
dt
→
→

L2 → 
i ms + jωsl L'r i rψs + m i ms 
Ls


76
(5. 14)
Capítulo 5
donde:
y
FOC aplicado al MIDA
L'r = L r −
L2m
,
Ls
ωsl = ω ms − ω r .
ω es la velocidad de deslizamiento,
sl
ω ms es la velocidad del marco de referencia,
ωr
es la velocidad mecánica del rotor.
Dividiendo a la ecuación (5.13) entre R r y agrupando del lado izquierdo de la ecuación al
fasor espacial de corriente del rotor, se tiene:
→
Tr'
donde:
d
dt
→
→
i rψs + i rψs =
u rψs
(
)
→
→
 →

− jωsl Tr' i rψs − Tr − Tr'  dtd i ms + jωsl i ms 
Rr


(5. 15)
Tr' = σ rTr ,
L2m
σr = 1 −
,
Lr Ls
Lr
.
Rr
y Tr es la constante de tiempo del rotor.
Tr =
Expresando la ecuación (5.15) en sus componentes directo y de cuadratura (x,y):
Tr'
Tr'
d
dt
d
dt
i rx + i rx =
i ry + i ry =
u rx
+ Tr' ωsl i ry − Tr − Tr'
Rr
[
]
u ry
[
]
Rr
d
dt
→
i ms
(5. 16)
→
− Tr' ωsl i rx − Tr − Tr' ωsl i ms
(5. 17)
Las ecuaciones (5.16) y (5.17) tienen términos acoplados no deseados entre los ejes x,y del
circuito del rotor ( i rx , i ry ). Estos términos pueden eliminarse utilizando las siguientes
componentes de voltajes desacoplados, las cuales se obtienen al asumir constante el flujo
→
de estator y por consiguiente la corriente de magnetización ( | i ms | ) es constante.
u drx = −ωsl L' r i ry
(
(5. 18)
)
→
u dry = ωsl L'r i rx + ωsl L r − L'r i ms
(5. 19)
Estas ecuaciones se agregan a las salidas del controlador de corriente, las cuales controlan
las corrientes i rx e i ry del rotor.
77
Capítulo 5
5.1.2
FOC aplicado al MIDA
Condiciones del FOC
En el marco de referencia orientado al flujo del estator las componentes de la corriente del
rotor i rx , i ry corresponden directamente a las componentes de la corriente del estator
(i
sx
( )
) expresadas en dicho marco de referencia.
, i sy
De la ecuación (5.5) se estableció que la corriente i ry del rotor es proporcional a la
componente i sy de la corriente del estator y se usa para controlar el par electromagnético.
Sin embargo, de la ecuación (5.6) que es la componente en el eje x, de la corriente del
estator orientado al flujo del estator, se encuentra el módulo de la corriente de
→
magnetización del estator ( | i ms | ) y ésta depende del voltaje del estator. Por lo que para
este caso se asumen las siguientes condiciones:
•
La frecuencia de la fuente de alimentación del estator es constante (ωs = cte.) y
•
La resistencia del estator es muy pequeña.
•
El módulo de la corriente de magnetización del estator en estado estacionario
→
(definido en la ecuación (5.4)) es constante (| i ms |= cte.)
•
La velocidad del vector espacial de corriente de magnetización (o de flujo
estatórico) es ω ms = dtd ρ s y también se considera constante. ρ s es el ángulo del
marco de referencia orientado al flujo del estator con respecto al eje sD del marco
de referencia fijo, como se muestra en la siguiente figura explicada en el capítulo 3.
y
rβ sQ
ωs
ir
φr
αr
i ms =
ρs
im
θr
x
rα
sD
Figura 5- 2. Marco de referencia general.
Con estas condiciones la ecuación (5.9) es igual a:
→
→
u sψs = ω ms L m i ms
78
(5. 20)
Capítulo 5
donde:
FOC aplicado al MIDA
→
| u sψs | es el módulo del fasor de voltaje del estator,
ω ms es la velocidad del marco de referencia.
Para el motor de inducción doble alimentado (MIDA), se asume en el estator una fuente
trifásica simétrica senoidal, con frecuencia ωs . Expresando en forma de Euler la fuente
trifásica del estator en un marco de referencia orientado al flujo del estator, el fasor
espacial de voltaje del estator [2], es:
→
→
u sψs = U s e j(ωs t −ρs ) = u sx + ju sy = (u sD + ju sQ )e j(ωs t −ρs ) = u s e j(ωs t −ρs )
(5. 21)
Expresando la misma ecuación en su forma polar:
→
→
u sψs =| u s | ∠(ωs − ρs )
(5. 22)
y en forma de sus componentes x,y en un marco de referencia orientado al flujo del
estator es:
u sx = 0 ,
(5. 23)
→
u sy = u s
La potencia activa del estator en el marco de referencia orientado al flujo del estator se
define como:
 → → 
Ps = 32 ℜ e  u sψs ⋅ i ∗sψs  =


3
2
(u
i + u sy i sy ),
sx sx
(5. 24)
y la potencia reactiva en el marco de referencia orientado al flujo del estator es:
 → → 
Q s = 32 ℑ m  u sψs ⋅ i ∗sψs  =


3
2
(u
i − u sx i sy ) .
sy sx
(5. 25)
Sustituyendo las componentes u sx , u sy de la ecuación (5.23) en las ecuaciones (5.24) y
(5.25), las potencias activa y reactiva se expresan como:
→
Ps =
3
2
u s i sy ,
Qs =
3
2
u s i sx .
79
→
(5. 26)
Capítulo 5
FOC aplicado al MIDA
5.2 Diagrama a bloques de la estrategia de control
Haciendo referencia al esquema de control de la figura 5-1, donde se presenta un
diagrama de señales de Entrada/Salida al sistema de control, se muestra más
detalladamente en la siguiente figura:
ias
ibs
ics
iar
ibr
icr
ω*ref
+-
isD
3a2φ
isQ
irα
3a2φ
irβ
Controlador
Vs
isx
Transformación
orientada al FE isy
∼
Vcs
irx
Transformación
orientada a θr
irβ
iar
ibr
icr
Modelo
bifásico
del MIDA
irα
iry
*
Pref
Q*ref
Vbs
τL
Control
FOC
irx
Transformación
orientada a θr iry
ias
ibs
irc
Vas
2a3φ
τem
θr
ωr
Figura 5- 3. Diagrama esquemático del FOC aplicado al MIDA.
Las variables de entrada al sistema de control FOC son las corrientes del estator y rotor, así
como las potencias activa y reactiva de referencia. La potencia activa de referencia se
obtiene del error de las velocidades mecánicas del rotor, el cuál pasa por un controlador de
velocidad.
La velocidad mecánica de referencia, la potencia reactiva de referencia, el par de carga y
los voltajes del estator son variables de entrada del sistema (variables independientes), y
la velocidad mecánica del rotor, el par electromagnético y las corrientes del estator y rotor
son variables dependientes.
Las variables de corriente del estator y rotor del MIDA se expresan en sus sistemas de
referencia naturales; es decir, las variables del estator están referidas a ejes fijos (ejes
directo y cuadratura, q-d), en tanto que las variables del rotor a ejes que giran a la
velocidad eléctrica ( ω r ) del rotor como se muestra en la figura 5-4.
sQ
sD
ωr
rβ
rα
θr
Figura 5- 4. Sistema de referencia en el marco de referencia natural.
80
Capítulo 5
FOC aplicado al MIDA
A partir del conocimiento de la velocidad mecánica a la que gira el rotor, se estima y
obtiene la velocidad de referencia óptima, mediante el control vectorial de las corrientes
del rotor, según el flujo total estatórico.
En la figura 5-5 se muestra el diagrama a bloques de la estrategia de control, es decir la
implementación del MIDA con un esquema del control orientado al flujo del estator. Se
utiliza como plataforma de simulación MATLAB/Simulink (versión 6.5, 2002).
En la siguiente subsección se explica el esquema general de control orientado al flujo
estatórico aplicado al MIDA (figura 5-5).
5.2.1
Esquema general del control orientado al flujo estatórico aplicado al MIDA
El esquema de control del MIDA se puede dividir en dos lazos de control situados en
cascada (figura 5-5).
a) Lazo interno
Módulo y ángulo
Recordando del capítulo 4, donde se hace mención a la implementación vectorial el cual
requiere de la información del módulo y el ángulo de la corriente de magnetización del
estator. Así el ángulo de la corriente de magnetización, ρ s , se obtiene de las componentes
i msD , i msQ (eje directo y de cuadratura, respectivamente). Dichas componentes pertenecen
a la corriente de magnetización del estator expresada en el marco de referencia fijo (MRF)
y utilizando un convertidor de rectangular a polar (figura 5-5) se obtiene el módulo y el
ángulo de la corriente de magnetización , es decir:
→
i ms ∠ρ = i msD + ji msQ =
Lm
(i sD + i sQ ) + (i rα + ji rβ )e jθr
Ls
(5. 27)
Las corrientes ( i sD , i sQ ) se obtienen de las corrientes trifásicas (i sa , i sb , i sc ) del estator,
aplicando la matriz de transformación de tres a dos fases (ecuación (2.18), del capítulo 2),
en un marco de referencia fijo. De manera análoga, las corrientes ( i rα , i rβ ) se obtienen de
las corrientes trifásicas del rotor
(i ra , i rb , i rc ) ,
aplicando la matriz de transformación
(ecuación (2.18)) de tres a dos fases fijo, para después realizar otra transformación de dos
fases a dos fases con un ángulo θ r . Cabe señalar que está transformación se puede realizar
en sólo paso, es decir transformar las corrientes trifásicas a bifásicas con un ángulo θ r , que
es el ángulo del rotor. La siguiente ecuación muestra las componentes bifásicas (directa y
en cuadratura) de la corriente del rotor en un marco de referencia fijo al rotor
i rd + ji rq = (i rα + ji rβ )e jθr
Así, la ecuación (5.27) también se puede representar como:
→
→
L
i ms = i ms ∠ρ = i msD + ji msQ = m (i sD + i sQ ) + (i rd + ji rq )
Ls
81
(5. 28)
(5. 29)
Capítulo 5
FOC aplicado al MIDA
Corrientes del estator en un marco de referencia orientado al flujo del estator
Las componentes de la corriente del estator son necesarias para obtener las potencias
activa y reactiva medidas, al multiplicarlas con el voltaje del estator.
Las componentes i sx , i sy
de la corriente del estator orientadas al marco de referencia al
flujo del estator, se obtienen de la componentes ( i sD , i sQ ) de la corriente del estator en un
marco de referencia fijo (figura 5-5):
→
(5. 30)
i sψs = i sx + ji sy = (i sD + i sQ )e − jρs
O en forma matricial (ecuación (4.21) del capítulo 4):
i sx   cos ρ s
i  = 
 sy   − sin ρ s
sin ρ s  i sD 
 
cos ρ s  i sQ 
(5. 31)
Corrientes del rotor en un marco de referencia orientado al flujo del estator
Las componentes de la corriente del rotor orientadas en marco de referencia natural
(ecuación (5.28)), se reorientan al marco de referencia orientado al flujo estatórico, como se
muestra en la siguiente ecuación:
i rx + ji ry = (i rd + ji rq )e jρs
(5. 32)
Realizando de esta manera el desacople de las componentes de la corriente del rotor.
b) Lazo externo
En el lazo exterior se realiza el control de velocidad y de la potencia reactiva, llevándolas
a los valores de referencia ω∗rref y Q ∗sref . El control de velocidad da pausa al control de la
potencia activa.
Para poder regular las potencias activa y reactiva, se efectúa el control de la corriente del
rotor en el lazo interno. En dicho lazo interno se realiza el desacople de las componentes
activa, i rx , y reactiva, i ry , de la corriente del rotor, expresadas en los ejes directo y en
cuadratura (x,y) apoyándose en el control orientado al flujo del estator. Así en el marco de
referencia orientado al flujo del estator las componentes i rx , i ry de la corriente del rotor
(directa y en cuadratura, respectivamente), son directamente proporcionales a las
componentes de la corriente del estator (i sx , i sy ). Por lo tanto, la componente irx de la
corriente del estator controla la potencia reactiva (o la componente, i sx , de la corriente del
estator), mientras que la componente iry puede controlar el par electromagnético o, en este
caso a la potencia activa.
82
Capítulo 5
FOC aplicado al MIDA
→
V
3/2
isx
isy
e
isD
− jρ s
3→ 2
isQ
s
isA
isB
isC
Ls/Lm
θr
MIDA
ωr
Ls/Lm
ρs
r
ims
imsD
R→P
+
ird
+
imsQ
+
irq
+
e
jθr
irα
3→ 2
irβ
ira
irb
irc
−
+
Qs
Ps
i rx
e
− jρ s
Voltajes
Desacoplados
i ry
Vdry
Vdrx
PI
Ps ref
K
+
-
−
+
Qs ref
+
-
PI
PI
i ry
iry ref
PI
+
+
i rx
irx ref
PI
+
+
Vˆry
Vˆrx
+
+
+
+
Vra Vrb Vrc
Vry
Vrx
e −j(ρs −θr )
Vrα
Vrβ
2→3
Figura 5- 5. Esquemático del control orientado al flujo estatórico del MIDA.
La diferencia entre los valores medido y de referencia de la potencia activa ( Ps ) del
estator es la entrada al controlador PI y su salida es la componente de referencia i ry
ref
de
la corriente del rotor, expresada en el marco de referencia orientado al flujo del estator. De
forma análoga, el valor de referencia de la potencia reactiva ( Q s ) del estator es comparada
con el valor medido y su diferencia es la entrada a un controlador PI, la salida de esté
controlador es la componente de referencia i rx ref .
La diferencia entre las componentes: medida y de referencia
(i rx , i rxref ) de la corriente del
rotor (eje directo) es la entrada al controlador PI y su salida es el voltaje de referencia en el
83
Capítulo 5
FOC aplicado al MIDA
eje directo del rotor en el marco de referencia orientado al flujo del estator. De manera
análoga se obtiene el voltaje de referencia en el eje de cuadratura (eje y).
Como los voltajes del rotor se encuentran en el marco de referencia orientado al flujo del
estator se reorientan a su marco de referencia natural para luego transformar estos voltajes
bifásicos a trifásicos por medio de la ecuación (2.19) del capítulo 2.
Pasos del algoritmo de Control Orientado según el flujo total del estator, implementado:
1. Transformaciones de 3 a 2 ejes de las corrientes del estator y rotor, en sus
correspondientes ejes naturales.
Se realizan las transformaciones de tres a dos ejes en los ejes directo y cuadratura,
tomando como sistema de referencia que los ejes del estator están fijos y los ejes
del rotor se mueven a velocidad ω r , como se observa en la figura 5-4.
2. Obtención del módulo de la corriente de magnetización i ms del estator y el ángulo
que forma el flujo estatórico, ρ s .
3. Obtención de las componentes isx, isy de la corriente del estator expresada según el
flujo total estatórico.
4. Obtención del fasor de la corriente rotórica (irx, iry) expresada según el flujo total
estatórico ( ρ s ).
5. Obtención de las potencias activa y reactiva (Ps y Qs), a partir del producto del
voltaje estatórico y las componentes de la corriente estatórica.
6. Con la señal de error obtenida de la diferencia de velocidades ( ω rref − ω r ) y la cual
pasa por un control PI que da lugar al par. Dicho par se multiplica por una
ganancia (cte.) para obtener la potencia activa de referencia (Psref).
7. De los errores de las potencias activa y reactiva que pasan a través de unos PI, para
obtener las corrientes de referencia irxref e iryref.
8. De los errores obtenidos de las componentes de la corriente rotórica, se aplican
controladores PI, que dan lugar a las señales de voltaje vrx y vry.
9. Suma de los voltajes de desacoplo con las obtenidas, a fin de mejorar el desacoplo
entre la potencia activa y reactiva.
10. Transformación de los voltajes rotóricos obtenidos a los ejes naturales del rotor.
11. Transformación de 2 a 3 fases de los voltajes.
84
Capítulo 5
FOC aplicado al MIDA
5.3 Resultados de simulación obtenidos al aplicarle el FOC al MIDA
Se considera la misma máquina que se utilizó en el modelado del MIDa en lazo abierto. Y
es una máquina de inducción de 3Hp, trifásica, simétrica, de cuatro polos, con un voltaje de
alimentación de 220V a 60Hz. En el análisis del Motor de Inducción se desprecian los efectos
capacitivos, sólo se modelan los efectos inductivos y resistivos para la parte eléctrica, para
el subsistema mecánico se considera solamente los efectos de la masa de la flecha,
considerando que no existen efectos torsionales y se omiten los efectos de fricción. Dicha
máquina presenta los siguientes valores:
Tabla 5- 1. Parámetros del MIDA
Parámetros
Valor
Potencia del motor (Po)
3 Hp (2237.14 W)
Voltaje del estator de línea a línea en rms (Vm)
220 V
Frecuencia de línea o frecuencia eléctrica
60 Hz
Resistencias del estator (Rs)
0.435 Ω
Resistencias del rotor (Rr)
0.816 Ω
Reactancia de dispersión del devanado del estator (Xls)
0.754 Ω
Reactancia de dispersión del devanado del rotor (Xlr)
0.754 Ω
Reactancia de magnetización (XM)
26.13 Ω
Inercia del rotor (J)
0.089 kg m2
Coeficiente de fricción viscosa (β)
0 (N m s) / (rad)
Deslizamiento
2.8%
Velocidad nominal del rotor
1749.6 rpm=183 rad/seg
Factor de potencia
0.8
Estos son los parámetros que diferentes autores como Krause [11], Ong [12], Chapman[14]
proporcionan para un motor de inducción (tabla 5-1) .
Con los datos de la tabla 5-1 y con el propósito de que la velocidad del motor sea la que se
especifica, se calculo el par de carga nominal (Krause[11], p. 180)
τ L = P0 ⋅
P 1
 4  1 
⋅ = (2237.14 ) 
 = 24.45 Nm
2 ω
 2  183 
85
(5. 33)
Capítulo 5
FOC aplicado al MIDA
Recalcando que para la implementación del control vectorial se requiere de la información
del módulo y el ángulo de la corriente de magnetización del estator. La figura 5-6 muestra
las gráficas del módulo y ángulo (ecuación (5.29)). El ángulo nos sirve para orientar a las
corrientes del estator y rotor en el marco de referencia orientado al flujo del estator.
Figura 5- 6. Módulo de la corriente de magnetización del estator.
La corriente de magnetización muestra un transitorio durante
0.4 segundos
aproximadamente, y tiende a una amplitud constante de 8 Amperes. La amplitud
constante es lógica ya que el fasor de la corriente de magnetización es coaxial al fasor del
flujo del estator (figura 4.14 del capítulo 4).
La figura 5-9, muestra la gráfica del ángulo ρ s , que forma el flujo estatórico con respecto
al eje fijo de estator (vea la figura 4-14). El ángulo ρ s , es constante tiene con una amplitud
pico de 6 rad.
Figura 5- 7. Ángulo ρ s de la corriente de magnetización.
La figura 5-8 muestra las componentes i sx , i sy (directa y en cuadratura) del fasor de la
corriente de estator, orientadas al flujo estatórico. Dichas componentes muestran un
transitorio durante 0.4 segundos aproximadamente y como es de esperarse las
componentes toman valores constantes debido a la orientación.
86
Capítulo 5
FOC aplicado al MIDA
Figura 5- 8. Componentes del fasor de la corriente del estator en un marco de referencia orientado al flujo
del estator.
En la figura 5-9 se muestran las componentes ( i rx , i ry ), del fasor de la corriente de rotor
orientadas al flujo estatórico. Al igual que las componentes del estator muestran un
transitorio durante 0.4 segundos y después de ese tiempo se hacen constantes. La
componente directa toma un valor de 7 amperes aproximadamente, mientras que la
componente en cuadratura se anula.
Figura 5- 9. Componentes del fasor de la corriente del rotor en un marco de referencia orientado al flujo del
estator.
87
Capítulo 5
FOC aplicado al MIDA
La figura 5-10 muestra las componentes de los voltajes en un marco de referencia natural
y muestran un transitorio durante 0.4 segundo para luego establecerse en 3.8 volts. Los
voltajes bifásicos son fuente de alimentación de lado del rotor.
Figura 5- 10. Voltajes del rotor.
Ensayo 1
En el ensayo 1, con un par de carga con un valor de 11.7 N-m, y con una señal de
referencia igual a la velocidad nominal, se observa cómo la señal de la velocidad mecánica
del rotor se mantiene igual a la señal de referencia y cumple con el objetivo principal del
trabajo de tesis que es la regulación de velocidad.
Así, en la figura 5-11 se muestra la velocidad de referencia y la velocidad mecánica del
rotor. La señal punteada es la velocidad de referencia y se encuentra a su valor nominal
(183 rad/seg). La línea es la velocidad mecánica del rotor que se mantiene igual a la señal
de referencia.
88
Capítulo 5
FOC aplicado al MIDA
Figura 5- 11. Velocidad de referencia ( ω ref ) & velocidad mecánica del rotor ( ω mr ).
El sistema no se adelanta a la señal de referencia, tampoco presenta un comportamiento
con sobrepicos y ni oscilaciones. La velocidad mecánica del rotor muestra tener un valor
constante después de 0.4 segundos aproximadamente.
La siguiente figura muestra el par electromagnético del MIDA, el par tiene un valor de
11.8 N-m en estado estacionario. Este valor es igual al valor del par de carga.
Figura 5- 12. Par electromagnético en N-m
Ensayo 2
En el ensayo 2, se considera un par de carga igual a 24.5 N-m y se obtiene nuevamente la
gráfica de velocidades (referencia y medida), así como la gráfica del par electromagnético.
Esto con la finalidad de observar que la velocidad mecánica del rotor se sostiene cerca de
la velocidad nominal.
89
Capítulo 5
FOC aplicado al MIDA
La siguiente figura muestra la gráfica de velocidades. La velocidad de referencia es la
señal punteada mientras que la señal de la velocidad mecánica del rotor es la línea.
Figura 5- 13. Velocidad de referencia ( ω ref ) & velocidad mecánica del rotor ( ω mr ).
Para un par de carga nominal, la velocidad mecánica del rotor presenta un error de 1.59%,
el cuál esta dentro del limite aceptado.
La figura 5-14 muestra la gráfica del par electromagnético y muestra una etapa transitoria
con oscilaciones que termina después 04 segundos. Después de esta etapa el par
electromagnético tiende a un valor constante que es igual al par de carga, en este caso es
igual 24.5 N-m.
Figura 5- 14. Par electromagnético en N-m
90
Capítulo 5
FOC aplicado al MIDA
Conclusiones
En este trabajo se utiliza el control orientado al flujo del estator, debido a que se requieren las
corrientes sinusoidales del estator y el desacoplamiento de las potencias activa y reactiva.
Este tipo de control asegura el desacoplamiento requerido para el control apropiado de la
amplitud y ángulo de fase del fasor espacial de la corriente del rotor. Además tiene la
ventaja de estabilizar al motor.
Estas características las ofrecen también los otros controles pero en base a la revisión
bibliográfica la mayoría de los autores recomiendan este control específicamente cuando
se trata de máquinas doble alimentadas.
El esquema de control para el MIDA es un esquema adaptado del propuesto por Vas [2],
el cual controla las potencias activa y reactiva. Y se adapto para el control de regulación de
velocidad.
La estrategia de control plateada en este capitulo para el control de velocidad resulto
aceptable debido a que para un par de carga diferente a cero la señal de velocidad sigue a
la señal de referencia con un margen de error es del 2 %.
El par de carga se recomienda que no sea mayor al par de carga nominal porque la
máquina entraría a la región de inestabilidad.
La principal aportación de este trabajo es el desarrollo de un esquema que además de
controlar las potencias activa y reactiva controle la velocidad de un motor de inducción
doble alimentado.
91
CONCLUSIONES
“CONTROL VECTORIAL DE UNA MÁQUINA DE INDUCCIÓN DOBLE
ALIMENTADA”
Este trabajo está orientado al control de motores de corriente alterna (ca), específicamente
a un motor asincrónico o de inducción, de tipo “rotor devanado”. Estos motores son más
robustos y económicos que los motores equivalentes de cd [17], debido fundamentalmente
a que no se necesita una fuente de corriente externa al rotor para crear un campo
magnético en éste.
La máquina de inducción doble alimentada (MIDA), se caracteriza porque tiene su estator
conectado a una fuente de alimentación de frecuencia constante y su rotor conectado a un
convertidor estático bidireccional. Así la MIDA puede estar alimentada y controlada desde
el estator o desde el rotor o desde ambos. De las diferentes combinaciones posibles, el
control del lado del rotor es la parte ventajosa ya que el convertidor de potencia sólo
necesita manipular la potencia de deslizamiento.
El alcance del trabajo de tesis fue el desarrollo de un esquema de control de velocidad para
un motor de inducción de doble alimentado (MIDA), mediante la aplicación del control
vectorial. La aplicación del control vectorial (FOC) al MIDA se realizó en el capítulo 4 y se
explican los resultados obtenidos más adelante.
Las metas alcanzadas fueron:
•
El análisis del flujo de potencias del MIDA.
El control para una máquina de inducción doble alimentada se coloca del lado del rotor
por que fue indispensable realizar el análisis del flujo de potencias mediante diagramas de
los flujos de las potencias y siguiendo la convención de signos se estableció la dirección de
las potencias.
Como el objetivo de la tesis fue trabajar en modo motor, en ambos casos (velocidad sub y
super-síncrona) la potencia del estator ( Ps ), es entrante. La potencia mecánica Pm , siempre
será saliente y la potencia del rotor Pr , solo será saliente a velocidades sub-síncronas y
entrante a velocidades super-síncronas. Estos signos de las potencias se tomó como base
en el desarrollo de la tesis.
93
Conclusiones
Con este análisis se aseguró el modo de operación
velocidades sub-síncronas y super-síncronas.
•
(modo motor) de la máquina a
El modelo matemático y análisis en estado estacionario del motor de inducción de
rotor devanado en configuración doble alimentado.
La máquina de inducción doble alimentada en modo motor puede operar a velocidades
sub-síncronas (por debajo de la velocidad de síncronismo) y super-síncronas (por encima
de la velocidad de síncronismo).
En el análisis del MIDA en estado estacionario, se calcularon los valores de las corrientes
del estator y rotor para determinar los parámetros de rendimiento del MIDA, con la
finalidad de calcular la potencia mecánica total y el par electromagnético a velocidades
sub-síncronas y super-síncronas.
Lo relevante del análisis del MIDA en estado estacionario fue la obtención de tres pares
electromagnéticos y son:
1) El par asíncrono constante τ s para un deslizamiento dado, producido por el voltaje
suministrado al estator. Esté par actúa como par-motor en operación sub-síncrona
es decir en el intervalo de 0 < s < 1 y como par-regenerados en operación supersíncrona ( − 1 < s < 0 ).
2) Par asíncrono constante τ r para un deslizamiento dado, producido por el voltaje
aplicado al rotor. El par actúa como par-regenerador en ambas operaciones subsíncrona y super-síncrona.
3) Par producido por la interacción de los campos del estator y rotor ( τ sr ). El par es
producido por la interacción de ambos campos y se observó que en operación subsíncrona se tiene un par regenerador y en modo super-síncrono un par motor.
4) Par total es la suma de los tres pares descritos anteriormente y en operación subsíncrona produce un par-motor y un par-regenerador en operación super-síncrona.
El MIDA presenta estos tres pares debido a la doble alimentación (desde el estator y del
lado del rotor). Y del par total se obtuvo información del comportamiento de la máquina
de inducción en configuración doble alimentada. Además, con el par electromagnético
total se comprobó el modo de operación.
Una forma de saber en qué modo de operación esta la máquina es a través del signo del
par electromagnético, si es positivo la máquina esta en modo motor y en caso contrario
(negativo) se estará trabajando en modo generador.
94
Conclusiones
Del par total obtenido se concluyó que es un par electromagnético positivo porque al
graficar el par total muestra una curva en el cuadrante positivo (lado sub-síncrono). Así el
MIDA se encuentra en modo motor, que es el modo de operación planteado para el
desarrollo del trabajo de tesis.
•
La simulación digital del MIDA en lazo abierto, utilizando la herramienta
“Simulink” de Matlab.
La teoría de Marcos de Referencia tiene varias aplicaciones en el campo de ingeniería
eléctrica como son el análisis de maquinaria eléctrica, el análisis de sistemas eléctricos de
potencia y el análisis de sistemas impulsores de velocidad variable; sin embargo, en éste
trabajo se aplica al MIDA.
Las ecuaciones del motor de inducción trifásico, muestran un sistema no lineal, variante en
el tiempo y acoplado. El acoplamiento se presenta por que la derivada de cualquiera de las
variables depende de otras variables y algunas de las inductancias de la máquina están en
función de la posición angular del rotor, por lo que los coeficientes de las ecuaciones
diferenciales son variantes en el tiempo.
El sistema trifásico del motor de inducción tiene ocho variables de estado dando como
resultado un sistema de orden 8. Seis ecuaciones en el subsistema eléctrico y dos en el
subsistema mecánico. Con la finalidad de reducir la complejidad de estas ecuaciones
diferenciales, se empleó un modelo matemático equivalente bifásico (Teoría de Marcos de
Referencia). Este modelo matemático equivalente reduce el orden del sistema de ocho a
seis. Además, permitió que fuera más fácil el diseño del control, y facilitó la
programación de simulación del sistema.
En este trabajo de tesis se eligió el marco de referencia fijo al estator, debido a la
conveniencia en la interpretación de las graficas de simulación. Es decir, como se trabajo
en un marco de referencia fijo al estator, la frecuencia de las corrientes bifásicas (estator y
rotor) y voltajes bifásicos, es igual a la frecuencia base o frecuencia de la fuente de
alimentación.
La transformación matemática de tres a dos fases más utilizada, es conocida como
transformación de Park [12].
En está primera fase la simulación del modelado del MIDA se realiza en lazo abierto en
un marco de referencia fijo al estator. Se utilizó como plataforma de simulación
MATLAB/Simulink (versión 6.5, 202).
Una forma de comprobar que el sistema funcionara bien fue cortocircuitar al rotor es decir
poner los voltajes bifásicos del rotor igual a cero, obteniendo de esta manera el modelo de
un motor jaula de ardilla y se comprobaron los resultados de las graficas de las corrientes
del estator y rotor, la velocidad, par electromagnético con las presentadas en Krause [11],
Ong [12] y Novotny [18].
95
Conclusiones
•
Diseño de un sistema de control de la velocidad de un MIDA basado en el control
vectorial.
Existen varias técnicas para controlar a el MIDA, en este trabajo se utilizo la técnica del
control vectorial por la ventaja que presenta en el desacoplamiento de las variables del
motor, permitiendo obtener un comportamiento dinámico similar al de un motor de cd.
El control vectorial se basa en rescribir las ecuaciones dinámicas de la máquina de
inducción en un marco de referencia que se orienta según flujo y puede ser orientado: al
flujo estatórico, al flujo rotórico o al de magnetización de tal manera que en el nuevo
marco de referencia aparece una relación lineal entre la variable de control y la velocidad.
En todos los marcos de referencia, la transformación de coordenadas se realiza ubicando el
eje x del marco de referencia, coaxial con el fasor de flujo del rotor, estator o de
magnetización, de tal forma que la expresión del par electromagnético resulta del
producto de dos corrientes en cuadratura; Así, la expresión que modela a la máquina de
inducción resulta ser un control de las corrientes en forma independiente como las
expresiones de una máquina de cd con excitación independiente.
En el control de una máquina de inducción se deben conocer dos parámetros y son: el par
y el flujo en el entrehierro. El par es necesario cuando se detecta un error en la velocidad
mecánica deseada y el flujo en el entrehierro es necesario para evitar que la máquina entre
en la zona de saturación.
En este trabajo se utiliza el control orientado al flujo del estator, debido a que se requieren las
corrientes sinusoidales del estator y el desacoplamiento de las potencias activa y reactiva.
Este tipo de control asegura el desacoplamiento requerido para el control apropiado de la
amplitud y ángulo de fase del fasor espacial de la corriente del rotor. Además tiene la
ventaja de estabilizar al motor.
Los otros dos métodos de control orientados al flujo rotórico y de magnetización también
proporcionan estas características pero la elección se baso en la revisión bibliografía, ya
que la mayoría de los autores [2] [19] sugieren la aplicación del control orientado al flujo del
estator al MIDA.
El esquema de control orientado al flujo estatórico se presento en el capítulo 4 y es un
esquema adaptado del esquema propuesto por Vas [2] que solo controla las potencias
activa y reactiva. La adaptación se hizo para el control de velocidad del MIDA
En este trabajo de tesis el modelo del convertidor es ideal, ya que se supuso que se generan
las ondas de voltaje del rotor senoidales, que son iguales a las ondas de referencia
correspondientes a las generadas por el controlador.
Existen dos métodos de adquisición del módulo y ángulo, que son: directo e indirecto. En
el desarrollo del trabajo de tesis se utilizo el método indirecto ya que el módulo y el ángulo
96
Conclusiones
del fasor de flujo estatórico, se obtienen a partir de las ecuaciones de las corriente del
estator y rotor, y de la velocidad del rotor. A diferencia del control directo, el módulo y
ángulo del fasor de flujo se miden directamente con sensores.
•
Simulación del control de velocidad del motor de inducción doble alimentado,
utilizando la herramienta de MATLAB/ Simulink.
Para el modelado de la máquina de inducción trifásica se debe tomar en cuenta que en
condiciones normales de operación, los circuitos eléctricos son balanceados y simétricos.
Las gráficas de las componentes del fasor de corriente estatórica y rotórica muestran sus
componentes constantes una tiene una amplitud positiva y la otra se anula o su amplitud
es negativa y esto es valido por la orientación de las variables al flujo estatórico.
Para un par igual a 9 N-m la velocidad de referencia siguió a la velocidad nominal sin
ningún porcentaje de error.
La estrategia de control plateada para el control de velocidad resulta aceptable debido a
que para un par de carga nominal la señal de velocidad siguió a la señal de referencia con
un margen de error es del 2 %.
La principal aportación de este trabajo es el desarrollo de un esquema de control de
velocidad para un motor de inducción doble alimentado.
TRABAJOS FUTUROS
•
Control de velocidad para el MIDA utilizando un convertidor de flujo de potencia
bidireccional.
•
Control de velocidad para el MIDA sin omitir los efectos capacitivos en el
subsistema eléctrico y considerando los efectos torsionales y de fricción.
•
Al análisis del MIDA con sistemas de alimentación no balanceados.
97
REFERENCIAS
[1]
Irving L. Kosow, Máquinas Eléctricas y Transformadores, Ed. Reverté, 1992.
[2]
Peter Vas, Vector Control of AC Machines, Clarendon Press-Oxford, 1990.
[3]
Texas Instruments, Digital Signal Processing Solution for AC Induction Motor,
Application Note BPRA043, 1996.
[4]
S. Alepuz, V. Delos, J. Ma. Horrillo, “Control Vectorial de Motores de
Inducción”, Mundo Electrónico, junio 2000, pp.44-51.
[5]
Zhenyu. Yu., Figoli. David, AC Induction Motor Control Using Constant V/Hz
Principle and Space Vector PWM Technique with TMS320C240, Application
Report: SPRA284A, Texas Instruments, April 1998.
[6]
Gerardo V. Guerrero Ramírez, Modelado y Simulación de un Sistemas Impulsor
de Motores de Inducción Trifásicos, CENIDET, 1994.
[7]
Miguel Ángel Méndez Bolio, Controladores de Motores de Inducción: Un
Análisis Comparativo, Tesis de Maestría, Cenidet, Cuernavaca Morelos,
marzo 2001.
[8]
Paresh C. Sen, Principles of Electric Machines and Power Electronics, Ed Wiley,
1989.
[9]
Theodore Wildi, Electrical Machines, Drives and Power Systems”, Fourth
edition, Prentice Hall.
[10] Debiprasad Panda, Eric L. Benedict, “A Novel Control Strategy for the
Rotor Side Control of a Doubly-Fed Induction Machine”, IEEE.
[11] Paul C. Krause,
Company, 1987 .
Analysis of Electric Machinery, McGraw-Hill Book
[12] Chee-Mung Ong, Dynamic Simulation of Electric Machinery,
MATLAB/simulink, 1a. Edición, Indiana, Prentice Hall PTR, 1998.
using
[13] F. Blaschke, "The Principle of Field Orientation as Applied to the New
TRANSVEKTOR Closed-Lood
Control System for Rotating-Field
Machines", Siemens Review, Vol.34, mayo 1972.
[14] Stephen J. Chapman, Máquinas Eléctricas, Ed McGraw-Hill, 1993.
[15] R. Gabriel, W. Leonhard & C. Nordby, "Field Oriented Control of Standard
AC, Motor Using
Microprocessors", IEEE Transactions on Industry
Applications, Vol. IA 16,Mar/ Apr. 1980,pp. 186-192
[16] Texas Instruments, Field Orientated Control of 3-Phase AC- Motors, Literature
Number: BPRA073, February 1998.
[17] Muhammad H. Rashid, ELECTRONICA DE POTENCIA circuitos,
dispositivos y aplicaciones, Ed. McGraw-Hill.
99
[18] D. W. Novotny and T. A. Lipo, Vector Control and Dynamics of AC Drives,
Clarendon Press- Oxford, 1996.
[19] Andrzej M. Trzynaldowski, Control of Induction Motors”, Academic Press,
2001.
[20] A. Mebarki and R. T. Lipczynski, "A novel variable speed constant
frequency generation system with voltage regulation", Sevilla Enero ’95,
University of Bath. UK.
Direcciones de internet: www.ti.com, www.ieee.com.
100
BIBLIOGRAFÍA ADICIONAL
[1]
Denis O’Kekky, Performance and Control of Electrical Machines, Ed. McGraw –
Hill, 1992.
[2]
Andrzej M. Trzynaldowski, Control of Induction Motors, Academic Press,
2001.
[3]
Clarence A. Phipps, Variable Speed Drive Fundamentals, The Fairmont
Press, Inc.3a Ed., 1999.
[4]
B. K. Bose, Power Electronics and Drives, Ed. Prentice Hall, 1986.
[5]
Werner Leonhard, Control of Electrical Drives, Springer Verlag, 1986.
[6]
Peater Vas, Electrical Machines and Drives, Oxford, 1992.
[7]
Ion Boldea, Vector Control of AC Drives, CRC Press, Inc., 2000.
[8]
Denis O’Kelly, Performance and Control of electrical Machines, McGraw-Hill
Book Company, 1992.
[9]
YIFAN TANG, LONGYA XU. “Vector Control and Fuzzy Logic Control of
Doubly Fed Variable Speed Drivers with DSP Implementation”, IEEE Transactions
on Energy Conversion, Vol.10, No. 4, December, 1995, pp. 661-668.
[10]
MS. ING. RODOLFO MORENO MARTÍNEZ, “Control Vectorial de 4 Cuadrantes
para Motor de Inducción con Rectificador Autoconmutado para la mejora del
Factor de Potencia”, Universidad Nacional de Ingeniería, Facultad de Ingeniería
Eléctrica y Electrónica.
[11]
B. V. GORTI, G.C. ALEXANDER, R. SPÉE “Power Balance Considerations for
Brushless Doubly-Fed Machines”, IEEE Transactions on Energy Conversion, Vol.
11, No. 4, December, 1996, pp. 687-692
[12]
RAJIB DATTA, [and] V. T. RANGANATHAN “Direct Power Control of GridConnected Wound Rotor Induction Machine Without Rotor Position Sensors”,
IEEE Transactions on Power Electronics, Vol. 16, No. 3, May, 2001, pp. 390-786.
[13]
RAJIB DATTA, [and] V. T. RANGANATHAN “A simple Position-Sensorless
Algorith for Rotor-Side Field-Oriented Control of Wound-Rotor Induction
Machine”, IEEE Transactions on Industrial Electronics, Vol. 48, No. 4, August,
2001, pp. 786-793.
[14]
G. DIANA, R.G. HARLEY “An aid for Teaching Field Oriented Control Applied
to Induction Machines”, IEEE Transactions on Power Systems, Vol. 4, No. 3,
August, 1989, pp. 1258-1262
101
Anexo
ANEXO 1
Programa de variables en Matlab del MIDA en lazo abierto
% Parámetros de un Motor de Inducción de 3hp, a 60Hz, 3 fases, 4 polos.
% Voltaje de alimentación (línea) =220v
%Programa en simulink: LAMIDA.mdl
clear all
% Parámetros de un MI trifásico de 3 hp
Pn = 3/(1.341e-3); %Potencia de salida (Po) en Watts (Potencia nominal)
fp = 0.8;
%Factor de potencia
VL = 220;
%Voltaje de línea a línea (V)
P = 4;
%numero de polos
NPp=P/2;
%numero de pares de polos
s= 0.028
%deslizamiento del 2.8%
fb = 60;
%frecuencia nominal (Hz)
fe= fb;
%frecuencia del sistema
wb = 2*pi*fb;
%frecuencia eléctrica base(rad/seg)
fr =s*fe;
%frecuencia del rotor
wr=2*pi*fr;
%frecuencia eléctrica del rotor(rad/seg)
wbm = 2*wb/P;
%frecuencia mecánica base
%Voltajes de Fase del Estator y Rotor
Vm =VL*sqrt(2/3); %Magnitud del voltaje de fase del estator
Vmr=22*sqrt(2/3); %Magnitud del voltaje de fase del rotor
cTem=(3/2)*NPp; %Constante del Par Electromagnético
% Valores del MI
rs =.435;
%resistencia del estator(ohms)
rr =.816;
%resistencia del rotor(ohms)
%Lo datos dados por Krause son admitancias, se divide por la frec. base
Lls=0.754/wb; %Inductancia de dispersión del estator
Llr=Lls;
%Inductancia de dispersión del rotor
Lm =26.13/wb; %Inductancia de magnetización del estator
J = 0.089;
%Inercia del rotor en kg m2
cFv = 0;
%Coeficiente de fricción viscosa
%
% Matriz de enlaces de flujo
L = [Lls+Lm 0 Lm
0;
0 Lls+Lm 0 Lm;
Lm
0 Llr+Lm 0;
0 Lm
0 Llr+Lm];
IL = inv(L);
%Para un deslizamiento nominal del 2.8%
Nnom = 1749.6;
%velocidad mecánica del rotor nominal (rev/min)
WmrN=2*pi*Nnom/60 %velocidad mecánica del rotor en rad/seg
Trated =(Sb/WmrN)
% Par nominal
%Condicciones Iniciales
Psiqso =0; %Eje q del estator
103
Anexo
Psipqro=0; %Eje q del rotor.
Psidso =0; %Eje d del estator.
Psipdro=0; %Eje d del rotor.
wrbywbo=0; %velocidad del rotor
tstop =1.5; %Tiempo de simulación 2 seg
%................................
Programa de variables en Matlab del FOC aplicado al MIDA
%% Parámetros de un MI de 3hp, a 60Hz,
%% 3 fases, 4 polos. Voltaje de alimentación
%% (línea) =220v . Programa en simulink: COMIDA.mdl
clear all % clear workspace
fp=.81;
%factor de potencia
Po=3/(1.341e-3); %Potencia de salida en Watts o Pot.Act.
Sa=Po/cos(fp); %Potencia aparente
Qref=Sa*sin(fp); %Potencia Reactiva de referencia
%----------------------------------------------V1 = 220;
%Voltaje de línea a línea (V)
NPp=4/2;
%Numero de pares de polos
s= 0.028
%deslizamiento del 2.8%
fb= 60;
%frecuencia nominal (Hz)
wb= 2*pi*fb;
%frecuencia eléctrica base(rad/seg)
wbm = 2*wb/P; %frecuencia mecanica base
%Voltajes de Fase del Estator
Vm =V1*sqrt(2/3); %Magnitud del voltaje de fase
cTem=(3/2)*NPp; % Constante del Par Electromagnético
%Valores del MI
rs =.435;
%resistencia del estator (ohms)
rr =.816;
%resistencia del rotor (ohms)
Lls=0.754/wb; %Inductancia de dispersión del estator
Llr=Lls;
%Inductancia de dispersión del rotor
Lm =26.13/wb; %Inductancia de magnetización del estator
J = 0.089;
%Inercia del rotor en kg m2
Ls = Lm + Lls; %Autoinductancia del estator
Lr = Lm + Llr; % Autoinductancia del rotor
Lrp=Lr-((Lm*Lm)/Ls); % Lr prima
cFv = 0;
%Coeficiente de fricción viscosa
cTem=(3/2)*NPp; %Constante del Par Electromagnético
%
% Matriz de enlaces de flujo
L = [Lls+Lm 0 Lm
0;
0 Lls+Lm 0 Lm;
Lm
0 Llr+Lm 0;
0 Lm
0 Llr+Lm];
IL = inv(L);
%----------------------------------------
104
Anexo
%Condiciones Iniciales
Psiqso =0;
%Eje q del estator, Enlaces de flujo total
Psipqro=0; %Eje q del rotor, Enl. de flujo total
Psidso =0;
%Eje d del estator, Enl. de flujo total
Psipdro=0; %Eje d del rotor, Enl. de flujo total
wrbywbo=0; %velocidad del rotor
tstop =2;%Tiempo de simulación 2 seg
%................................
time_wref=[0 0.3 tstop];
% speed_wref=[0 wbm wbm];
speed_wref=[0 183 183];
%................................
% Transfiere el teclado
disp('Ejecuta la simulación, teclea return para graficar');
keyboard
clf;
105
Anexo
ANEXO 2
Los bloques que se presentan a continuación se explicaron en los capítulos 3 y 5.
DIAGRAMA EN SIMULINK DEL MIDA EN LAZO ABIERTO
A. 1. Bloque principal del MIDA en lazo abierto
106
Anexo
V m *co s(u [1 ])
Vas
Van
V m r*(co s(u [1 ]+(p i /8 )))
V o l ta j e fa se a d e e sta to r
V o l ta j e fa se a d e ro to r
1
1
V m *co s(u [1 ]-2 *p i /3 )
In _ w*t
Var
Var
Vbs
Vbn
V m r*(co s(u [1 ]-(2 *p i /3 )+(p i /8 )))
i n _ w_ ro to r
Vc s
V m r*(co s(u [1 ]+(2 *p i /3 )+(p i /8 )))
V cn
Vc r
vo l ta j e fa se c d e ro to r
vo l ta j e fa se c d e e sta to r
A. 2. Interior del bloque Voltajes del estator
A. 3. Interior del bloque Voltajes del rotor
S IM UL A CIÓ N
M o to r d e In d u cci ó n DA e n u n M a rco d e Re fe re n ci a Fi j o a l E sta to r
V o l ta j e s d e l E sta to r
3 a 2
[V an]
vq s
[V bn ]
vd s
[V cn]
V o l ta j e s d e l e sta to r
3 a 2
V o l ta j e s d e l Ro to r
3 a 2
[V ar]
vq r
[V br]
vd r
[V cr]
V o l ta j e s d e l ro to r
3 a 2
in_T L
|
.
S u b si ste m a E l é ctri co
|
.
|
.
Lqs
|
.
Lds
|
Lqr
.
|
Ldr
.
|
E cs. Di fs.
.
Co rri e n te s y E n l a ce s d e F
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
S u n si ste m a M e cá n i co
7
o u t_ T e m
8
o u t_ wm r
9
o u t_ T h e ta _ r
T e m , V e l m e c, P o si ci ó n
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
Co rri e n te s tri fá si ca s
E sta to r y Ro to r
1
o u t_ i sa
2
o u t_ i sb
3
o u t_ i sc
q d s2 a b c
4
o u t_ i ra
ibr
ic r
[t]
[t]
vq d
[vq s]
M ux
V o l ta j e s(q d )
[i q s]
M ux
cq d s
Co rri e n te s(q d )
[i d s]
[vd s]
[t]
[t]
[vq r]
M ux
V o l ta j e s q d
e sta to r y ro to r
vq d r
[vd r]
[i q r]
[i d r]
M ux
Co rri e n te s q d
e sta to r y ro to r
cq d r
Co rri e n te s(q d )1
V o l ta j e s(q d )1
A. 4. Interior del bloque MI en un MRF
107
6
o u t_ i rc
q d r2 a b cr
............................................................................G RA FICA S ...................................................................................
Co rri e n te s b i fa si ca s d e l
E sta to r y Ro to r
5
o u t_ i rb
1
V o l ta j e s b i fa si co s d e l
E sta to r y Ro to r
Vbr
vo l ta j e fa se b d e ro to r
vo l ta j e fa se b d e e sta to r
V m *co s(u [1 ]+2 *p i /3 )
Vbr
V cr
Anexo
1
1
(2*u[1] - u[2]-u[3])/3
In_Vsa
2
abc2qds_F1
Mux
In_Vra
out_Vqs
2
(2*u[1] - u[2]-u[3])/3
Mux
In_Vrb
In_Vsb
(u[3]-u[2])/sqrt(3)
2
3
abc2qds_F2
out_Vds
In_Vrc
3
In_Vsc
1
1
out_Vqr
abc2qds_F1
(u[3]-u[2])/sqrt(3)
2
abc2qds_F2
out_Vdr
Mux
Mux
A. 5. Interior del bloque Voltajes del estator de 3 a 2. A. 6. Interior del bloque Voltajes del rotor de 3 a 2
En los bloques A.5 y A.6 se transforman los voltajes trifásicos a bifásicos de estator y rotor
respectivamente.
Variables del Estator
[iqs]
Mux
[vqs]
Mux
u[2] - rs*u[1]
1
s
1.5
PSIqs
u[2] - rs*u[1]
1
s
1.2
PSIds
[ids]
Mux
[vds]
Mux2
1
Lqs
out_Lqs
Lds
2
out_Lds
iqs
Variables del Rotor
ids
[iqr]
IL* u
[Ldr]
Mux
[wrb]
[vqr]
u[4] + NPp*u[2]*u(3) - rr*u[1]
1
s
1.3
PSIqr
u[4] - NPp*u[2]*u(3) - rr*u[1]
1
s
1.4
PSIdr
Lqr
3
out_Lqr
em
Matrix
Gain
Mux1
[idr]
[Lqr]
Mux
[wrb]
Lqr
4
out_Lqr1
[vdr]
Mux3
A. 7. Interior del bloque corrientes y enlaces de flujo
Aquí se obtienen las corrientes y en laces de flujo bifásicos del estator y rotor.
108
iqr
idr
Anexo
A. 8. Interior del bloque Tem, Vel. Mecánica, Posición
En el bloque A.8 se obtiene el par electromagnético, la velocidad mecánica del rotor y la
posición.
u [1 ]
1
ias
Fcn
[i q s]
M ux
-(u [1 ]+sq rt(3 )*u [2 ])/2
2
Fcn 1
ibs
-(u [1 ]-sq rt(3 )*u [2 ])/2
3
Fcn 2
i cs
[i d s]
M ux
A. 9. Interior del bloque Corrientes qds2abc.
El bloque A.9 contiene a las corrientes bifásicas del estator y las transforma a corrientes
trifásicas
[i q r]
u [1 ]*co s(u [3 ]) -u [2 ]*si n (u [3 ])
[i d r]
M ux
M ux
i q s^s
M ux
i d s^s
1
Fcn
o u t_ i a r
-(u [1 ]+sq rt(3 )*u [2 ])/2
2
Fcn 1
o u t_ i b r
-(u [1 ]-sq rt(3 )*u [2 ])/2
3
Fcn 2
o u t_ i cr
u [1 ]*si n (u [3 ]) + u [2 ]*co s(u [3 ])
1
u [1 ]
th e ta _ r
M u x1
A. 10. Interior del bloque qdr2abcr
Aquí las corrientes bifásicas del rotor se transforman a corrientes trifásicas
109
Anexo
DIAGRAMA EN SIMULINK DEL FOC APLICADO AL MIDA
A. 11. Control vectorial aplicado al MIDA
110
Anexo
A. 12. Interior del bloque Rec a polar
Este bloque se encarga de transformar las componentes de la corriente de magnetización a
su forma polar para obtener el módulo de la corriente de magnetización y el ángulo ρ s
A. 13. Interior del bloque e^j(Rho_s)
En el bloque A.13 las corrientes del estator se ponen en el marco de referencia orientado al
flujo del estator
A. 14. Interior del bloque P=Vi(sx,sy)
En el bloque A.14 se obtienen las potencias activa y reactiva
111
Anexo
A. 15. Interior del bloque voltajes desacoplados
El bloque A.14 se utiliza con la finalidad de mejorar el desacople de las potencias activa y
reactiva
A. 16. Interior del bloque e^-j(Rho_s – Theta_r)
Los voltajes del rotor orientados al marco de referencia del flujo del estator se reorientan a
su marco de referencia natural.
112