Problemas para el Cuarto Parcial - curso promoción directa de la
Anuncio
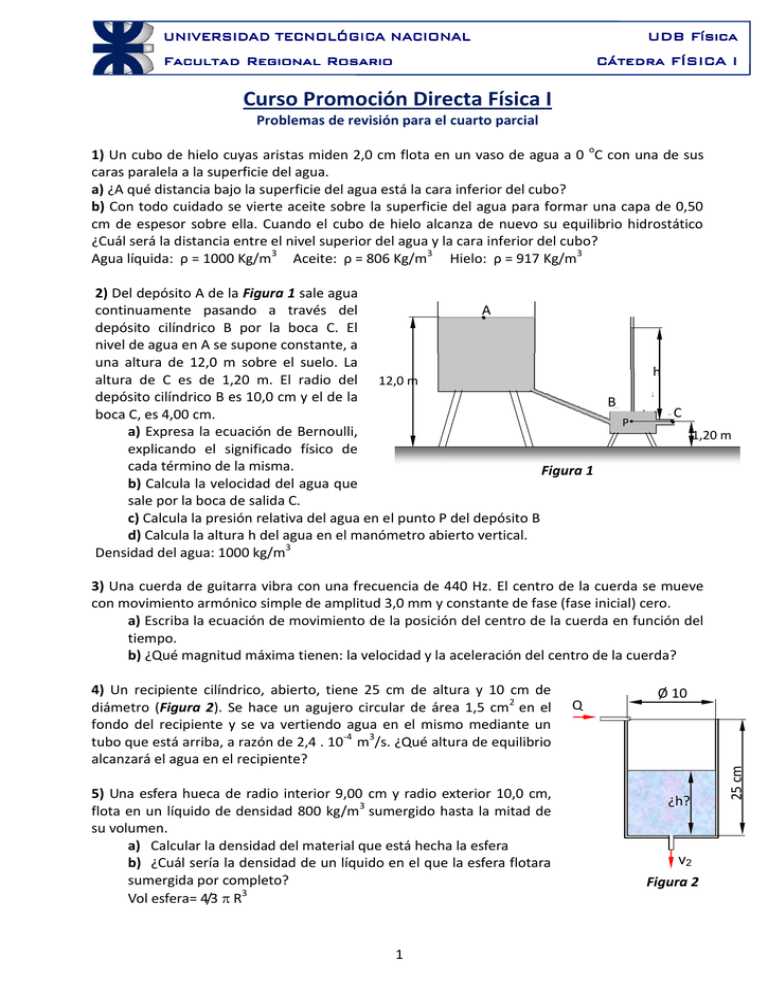
UDB Física UNIVERSIDAD TECNOLÓGICA NACIONAL Cátedra FÍSICA I Facultad Regional Rosario Curso Promoción Directa Física I Problemas de revisión para el cuarto parcial 1) Un cubo de hielo cuyas aristas miden 2,0 cm flota en un vaso de agua a 0 oC con una de sus caras paralela a la superficie del agua. a) ¿A qué distancia bajo la superficie del agua está la cara inferior del cubo? b) Con todo cuidado se vierte aceite sobre la superficie del agua para formar una capa de 0,50 cm de espesor sobre ella. Cuando el cubo de hielo alcanza de nuevo su equilibrio hidrostático ¿Cuál será la distancia entre el nivel superior del agua y la cara inferior del cubo? Agua líquida: ρ = 1000 Kg/m3 Aceite: ρ = 806 Kg/m3 Hielo: ρ = 917 Kg/m3 2) Del depósito A de la Figura 1 sale agua A continuamente pasando a través del depósito cilíndrico B por la boca C. El nivel de agua en A se supone constante, a una altura de 12,0 m sobre el suelo. La A altura de C es de 1,20 m. El radio del 12,0 m depósito cilíndrico B es 10,0 cm y el de la B boca C, es 4,00 cm. P a) Expresa la ecuación de Bernoulli, explicando el significado físico de cada término de la misma. Figura 1 b) Calcula la velocidad del agua que sale por la boca de salida C. c) Calcula la presión relativa del agua en el punto P del depósito B d) Calcula la altura h del agua en el manómetro abierto vertical. Densidad del agua: 1000 kg/m3 h C 1,20 m 3) Una cuerda de guitarra vibra con una frecuencia de 440 Hz. El centro de la cuerda se mueve con movimiento armónico simple de amplitud 3,0 mm y constante de fase (fase inicial) cero. a) Escriba la ecuación de movimiento de la posición del centro de la cuerda en función del tiempo. b) ¿Qué magnitud máxima tienen: la velocidad y la aceleración del centro de la cuerda? 5) Una esfera hueca de radio interior 9,00 cm y radio exterior 10,0 cm, flota en un líquido de densidad 800 kg/m3 sumergido hasta la mitad de su volumen. a) Calcular la densidad del material que está hecha la esfera b) ¿Cuál sería la densidad de un líquido en el que la esfera flotara sumergida por completo? Vol esfera= 4/3 R3 1 Q Ø 10 ¿h? v2 Figura 2 25 cm 4) Un recipiente cilíndrico, abierto, tiene 25 cm de altura y 10 cm de diámetro (Figura 2). Se hace un agujero circular de área 1,5 cm2 en el fondo del recipiente y se va vertiendo agua en el mismo mediante un tubo que está arriba, a razón de 2,4 . 10-4 m3/s. ¿Qué altura de equilibrio alcanzará el agua en el recipiente? 6) Un cuerpo de 200 gramos unido a un resorte de constante elástica K = 20 N/m oscila con una amplitud de 5,0 cm sobre una superficie horizontal sin rozamiento. a) Calcular la energía total del sistema y la velocidad máxima del cuerpo. b) Hallar la velocidad del cuerpo cuando se encuentra a 3,0 cm de la posición de equilibrio. c) Hallar la energía cinética y potencial elástica del sistema en esa posición. d) ¿Para qué posiciones la velocidad del sistema es igual a 0,20 m/s? 7) El cubo A de la Figura 3 a) de 10,0 cm arista y densidad A flota en un líquido de densidad 1000 kg/m3, de modo que está sumergido el 80,0 % de su volumen. Otro cubo de igual densidad que A se apoya sobre éste y se observa en la Figura 3 b) que se sumerge al ras del líquido, es decir su cara superior queda en la superficie de separación aire líquido. a) Calcula la densidad de los cubos. b) Calcula la arista b del bloque B. b a = 10,0 cm B Madera Madera A A (a) (b) Figura 3 8)Un líquido de densidad 1000 kg/m3 se mueve a razón de 3,0 mm/seg por un tubo horizontal de v1 2,0 cm de diámetro en la sección 1 como muestra la Figura 4. En la sección 2 el tubo reduce su diámetro a 0,50 cm. S1 a) Calcula la velocidad del líquido en la sección 2. b) Calcula la diferencia de presión entre las sección 1 y 2. v2 S2 Figura 4 9) Una esfera hueca de radio interior 9,00 cm y radio exterior 10,0 cm, flota en un líquido de densidad 800 kg/m3 sumergido la mitad de su volumen. a) Calcular la densidad del material que está hecha la esfera b) ¿Cuál sería la densidad de un líquido en el que la esfera flotara sumergida por completo? Vol esfera= 4/3 R3 10) Un bloque de masa m se conecta a un resorte (k = 500 N/m) oscila con MAS sobre una superficie horizontal sin rozamiento. Posee una frecuencia angular de 10 rad/s y una amplitud de 4,0 cm. En t = 0, el resorte está en x = - 4,0 cm. a) Calcula el periodo del movimiento. b) Calcula la masa del bloque. c) Expresar la ecuación de movimiento del bloque, si en el instante inicial el mismo se encuentra a -4,0 cm de la posición de equilibrio. d) Calcular la energía cinética del bloque cuando el mismo pasa por la posición de equilibrio. 2 11) Una cuerda de guitarra vibra con una frecuencia de 440 Hz. El centro de la cuerda se mueve con movimiento armónico simple de amplitud 3,0 mm y constante de fase (fase inicial) cero. a) Escriba la ecuación de movimiento de la posición del centro de la cuerda en función del tiempo. b) ¿Qué magnitud máxima tienen: la velocidad y la aceleración del centro de la cuerda? 12) En la Figura 5 se observa una esfera maciza flotando dentro de un recipiente lleno de líquido, unida, mediante una cuerda inextensible y de masa despreciable, a un cilindro sumergido. La esfera tiene sumergida la mitad de su volumen. El líquido tiene una densidad = 1,04 g/cm 3. El volumen de la esfera es V1 = 0,500 m3 y su densidad es 120 kg/m3. El cilindro tiene una densidad de 3040 kg/m3. Calcula: a) El volumen V2 del cilindro. b) La tensión de la cuerda. 13) La canilla de la Figura 6 tiene una sección A de 2,0 cm² y por ella circula agua con un caudal volumétrico de 12 litros por minuto. Si el chorro tiene una longitud h = 45 cm, calcula la sección inferior B del mismo. V1 A h V2 Figura 5 B Figura 6 3







