unidad11_fisicanuclear - Las cosas que me interesan

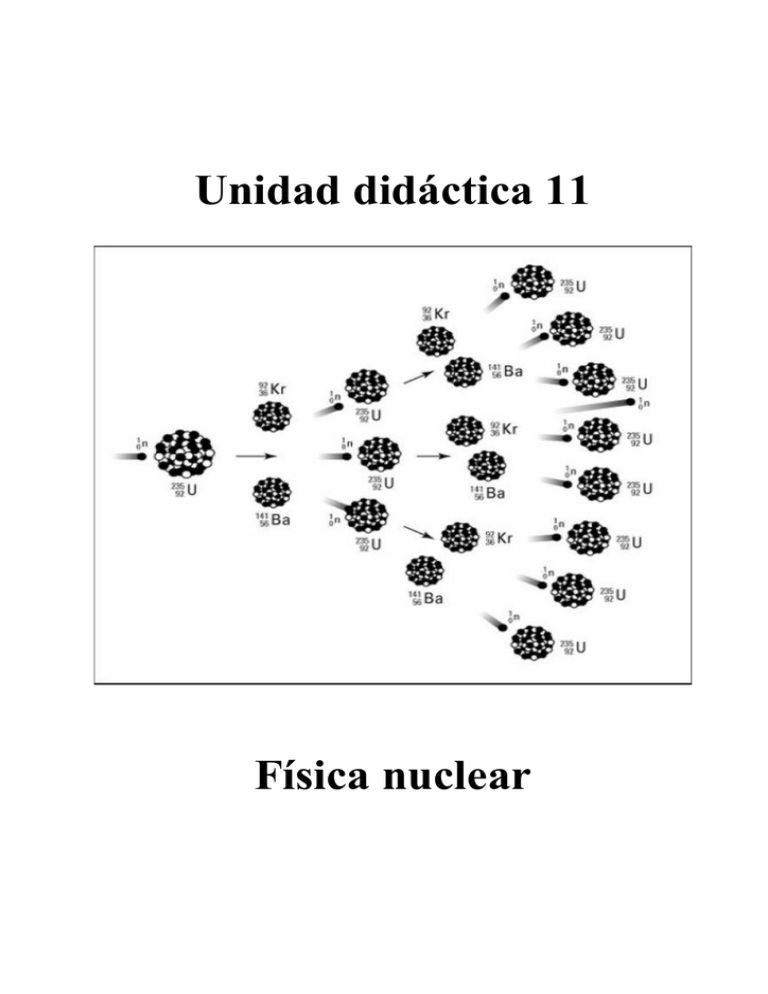
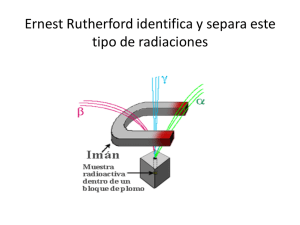
Unidad didáctica 11
Física nuclear
1.- Conceptos básicos.
•
Átomo: es la cantidad de materia más pequeña que conserva sus propiedades. El átomo
está formado por dos partes: núcleo y corteza. El núcleo es muy pequeño comparado con el
átomo en su conjunto y en él está concentrada casi toda la masa del átomo. Las partículas
que se encuentran en el núcleo se llaman nucleones.
•
Protón, (p+): tiene carga eléctrica positiva y una masa igual a la del neutrón pero 1840
veces mayor que la del electrón.
•
Neutrón, (n0): no tiene carga eléctrica y su masa es igual que la del protón.
•
Electrón, (e-): tiene carga eléctrica negativa y una masa 1840 veces más pequeñas que el
protón. Se encuentra girando alrededor del núcleo del átomo a distintas distancias del
mismo, llamadas niveles energéticos u órbitas. Se encuentra en la corteza
•
Elemento: está formado por átomos que tienen el mismo número de protones. El número de
protones que tiene el átomo determina los distintos tipos de los elementos químicos que
existen en la naturaleza. Por ejemplo, si tiene un protón la sustancia se llama hidrógeno; si
tiene dos se llama helio; si tiene 3 protones se llama litio, etc.
•
Número atómico (Z): es el número de protones que tiene un átomo. Dado que el átomo es
neutro, el número de protones tiene que ser igual al número de electrones, para que se
igualen las cargas eléctricas de distinto signo.
Z = nº de protones = nº de electrones.
•
Número másico (A): es igual a la suma del número de protones y el número de neutrones.
Nos da una idea de la masa del átomo. En general, en los átomos ligeros el número de
neutrones suele coincidir con el de protones, pero en los átomos pesados el número de
neutrones suele ser mucho mayor.
A = nº de protones + nº de neutrones.
Para facilitar el trabajo, los átomos se representan utilizando su número atómico Z, su número
másico A y su símbolo:
A
Z
X . Por ejemplo:
16
8
O
•
Isótopos son aquellos átomos de un mismo elemento químico que teniendo igual el número
de protones tienen distinto el número de neutrones. Es decir, los isótopos tienen igual Z y
distinto A; como poseen el mismo número atómico poseen el mismo símbolo químico.
•
Ión: es un átomo con carga eléctrica. Catión: átomo que ha perdido electrones y queda
cargado positivamente. Anión átomo que ha capturado electrones y queda cargado
negativamente.
•
Unidad de masa atómica, u: es la doceava parte de la masa del átomo de carbono-12.
1 u = 1’67 · 1027 kg.
•
Masa atómica relativa de un átomo: es el número de veces que la masa de ese átomo es
mayor que la unidad de masa atómica, es decir, que la doceava parte de la masa del átomo
de carbono-12.
Unidad didáctica 11: Física nuclear
pag. 1
2.- Fuerza nuclear fuerte.
Los nucleones se encuentran a distancias muy cortas unos de otros, por tanto la fuerza repulsiva
entre los protones debería desestabilizar el núcleo, pero esto no sucede porque la fuerza eléctrica
se equilibra con una fuerza atractiva llamada fuerza nuclear fuerte, que se caracteriza por:
•
•
•
Es una fuerza atractiva, de corto alcance, unos 10-15 m. Longitud conocida como Fermi.
Su intensidad es muy alta, cien veces mayor que la de la fuerza electromagnética.
No depende de la carga. Actúa igual entre protones, entre neutrones y entre protones y
neutrones.
Pese a la interacción fuerte, un núcleo puede ser inestable y desintegrarse espontáneamente por
radiactividad, o fisionarse, rompiéndose en fragmentos. Es propio de núcleos pesados, como el
del uranio.
En el núcleo, existe también la fuerza nuclear débil, responsable de la desintegración beta. Las
dos fuerzas nucleares, junto con la gravitatoria y la electromagnética constituyen las cuatro
fuerzas fundamentales de la naturaleza.
2.1.- Estabilidad Nuclear.
La formación de los núcleos y su cohesión interna están directamente relacionadas con las
fuerzas que actúan entre protones y neutrones.
La estabilidad nuclear es el equilibrio entre las fuerzas de repulsión eléctrica de los protones y
la fuerza atractiva nuclear de corto alcance, que experimentan los protones y neutrones del
núcleo. La relación entre el número de protones (Z) y neutrones (N) es clave para la estabilidad
del núcleo. Como la interacción fuerte se satura o agota con los nucleones más próximos, pero
la repulsión eléctrica afecta a todo el núcleo, los núcleos pesados son inestables.
En la gráfica se representan los valores de N y Z para los
núcleos estables de la naturaleza. Los núcleos ligeros tienen
N aproximadamente igual a Z, es decir la relación N/Z =1,
por lo que son estables. Pero, a medida que se hacen más
pesados, se tiende a que N > Z para garantizar que la fuerza
nuclear fuerte contrarreste la repulsión electrostática. La
relación N/Z puede llegar a ser de hasta 1’56, desviándose
del valor 1 en el que el núcleo es estable. Los núcleos que
están fuera del cinturón de estabilidad son radiactivos. No
hay núcleos estables con Z > 83.
Tanto en núcleos pesados como ligeros existe otra causa de inestabilidad nuclear que depende de
la interacción débil. Es la tendencia de neutrones y protones a intercambiarse dando lugar a
emisiones β+, β- y a la captura electrónica:
•
Emisión β-:
1
0
•
•
1
1
p+
Emisión β :
1
1
p
1
0
n + e (positrón) + ν (neutrino)
Captura electrónica:
1
1
p + −01 e
+
0
−1
e + ν (antineutrino)
n
0
1
1
0
n +ν
Los antineutrinos y neutrinos son casi indetectables. Uno es la antipartícula o antimateria del
otro. El positrón es la antipartícula del electrón.
Unidad didáctica 11: Física nuclear
pag. 2
3.- Defecto de masa y energía de enlace.
Experimentalmente se sabe que la masa de cualquier núcleo siempre es inferior a la suma de las
masas de los nucleones que lo forman. Esta pérdida de masa se llama defecto de masa, Δm:
Δm = Z . mp + N . mn - m
Donde N es el número de neutrones, mp y mn, son respectivamente las masas de un protón y un
neutrón y m es la masa nuclear.
El equivalente en energía del defecto de masa, que se libera cuando se forma un núcleo, recibe el
nombre de energía de enlace. Esta energía que se desprende indica que el núcleo es más estable
que sus partículas libres porque tiene menos energía.
La energía de enlace o de ligadura, Ee, de un núcleo, es la energía liberada en la formación de
éste a partir de los nucleones libres, o la necesaria para disgregar un núcleo y separar sus
nucleones.
Para calcular esta energía, se usa la ecuación de Einstein que relaciona masa y energía: E=m · c2.
Donde c = 3 · 108 m/s
Aplicándola a la energía de enlace se obtiene: Ee = ΔE = Δm · c2 y, por tanto:
Ee = (Z · mp + N · mn - m) · c2
La energía de los procesos nucleares es mucho mayor que la que corresponde a los procesos
químicos ordinarios, por eso se utiliza una nueva unidad de energía, que no es del sistema
internacional, el Mega-electrón-Voltio (MeV). 1 MeV = 1´6 · 10-13 J
3.1.- Energía de enlace por nucleón.
Para calcular la intensidad con que es retenido cada nucleón dentro del núcleo, se emplea la
energía de enlace nuclear por nucleón, que es la energía media que se debe suministrar a un
núcleo para arrancarle uno de sus nucleones:
E
En = e
A
Un núcleo será tanto más estable cuanto mayor sea la energía que hay que darle para que los
nucleones dejen de estar ligados entre sí. Esta energía coincide con la que se libera cuando se
forma el núcleo a partir de los nucleones libres.
Al analizar la gráfica, que representa como varía la energía de enlace por nucleón frente al
número másico, se observa:
• En los núcleos ligeros se produce un aumento
brusco de la energía de enlace frente al número
másico.
Existiendo núcleos especialmente
estables como los de He, C y O.
•
Para elementos con número másico > 20 la
energía de enlace por nucleón es de
aproximadamente 8’5 MeV.
Unidad didáctica 11: Física nuclear
pag. 3
•
Entre los números másicos 40 y 80, los valores de energía son máximos, esto quiere decir
que los núcleos correspondientes son los más estables, siendo, en la naturaleza, el más
estable de todos, el núcleo de hierro con número másico 56.
•
Las variaciones de energía de enlace por nucleón son pequeñas para números másicos
superiores a 20. Este hecho significa que la fuerza nuclear no aumenta al hacerlo el número
de nucleones. La fuerza nuclear se ejerce entre los nucleones más próximos y es
independiente del número total de nucleones. Esta característica de la fuerza nuclear se
llama saturación.
•
En la zona central, la energía de enlace por nucleón da unos valores prácticamente
constantes. Sin embargo, existen dos zonas de menor estabilidad nuclear, correspondientes a
núcleos ligeros y a núcleos pesados, con valores menores de esta energía. Por tanto, las dos
formas de ganar energía por nucleón en una reacción nuclear, y por lo tanto pasar a una
situación más estable, con el consiguiente desprendimiento de energía, son la fisión de un
núcleo pesado en dos más ligeros de la zona central o la fusión de dos núcleos ligeros para
dar uno más pesado, más próximo a esa zona central.
4.- Desintegración radiactiva.
En 1896 Henry Becquerel descubrió que una sal de uranio velaba un papel fotográfico y llamó a
este fenómeno radiactividad. Posteriormente, Marie Curie comprobó que otros elementos
pesados como el radio y el polonio también emitían radiactividad.
La radiactividad, es un proceso de desintegración espontánea de núcleos pesados inestables en
núcleos más ligeros, por emisión de radiación. Es una propiedad característica del núcleo.
4.1.- Tipos de radiaciones.
En la desintegración radiactiva se emiten tres tipos de radiaciones que se caracterizan por su
poder de penetración en la materia y por ionizar el aire, es decir, convertir en iones las moléculas
del aire. Estas radiaciones son:
•
Radiación alfa, α: constituida por núcleos de helio
( 42 He ). Su velocidad es del orden del 5 % de la de la
luz. Es un tipo de radiación poco penetrante que
puede ser detenida por una simple hoja de papel o unos
centímetros de aire, pero, por su elevada masa, poseen
gran capacidad de ionizar la materia que atraviesa.
•
Radiación beta, β: está constituida por electrones ( −01 e ). Su velocidad puede ser el 99’95 %
de la de la luz. Su poder de penetración es algo mayor que el de la radiación α, pues se
necesitan metros de aire, una lámina de aluminio o unos centímetros de agua para detenerla.
Sin embargo, al ser más ligeras, esta radiación es menos ionizante.
•
Radiación gamma, γ: es radiación electromagnética constituida por fotones muy
energéticos. Tiene un poder de penetración muy alto, atraviesa el cuerpo humano y sólo se
frena con planchas de plomo y muros gruesos de hormigón. Pero su capacidad de ionización
es baja. Al ser tan penetrante y tan energética, es la más peligrosa de las tres.
Unidad didáctica 11: Física nuclear
pag. 4
4.2.- Procesos radiactivos.
Para tratar de explicar los procesos de desintegración de átomos radiactivos Rutherford y Soddy
propusieron, en 1902, la siguiente hipótesis:
Cuando un núcleo emite radiación α o β, se transforma en otro elemento químico diferente, se
dice que el núcleo se ha transmutado o desintegrado.
4.3.- Leyes de Soddy y Fajans o de los desplazamientos radiactivos.
•
1ª ley de los desplazamientos radiactivos o desintegración α.
Cuando un núcleo emite una partícula α, ( 42 He +2 ), se transforma en otro núcleo diferente, cuyo
número másico es cuatro unidades menor, y cuyo número atómico es dos unidades menor que el
núcleo de partida:
A
Z
Ejemplo:
•
235
92
A−4
Z−2
Y + 42 He
X
231
90
Th + 42 He
U
2ª ley de los desplazamientos radiactivos o desintegración β−.
Cuando un núcleo emite una partícula β ( −01 e ), su numero másico no varía pero su número
atómico aumenta en una unidad.
A
Z
Ejemplo:
210
83
Bi
210
84
A
Z+1
Y+
X
Po +
0
−1
0
−1
e + antineutrino (ν )
e
Algunos núcleos pueden emitir otra partícula, el positrón, 01 e, que procede de la desintegración
β+ de un protón del núcleo. Cuando un núcleo emite una partícula β+, ( 01 e ), su numero másico
no varía pero su número atómico disminuye en una unidad.
A
Z
Ejemplo:
•
30
15
P
30
14
X
Y + 01 e + ν (neutrino)
A
Z−1
Si + 01 e
3ª ley de los desplazamientos radiactivos o desintegración gamma, γ.
En este tipo de desintegración el núcleo no pierde su identidad. Mediante esta radiación el
núcleo se desprende de la energía que le sobra para pasar de un estado excitado a otro estado de
energía más baja o estado fundamental. Los rayos gamma son fotones muy energéticos. Este
tipo de emisión acompaña tanto a las radiaciones alfa como a las radiaciones beta. Es una
radiación muy penetrante.
*
A
A
ZX
ZX + γ
Unidad didáctica 11: Física nuclear
pag. 5
4.4.- Series Radiactivas.
Cuando un núcleo se va desintegrando, emite radiación y da lugar a otro núcleo distinto que
también puede ser radiactivo y emitirá, a su vez, nuevas radiaciones. El proceso continuará hasta
que aparezca un núcleo estable, no radiactivo. Todos los núcleos que proceden del inicial
(núcleo padre) hasta llegar a otro estable, forman una serie o cadena radiactiva.
Se
conocen
cuatro
series
radiactivas, tres de las cuales
existen en la naturaleza ya que
proceden de núcleos radiactivos
primigenios, que son aquellos que
sobreviven en la Tierra desde su
formación. Esto se debe a que su
semivida es comparable a la edad
de la Tierra.
A
Cadena del
4n
4n+1
Series radiactivas
Padre Semivida (años) Producto final
Torio
232
90
Th
1'41.1010
208
82 Pb
Neptunio
237
93
Np
2’14.106
209
82
Pb
4n+2 Uranio-Radio
238
92 U
4’51.109
206
82
Pb
4n+3 Uranio-Actinio
235
92 U
7’18.108
207
82
Pb
La otra serie radiactiva es la del Np-297, que se había extinguido, pero que, con las pruebas
nucleares realizadas en los últimos años, ha vuelto aparecer. En cada serie todos los núcleos
están relacionados, en la del Th-232, por ejemplo, todos los núcleos de la serie tienen números
másicos iguales a 4n, siendo n un número entero cualquiera.
4.5.- Ley de desintegración radiactiva
En 1902 Ernest Rutherford y Frederick Soddy, sugirieron que el ritmo con que una sustancia
radiactiva emite partículas radiactivas disminuye exponencialmente con el tiempo. La
desintegración de un núcleo cualquiera se produce al azar, y el número de núcleos que se
desintegran en un tiempo, t, es directamente proporcional al tiempo y al número de núcleos
existentes. Su expresión matemática es:
N = N 0 ⋅ e − λ⋅t
Donde N es el número de núcleos que quedan sin desintegrar después de un tiempo t, N0 es el
número de núcleos iniciales y la constante, λ, es la constante de desintegración o constante
radiactiva, que tiene un valor característico para cada sustancia radiactiva y mide la
probabilidad, por unidad de tiempo, de que los núcleos pertenecientes a esa población se
desintegren.
4.6.- Semivida o periodo de semidesintegración, T1/2, es el tiempo que tarda una muestra
radiactiva en reducirse a la mitad.
ln 2
T1 =
2
λ
4.7.- Actividad radiactiva o velocidad de desintegración, A: es el número de desintegraciones
que se producen por unidad de tiempo. Unidad: Becquerelio, Bq. 1 Bq=1 d.p.s (desintegración
por segundo)
A = λ⋅N
Como la actividad, A, y la masa, m, de una sustancia radiactiva son directamente proporcionales
al número de núcleos, N, también se cumple que:
y
A = A 0 ⋅ e − λ⋅t
m = m 0 ⋅ e − λ⋅t
Donde A0 es la actividad inicial y A la actividad a cabo de un tiempo t. De la misma forma, m0
es la masa inicial y m, la masa cuando ha transcurrido un tiempo t.
Unidad didáctica 11: Física nuclear
pag. 6
5.- Datación de muestras con fuentes radiactivas.
En 1949, W. F. Libby publicó los resultados de las primeras dataciones realizadas con el método
del carbono-14, un isótopo radiactivo natural del carbono descubierto en 1940.
El elemento carbono presenta tres isótopos distintos: 12C (el más abundante), 13C y 14C. Los dos
primeros no son radiactivos, pero el tercero se desintegra de forma espontánea, emitiendo
partículas β (desintegración β-):
14
14
+ −01 β
6C
7N
El 146 C se origina de forma continua en las capas altas de la atmósfera, al incidir neutrones
procedentes de la radiación cósmica con átomos de nitrógeno:
14
7
N + 01 n
14
6
C + 11 p
Este isótopo del carbono, al igual que el otro isótopo, 12C, se
combina con el oxígeno y forma CO2. Los seres vivos
intercambian continuamente CO2 con la atmósfera, de forma que
mientras están vivos mantienen constante la proporción de
14 12
C/ C, y su composición isotópica es la misma que la de la
atmósfera que le rodea (en cada gramo de carbono de nuestro
cuerpo hay suficiente 14C para que se produzcan 15 emisiones beta
por minuto).
Cuando el organismo muere, cesa este equilibrio y la desintegración del 14C no es compensada
con el carbono atmosférico. La cantidad de 14C va disminuyendo con el tiempo, por lo que basta
medir el número de desintegraciones que se producen por gramo de carbono, es decir, la
actividad de la muestra, para determinar la fecha en la que murió un organismo determinado.
El isótopo 14C tiene un periodo de semidesintegración (T1/2) de 5730 años, lo que lo hace muy
adecuado para fechar objetos, de origen orgánico, de hasta 25.000 años de antigüedad.
Otros isótopos, con T1/2 más grandes, se usan para fechar periodos de tiempos mayores. La serie
radiactiva del 238U, por ejemplo, se puede usar para determinar la edad de las rocas de la Tierra.
El método consiste en hallar la razón entre el 238U y su producto final, el 206Pb.
6.- Reacciones nucleares: Fisión y fusión.
Las reacciones nucleares son procesos en los que intervienen directamente los núcleos
atómicos transformándose en otros distintos.
En toda reacción nuclear se cumplen los siguientes principios de conservación:
•
Conservación del número de nucleones: la suma de lo números másicos de los reactivos es
igual a la suma de los números másicos de los productos.
•
Conservación de la carga eléctrica: la suma de los números atómicos de los reactivos
coincide con la suma de los números atómicos de los productos.
•
Conservación de la cantidad de movimiento: la cantidad de movimiento total de los
reactivos es igual a la de los productos.
Unidad didáctica 11: Física nuclear
pag. 7
•
Conservación de la masa-energía: la diferencia entre las masa de reactivos y productos se
transforma en energía según el principio de equivalencia masa-energía: ΔE = Δm · c2
Ejemplo:
14
7
17
8
N + 42 He
O + 11 H
Otra forma de representar la ecuación: 147 N (α,p) 178 O. Dentro del paréntesis están las partículas
incidente y emergente. A la izquierda del paréntesis está el núcleo inicial y a la derecha, el final.
6.1.- Fisión nuclear.
La fisión nuclear es un proceso en el que un núcleo pesado se divide en otros más ligeros de
tamaño variable. Se produce cuando se bombardean núcleos pesados con neutrones.
Ejemplo:
235
92
U + 01 n
141
56
Ba +
92
36
Kr + 3 01 n
Los neutrones producidos en la fisión reaccionan con otros núcleos de uranio y el número de
neutrones aumenta de forma exponencial. Se origina una reacción nuclear en cadena, que
libera una gigantesca cantidad de energía. Si se descontrola el proceso, habrá una explosión
nuclear (bomba atómica); pero si se controla el número de neutrones, utilizando una sustancia
llamada moderador que los absorbe, la energía producida se puede mantener constante y el
proceso puede ser usado en un reactor nuclear para producir electricidad.
6.2.- Fusión nuclear.
Fusión nuclear es un proceso por el que dos núcleos de número másico bajo se combinan para
formar un núcleo más pesado con mayor energía de enlace por nucleón. La energía producida
en las estrellas tiene su origen en la reacción de fusión del hidrógeno:
4 11 H
4
2
He + 2 +01 e + 24’7 MeV
La bomba de hidrógeno se basa en la siguiente reacción: 21 H + 31 H
4
2
He + 01 n + 17’6 MeV
Aunque las reacciones de fusión nuclear podrían ser una importante fuente de energía, las
altísimas temperaturas y presiones que se requieren para conseguir que los núcleos superen la
repulsión eléctrica y lleguen a unirse, hacen el proceso técnicamente inviable de momento.
Unidad didáctica 11: Física nuclear
pag. 8
Resumen de fórmulas de Física nuclear
Emisión β-
1
0
n
1
1
p+
Emisión β+
1
1
p
1
0
n + 01 e (positrón) + ν (neutrino)
Captura electrónica
1
1
p + −01 e
Desintegración α o 1ª ley de los
desplazamientos radiactivos
A
Z
X
A
Z
X
A
Z+1
A
Z
X
A
Z−1
A
Z
X*
Desintegración β− o 2ª ley de los
desplazamientos radiactivos
Emisión de un positrón
Desintegración, γ o 3ª ley de los
desplazamientos radiactivos
0
−1
1
0
e + ν (antineutrino)
n +ν
A−4
Z−2
Y + 42 He
Y+
0
−1
e + antineutrino (ν )
Y + 01 e + ν (neutrino)
A
Z
X+γ
Defecto masa formación de un núcleo
Δm = Z . mp + N . mn - m
Defecto masa en un reacción nuclear
Δm =
Energía de enlace
Ee = ΔE = Δm · c2
Energía de enlace por nucleón
En =
∑ reactivos − ∑ productos
Ee
A
N = N 0 ⋅ e − λ⋅t
Ley de desintegración radiactiva
m = m 0 ⋅ e − λ⋅t
Semivida o periodo de semidesintegración
T1 =
2
14
7
N + 01 n
Desintegración del C-14
14
6
C
14
6
14
7
C + 11 p
N + −01 β
Fisión nuclear
235
92
Fusión nuclear en las estrellas
4 11 H
Fusión nuclear bomba de hidrógeno
2
1
Unidad didáctica 11: Física nuclear
λ
A = λ⋅N
A = A 0 ⋅ e − λ⋅t
Actividad radiactiva o velocidad de
desintegración
Formación del C-14
ln 2
U + 01 n
H + 31 H
141
56
4
2
Ba +
92
36
Kr + 3 01 n
He + 2 +01 e
4
2
He + 01 n
pag. 9
Problemas
1.- El cloro natural está formado por un 75 % de
atómica del cloro natural.
35
17
Cl y un 25 % de
37
17
Cl. Calcula la masa
2.- La energía de enlace del núcleo de 42 He es 28’296 MeV. Calcula la energía, expresada en
Julios, que se desprende cuando se forman 0’5 g de helio a partir de protones y neutrones que se
encuentran libres. mHe = 4’002603 u, NA = 6’023.1023 núcleos /mol
3.- La energía de enlace de los núcleos 105 B, 115 B, 125 B son respectivamente 64’751, 76’205 y
79’575 MeV. a) Calcula la energía de enlace por nucleón. b) Justifica cuál de los núcleos
anteriores es más estable.
4.- Sabiendo que el oxígeno 16 tiene 8 protones en su núcleo y su masa atómica es 15’9949 u,
calcula: a) Su defecto de masa. b) La energía de enlace en julios. c) La energía de enlace por
nucleón también en julios. mp =1’0073 u, mn =1’0087 u, 1 u =1’67·1027 kg, c =3·108 m/s
5.- Calcula el defecto de masa y la energía de enlace por nucleón, que se produce al formarse los
núcleos de 42 He y 31 H (tritio). Datos: mnuclear He-4 = 4’001506 u, mnuclear H-3 = 3’015501 u, mp =
1’007276 u, mN= 1’008665 u.
6.- Completa las siguientes desintegraciones:
234
a) 238
92 U
90 Th + …
b)
210
83
c)
238
86
Bi
210
84
Po + …
Rn
234
84
Po + …
7.- El 233
92 U se desintegra en Th emitiendo una partícula α. El núcleo que se obtiene emite
también una partícula α, desintegrándose en otro de Ra que, a su vez emite una partícula β y se
transforma en un núcleo de Ac. Escribe las correspondientes ecuaciones nucleares.
8.- Indica el tipo de emisión que tiene lugar en los procesos radiactivos siguientes:
137
22
22
241
237
a) 137
10 Ne c)
95 Am
93 Np
55 Cs
56 Ba b) 11 Na
9.- Completa las reacciones nucleares: a) 73 Li (p, …) 74 Be, b)
19
9
F(p,α) …, c) 63 Li(… ,p) 73 Li
10.- La actividad inicial de una sustancia radiactiva es 7’91.1016 Bq y el periodo de
semidesintegración es 2’72.106 s. Calcula: a) El número inicial de núcleos. b) el número de
núcleos que quedarán sin desintegrar cuando hayan pasado 5 días. c) La actividad en ese
instante.
11.- Se dispone de una muestra de 80 mg de Rn (λ = 0’182 días-1). Calcula la masa que quedará
al cabo de una semana. b) ¿Cuánto tiempo debe transcurrir para que queden 10 mg?
12.- En una excavación se ha encontrado una herramienta de madera de roble. Sometida a la
prueba del 14C se observa que se desintegran 100 átomos cada hora mientras que una muestra de
madera de roble actual presenta una tasa de desintegración de 600 átomos/hora. Sabiendo que el
periodo de semidesintegración del 14C es de 5730 años, calcula la antigüedad de la herramienta.
Unidad didáctica 11: Física nuclear
pag. 10
13.- La actividad de 14C de un resto arqueológico es de 60 desintegraciones por segundo. Una
muestra actual de idéntica composición e igual masa posee una actividad de 360
desintegraciones por segundo. El periodo de semidesintegración del 14C es de 5700 años.
a) Explique a qué se debe dicha diferencia y calcule la antigüedad de la muestra arqueológica.
b) ¿Cuántos núcleos de 14C tiene la muestra arqueológica en la actualidad? ¿Tienen las dos
muestras el mismo número de átomos de carbono? Razone las respuestas.
14.- Una muestra de 80 g de 60Co, tiene una constante de desintegración de 2·10-6 s-1.
a) Determina el periodo de semidesintegración de este núclido. b) Determina el tiempo que ha
de transcurrir para que la muestra quede reducida a 60 g. c) Determina la actividad inicial de la
muestra. Datos: NA = 6’023·1023, MCo = 59’93 u.
15.- a) En la reacción del 63 Li con un neutrón se obtiene un núclido X y una partícula α. Escriba
la reacción nuclear y determine las características del núclido resultante.
4
b) Calcule la energía liberada en la reacción de fusión: 21 H + 21 H
2 He
c = 3 · 108 ms-1, 1 u = 1’66 · 10-27 kg, m 42 He = 4’0026 u, m 21 H = 2’0141 u
1
133
99
1
16.- Dada la reacción nuclear: 235
92 U + 0 n
31 Sb + 41 Nb + 4 0 n
a) Explique de qué tipo de reacción se trata y determine la energía liberada por átomo de uranio.
6
b) ¿Qué cantidad de 235
92 U se necesita para producir 10 kWh?
Datos: c= 3·108 ms-1, NA= 6’023·1023 mol-1, mU= 235’124 u, mSb= 132’942 u, mNb= 98’932 u,
mn = 1’0086 u, 1 u = 1’66 · 10-27 kg
Unidad didáctica 11: Física nuclear
pag. 11
Problemas de selectividad
222
1.- (Junio 2005) El 226
88 Ra se desintegra radiactivamente para dar 86 Rn. a) Indique el tipo de
emisión radiactiva y escriba la correspondiente ecuación. b) Calcule la energía liberada en el
proceso. c =3.108 m s–1; mRa =225,9771 u; mRn =221,9703 u; mHe =4,0026 u ; 1 u =1,67.10–27 kg
2.- (Junio 2006) El período de semidesintegración del 226Ra es de 1620 años.
a) Explique qué es la actividad y determine su valor para 1 g de 226Ra.
b) Calcule el tiempo necesario para que la actividad de una muestra de 226Ra quede reducida a un
dieciseisavo de su valor original. NA = 6,02 · 1023 mol-1
3.- (Junio 2007) a) La masa de un núcleo atómico no coincide con la suma de las masas de las
partículas que los constituye. ¿Es mayor o menor? ¿Cómo justifica esa diferencia?
b) ¿Qué se entiende por estabilidad nuclear? Explique cualitativamente la dependencia de la
estabilidad nuclear con el número másico.
4.- (Junio 2008) La masa atómica del isótopo 147 N es 14’0001089 u. a) Indique los nucleones de
este isótopo y calcule su defecto de masa. b) Calcule su energía de enlace.
c = 3.108 ms-1, 1 u = 1’67.10-27 kg, mp = 1’007276 u, mN = 1’008665 u
5.- (Junio 2009) a) Explique el origen de la energía liberada en una reacción nuclear basándose
en el balance de masa-energía. b) Dibuje aproximadamente la gráfica que relaciona la energía de
enlace por nucleón con el número másico y, a partir de ella, justifique por qué en una reacción de
fisión se desprende energía.
6.- (Junio 2010) a) Estabilidad nuclear. Explique el origen de la energía liberada en los procesos
de fisión y fusión nucleares.
7.- (Junio 2011) La fisión de un átomo de
235
92
U se produce por captura de un neutrón, siendo los
144
56
productos principales de este proceso Ba y 90
36 Kr.
a) Escriba y ajuste la ecuación nuclear correspondiente y calcule la energía desprendida por cada
átomo que se fisiona.
b) En una determinada central nuclear se liberan mediante fisión 45 · 108 W. Determine la masa
del material fisionable que se consume cada día.
c = 3.108 ms-1, 1 u = 1’7.10-27 kg, mU = 143’92 u, mKr= 89’94 u, mn= 1’008665 u
8.- (Junio 2012) Entre unos restos arqueológicos de edad desconocida se encuentra una muestra
de carbono en la que sólo queda una octava parte del carbono 14C que contenía originalmente. El
periodo de semidesintegración del 14C es de 5730 años.
a) Calcule la edad de dichos restos.
b) Si en la actualidad hay 1012 átomos de 14C en la muestra, ¿cuál es su actividad?
Unidad didáctica 11: Física nuclear
pag. 12