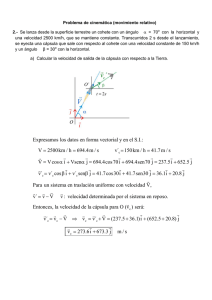
θ Bm v = 1 m / s 3 k g / s

Departamento de Fı́sica Aplicada a los Recursos Naturales. E.T.S.I. de Minas. U.P.M.
FÍSICA BÁSICA
CURSO 1o . INGENIERO GEÓLOGO
Segundo cuatrimestre
Ejercicios y problemas
Curso 2006/2007
Aplicaciones de las leyes del movimiento
21. Un globo de masa m desciende verticalmente con una aceleración constante a. Determine qué masa de lastre debe
arrojarse del globo para que éste vuelva a ascender con la misma aceleración a.
w
q
22. Un bloque de masa m se apoya sobre una superficie cónica lisa, de ángulo θ, y gira con
velocidad angular constante alrededor del eje del cono, manteniéndose la varilla de longitud
l que lo sujeta constantemente paralela a la superficie lateral del cono. Determı́nese: a) la
velocidad lineal del bloque B, b) la acción de la superficie del cono sobre B y la tensión de
la varilla, c) la velocidad angular necesaria para que el bloque se despegue del cono.
l
m
B
a
23. Una taza semiesférica de radio a gira alrededor de su eje vertical con velocidad
angular constante ω. Si se coloca una bola de masa m en la taza giratoria, se encontrará, finalmente, en un punto a una distancia d del eje. Determı́nese d en función de
ω.
w
m
d
24. Sobre la cinta transportadora de la figura se deposita arena a razón constante de 3 kg/s. Se quiere
3 k g /s
v = 1 m /s
mantener dicha cinta con velocidad constante v = 1
m/s. Determı́nese que fuerza es necesario aplicar a la
cinta.
25. Un partı́cula de uranio de masa inicial m0 y velocidad inicial v0 se mueve rectilı́neamente libre de fuerzas mientras
se desintegra según la expresión m = m0 exp(−γt), siendo γ la constante de desintegración. Determine su velocidad
en función del tiempo.
26. Suponiendo una órbita circular, estimar el momento angular de la tierra entorno al sol. Datos: masa de la tierra
5,98 × 1024 kg, radio de la órbita de la tierra 1,49 × 1011 m.
27. Una masa m, atada al extremo de una cuerda, está sostenida por un plano
liso horizontal y se mueve con velocidad v según una trayectoria circular de
radio r. Tirando de la cuerda por el extremo inferior, el radio de la trayectoria
se reduce a r/2. Determinar la nueva velocidad de la masa y las tensiones inicial
y final de la cuerda.
r
v
m
28. Un cohete de 103 kg se coloca verticalmente sobre su base de lanzamiento. El gas de propulsión se expele a una
razón de 20 kg/s. Encontrar la velocidad mı́nima de los gases de escape de modo que el cohete comience a elevarse.
29. Un cohete, lanzado verticalmente, expele los gases a una razón constante de 5 × 10−2 m0 kg/s, donde m0 es su
masa inicial. La velocidad de escape respecto del cohete es de 5 × 103 m/s. Encontrar la velocidad del cohete al cabo
de 10 s.
30. Una cadena flexible de longitud L y peso P está colocada
inicialmente en reposo sobre una superficie sin fricción ABC, esL -a
tando D a una distancia L − a de B. Demostrar que cuando el
a
extremo B llega al punto B la velocidad de la cadena es
p
D
A
B
v = (g/L)(L2 − a2 )senα
a
C
.
31. Cuando la tierra se encuentra en el afelio (la posición más alejada respecto del sol), en 21 de junio, su distancia
es de 1,52 × 1011 m y su velocidad orbital es de 2,93 × 104 m/s. Encontrar su velocidad orbital en el perihelio (la
posición más cercana al sol), seis meses más tarde, cuando su distancia del sol es 1,47 × 1011 m. Encontrar también
las velocidades radial y transversal de la tierra en ambas posiciones, asi como la velocidad angular de giro.