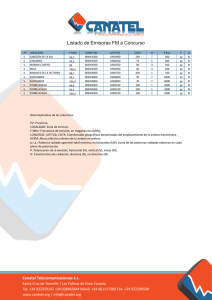
Mecánica
Anuncio

Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 1.- ECUACIONES DE DIMENSIONES 1.1) Entre las distintas formas de expresar un trabajo en Física se encuentran las siguientes: Ec = energía cinética = ½ mv2 Ep = energía potencial = mgh T = trabajo termodinámico = pV Siendo: m = masa; g = aceleración de la gravedad; h = altura; p = presión; V = volumen. Demostrar que, en efecto, a todas ellas corresponde la misma ecuación dimensional. 1.2) La fórmula que relaciona la distancia entre dos capas de un fluido h, la velocidad v, la sección A y la fuerza F, es F = η A. v h siendo η el coeficiente de viscosidad. Se pide la ecuación de dimensiones de η. 1.3) La ley de Newton, que da la fuerza de atracción de dos masas en función de la distancia, está expresada por la ecuación F=G m.m' d2 Hallar las dimensiones de la constante G. 1.4) Suponiendo que el periodo de oscilación de un péndulo simple (T = tiempo que tarda en dar una oscilación) depende exclusivamente de la longitud del hilo (l), de la masa (m) de la partícula que oscila y de la aceleración de la gravedad (g), y que en la fórmula del periodo no intervienen más que las magnitudes indicadas, en producto entre sí (elevadas a exponentes diversos) y ligadas por un coeficiente numérico, deducir las leyes a que obedece el periodo de oscilación de dicho péndulo. 1.- Ecuaciones de dimensiones 1 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 1.5) Sabiendo que la velocidad de salida de un líquido por un pequeño orificio practicado en la pared de una vasija es proporcional a la distancia vertical (h) del centro del orificio a la superficie libre del liquido y a la aceleración de la gravedad (g), dudamos si la velocidad es proporcional también a la densidad del liquido (ρ). Deseamos resolver nuestra duda y hallar la fórmula de la función: V = f(h, g, ρ) 1.6) Deducir mediante análisis dimensional una expresión que relaciona la presión P de un fluido con su densidad ρ y la velocidad de movimiento del mismo. 1.7) Dada la fórmula física que no es correcta ¿cómo la modificarías, para que sí lo fuese? Razonar la respuesta m. a ρ .S = P .l + 1,5 2 l t en donde: m = masa; a = aceleración; l = longitud; P = presión; ρ = densidad; S = superficie; t = tiempo 1.8) Un alumno duda en un examen entre dos expresiones para la fuerza centrífuga a) F = mv2/R; b) F = mω2 R2 ¿Cómo podrá salir de dudas? ¿Cuál es la correcta? 1.9) Demostrar que la fuerza, la velocidad y la aceleración pueden formar un sistema de magnitudes fundamentales para la Mecánica. ¿Qué dimensiones tendrá el volumen, la velocidad angular y la densidad en ese sistema de unidades? 1.- Ecuaciones de dimensiones 2 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 2. CÁLCULO VECTORIAL FORMULARIO Suma de vectores : R = A + B + C R x = Ax + B x + C x R y = Ay + B y + C y R z = Az + B z + C z R = R x2 + R 2y + R z2 Diferencia de vectores : V = A− B V x = Ax − B x V y = Ay − By V z = Az − B z Pr oducto escalar. Es un escalar : A.B = A.B cos α = Ax .B x + A y .B y + Az .B z i j k Pr oducto vectorial. Es un vector : A ∧ B = A B senα = A x Ay Az B x By Bz Momento de un vector respecto a un punto. Es un vector : ( x, y , z) coordenadas del vector A ( x0 , y0 z 0 ) coordenadas del punto O i j k M O A = OA ∧ A = x − x0 y − y0 z − z 0 Ax Ay Az Momento de un vector respecto a un eje. Es un escalar : M e = proy (r ∧ A) (r vector de posición de A respecto a cualquier punto del eje) Si cos α, cos β, cos γ son los cos enos directores del eje : cos α cos β cos γ M e = x − x 0 y − y0 z − z 0 rx 2.- Cálculo vectorial ry rz 3 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería 2.1) Torrelavega La suma de dos vectores A y B es un vector C de módulo 24 y cuyos cosenos directores son 1/3, -2/3, 2/3, además, el vector 3A-2B tiene por componentes 7,9,3. Calcular las componentes de los vectores A y B. Sol. A(23/5, -23/5,7); B(17/5,-57/5,9). 2.2) Entre los cosenos directores de un vector A existen las siguientes relaciones: cosα/cosβ=2/3, cosβ/cosγ=3/4 y el módulo de este vector es la unidad. Calcular el producto vectorial de este vector por el B=√29(i+j+k). Sol. -i+2j-k. 2.3) Dado el vector A de módulo 14 y B de módulo 21, cuyos cosenos directores son respectivamente proporcionales a -2, -3 y 6 y 1,2 y 2. Calcular: 1º) La resultante del sistema, 2º) El momento del vector resultante respecto al punto (1,-1,2); 3º) El momento resultante respecto al eje Z; 4º) El producto vectorial de A∧B; 5º) El producto escalar A.B. Sol. 1º) R=11i+20j+2k. 2º) MoR=-42i+20j+31k. 3º) Mz=31. 4º) A∧B=252i-140j+14k. 5º) A.B=-56. 2.4) Calcular d/dtMoA (O es el origen), siendo A=i-2j+3k y el punto de aplicación de este vector (3t,2,gt2). Sol. 4gti+(2gt-9)j-6K 2.5) siendo: A=ti-2tj+t2k, Calcular: r r d A∧ B r r dt A.B B=i+j+k. 2 Sol. 3(i-k)/(t-1) . 2.6) Un automóvil recorre 5 millas hacia el este, luego 4 millas hacia el sur y por último, 2 millas hacia el oeste. Hállense la magnitud y dirección del desplazamiento resultante. Sol. α = 53,13º E-S. 2.7) El vector M de longitud 5 cm, forma un ángulo de 36,9º en el sentido contrario al giro de las agujas de un reloj sobre el eje + X. Se le suma un vector N y la resultante es un vector de magnitud 5 cm, que forma un ángulo de 53,1º en el sentido contrario a las agujas del reloj con el eje + X. Hállense: a) las componentes de N; b) la magnitud y la dirección de N. Sol. a) (-1,1); b) 1,41 cm, ángulo 135º. 2.- Cálculo vectorial 4 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 2.8) Hállese el ángulo que forman los dos vectores A=3i+4j+5k y B=3i+4j-5k. Sol. 90º. 2.9) Un vector A, de 10 unidades de longitud, forma un ángulo de 30º con un vector B de seis unidades de longitud. Hállese la magnitud del vector diferencia A-B y el ángulo que forma con el vector A. Sol. 5,7; 31,7º. 2.10) Hallar el valor de la expresión A∧ Nc, siendo: A=2i-j+2k; B=i-2j+k y Nc el momento del vector B que está aplicado al punto B(2,3,1) con respecto al punto C(1,1,1). Sol. 6i+12j. 2.11) Hallar el valor de la expresión A∧MoB, siendo A=2i-j+2k, B=i-2j-k, y estando aplicado este último vector en el punto B(1,2,0). Sol. 2i+4j. 2.12) Demostrar que los vectores libres A=i-2j+3k; B=2i+j-2k, C=i+3j-5k pueden formar los lados de un triángulo. 2.13) Demostrar que los vectores A=-2i-3j-k; B=4(i-j+k) son perpendiculares. 2.14) Los tres vértices de un triángulo son: A(2, 1, 3); B(2, -1, 1) y C(0, -2, 1). Calcular: 1) Área del triángulo, 2) Ángulo A Sol. 1) 3 unidades cuadradas, 2) 30º 57’ 49’’ 2.15) Tres vértices de un paralelogramo ABCD tienen por coordenadas: A(2, 0, 2); B(3, 2, 0) y D(1, 2, -1). Calcular: 1) Las coordenadas del vértice C; 2) Área del paralelogramo; 3) Ángulo en B. Sol. 1) C(2, 4, -3); 2) 3 5 unidades cuadradas; 3) 143º 18’ 3’’ 2.- Cálculo vectorial 5 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 2.16) Dados los vectores v1(-2, 3. 1) y v2(-1, 3, 2) ambos aplicados en el punto P(2, 3, 2), calcular el momento del sistema respecto del punto A((-1, 0, 2) y compruébese que la suma de los dos momentos es igual al momento de la resultante respecto de A aplicada en P. Sol. 9i –9j+ 27k; 2.17) Dados los vectores deslizantes: v1(3, 2, -3) y v2(6, -3, 2) que pasan por los puntos P1(2, -6, 4) y P2(4, -1, -1), respectivamente, calcúlese: 1) La resultante del sistema de los dos vectores; 2) El momento resultante con respecto al origen; 3) El momento resultante referido al punto O’(2, -1, 5). Sol. 1) 9i – j – k; 2) 5i + 4j + 16k; 3) i – 43j + 9k 2.- Cálculo vectorial 6 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 3. CINEMÁTICA FORMULARIO Movimiento rectilíneo uniformemente var iado : 1 x = x0 + v 0 t ± a t 2 v = v0 ± a t 2 Caso particular : x0 = 0 v 0 = 0 v = 2ax Movimiento de proyectiles en el vacío : 1 x = v 0t cos α y = v0 t senα − g t 2 2 1 x2 Ecuación de la trayectoria : y = x tgα − g 2 2 v0 cos 2 α Coordenadas del vértice : x v = Velocidades : v x = v0 cos α v 02 sen 2α 2g yv = v y = v0 senα − gt v02 sen 2 α 2g v 2 = v x2 + v y2 = v 02 − 2 g y Angulo que forma la velocidad en un momento dado con la horizontal : v gt tg β = y = tgα − 2 vx v0 cos 2 α Parábola de seguridad : Alcance máximo : 3. Cinemática xM = v02 g x 2 y= − 2 g 2v02 v 02 sen 2α g 7 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 3.1) El golpe de una piedra al caer a un pozo se oye al cabo de 4,33 s. Calcular la profundidad del pozo sabiendo que la velocidad del sonido es 330 m.s-1. Sol. 82,5 m. 3.2) Un ascensor sube a la velocidad constante de 7 m/s. A la vez que arranca, desde el último piso, situado 60 metros más arriba se deja caer un grave. ¿Dónde y cuando, se encuentran ambos móviles? Sol. 20 m. 3.3) Se lanza hacia arriba un móvil con velocidad de 200 m/s. Cinco segundos después de haber lanzado éste se lanza otro móvil con igual velocidad. ¿Desde que altura sobre la horizontal de partida habrá de lanzarse este segundo móvil para que llegue al mismo tiempo que el primero al punto más alto de la trayectoria de éste? Sol. 123 m. 3.4) En un ascensor sin techo, que sube verticalmente a la velocidad constante de 2 m/s, se lanza hacia arriba una piedra a la velocidad inicial de 17,6 m/s respecto del mismo. Calcular lo que ha subido el ascensor cuando el grave cae otra vez en el mismo. Sol. 7,18 m. 3.5) Un globo se eleva verticalmente con movimiento uniforme de 90 m/min. En un instante dado se suelta una bomba que estalla al llegar al suelo. En el globo se oye la explosión 11,5 segundos después de soltarla. Hallar la altura del globo en el momento del lanzamiento. Velocidaddelsonido330m/s. Sol. 487 m. 3.6) Dividir un plano inclinado de longitud 90 metros en tres partes, que sean recorridas en tiempos iguales por un móvil que cae sin rozamiento. Sol. 10, 30 y 50 metros. 3.7) Una pelota es lanzada verticalmente hacia arriba desde el suelo, y un estudiante, desde una ventana ve que la pelota pasa hacia arriba delante de él a una velocidad de 4,9 m/s. La ventana se encuentra 9,8 m por encima del suelo. a) Qué altura alcanzará la pelota por encima del suelo. b) Cuanto tardará en ir desde la altura de 9,8 m al punto más alto. c) Calcular su velocidad y aceleración 0,5 s y 2 s después de abandonar el suelo. Sol. a) 11,02 m; b) 0,5 s; c) 9,8 m/s. 3. Cinemática 8 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 3.8) Un cuerpo que cae libremente recorre durante el último segundo de su caída la mitad del camino total. Hallar: 1) Desde que altura h cae el cuerpo y 2) Cuanto dura su caída. Sol. 1) 3,4 s; 2) 56,6 m. 3.9) Un cuerpo A es lanzado verticalmente hacia arriba con una velocidad de 20 m/s ¿A qué altura se encontraría un cuerpo B que fue lanzado horizontalmente con una velocidad igual a 4 m/s y al mismo tiempo que el cuerpo A y que luego choca con este último durante el vuelo? La distancia horizontal entre las posiciones iniciales de los cuerpos es igual a 4 metros. Encontrar también el tiempo empleado hasta el instante del choque y la velocidad de cada uno de los cuerpos en este instante. Sol. y=15,1 m; vB=10,6 m; vA=10,2 m. 3.10)Un muchacho de 1,5 metros de estatura y que está parado a una distancia de 15 metros frente a una cerca de 5 metros de altura, lanza una piedra bajo un ángulo de 45º con la horizontal. ¿Con qué velocidad mínima debe lanzar la piedra para que ésta pase por encima de la cerca? Sol. v0= 14 m/s. 3.11) Un cuerpo lanzado verticalmente hacia arriba volvió a la tierra al cabo de 3 s. 1) ¿Cual era su velocidad inicial? 2) ¿A que altura se elevó? La resistencia del aire no se toma en consideración. Sol. 1) 14,7 m/s; 2) 11 m. 3.12) Se lanza hacia arriba un móvil que tarda en llegar al punto más alto de su trayectoria 10 s. ¿A qué altura se encontrará al cabo de 5 segundos más? Sol. 367,5 m. 3.13) Un avión vuela horizontalmente a la velocidad de 734,4 km/h y a una altitud C de 4.410 metros sobre una llanura. Se suelta una bomba que estalla al chocar con el suelo. ¿Cuanto tiempo transcurre desde que se la suelta hasta que se oye el estallido en el avión? Despréciese la resistencia de aire. Sol. 46,2 s. 3. Cinemática 9 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 3.14) Un avión en vuelo horizontal, a una altura de 7.840 m y con una velocidad de 450 km. /h, deja caer una bomba al pasar por la vertical de un punto A del suelo. 1) Al cabo de cuanto tiempo se producirá la explosión de la bomba por choque con el suelo. 2) Que distancia habrá recorrido entre tanto el avión. 3) A que distancia del punto A se producirá la explosión. 4) Que tiempo tardará en oírse la explosión desde el avión, a contar desde el instante del lanzamiento de la bomba. Sol. 1) 40 s; 2) 5.000 m; 3) 5.000 m; 4) 65,6 s. 3.15) Desde la popa de un barco que avanza a 40 nudos, se lanza un proyectil de peso 100 kg con v=130 km/h y α=45º. Hallar el tiempo que tardará en alcanzar la profundidad del mar siendo esta de 500 m y a que distancia del barco se encontrará en ese momento. Densidad del proyectil, 5. Densidad del agua de mar: 1,03 g/cm3. 1 nudo = 1.852 metros/hora. Sol. t=13,7 s; d= 631,7 m. 3.16) Un proyectil lleva una velocidad inicial de 300 m/s. ¿Que inclinación habrá de darse al cañón para que alcance un blanco situado en un punto de coordenadas (x=900, y=900) sobre la horizontal de salida? Sol. 48º. 3.17) Un cañón da para el proyectil una velocidad inicial de 300 m/s y dispara bajo un ángulo de 30º, sobre un blanco situado 100 m más alto que su emplazamiento. Calcular la distancia horizontal del cañón al blanco y la velocidad con que llega a éste la bala. Sol. 178 m; 296,6 m/s. 3.18) Se lanza un proyectil bajo un ángulo de 45º en una llanura, explosionando al llegar al suelo. Se oye el ruido de la explosión 19,1 s después del disparo. Determinar la velocidad inicial del lanzamiento y la distancia al blanco. Velocidad del sonido 340 m/s. Sol. x=1.180 m; v0=108,8 m/s. 3.19) Un artillero de una pieza dispara ésta; 10 s después ve en el cielo la nubecilla de la explosión que se halla 21º 15' sobre la horizontal y 8,2 s después de verla oye el estampido que el proyectil produce al explosionar. Despreciando la resistencia del aire y suponiendo que la velocidad del sonido es 340 m/s, calcular la velocidad inicial del proyectil y el ángulo de tiro. Sol. v0=300 m/s; 30º. 3. Cinemática 10 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 3.20) Un cuerpo lanzado horizontalmente con una velocidad inicial de 100 m/s desde una cierta altura, llega al suelo con una velocidad de 110 m/s. Determinar: a) La altura desde la que se lanzó. b) El tiempo que tardó en hacer el recorrido. c) Las coordenadas del punto alcanzado al cabo del primer segundo. d) La velocidad al cabo del primer segundo. Sol. a) 107,1 m; b) 4,6 s. c) -4,9 m; d) 100,4 m/s. 3.21) Desde un lugar situado a una altura de 100 m se lanza horizontalmente un proyectil con una velocidad de 240 m/s. Dónde se encontrará el proyectil al cabo de 4 s. ¿Qué velocidad tiene en dicho momento y que ángulo forma esta velocidad con la horizontal? Sol. v=243 m/s; 9º 17'. 3.22) Desde un punto situado sobre un plano inclinado 30º sobre la horizontal, se lanza hacia la parte más alta del plano un proyectil con una velocidad inicial de 49 m/s bajo un ángulo de tiro de 45º. ¿A qué distancia cae sobre el plano inclinado? Sol. 122,5 m. 3.23) La cabina de un ascensor de altura 3 m asciende con una aceleración 2. de 1 m/s Cuando el ascensor se encuentra a una cierta altura del suelo, se desprende la lámpara del techo. Calcular el tiempo que tarda la lámpara en chocar con el suelo del ascensor. Sol. 0,745 s. 3.24) Dos ciclistas avanzan por un terreno llano. Ambos pedalean a 36 km/h. El segundo ciclista pasa por una meta volante 1 minuto después del primero. ¿Qué distancia les separa en ese instante? Unos kilómetros mas adelante, los ciclistas comienzan a subir un puerto de montaña de 18 km. El primer ciclista sube todo el puerto a 18 km/h. El segundo sube los primeros 9 km del puerto a esa misma velocidad de 18 km/h. ¿Cuánto tiempo después que el primer ciclista llega el segundo a la mitad del puerto? ¿Qué distancia les separa en esa situación? ¿A qué velocidad ha de subir el perseguidor la segunda mitad del puerto para dar alcance al escapado antes de la cima? Sol. A) 600 m; b) 1 minuto; c) 300 m; d) 18,62 km/h. 3. Cinemática 11 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 3.25) Dos ciclistas realizan una contrarreloj con 20 km de subida y 20 de llano. El ciclista A sale un minuto antes que el B. Por la cuesta ambos pedalean a 20 km/h. ¿Qué tiempo les separa cuando el segundo ciclista pasa por la mitad del puerto (km 10)?, y ¿qué distancia? ¿A qué velocidad deben pedalear por el llano para obtener una media en todo el recorrido de 30 km/h? Si ambos van a esa velocidad, ¿qué tiempo les separa cuando el primero llega a la meta? y ¿qué distancia? Sol. 1 minuto; 333 m; 60 km/h; 1 minuto; 1.000 m. 3. Cinemática 12 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 4. ESTÁTICA FORMULARIO Condiciones de equilibrio de un sólido : ΣFx = 0 ΣFy = 0 ΣFz = 0 ΣM x = 0 ΣM y = 0 ΣM z = 0 Centro de gravedad : 4. Estática x0 = Σ xi m i Σm i y0 = Σy i mi Σmi 13 z0 = Σzi mi Σmi Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 4.1) La viga de la figura, que pesa 1.000 kg. y tiene 8 m de larga, hace de carril aéreo. Sobre ella desliza un colgador en el que colocamos 2.000 kg. de carga. Calcular la tensión del cable del soporte, la fuerza ejercida por la pared sobre la viga y el ángulo que forma ésta con la horizontal cuando la carga se encuentra a una distancia de 6 m de la pared. (Se desprecian los pesos del colgador y cable). El ángulo que forma la cuerda con la pared es de 60º. Sol. T=4.000 kg; F=3.601 kg; tgα=0,29. 60º T 1.000 kp 2.000 kp 4.2) La pluma de 4 m de la grúa de la figura pesa 200 kg. y está sosteniendo una carga de 1.000 kg. Calcular la tensión de la cuerda, la fuerza sobre el perno y el ángulo que forma ésta con la horizontal. Sol. T=1.100 kg.; F=1.993; tgα=1,84. 30º 4m 200 kg 4. Estática 14 1.000 kg Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 4.3) Una puerta que pesa 60 kg está sujeta por dos goznes que están separados 1,80 m. Cada gozne soporta la mitad del peso de la puerta y su centro de gravedad se encuentra en el centro geométrico. La distancia de los, goznes a los bordes superior e inferior es la misma. La anchura de la puerta es de 1,20 m. Calcular las fuerzas que actúan sobre cada gozne y el ángulo que forman con la horizontal. Sol. H1=H2=20 kp; F1=F2=36 kp; tgα = 1,5. V2 F2 ϕ H2 O’ V1 F1 H1 1,80 m ϕ O c.m. 60 kg 1,20 m 4.4) Dos jóvenes quieren balancearse sobre un tablón de 7,2 m que está apoyado en la arista de una viga; uno de ellos pesa 48 kg y el otro 59 kg. Determinar en que punto debe apoyarse el tablón, prescindiendo de su peso, para que ambos se equilibren al sentarse en sus extremos. Si ahora se sienta un niño de 37 kg de peso precisamente en el centro entre el primer joven y el punto de apoyo en la posición anterior. ¿Cuánto habrá que correr el tablón para que continúe el equilibrio? Sol. 3,97 m; 0,51 m. 4.5) El extremo superior de una barra uniforme de 2 m de longitud y 80 kph de peso está articulado a un soporte, mientras que el inferior se halla unido a una cuerda horizontal que mantiene a la barra formando un ángulo de 40º con la vertical. Calcular la tensión T en la cuerda. Sol. 33,3 kp. 4.6) El extremo inferior de una escalera se apoya contra una pared vertical y sobre un suelo horizontal. El extremo superior está unido a la pared por medio de una cuerda horizontal de 9 m de longitud. La escalera tiene una longitud de 15 m, pesa 50 kp y su centro de gravedad se halla situado a 6 m de su extremo inferior. Calcular la tensión de la cuerda cuando un hombre de 75 kp de peso se encuentra a una distancia de 3 m del extremo superior. Sol. T=60 kp. 4. Estática 15 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 4.7) Hallar la resultante de las cuatro fuerzas indicadas en el siguiente diagrama. Sol. R=832 kp; x=2,28 m. 150 kp 400 kp 30º 30º R 1,5 m O 100 kp 250 kp 30º 2,5 m 1m x x 4.8) El eje AB de la grúa, cuyo peso es G = 15 kN gira en la quicionera B y en el cojinete A. La grúa tiene colgado en el punto C un peso Q = 8 kN. Determinar las reacciones de la quicionera y del cojinete sí la distancia AB = 4 m, la distancia entre el centro de gravedad de la grúa y el eje de su rotación KD = 1 m y la distancia entre el punto C y el mismo eje EC = 2 m. Sol. y B=23 kN; xA=xB=7,75 kN. A 2m C K 1m Q 4m G B 4.9) Una viga AB de longitud l=6m y peso P=800 kg está fija en A y forma con la horizontal un ángulo α=60º gracias al cable BC, que une el extremo B de la viga con el punto C del suelo que dista de A, AC=S=4 metros. Calcular la tensión en el cable, la reacción en A y el ángulo que forma esta última con la horizontal. Sol. T=500 kp; F= 1.170 kp; γ=70º. B 60º A C 4. Estática 16 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 4.10) Una escalera de 10 m de longitud tiene una masa de 20 kg. Descansa sobre una pared vertical lisa, y su parte inferior se encuentra en el piso a 3 m de la pared. ¿Cuál debe ser el coeficiente mínimo de fricción estática entre escalera y suelo para que una persona de 70 kg pueda subir con seguridad hasta el 80% de la escalera? Sol. µ = 0,40 4.11) El puntal de la figura pesa 40 kg y su centro de gravedad está en su punto medio. Calcular: a) La tensión del cable; b) Las componentes horizontal y vertical de la fuerza ejercida sobre el puntal por la pared. Sol. a) 133 kg; b) H=106 kg, V=20,2 kg. 1,80 m 3m 2,4 m 40 kg α 60 kg 4.12) Una barra de hierro de 2 m de largo que pesa 50 kg puede girar alrededor de uno de sus extremos, del otro extremo pende un peso de 10 kg y queremos mantener la barra en posición horizontal mediante una cuerda que pasa por una polea con uno de sus extremos unido a la barra formando con ésta un ángulo de 30º. ¿Qué número de kg debemos colocar en el otro extremo para que el sistema esté en equilibrio, y cual son las reacciones sobre O? Sol. T=70 kg, H=60 kg, V=25 kg. 30º 10 kg 50 kg 4. Estática 17 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 4.13) Una carga que pesa 300 kp se eleva desde el suelo, como indica la figura, y cuelga 20 metros por debajo de la polea. a) ¿Qué fuerza horizontal se necesita para desviarla horizontalmente 50 cm hacia el edificio? b) ¿Qué fuerza para acercarla horizontalmente 6 m? c) ¿Cuál será entonces la tensión de la cuerda que soporta el peso? Se mantiene constante la longitud de la cuerda. Sol. a) 7,503 kg; b) 94,350 kg; c) 314,487 kg 20 m 300 kg. 4.14) Una puerta de 2,40 m de larga y 1,20 m de alta pesa 40 kg. Su centro de gravedad se encuentra en su centro, y está suspendida en A y B. Para aliviar el esfuerzo sobre el gozne superior se dispone un cable CD como indica la figura. Se aumenta la tensión en CD hasta que la fuerza horizontal sobre el gozne A sea nula. a) ¿Cuál es la tensión en el cable CD? b) Cuál es el valor de la componente horizontal de la fuerza en el gozne B? c) ¿Cual es la fuerza vertical ejercida en conjunto por los goznes A y B? Sol. a) 21,4 kg; b) 18,61 kg; c) 29,3 kg. D 30º C A 1,2 m B 4,2 m 40 kg 4. Estática 18 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 4.15) Una puerta de garaje está montada sobre un carril aéreo, como indica la figura. Las ruedas A y B están oxidadas, de modo que no ruedan, sino que deslizan sobre el carril. El coeficiente cinético de rozamiento es 0,5. La distancia entre las ruedas es 2 m y cada una dista 0,5 m de los bordes verticales de la puerta. La puerta es simétrica, pesa 800 N y es empujada hacia la izquierda a velocidad constante por una fuerza horizontal P. a) Sí la distancia h es 1,5 m, ¿Cual es la componente vertical de la fuerza ejercida sobre cada rueda por el carril? b) Calcúlese el valor máximo que puede alcanzar h sin que ninguna rueda se desplace ni separe del carril. Sol. a) 700 N, 100 N; b) 2 m. 2m A B h P 4.16) Una varilla homogénea de 20 kg de peso se apoya como indica la figura. Determínese: a) Diagrama de fuerzas. b) Fuerza horizontal, F, que se debe aplicar al extremo M de la varilla para que se mantenga en equilibrio con un ángulo de inclinación con la horizontal de 30º. Se supone que el ángulo de la pared en que se apoya el otro extremo de la varilla, N, con la horizontal es de 60º y además que no existen rozamientos. N F 30º M 4. Estática 19 60º Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 4.17) Un extremo de una barra de 1 m está como muestra la figura. El otro extremo está sujeto con una cuerda ligera que forma un ángulo ϕ con la barra. El coeficiente estático de rozamiento es 0,30. a) ¿Cuál es el valor máximo que puede tener el ángulo ϕ para que la barra permanezca en equilibrio? b) Sea el valor de ϕ igual a 10º. UN cuerpo del mismo peso que la barra se suspende de ésta, como se representa, a una distancia x de la pared. ¿Cuál es el valor mínimo de x para que la barra siga en equilibrio? c) Cuando ϕ = 10º ¿Qué valor ha de tener el coeficiente estático de rozamiento para que pueda sujetarse el cuerpo del extremo izquierdo de la barra sin que éste deslice? Sol. a) 16,7º; b) 0,24 m; c) 0,53. F ϕ 1m x 4.18) Uno de los extremos de una regla de longitud L = 1 m, está sostenido por un hilo inextensible y sin peso, fijo a una pared vertical. El otro extremo de la regla en posición horizontal. El hilo y la regla forman ángulo α y el coeficiente de rozamiento estático entre la pared y la regla es µ = 0,3. a) Máximo valor de α para que la regla se mantenga en equilibrio. b) Siendo α = 10º, se suspende un objeto pesado de la regla a una distancia “x” de la pared. El peso de este objeto es igual al de la regla. Se pide el valor mínimo de “x” para que el sistema se mantenga en equilibrio. Sol. a) 16,7º; b) 0,24 m. 4. Estática 20 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 4.19) Calcular el centro de gravedad de la siguiente figura. Sol. x0=9/4 cm, y 0=17/8 cm. 2 cm 5 cm 3 cm 4 cm 4.20) Calcular la posición del centro de gravedad de la superficie plana representada en la figura. Sol. x0 = 6,28 cm, y 0 = 3,57 cm. 4 cm 8 cm 2 cm 10 cm 4.21) Determinar la posición del centro de gravedad de un disco del cual han sido cortados dos pedazos circulares como se indica en la figura. Los radios de los huecos son iguales a la mitad y a la cuarta parte del radio R del disco, respectivamente. Sol. 3R/22. R 2 R /4 R 2 πR µ 4. Estática 21 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 4.22) Un peso P se encuentra sujeto por dos cuerdas tal como muestra la figura. Calcular: a) Las tensiones TA y TB , sí el peso P es de 3.000 N. b) Las tensiones máximas que pueden soportar las cuerdas son de 5.000 N. ¿Cuál será el máximo valor de P que pueden soportar estas cuerdas sin romperse? c) Cuando P vale 3.000 N, si se rompe la cuerda del nudo B, qué velocidad adquirirá el peso P al pasar por la vertical de A. A 2m 30º B P 4.23) Una masa de 360 kg pende de un cable sujeto a una barra de acero de 15 m de longitud que pivota en una pared vertical y se soporta mediante un cable como indica la figura. La masa de la barra es de 85 kg. a) Con el cable sujeto a la barra a 5,0 m del extremo inferior, como se indica, determinar la tensión del cable y la fuerza ejercida por la pared sobre la barra de acero. b) Repetir el cálculo con un cable algo más largo sujeto a la barra de acero en un punto a 5,0 m de su extremo superior, manteniendo el mismo ángulo entre la barra y la pared. Sol. a) T=10.265 N, H=5.132 N, V=4.523 N; b) T=5.923 N, H=5.129 N, V=1.404 N 60º 15 m 10 m 360 kg 5m 4. Estática 22 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 4.24) Sobre la armadura de un puente actúan fuerzas verticales P1= 20 kN y P2=40 kN a distancias de 10 y 40 metros respectivamente del extremo izquierdo de la armadura, y una fuerza horizontal P3= 30 kN a nivel de la armadura superior de la celosía CD: La altura de la celosía AC es de 6 m. Hallar la resultante de las fuerzas P1, P2 y P3. Sol.x=29,55 m, x’=26,87 m, α=63º 25’ P3 C A P1 R 10 m 30 m P2 10 m 4.25) Un tronco uniforme de masa 100 kg, longitud 4 m y radio 12 cm se mantiene en posición inclinada como indica la figura. El coeficiente de rozamiento estático entre el tronco y la superficie horizontal es 0,6. El tronco está a punto de deslizar hacia la derecha. Determinar la tensión en el alambre soporte y ángulo que el alambre forma con la pared vertical. Sol. 636 N; 21,48º θ 4m r=12 cm 20º 4. Estática 23 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 4.26) La figura muestra una escalera de 20 kg apoyada contra una pared sin rozamiento y descansando sobre una superficie horizontal también sin rozamiento. Para evitar que la escalera deslice, la parte inferior de la escalera se ata a la pared con un alambre delgado; la tensión del alambre es de 29,4 N. El alambre se romperá si la tensión supera los 200 N. a) Si una persona de 80 kg asciende hasta la mitad de la escalera, ¿qué fuerza ejercerá ésta sobre la pared? b) ¿Hasta qué altura puede ascender una persona de 80 kg con esta escalera? 20 kg 5m 1,5 m 4.27) Una viga homogénea AB de 6 m de longitud y masa 500 kg se encuentra en equilibrio como indica la figura. Dibujar todas las fuerzas que actúan sobre la viga. Calcular la masa MX para que la viga permanezca en equilibrio y la reacción en A (modulo y dirección). Sol. R = 6482 N; 71o con la horizontal, Mx = 500 kg 30º B Mx 30º µ=0 60º A 4.28) Dos personas, A y B, transportan a velocidad constante y en equilibrio un tablón de 10 kg y 4 m de longitud, cada uno por un extremo. Sobre el tablón se apoya una caja de 60 kg, a 1,5 m de B. Hallar la fuerza que soporta cada persona. Sol. FA = 269,5 N; FB = 417 N. 4. Estática 24 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 4.29) Una barra de acero homogénea de 200 kg y 10 m de longitud se cuelga por su centro del punto A (ver figura) mediante un cable de masa despreciable. Un extremo de la barra se apoya sin rozamiento sobre la pared. Cuando en el otro extremo se cuelga una masa m, la barra forma un ángulo de 60o con la vertical y 90o con el cable que la sostiene. Dibujar todas las fuerzas que actúan sobre la barra. Calcular el valor de m, la tensión de los dos cables y la fuerza ejercida por la pared sobre la barra. Sol. T1= 3394,8 N; T2= 980 N; m = 100 kg; N = 1697,4 N. A 600 m 4.30) Una persona de masa 70 kg se sienta en el extremo de una viga homogénea de 4 m de longitud y masa 1000 kg. La viga esta sujeta a la pared por un cable y el sistema permanece en equilibrio estático en la posición que muestra la figura. Dibujar todas las fuerzas que actúan sobre la viga. Calcular la tensión del cable y la reacción ejercida por la pared sobre la viga. Sol. T = 1.612g kg; H = 1.140g N; V = 70g N. 2m 2m 4m 4. Estática 25 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 4.31) La figura muestra una viga uniforme de 20 cm de longitud descansando sobre un cilindro de 4 cm de radio. La masa de la viga es de 5,0 kg y la del cilindro 8,0 kg. El coeficiente de rozamiento entre la viga y el cilindro es cero. a) Determinar las fuerzas que actúan sobre la viga y sobre el cilindro. b) ¿Cuáles deben ser los coeficientes mínimos de rozamiento estático entre la viga y el suelo y entre el cilindro y el suelo para evitar el deslizamiento? Sol. a) N1 = 28,3 N, N2 = 24,5 N, FN = 103,1 N; b) µv-s = 0,58, µc-s = 0,14 30º 4. Estática 26 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 5. DINÁMICA FORMULARIO Movimiento lineal Momento lineal : p = Σmi v i = M v Ecuación fundamental de la dinámica : Pr incipio de D' Alambert : F = ma ΣFi − m a = 0 Movimiento curvilíneo Fuerza centrífuga y centrípeta : 5. Dinámica Fc = m a n = m 27 4π 2 v2 = mω 2 r = m 2 = m 4 π 2 v 2 r r T Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 5.1) Una grúa de puente, cuyo peso es P = 2x104 N, tiene un tramo de L = 26 m. El cable, al que se cuelga la carga se encuentra a una distancia l = 10 m de uno de los rieles. Determinar las fuerzas de presión de la grúa sobre los rieles, al levantar una carga de P0=104 N de peso con una aceleración a = 9,8 m/s2. Sol. 2,23x104 N; 1,77x104 N. L l 5.2) A través de una polea que permanece inmóvil, pasa una cuerda de la cual están suspendidas tres cargas iguales, cada una de 2 kg de masa. Encontrar la aceleración del sistema y la tensión de la cuerda que une a los bloques 1 y 2. Sol. 3,3 m/2; 13 N. 2 1 3 5.3) Calcular la aceleración de las cargas y las tensiones de las cuerdas en la siguiente figura. Se desprecia la fricción con el plano. Sol. 3,5 m/s2; 50,4 N; 33,6 N. T2 T1 2kp 4 kp 30º 5. Dinámica 28 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 5.4) En el sistema de cargas representado en la figura P1= 1 kgf; P2= 2 kgf; P3= 5 kgf; P4= 0,5 kgf; α = 30º. El coeficiente de rozamiento de las cargas con el plano es igual a 0,2. Encontrar la aceleración del sistema de cargas, las tensiones de las cuerdas y la fuerza con la cual el bloque P4 hace presión sobre P3. Sol. 6,9 m/s2; 16 N; 8,6 N. P1 P2 30º P3 5.5) Un cuerpo de 1.500 kp de peso que pende del extremo de un cable, desciende con una velocidad de 4 m/s. Sabiendo que el espacio que recorre hasta detenerse es de 3 m, calcular la tensión en el cable suponiendo que la deceleración es constante. Sol. 1.908 kp. 5.6) De los extremos de una cuerda, que pasa por una polea sin rozamiento, penden dos cargas de 2 y 6 kp de peso. Calcular la aceleración y la tensión de la cuerda. Sol. 4,9 m/2; 3 kp. 5.7) Un bloque de 100 kp de peso se mueve a lo largo de una superficie rugosa horizontal por la acción de una fuerza de 50 kp, que forma un ángulo de 30º con la horizontal. Sabiendo que el coeficiente de rozamiento es 0,2. Calcular el espacio recorrido por el bloque a los 10 s de iniciarse el movimiento. Sol. 139 m. 5. Dinámica 29 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 5.9) Un hombre tira de dos trineos enlazados entre sí por medio de una cuerda que forma un ángulo de 45º con la horizontal y a la cual aplica una fuerza de 12 kp. Las masas de los trineos son iguales a m1= m2= 15 kg. El coeficiente de rozamiento de los patines con la nieve es igual a 0,02. Encontrar: 1) la aceleración de los trineos y la tensión de la cuerda que los mantiene unidos; 2) la fuerza con que el hombre debe tirar de la cuerda para que los trineos se muevan uniformemente. Sol. 1) 2,6 m/s2, 42 N; 2) 8,2 N. 12 kp 15 kg 15 kg 45º 5.10) Un patinador, que pesa 70 kgf está parado en el hielo (con los patines puestos) y tira una piedra, que pesa 3 kgf, en dirección horizontal con una velocidad de 8 m/s. Hallar hasta que distancia retrocederá el patinador al lanzar la piedra, sabiendo que el coeficiente de rozamiento entre los patines y el hielo es igual a 0,02. Sol. 0,29 m. 5.11) Dos bloques que pesan 8 y 16 kg, respectivamente, están unidos por una cuerda y deslizan hacia abajo sobre un plano inclinado 30º, como indica la figura. El coeficiente cinético de rozamiento entre el bloque de 8 kg y el plano es 0,25, y entre el bloque de 16 kg y el plano es 0,50. a) Calcular la aceleración de cada bloque, b) Calcular la tensión de la cuerda. Sol. 1,35 m/s2; b) 1,16 kg. 16 kg 30º 5. Dinámica 8 kg 30 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 5.12) El bloque de la figura tiene una masa de 4 kg y m2 tiene una masa de 2 kg. El coeficiente de fricción entre m2 y el plano horizontal es 0,5. El plano inclinado carece de rozamiento. Determinar: a) la tensión de la cuerda y b) la aceleración de los dos bloques. Sol. a) 1,6 m/s2; b) 13 N. m1 30º 5.13) Un tren toma una curva de 150 m de radio a una velocidad de 50 km/h. Hallar la pendiente que debe tener el peralte para que se ejerza la misma fuerza sobre cada carril. Sol. 7,5º. 5.14) Una piedra lanzada sobre una superficie de hielo con la velocidad v = 2 m/s recorrió hasta detenerse por completo, la distancia s = 20,4 m. Hallar el coeficiente de rozamiento entre la piedra y el hielo, considerando que es constante. Sol. 0,01. 5.15) El cuerpo de peso G bajo la acción de la fuerza de la gravedad baja por el plano inclinado que forma con el horizonte el ángulo α = 30º. Determinar la velocidad del cuerpo, transcurridos 2 segundos desde el inicio del movimiento, y el camino recorrido para este tiempo, si el coeficiente de rozamiento es 0,3. Sol. 4,8 m. 5.16) Un cuerpo de 5 kg de masa, se mueve sobre un plano horizontal por la acción de una fuerza de 3 kp, que se aplica al cuerpo formando un ángulo de 30º con la horizontal. El coeficiente de rozamiento es igual a 0,2. Calcular la velocidad del cuerpo después de 10 segundos de haber sido aplicada la fuerza y el trabajo de la fuerza de fricción durante este tiempo. Sol. 37 m/s; 1.276 J. 5.17) En el extremo superior de un plano inclinado 30º sobre la horizontal, hay una polea por cuya garganta pasa un cordón. Uno de los extremos del cordón sostiene un peso de 10 kg, el otro extremo mantiene paralelo al plano inclinado un cuerpo que pesa 10 kg; el coeficiente de rozamiento entre el cuerpo y el plano es 0,5. Calcular: 1) La aceleración del sistema. 2) La tensión de la cuerda. Sol. 1) 0,367 m/s2; 2) 9,625 kp 5. Dinámica 31 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 5.18) En un "tiovivo" hay una cadena de la que pende un asiento que, por la fuerza centrífuga ocasionada por el giro, se aparta de la vertical. Del punto de sujeción al eje hay 3 metros; la cadena tiene una longitud de 3 metros y su masa es despreciable comparada con la que existe en el extremo y se supone inextensible y completamente flexible. La cadena forma un ángulo de 30º con la vertical. ¿Cuantas vueltas da por minuto el "tiovivo”? Sol. 10,20 r.p.m. 5.19) Un cuerpo se desliza primeramente por un plano inclinado que forma con el horizonte un ángulo de 8º y después por una superficie horizontal. Hallar a que será igual el coeficiente de rozamiento si la distancia que el cuerpo recorre por la superficie horizontal igual a la que recorre por el plano inclinado. Sol. 0,07 5.20) Queremos elevar un cuerpo que pesa 300 kg con una aceleración de 5 2 m/seg mediante un cable colocado verticalmente. Calcular la tensión a que está sometido el cable. Sol. 453 kg. 5.21) Sobre un plano inclinado 30º se desliza una masa m1, por una polea unida a una masa m al otro extremo. La masa m se eleva 245,25 m en 20 s, si se invierten las masas ¿en qué sentido se efectuará el movimiento y cuál será el espacio recorrido en 20 s? 1º) Sin rozamiento, 2º) Con rozamiento k=0,2 Sol. 1.220 m; 1.560 m. m1 m2 30º 5.22) Un bloque de hierro de 7 kg de peso es arrastrado sobre una mesa horizontal de madera, por la acción de un peso de kg que cuelga verticalmente de una cuerda horizontal unida al bloque de hierro y que pasa por una polea ligera. El coeficiente de rozamiento entre el hierro y la mesa es 0,15. Hallar la aceleración del bloque y la tensión de la cuerda. Sol. 1 m/s2; 1,76 N. 7 kp 2 kp 5. Dinámica 32 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 5.23) Un bloque pende del extremo de una cuerda. Calcular la masa de dicho bloque sabiendo que la tensión de la cuerda es a) 4,9 N; b) 1 Kp; c) 4,9x105 dinas. 5.24) Calcular el espacio que recorrerá un cuerpo de 5 kg de masa, cuando sobre él actúa una fuerza constante de 1 N durante 10 seg. Sol. 10 m 5.25) Calcular la fuerza constante de rozamiento necesaria para detener en 5 segundos un automóvil de 1.500 Kp de peso que marcha a una velocidad de 90 Km/h ¿qué espacio recorrerá hasta detenerse? Sol. 765 kp; 62,5 m. 5.26) Calcular la aceleración y el tiempo que tarda en recorrer 70 m un cuerpo de 12 kp de peso sometido a la acción de una fuerza constante de 3 Kp. Sol. 2,46 m/s2; 7,54 s. 5.27) Un cuerpo de 100 Kp de peso pende del extremo de una cuerda. Calcular su aceleración cuando la tensión en la cuerda es a) 125 Kp; b) 80 Kp; c) 100 Kp. Sol. 2,55; 2,04; 0 m/seg2. 5.28) El ascensor de una mina, que pesa 800 Kp, arranca hacia arriba con una aceleración de 6 m/seg2. Calcular la tensión en el cable en el momento del arranque. Sol. 1.290 Kp. 5.29) ¿Qué fuerza hacia arriba se debe aplicar a un cuerpo de 50 Kp de peso para que su aceleración de caída sea 3 m/seg2? Sol. 34,7 Kp. 5.30) El peso de un ascensor es de 1.200 Kp. Calcular la tensión en los cables cuando a) asciende con una aceleración de 1m/seg2, b) desciende con una aceleración de 1m/seg2. Sol. 1.322 Kp; 1.078 Kp. 5.31) Un paracaidista de 70 kp de peso se lanza libremente al espacio desde el reposo y a los 5 segundos del instante del lanzamiento abre el paracaídas. Este tarda en abrirse por completo 0,8 segundos y la velocidad pasa a 12 m/seg. cuando está totalmente abierto. Calcular la fuerza media ejercida sobre las cuerdas del paracaídas, suponiendo que éste carece de peso. Sol. 400 Kp 5. Dinámica 33 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 5.32) Un vagón de 1.000 kp de peso es arrastrado sobre una vía horizontal por un caballo de 500 kp. Sabiendo que la fuerza de rozamiento sobre el vagón es de 150 kp, calcular: a) la fuerza que debe ejercer el caballo para que el vagón adquiera una velocidad de 10 m/s a los 5 segundos de iniciado el movimiento; b) la máxima tensión que debe soportar la cuerda. Sol. a) 456 kp; b) 354 kp. 5.33) Un bloque de masa m = 5 kg desliza por una superficie inclinada 37º con la horizontal, como se indica en la figura. El coeficiente cinético de rozamiento es de 0,25. Se enrolla una cuerda unida al bloque alrededor de un volante cuyo eje fijo pasa por O. El volante es un cilindro de masa M = 20 kg y radio exterior R = 0,2 m. a) ¿Con qué aceleración desliza el bloque por el plano? b) ¿Cuál es la tensión de la cuerda? Sol. a) 1,97 s/m-2; b) 9,85 N. O m = 5 kg 37º 5.34) Dos bloques, A y B, están dispuestos como indica la figura, y unidos por cuerdas al bloque C. Tanto A como B pesan 20 N y el coeficiente cinético de rozamiento entre cada bloque y la superficie es 0,5. El bloque C desciende a velocidad constante. Calcular: a) La tensión de la cuerda que une los bloques A y B. b) El peso del bloque C. Sol. a) T = 10 N; b) F = 10 N. B A 20 N 20 N 5. Dinámica F 34 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 5.35) Un bloque de 0,05 kg de masa está unido a una cuerda que pasa a través de un orificio practicado en una superficie horizontal sin rozamiento, como indica la figura. El bloque está girando inicialmente, a una distancia de 0,2 m del orificio, con una velocidad angular de 3 rad/s, Se tira entonces de la cuerda hacia abajo, acortando el radio del círculo descrito por el bloque a 0,1 m. El bloque puede considerarse como una masa puntual. a) ¿Cuál es la nueva velocidad angular? b) Hállese la variación de energía cinética del bloque. Sol. a) 12 rad/s; b) 0,027 J. F 5.36) a) Si se necesitan 20 C.V. para mover un automóvil de 1.200 kg de masa a 50 km/h sobre una carretera horizontal, ¿cuál es la fuerza total retardadora debida al rozamiento, al viento, etc.? b) ¿Qué potencia se necesita para mover el automóvil a 50 km/h por una pendiente del 10 % (es decir que sube 10 m en vertical en 100 m horizontales) c) ¿Qué potencia se necesita para hacerlo descender a 50 km/h por una pendiente del 2 %? d) ¿Cuál sería la pendiente, en tanto por ciento, para que el automóvil descendiera con el motor apagado a 50 km/h? Sol. a) 1.073 N; b) 41,9 C.V.; c) 15,6 C.V. d) 9,1 %. 5. Dinámica 35 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 5.37) Se ejerce una fuerza de 12 N en dirección horizontal contra un bloque A, de 4 kg, el cual empuja, a su vez, a otro bloque B, de 2 kg, conforme indica la figura. Calcular la aceleración del sistema y la fuerza que ejerce cada bloque sobre el otro: a) Si ambos bloques se encuentran sobre una superficie lisa. b) Si los coeficientes de rozamiento dinámicos entre los bloques A y B y la superficie son, respectivamente, 0,1 y 0,2. Sol. a) 4 N; b) 0,69 m/s2, 5,3 N. A F B 5.38) Un bloque de 4 kg cuelga de una cuerda ligera que a través de una polea sin rozamiento está conectada a un bloque de 6 kg que descansa sobre una plataforma rugosa. El coeficiente de rozamiento cinético µ = 0,2. El bloque de 6 kg se empuja contra un muelle, al cual no está sujeto. El muelle tiene una constante de fuerza de 189 N/m y se comprime 30 cm. Determinar la velocidad de los bloques cuando el muelle se libera y el bloque de 4 kg cae una distancia de 40 cm. Sol. 0,7024 m; 4,92 N m1=6 kg m2=4 kg 5. Dinámica 36 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 5.39) Un bloque comienza a desplazarse con una velocidad de 7 m/s, sobre una superficie horizontal rugosa. El coeficiente de rozamiento entre el bloque y la superficie es 0,3. Después de recorrer una distancia de 2 m, encuentra una rampa inclinada 40º respecto a la horizontal y con el mismo coeficiente de rozamiento anterior. Hallar: a) la velocidad del bloque cuando alcanza la base de la rampa b) la distancia que recorrerá sobre la rampa, antes de quedar momentáneamente en reposo. Sol. a) 6,08 m/s; b) 2,12 m. 5.40) Sea el sistema de la figura. El coeficiente de rozamiento entre el suelo y el cuerpo A es 0,4 y entre el suelo y B es 0,1. Las masas de los cuerpos son: mA = 10 kg, mB = 30 kg, mc = 15 kg; a) calcular las tensiones en las cuerdas y la aceleración de cada cuerpo; b) ¿qué peso hay que quitar al bloque C para que baje con velocidad constante?, c) ¿y para que suba con velocidad constante? Sol. a) T1 = 108,2 N, T2 = 156,5 N; b) 3,54 kg hay que quitar a C; c) no es posible este movimiento quitando peso a C. B A 10 kg 30º 5. Dinámica 30 kg C 37 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 5.41) Un cuerpo de masa 20 kg parte del extremo O de una mesa con velocidad inicial v0 = 3i m/s. Sobre el actúa en todo momento (incluso en el aire) una fuerza constante F = 19,6i N. El coeficiente de rozamiento mesa-cuerpo es µ = 0,1. Hallar el punto en el que el cuerpo choca con el suelo. Dibujar x(t) e y(t) desde que el cuerpo sale de O hasta que choca con el suelo. Sol.9,49 m de la primera pata. F A O H = 4,9 m d=6m 5. Dinámica 38 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 6. TRABAJO FORMULARIO Trabajo : dW = F dr cos ϕ Energía cinética : W = 1 m v2 2 P= Potencia : dW = F .v dt Energía potencial : U = mgh Trabajo realizado por un par al hacer girar a un cuerpo alrededor de un eje : Energía cinética de un cuerpo en rotación alrededor de un eje : 6. Trabajo 39 W = 1 I ω2 2 W =Mϕ Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 6.1) Un cuerpo de 3 kg de masa cae desde cierta altura con una velocidad inicial de 2 m/s dirigida verticalmente hacia abajo. Calcular el trabajo realizado durante 10 segundos contra las fuerzas de rozamiento, si se sabe que al final de este intervalo de tiempo el cuerpo adquiere una velocidad igual a 50 m/s. La fuerza de resistencia se considera constante. Sol. 3.900 Julios. 6.2) ¿Que trabajo hay que realizar para que un cuerpo en movimiento de masa igual a 2 kg: 1) Aumente su velocidad desde 2 m/s hasta 5 m/s? 2) Se pare cuando su velocidad inicial sea 8 m/s. Sol. 1) 21 J; 2) 64 J. 6.3) Una piedra está atada a una cuerda de longitud l = 50 cm y gira uniformemente en un plano vertical. Hallar a que número de revoluciones por segundo se romperá la cuerda sabiendo que su carga de rotura es igual a 10 veces el peso de la piedra. Sol. 2,1 r.p.s. 6.4) Hallar que potencia desarrollará el motor de un automóvil de 1.000 kg de masa, sabiendo que marcha a la velocidad constante de 36 km./h: 1) por una carretera horizontal; 2) subiendo una cuesta cuya pendiente es de 5 m por cada 100 m de recorrido y 3) bajando una cuesta con esta misma pendiente. El coeficiente de rozamiento es igual a 0,07. Sol. 1) 6,9 kw; 2) 11,7 kw; 3) 1,9 kw. 6.5) Un cuerpo desliza primero a lo largo de un plano inclinado un ángulo de 30º y luego continúa moviéndose sobre el plano horizontal. Determinar el coeficiente de rozamiento, si se sabe que el cuerpo recorre en el plano horizontal la misma distancia que en el plano inclinado. Sol. 0,27. 6.6) Una piedra ha sido lanzada formando un ángulo α = 60º con el horizonte a la velocidad v0= 15 m/s. Hallar las energías cinética, potencial y total de la piedra: 1) un segundo después de haber sido lanzada; 2) en el punto más alto de su trayectoria. La piedra tiene una masa m = 0,2 kg. Sol. 1) 15,9 J; 2) 22,5 J. 6. Trabajo 40 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 6.7) Un cuerpo que pesa P1= 2 kgf se mueve al encuentro de otro cuyo peso P2= 1,5 kgf y choca quedando ambos unidos después del choque. Las velocidades de los cuerpos inmediatamente antes del choque eran respectivamente iguales a v1= 1 m/s y v2= 2 m/s. ¿Cuánto tiempo durará el movimiento de estos cuerpos después del choque sí el coeficiente de rozamiento es 0,05? Sol. 0,58 s. 6.8) Una grúa de 250 C.V. de potencia tiene un rendimiento de 0,75 y eleva un peso de 25 toneladas a 10 metros de altura. La energía cuesta 13 pesetas el kilovatio-hora. Calcular el tiempo que invierte en levantar el peso y su importe. Sol. 17,7 s; 11,70 ptas. 6.9) Un objeto se deja caer por un carril desde una altura h de modo que, al llegar a la parte más baja, debe describir el “rizo de la muerte”, tal como se indica en la figura. El radio de la circunferencia es R = 3 m. Hallar la altura h mínima desde la que debe dejarse caer el objeto, despreciando los rozamientos. Sol. 7,5 m. m R h’ h 6.10) Un automóvil cuya masa es de 2 Tm sube por una cuesta. La inclinación de esta cuesta es igual a 4 m por cada 100 m de recorrido. El coeficiente de rozamiento es igual a 0,08. Hallar: 1) el trabajo que realiza el motor del automóvil en recorrer 3 km y 2) la potencia que desarrolla el motor, sabiendo que este camino fue recorrido en 4 minutos. Sol. 1) 7x106 J; 29,4 kw. 6.11) Un ciclista viaja cuesta abajo por una pendiente de 6º con una velocidad uniforme de 7 km/h. Suponiendo que tiene una masa total de 75 kg (el ciclista más la bicicleta) ¿Cuál debe ser la potencia del ciclista para subir la misma pendiente con la misma velocidad? Sol. 299 w. 6. Trabajo 41 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 6.12) Un coche de juguete de masa total M = 1 kg, está construido con cuatro ruedas macizas de 10 g. El coche se deja en libertad en un plano inclinado de pendiente del 5%, y recorre 150 cm en 2,5 segundos. Encontrar el valor de "g" en el lugar de la experiencia. Las ruedas no deslizan. Sol. 978 cm.s-2. 6.13) Se tiene un carrete, como se muestra en la figura, que rueda sobre un plano inclinado de ángulo de elevación α = 30º. Parte del reposo en A y llega a B, en desnivel h. Calcular el tiempo que tarda en pasar desde A a B. Datos: m1 = m2 = m3 = 1 kg; h = 1 m; a = 01 m; b = 0,12 m Sol. t = 1,08 s. m1 m3 2b A 2a m2 h α B 6.14) Un bloque de 2 kg se deja libre sobre un plano inclinado hacia abajo, sin rozamiento, a una distancia de 4 m de un muelle de constante k = 100 N/m. El muelle está fijo a lo largo del plano inclinado que forma un ángulo de 30º. a) Hallar la compresión máxima del muelle, admitiendo que carece de masa. b) Si el plano inclinado no es liso sino que el coeficiente de rozamiento es 0,2, hallar la compresión máxima. c) En el caso último del plano inclinado rugoso, ¿hasta qué punto subirá el bloque por el plano después de abandonar el muelle? Sol. a) 0,989 m; b) 0,783 m; c) 1,54 m. 2 kg 4m k =100 N/m 30º 6. Trabajo 42 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 6.15) Un coche de 1.500 kg de masa que se desplaza con una velocidad de 24 m/s se encuentra al pie de una colina de 2 km de longitud y cuya altitud es de 320 m. En la cima de la colina la velocidad del coche es de 10 m/s. Suponiendo que el coeficiente de rozamiento dinámico es 0,1, calcular la potencia media desarrollada por el motor del coche. Sol. 68 kw 6.16) Un móvil de masa 2 kg cae desde el punto P0 sin velocidad inicial. El coeficiente de rozamiento entre el plano inclinado y el cuerpo es320 µ =m0,1 A) ¿tiene el cuerpo la misma energía en P1 que en P0? ¿dónde ha ido a parar la energía perdida? B) Hallar la velocidad del cuerpo en el punto P1. C) A partir del punto P1 el cuerpo desliza sin rozamiento por una pista de hielo horizontal hasta que choca con el cuerpo de masa 5 kg. Si ambos cuerpos quedan unidos tras el choque (choque plástico) hallar su velocidad. Sol. A) No porque se pierde en rozamiento; B) v = 9 m/s; C) vF = 2,6 m/s 6.17) Una esfera maciza de radio R, se deja caer por un carril desde una altura h de modo, que al llegar a la parte más baja, debe describir el “rizo de la muerte”, tal como se indica en la figura. El radio de la circunferencia es r = 5 metros. Hallar la altura h mínima desde la que debe dejarse caer la esfera. Despréciese los rozamientos. Momento de inercia de la esfera maciza 2/5 MR2. Sol. 13,5 m m R h’ h 6. Trabajo 43 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 7. DINÁMICA DE ROTACIÓN 7.1) Un niño hace que ruede un aro por un camino horizontal con la velocidad de 7,2 km./h. ¿Hasta que distancia podría subir el aro por una cuesta a costa de su energía cinética? La inclinación de la cuesta es igual a 10 m por cada 100 m de camino. Sol. 4 m. 7.2) En un tambor de masa M = 9 kg hay enrollado un cordón a cuyo extremo va atado un peso de masa m = 2 kg. Hallar la aceleración del peso. Considerar que el tambor es un cilindro homogéneo y despreciar el rozamiento. Sol. 3 m/s2. 7.3) Un ventilador gira con una velocidad correspondiente a 900 r.p.m. Este ventilador, al ser desconectado, empieza a girar con movimiento uniformemente retardado y da 75 vueltas hasta que se para por completo. El trabajo de las fuerzas que lo frenan es igual a 44,4 J. Hallar: 1) el momento de inercia del ventilador y 2) el momento de las fuerzas que lo frenan. Sol. 1) 0,01 kg.m2; 2) 0,094 N.m. 7.4) Un volante cuyo momento de inercia I = 245 kg.m2 giraba a 20 r.p.s. Después que el momento de rotación de las fuerzas dejó de actuar sobre el volante, éste dio 1.000 vueltas y se paró. Hallar: 1º) el momento de las fuerzas de rozamiento, 2º) el tiempo transcurrido desde que dejó de actuar el momento de rotación de las fuerzas hasta que el volante se paró por completo. Sol. 1) 308 N.m; 2) 97 s. 7.5) Un volante comienza a girar con una aceleración constante α = 0,5 rad/s2 y después de un tiempo t1= 15 s de haber empezado a moverse adquiere un momento de la cantidad de movimiento L = 73,5 kg.m2/s. Hallar la energía cinética que tendrá este volante al cabo de un tiempo t2= 20 s de haber empezado la rotación. Sol. 490 J. 7. Dinámica de rotación 44 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 7.6) Por un plano inclinado formado por dos carriles de altura h = 0,9 m e inclinación pequeña, rueda sin deslizar un cilindro de radio r y masa M = 72 kg, que lleva solidario otro coaxial de radio R = 6r y masa M 248 kg. Se supone que este conjunto se abandona sin velocidad inicial en la parte más elevada del plano. Calcular la velocidad de traslación cuando ha descendido h sobre la vertical. Sol. 1,08 m/s. 0,9 m m 7.7) Una plataforma horizontal de 100 kg de masa gira alrededor de un eje vertical que pasa por su centro y da 10 r.p.m. Un hombre que pesa 60 kgf se encuentra en estas condiciones en el borde de la plataforma. ¿Con qué velocidad comenzará a girar la plataforma si el hombre se traslada desde el borde hacia el centro de la misma? Considerar que la plataforma es un disco circular homogéneo y que el hombre es una masa puntual. Sol. 22 r.p.m. 7.8) Hallar la energía cinética de un ciclista que marcha con la velocidad v = 9 km./h. El peso del ciclista con la bicicleta es P = 78 kgf, con la particularidad de que a las ruedas les corresponde un peso P1= 3 kgf. Considerar que las ruedas son aros. Sol. 263 J. 7.9) Un volante de radio R = 0,2 m y masa m = 10 kg está unido a un motor por medio de una correa de transmisión. La tensión de la correa, que se mueve sin deslizamiento, es constante e igual a T = 14,7 N. ¿Qué número de r.p.m. dará el volante al cabo de un tiempo t = 10 s, después de comenzar el movimiento? Considerar que el volante es un disco homogéneo. El rozamiento se desprecia. Sol. 1.403 r.p.m. 7. Dinámica de rotación 45 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 7.10) Un cilindro puede rodar sin rozamiento ni deslizamiento sobre un plano inclinado 30º y está unido por medio de un hilo ideal que pasa por una polea sin masa y sin rozamiento a otra masa igual a la cuarta parte de la suya, como se indica en el esquema. Calcular la velocidad con que este cilindro baja por el plano inclinado, cuando partiendo del reposo, la masa menor ha ascendido 0,7 m. Sol. 1,4 m/s. M = 4m m 30º 7.11) Se tiene un volante de radio R = 1 m y una masa M = 100 kg se supone localizada en la llanta. Arrollada a su eje cuyo radio es r = 10 cm y masa despreciable hay una cuerda de la que pende un cuerpo de masa m = 40 kg, este cuerpo está a una altura h = 18 m del suelo. Calcular: 1) La aceleración con que cae el cuerpo. 2) La tensión de la cuerda durante la caída. 3) Tiempo que tarda el cuerpo en llegar al suelo. 4) Energía cinética adquirida por el volante al llegar al suelo. Sol. 1) 0,04 m/s2. 2) 390,4 N. 3) 30 s. 4) 7.200 J. 7.12) Un cilindro macizo y homogéneo de 1 metro de radio y 100 kg de masa tiene su eje, también macizo y homogéneo, de 10 cm de radio y 10 kg de masa. Tangencialmente al eje se aplica una fuerza de 1 N durante 10 minutos. Calcular la velocidad angular en vueltas por minuto. Sol. 11,4 r.p.m. 7.13) En la parte superior de un doble plano inclinado, siendo α = 30º para ambos planos, hay una polea ideal sin masa ni rozamiento, por la que pasa un hilo ideal. En uno de los extremos del hilo hay una masa m, que desliza sobre su plano con un coeficiente de fricción µ = 0,1 y en el otro un cilindro de masa doble que se puede mover sobre el plano rodando sin deslizamiento ni rozamiento, pues el de rodadura se considera despreciable. Determinar si el cilindro asciende o desciende y la velocidad lineal cuando se ha desplazado un metro a lo largo del plano, partiendo del reposo. Sol. El cilindro desciende, 1,42 m/s. 7.14) Un volante gira con una velocidad constante correspondiente a v = 10 r.p.s. y su energía cinética W0= 800 kgm. ¿Cuánto tiempo tardará un momento de fuerzas de rotación M = 50 N.m aplicado a este volante en aumentar al doble su velocidad angular? Sol. 5 s. 7. Dinámica de rotación 46 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería 7.15) Torrelavega Un aro y un disco, cuyos pesos P son iguales, ruedan sin resbalar con velocidades lineales v iguales. La energía cinética del aro W 1= 4 kgm. Hallar la energía cinética W 2 del disco. Sol. 29,4 J. 7.16) Un disco uniforme de radio R = 12 cm y masa M = 400 g está montado sobre un eje apoyado sobre cojinetes sin fricción. Alrededor de su borde se encuentra arrollada una cuerda de la que cuelga un cuerpo de masa m = 50 g. Calcular: a) la velocidad de m cuando ha descendido 50 cm partiendo del reposo, b) la tensión de la cuerda. Sol. a) 1,4 m/s; b) 0,39 N. 7.17) Un cuerpo con el radio R y la masa m rueda horizontalmente sin deslizarse con velocidad v. Después rueda hacia arriba por un plano inclinado, hasta una altura máxima h. Si h = 3v2/4g, a) ¿Cual es el momento de inercia del cuerpo? b) ¿De que cuerpo se trata?. Sol. a) 1/2 mR2; b) cilindro macizo. 7.18) Una polea fija y otra móvil están montadas como indica la figura. Las dos poleas se consideran como cilindros macizos y homogéneos y pesan 1 kilo cada una; el hilo es ideal. La masa que pende de la polea móvil pesa también 1 kilo, y la que cuelga del extremo del hilo 1/2 kilo. Calcular la velocidad de la masa M cuando está a 2 metros de distancia de su posición inicial y su energía cinética en kilográmetros. Sol. 2,46 m/s; 0,308 kgm. MF r m M 7. Dinámica de rotación 47 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 7.19) Un disco gira alrededor de un eje vertical dando 30 r.p.m. Sobre este disco y a 20 cm de distancia del eje de rotación se encuentra un cuerpo. ¿Que valor deberá tener el coeficiente de rozamiento entre el cuerpo y el disco para que aquel no se deslice fuera de éste? Sol. 0,2 7.20) Un disco que pesa 2 kgf rueda sin resbalar por un plano horizontal con la velocidad de 4 m/s. Hallar la energía cinética del disco. Sol. 24 J. 7.21) Dos pesas cuyos pesos son distintos están unidas entre sí por un hilo que pasa por una polea. El momento de inercia de la polea es I = 50 kg.m2 y su radio R = 20 cm. La polea se mueve con rozamiento y el momento de las fuerzas de rozamiento Mr = 98,1 N.m. Hallar la diferencia que hay entre las tensiones del hilo T1- T2 por ambos lados de la polea, sabiendo que esta última gira con una aceleración angular constante α = 2,36 rad/s2 Sol. 1.080 N. 7.22) Un disco gira alrededor de un eje vertical dando 30 r.p.m. Sobre este disco y a 20 cm de distancia del eje de rotación se encuentra un cuerpo. Que valor deberá tener el coeficiente de rozamiento entre el cuerpo y el disco para que aquel no se deslice fuera de éste. Sol. 0,2. 7.23) Un volante está construido con un disco macizo de 0,5 m de diámetro y 0,02 m de espesor, y de dos ejes que sobresalen, de 0,1 m de diámetro y 0,1 m de longitud. Si el material de que está formado tiene densidad de 6.000 kg./m3, hállese su momento de inercia respecto al eje de rotación. Sol. 0,75 kg.m2. 7.24) Una plataforma gira alrededor de un eje vertical, dando una vuelta cada 10 segundos. El momento de inercia de la plataforma respecto a este eje es 1.200 kg.m2. Un hombre de 80 kg de masa se encuentra inicialmente de pie en el centro de la plataforma y comienza a andar a lo largo de un radio. ¿Cuál es la velocidad angular de la plataforma cuando el hombre se ha alejado 2 m del centro? Sol. 0,0789 r.p.s. 7. Dinámica de rotación 48 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería 7.25) Torrelavega Una plataforma horizontal de 100 kg de masa gira alrededor de un eje vertical que pasa por su centro y da 10 r.p.m. Un hombre que pesa 60 kgf se encuentra en estas condiciones en el borde de la plataforma. ¿Con qué velocidad comenzará a girar la plataforma si el hombre se traslada desde el borde hacia el centro de la misma? Considerar que la plataforma es un disco circular homogéneo y que el hombre es una masa puntual. Sol. 22 r.p.m. 7.26) Un disco de acero de 2,5 kg y 20 cm de diámetro, se fija a un eje de 1,5 kg de masa y 5 cm de diámetro. El eje se apoya en rieles que forman un ángulo de 30º con la horizontal y se desliza sobre ellos sin resbalar. Calcular: a) El momento de inercia del sistema disco eje. b) La aceleración lineal del centro del disco cuando el sistema gira. Sol. a) 0.013 kg.m2; b) 0,79 m/s2. l h 30º 7.27) Lanzamos hacia arriba rodando por un plano inclinado de 30º una esfera maciza. Su centro de gravedad lleva al salir una velocidad de 5 m/s. Calcular: a) Altura que alcanzará la esfera; b) Tiempo que tardará en regresar al plano horizontal Sol. a) 1,79 m; b) 1,21 s. 7. Dinámica de rotación 49 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería 7.28) Torrelavega Una varilla uniforme de acero con longitud de 1,2 m y masa de 6,4 kg se encuentra unida en cada extremo a una pequeña bola que tiene la masa de 1,06 kg. La varilla está obligada a girar en un plano horizontal alrededor de un eje vertical que pasa por su punto central. Se observa que en cierto instante se encuentra girando con una velocidad angular de 39 r.p.s. Debido a la fricción del eje, queda en reposo 32 s después. Calcular: a) la aceleración angular, b) el momento de fricción ejercido por el eje, c) el trabajo total hecho por la fricción del eje y d) el número de revoluciones que se llevan a cabo durante los 32 s. Sol. a) 7,66 rad/s2, b) 11,72 N.m, c) 4,59x104 J, d) 624 rev. 7.29) Dos masas iguales, cada una de 0,10 kg se fijan en los extremos de una varilla muy ligera de 1 m de longitud, que está sostenida en el centro por un pivote sin fricción, como se indica en la figura. El mecanismo interno de la varilla puede mover las masas hacia el centro a lo largo de la varilla. El sistema gira con una velocidad angular de 8 rad/s con las masas en los extremos de la varilla. Si se pone a trabajar el mecanismo interno de la varilla y las masas se mueven para que estén a 0,25 m del centro, cada una, ¿Cuál será la velocidad angular del sistema y cuales serán las Ec inicial y final de éste? Sol. 32 rad/s; Ec 1= 1,6 J; Ec 2= 6,4 J. 7.30) La velocidad de rotación de una rueda que gira con movimiento uniformemente retardado por haber sido frenada, disminuye en 1 min. desde 300 hasta 180 r.p.m. El momento de inercia de la rueda es igual a 2 kg.m2. Hallar 1) la aceleración angular de la rueda, 2) el momento decelerador (de la fuerza que la frena) 3) el trabajo de frenado y 4) el número de vueltas que da la rueda en este minuto. Sol. 1) 0,22 rad/s2, 2) 0,44 N.m, 3) 655 J, 4) 237 rev. 7.31) Una polea cuyo peso P = 1 kgf está sujeta en el borde de una mesa. Las pesas A y B pesan lo mismo P1= P2= 1 kgf, y están unidas entre sí por un hilo que pasa por la antedicha polea. El coeficiente de rozamiento de la pesa B con la mesa es K = 0,1. Considerando que la polea es un disco homogéneo y depreciando su rozamiento, hallar: 1) la aceleración con que se mueven las pesas y 2) las tensiones T1 y T2 de las ramas del hilo. Sol. 3,53 m/s2, T1= 0,46 kgf, T2= 0,64 kgf. 7. Dinámica de rotación 50 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 7.32) Una masa de 5 kg está sostenida por un plano inclinado sin fricción, como se muestra en la figura. La masa está fija a una cuerda delgada que está enrollada en un cilindro homogéneo de 4 kg de masa y 30 cm de radio. Cuando el sistema parte del reposo, calcular: a)la aceleración de la masa, b) la energía cinética de la masa después de haberse movido 5 m. Sol. a) 4,2 m/s2, b) 105 J. 5 kg h 37º 7.33) Una piedra de afilar tiene forma de cilindro macizo, con 0,5 m de radio y 50 kg de masa. a) Si parte del reposo, ¿qué momento le comunicará en 10 s una velocidad angular de 300 r.p.m. b) Cual es su energía cinética cuando gira a 300 r.p.m. Sol. a) 19,63 N.m, b) 3.081 J. 7.34) Una masa de 2 kg está sostenida por un hilo sin masa enrollado en una polea cuyo diámetro es 0,80 m y su momento de inercia es de 0,60 kg.m2. Si el sistema inicialmente está en reposo, ¿cuales son la tensión en el hilo, la velocidad de la masa de 2 kg y la energía cinética total del sistema cuando la masa de 2 kg ha alcanzado un punto exactamente a 3 m bajo su punto de partida? ¿Cuánto tiempo habrá pasado desde que arranca y el instante en que pasa por este punto la masa de 2 kg? Sol. Ec=58,8 N; T=12,8 N. 7.35) Un bloque de masa m = 5 kg desliza por una superficie inclinada 37º con la horizontal, como se indica en la figura. El coeficiente cinético de rozamiento es de 0,25. Se enrolla una cuerda unida al bloque alrededor de un volante cuyo eje fijo pasa por O. El volante tiene una masa M = 20 kg y su radio exterior R = 0,2 m. a) ¿Con qué aceleración desliza el bloque por el plano? b) ¿Cuál es la tensión de la cuerda? -2 Sol. a) 1,97 m.s ; b) 9,85 N. 5 kg 37º 7. Dinámica de rotación 51 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 7.36) Una masa de 3 kg se fija a un cordón largo sin masa que está enrollado a un tambor. El tambor gira en un eje horizontal fijo sobre cojinetes sin fricción. Sabiendo que la tensión en el cordón es de 10 N, calcular; a) el momento de inercia del tambor, b) que fracción de la energía total del sistema se debe a la rotación del tambor, si la velocidad de la masa de 3 kg es de 4 m/s. Sol. a) I=0,247 kg.m2; b) 0,34. 7.37) Una masa m1 = 1 kg cuelga del extremo de una cuerda sin peso, que pasa por una polea sin rozamiento y después se arrolla en un cilindro de masa m2 = 8 kg y radio r = 10 cm que rueda sobre un plano horizontal. Hallar: 1º) La aceleración de la masa m1. 2º) La tensión de la cuerda. 3º) La aceleración angular del cilindro. Recordar que aA = a0 + αr Sol. 1º) 2,45 m/s2; b) 7,35 N; c) 12,25 rad/s2. m2 r o m1 7.38) Un tanque se pone en movimiento por el motor que hace rodar cuatro ruedas (dos en cada lado). Las ruedas con sus salientes agarran las orugas. Determinar la velocidad del tanque, pasados 10 s de haberse puesto en marcha este último, si la potencia útil media del motor P = 200 kw, la masa del tanque M1 = 10.000 kg, la masa de cada oruga M2 = 700 kg, la masa de cada rueda M3 = 200 kg. Considerar las ruedas como cilindros homogéneos. Sol. 16,9 m/s; 60,8 km/h. 7. Dinámica de rotación 52 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 7.39) En el instante t = 0 s las masas M y m del sistema se encuentran como se indica en la figura. La polea P se puede considerar sin masa, y el radio de giro de la polea doble es RG = 0,4 m. Si el sistema se deja en libertad en la posición anterior, determinar: a) Las tensiones de las cuerdas, sabiendo que el coeficiente de rozamiento sobre la horizontal es 0,2; b) Distancia recorrida por la masa M después de t = 2 s. Sol. T1 = 108,8 N, T2 = 129 N, s = 1,24 m MP=50 kg r=0,2 m RG R=0,35 m R P M=50 kg m=10 kg 7.40) Una masa de 2 kg está sostenida por un hilo sin masa enrollado en una polea cuyo diámetro es de 0,80 m y su momento de inercia es de 0,60 kg.m2. Si el sistema inicialmente está en reposo, ¿cuáles son la tensión en el hilo, la velocidad de la masa de 2 kg y la energía cinética total del sistema cuando la masa de 2 kg ha alcanzado un punto exactamente a 3 m bajo su punto de partida? ¿Cuánto tiempo habrá pasado desde que arranca y el instante en el que pasa por este punto la masa de 2 kg? Sol. T = 12,8 N, ECT = 58,8 J, t = 1,33 s 7. Dinámica de rotación 53 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 7.41) Una polea recibe la rotación de la otra polea (conductriz) mediante la transmisión por correa. El ramal conductriz de la correa está tensado con una fuerza T = 98 N, el ramal conducido, con una fuerza t = 49 N. La masa de la polea M = 200 kg, su diámetro D = 0,4 m. Determinar la aceleración angular de la polea, tomando en consideración el rozamiento del árbol en los cojinetes. El diámetro del árbol d = 0,06 m, el coeficiente de rozamiento µ = 0,1. Del peso del árbol se puede prescindir. La polea se considerará un cilindro macizo homogéneo. Sol. α = 0,98 rad/s2. t d D F T 7.42) Un cuerpo de masa m1 = 10 kg y coeficiente cinético de rozamiento 0,85, desliza por una superficie inclinada 30º con la horizontal. Este cuerpo se une por medio de una cuerda, sin masa, a otro cuerpo de masa m2 = 20 kg como se indica en la figura. La cuerda pasa por una polea maciza de masa 15 kg y radio R = 0,2 m que tiene un eje de 5 cm de radio y cuyo coeficiente de rozamiento dinámico entre el eje y el cojinete es 0,15. Calcular: a) ¿Con qué aceleración desliza el bloque por el plano? b) ¿Cuál es la tensión de la cuerda? Sol. a) a = 9,24 m/s2; b) T = 214 N M=15 kg 49 N m 2=20 kg 30º 7.43) Un disco uniforme con una masa de 120 kg y un radio de 1,4 m rueda inicialmente con una velocidad angular de 1.100 rev/min. a) A una distancia radial de 0,6 m se aplica una fuerza tangencial. ¿Qué trabajo debe realizar esta fuerza para detener el disco? b) Si la rueda se detiene en 2,5 min., ¿Qué momento produce la fuerza? ¿Cuál es la magnitud de la fuerza? c) ¿Cuántas revoluciones da la rueda en estos 2,5 min.? Sol. a) 777.630 J; b) M = 90,6 N.m, F = 151 N; c) 1.367 rev. 7. Dinámica de rotación 54 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 7.44) Una rueda pose una delgada llanta de 3,0 kg y cuatro radios, cada uno de masa 1,2 kg. Determinar la energía cinética de la rueda al rodar sobre una superficie horizontal a la velocidad de 6,0 m/s. Sol. 223 J 7.45) Las ruedas de una bicicleta tienen un radio de 35 cm y una masa de 0,6 kg cada una. La bicicleta acelera uniformemente de 0 a 36 km/h en 100 s. a) Hallar la aceleración angular de las ruedas; b) hallar la energía cinética total de las ruedas en el instante t = 100 s (se considera que el 25 % de la masa de la rueda se concentra en la llanta y el 75 % en el eje; c) repetir el apartado anterior si las ruedas son lenticulares (la masa de la rueda se considera distribuida de forma uniforme en todo el disco). Sol. a) 0,29 rad/s2; b) 37,5 J; c) 45 J 7.46) Dos cilindros homogéneos de 10 kg de masa cada uno, se pegan para formar el mecanismo de la figura, que puede girar sin rozamiento respecto al eje que está unido a la pared. Los radios de los cilindros son R 0,4 m y r = 0,1 m. Del cilindro mayor radio se cuelga un bloque de 12 kg y del de menor radio uno de 24 kg. Dibujar todas las fuerzas sobre la polea. Explica por qué el conjunto gira en el sentido contrario a las agujas del reloj (sin resolver el sistema de ecuaciones). Cuando la masa de 12 kg ha descendido 1 m partiendo del reposo, ¿cuánto ha ascendido la de 24 kg? Calcular la velocidad del bloque de 12 kg en ese instante. ¿Qué utilidad puede tener un mecanismo de este tipo? Sol. La masa de 12 kg desciende; 0,25 m; 2,5 m/s; Para elevar grandes pesos. N R Eje de giro r P T1 T2 12 24 7. Dinámica de rotación 55 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 7.47) El objeto de la figura es macizo y homogéneo; las masas de los cilindros son M1 = M2 = 2.500 kg y M2 = 69,5 kg; sus radios son R1 = R3 = 0,6 m y R2 = 0,1 m. a) hallar su momento de inercia respecto al eje OO’ y respecto al eje AA’; b) hallar la velocidad angular si el objeto gira respecto a OO’ con momento angular L = 20 kg m2/s; c) hallar el tiempo que el objeto tarda en hundirse en un lago de 40 m de profundidad partiendo del reposo (despreciar rozamientos). 2 2 Sol. a) Ioo’= 900,3 kg m , IAA’= 5.969,8 kg m ; b) L = 0,022 rad/s; c) t = 3 s O A R1 h1=0,2 m M1 R2 M2 h2=0,2 m h3=0,2 m R3 M3 d=1 m A’ O’ 7. Dinámica de rotación 56 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 8. ELASTICIDAD FORMULARIO Tracción : Variación de la longitud ∆l 1 F = l E S Variación de la sec ción transversal ∆r σF =− r E S ∆r ∆l = −σ r l Compresibilidad : ∆V P =− V Q E 3(1 − 2σ ) dV 1 =− ∆P Gases : Adiabática γP V dV 1 = − ∆P Isoterma V P 3 4 l 1 l3 ' = Flexión : s = C f F Cf = C f 4E b d 3 E bd3 1F E µ= Cizalla : α = µS 2(1 + σ) Sólidos : Torsión : 8. Elasticidad β= 1 M R M = Q= πµβr4 2l R= 57 π r4 µ 2l QA = γ P QT = P Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 8.1) ¿Que diámetro mínimo debe tener un cable de acero para poder aguantar 1 Tmf de carga? Sol. 4x10-3 m Resistencia a la rotura ER= 7,85x108 N.m-2 8.2) Desde un barco se lanzó una pesa sujeta a un cable de acero para medir la profundidad del mar. Despreciando el peso de la pesa en comparación con el cable, hallar la profundidad máxima que se puede medir por este procedimiento. La densidad del agua del mar tómese igual a 1 g/cm3. Sol. 11.956 m Densidad del acero = 7.700 kg/m3 ER= 7,85x108 N.m-2 8.3) Del tejado de una casa cuelga un alambre de acero de 40 m de longitud y 2 mm de diámetro 1) ¿Qué carga máxima se puede colgar de este alambre sin que llegue a romperse? 2) ¿Cuánto se alargará este alambre si de él cuelga un hombre que pesa 70 kgf? 3) ¿Se notará alargamiento permanente cuando el hombre antedicho suelte el alambre? El límite de elasticidad del acero tómese igual a 2,94x108 N.m-2. Módulo de Young = 21,6x1010 N.m-2. Límite de rotura ER= 7,85x108 N.m-2. ρ = 7.700 kg.m-3. Sol. 1) 250 kgf; 2) 40x10-3 m; 3) No porque la carga específica es menor que el límite de elasticidad. 8.4) De un alambre de acero de 1 mm de radio hay colgada una carga de 981 N. ¿Qué ángulo se puede desviar el alambre con el peso sin que al soltarlo se rompa aquel al pasar la carga por la posición de equilibrio? Sol. 75º 55' ER= 7,85x108 N.m-2. 8.5) Una pesa de 1 kgf está atada a un alambre de hierro de 50 cm de longitud y de 1 mm de diámetro. ¿A que número máximo de revoluciones por segundo se puede hacer girar el alambre con la pesa, en el plano vertical, sin que aquel llegue a romperse? Sol. 3,4 r.p.s. ER= 2,94x108 N.m-2 8. Elasticidad 58 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 8.6) Para hacer un tirador se ha empleado un cordón de goma de 42 cm de longitud y 3 mm de radio. El niño que dispara con él estira la goma 20 cm al lanzar la piedra. Hallar el módulo de Young de esta goma sabiendo que una piedra cuyo peso era de 0,02 kgf salió disparada por el tirador con la velocidad de 20 m/s. La variación que experimenta la sección del cordón al estirarse se desprecia. Sol. 1,49x106 N.m-2. 8.7) Una correa sin fin va a la velocidad de v = 15 m/s y transmite el movimiento de un motor de potencia 40 C.V. Tiene un coeficiente de rotura de ER= 250 kg cm-2 y un ancho de a = 9 cm. ¿Que espesor ha de tener, si el coeficiente de seguridad es K = 9? Sol. 0,8 cm. 8.8) Un cable de 2 metros de longitud está formado por otros tres de secciones S1= 1, S2= 2, S3= 3 milímetros cuadrados y cuyos módulos de Young son E1= 20x103, E2= 15x103 y E3= 10x103 kp.mm-2. Se fija por un extremo y en el otro se pone una masa M = 100 kg. Calcular el alargamiento que experimenta y las cargas parciales que cada uno soporta. Sol. 2,5 mm; F1= 25 kp; F2= F3= 37,5 kp. 8.9) Una barra de acero, cuya sección es un rectángulo de 0,5x2 cm, tiene una longitud de 50 cm. El módulo de Young vale E = 2x104 kp/mm2. Calcular la flecha cuando se suspende un peso de 1 kg. 1º) Del extremo estando la barra horizontal y fija por el otro y a) con las caras menores horizontales y b) con las caras mayores horizontales, 2º) Del punto medio estando horizontal y apoyada en sus extremos en los dos casos anteriores a) y b). Sol. 1º) a) 10 mm, b) 0,63 mm; 2º) a) 0,63 mm, b) 0,04 mm 8.10) Se quiere levantar un cuerpo que pesa 80 Tm y se dispone para ello de cable de acero de un coeficiente de rotura ER= 100 kg.mm-2 y sección 20 mm2. Se toma un coeficiente de seguridad igual a 6. Se quiere, con el cable disponible, trenzándolo, fabricar otros 6 más gruesos, con los que se ha de realizar la operación. ¿Cuantos cabos compondrán cada cable? Sol. 40 cabos. 8.11) Hallar la longitud que tendrá un alambre de cobre que colgando verticalmente comience a romperse por su propio peso. Sol. 2.906 m. Carga de rotura = 2,45x108 N.m-2 Densidad = 8.600 kg.m-3 8. Elasticidad 59 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería 8.12) Torrelavega Para sacar agua de un pozo se dispone de un cubo metálico, cuya masa es de 9 kg y capacidad 25 l. El cubo se ata a una cuerda de cáñamo que solo puede soportar 1,5 kp.mm-2. ¿Cuál ha de ser la sección de esta cuerda, si el pozo tiene 25 metros de profundidad? Sol. 23 mm2. La densidad de la cuerda es 2 g.cm-3. 8.13) Calcular la longitud máxima de un tubo de cobre que puede colgarse sin romperse, por uno de sus extremos. Sol. 3.370,79 m. Densidad del cobre 8,9 g.cm3. Carga de rotura 30 kp.mm-2. 8.14) Una barra homogénea de 100 kg, está suspendida en posición horizontal por tres alambres de la misma longitud y sección, el central es de acero y los de los extremos de cobre, de módulo de Young mitad que el de acero. Determinar la tensión de los alambres. Sol. Fa = 50 kg.; Fc = 25 kg. 8.15) ¿Que longitud habría de darse a un alambre de cobre para que se rompa por su propio peso? La densidad del cobre es ρ = 8,9 g.cm-3 y su coeficiente de rotura ER= 30 kp.mm-2. Sol. 3.370,8 m. 8.16) Un péndulo está formado por un hilo de acero de 5 m de longitud y 1 mm2 de sección con una esfera en un extremo de M = 50 kg. Se le desvía de la vertical un ángulo de ϕ = 10º. ¿Cuál es la longitud del hilo cuando pasa por la vertical? E = 20.000 kp.mm-2. Sol. 5,0129 m. 8.17) Un galvanómetro de espejo lleva suspendido éste de un fino hilo de plata de l = 10 cm y 0,08 mm de diámetro. El espejo refleja la luz de una rendija cuya imagen se forma en una escala que dista s = 1,8 m del espejo y en ella se aprecian desplazamientos de milímetros. ¿Que par mínimo se podrá medir? µ = 3.000 kp.mm-2. Sol. 0,00328 Dinas.cm. 8.18) Una masa de 1 kg está en el extremo de una varilla de 0,5 m de longitud y un centímetro cuadrado de sección. Esta varilla es horizontal y gira alrededor de un eje vertical que pasa por su otro extremo. El módulo de Young de la misma es E = 103 kp.mm-2. ¿Cuál debe ser la velocidad angular en vueltas por minuto, para que esta varilla se alargue en su centésima parte? Despréciese la masa de la varilla. Sol. 1.337 r.p.m. 8. Elasticidad 60 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 8.19) Con un hilo metálico de densidad 7,5 g.cm-3, que ha de soportar ER= 25 kg.mm2, se quiere elevar desde el fondo de un pozo de h = 1.667 m de profundidad hasta la boca, un peso P = 5 Tm. ¿Que sección ha de tener el hilo? Sol. 400 mm2. 8.20) Una masa de 15 kg sujeta de un extremo de un alambre de acero cuya longitud sin estirar es de 0,5 m, gira en un círculo vertical con velocidad angular de 2 r.p.s. en el punto más bajo de su trayectoria. La sección transversal del alambre es 0,02 cm2. Calcular el alargamiento del alambre cuando el peso se encuentra en el punto más bajo de su trayectoria. Módulo de Young del acero E = 19.000 kg.mm-2. Sol. 1,79 mm. 8.21) Una masa de un kilogramo está en el extremo de una varilla de 0,5 m de longitud y un centímetro cuadrado de sección. Esta varilla es horizontal y gira alrededor de un eje vertical que pasa por su otro extremo. El módulo de Young de la misma es E = 103 kp/mm2. ¿Cuál debe ser la velocidad angular, en vueltas por minuto, para que esta varilla se alargue en su centésima parte? Despréciese la masa de la varilla. Sol. 1.337 r.p.m. 8.22) Una varilla de cobre de 2 m de longitud y 2 cm2 de sección se une a otra de acero de longitud L y 1 cm2 de sección transversal. La varilla resultante se somete en sus extremos a tracciones opuestas de 3x104 N. a) Hállese la longitud L de la varilla de acero, si los alargamientos de ambas varillas son iguales. b) ¿Cuál es el esfuerzo en cada varilla? c) ¿Cuál es la deformación en cada varilla? Módulo de Young: cobre 1,1x1011 Pa; acero 2x1011 Pa Sol. a) 1,82 m; b) 1,5x108 Pa, 3x108 Pa; c) 2,73x10-3 m, 2,73x10-3 m 8.23) Una barra homogénea de 100 kg, está suspendida en posición horizontal por tres alambres de la misma longitud y sección, el central es de acero y los de los extremos de cobre, de módulo de Young mitad que el del acero. Determinar la tensión de los alambres. Sol. Ta 50 kg; Tc 25 kg. 8. Elasticidad 61 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 8.24) Una masa de 3 kg parte del reposo en un plano inclinado de 2 m, como muestra la figura. En la parte inferior del plano hay un resorte, S, cuya constante de elasticidad es 1x104 N/m. El coeficiente de fricción cinética entre el plano y la masa es de 0,3; entre los puntos A y B, el coeficiente de fricción es cero. Calcular a) la velocidad de la masa exactamente antes de hacer contacto con el resorte; b) la compresión máxima del resorte; c) la altura a la cual sube la masa después de rebotar con el resorte. Sol. a) 4,34 m/s; b) 0,0767 m; c) 0,63 m. 3 kg A 2m 30º B 8.25) Una viga AB de longitud l = 6 m y peso 800 kp está fija en A y forma con la horizontal un ángulo de 60º gracias al cable y el muelle BC, que une el extremo B de la viga con el punto C del suelo. Sabiendo, que la constante del muelle es K = 5x106 N/cm y que la distancia AC es 4 metros, calcular: a) El alargamiento del muelle b) La reacción en A c) El ángulo γ que forma el conjunto cable muelle con la horizontal Sol. a) ∆x= 9,8x10-4 cm; b) F=1.172,1 kp; c) γ = 36,59º B T h 6m γ C 8. Elasticidad 60º 4m A 62 D Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 8.26) Una masa de 0,5 kg se sujeta a un alambre de aluminio de diámetro 1,6 mm y longitud sin deformar 0,7 m. El otro extremo del alambre está fijo a un poste. La masa gira alrededor del poste en un plano horizontal con una velocidad de rotación tal que el ángulo que forman el alambre y la vertical es 5,0º. Determinar la tensión del alambre y su longitud. Módulo de Young del aluminio 7x108 N/m2. 8.27) Un bloque de 4 kg cuelga de una cuerda ligera que a través de una polea sin rozamiento está conectada a un bloque de 6 kg que descansa sobre una plataforma rugosa. El coeficiente de rozamiento cinético es µc= 0,2. El bloque de 6 kg se empuja sobre un muelle, al cual no está sujeto. El muelle tiene una constante de dureza de 180 N/m y se comprime 30 cm. Determinar la velocidad de los bloques cuando el muelle se libera y el bloque de 4 kg cae una distancia de 40 cm. Sol. v = 1,95 m/s m1=6 kg m2=4 kg 8. Elasticidad 63 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 9. CHOQUES FORMULARIO Choque elástico : v1' = 2 m2 m − m2 v2 + 1 v m1 + m2 m1 + m2 1 Choque inelástico : v' = m1v m1 + m2 Coeficiente de restitución : 9. Choques c=− 2 g h2 − 2 g h1 64 = v2' = h2 h1 2 m1 m − m2 v1 − 1 v m1 + m2 m1 + m2 2 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 9.1) Un proyectil de masa 0,05 kg, que se mueve con una velocidad de 400 m/s penetra una distancia de 0,1 m en un bloque de madera firmemente sujeto al suelo. Se supone que la fuerza deceleradora es constante. Calcular: a) la deceleración del proyectil; b) la fuerza deceleradora; c) el tiempo que dura la deceleración; d) la impulsión del choque. Compárese la respuesta del apartado d) con la cantidad de movimiento inicial del proyectil. Sol. a) 800.000 m.s-2, b) 40.000 N, c) 5x10-4 s, d) 20 N/s, 20 kg.m/s. 9.2) Dos bloques de masas 300 g y 200 g se mueven uno hacia el otro sobre una superficie horizontal lisa con velocidades de 50 cm/s y 100 cm/s, respectivamente. a) Si los bloques chocan y permanecen unidos, calcular su velocidad final. b) Calcular la pérdida de energía cinética durante el choque. c) Calcular la velocidad final de cada bloque si el choque es perfectamente elástico. Sol. a) 10 cm/s; b) 0,135 J; c) 80 cm/s, d) -70 cm/s. 9.3) Un automóvil de 2,000 kg que avanza a lo largo de una calle, en dirección ESTE, choca, a la velocidad de 60 km/h, con un camión que pesa 4 Tm y que atraviesa la misma calle en dirección SUR a la velocidad de 20 km/h. Si como consecuencia del choque quedan unidos, ¿cual es la magnitud y dirección de su velocidad inmediatamente después del choque? Sol. 24 km/h, 56º 18' S-E. 9.4) Una bala de rifle, de masa 10 g, choca contra un bloque de masa 990 g que se encuentra en reposo sobre una superficie horizontal lisa, yEqueda incrustada en él. El bloque está unido a un resorte en hélice como se indica en la figura, y el choque comprime el resorte 10 cm. El calibrado del resorte indica que para comprimirlo 1 cm es necesaria una fuerza de 100.000 dinas. a) Calcular la energía potencial máxima del resorte. b) Calcular la velocidad del bloque justamente después 6 del choque. c) ¿Cual era la velocidad inicial de la bala? 4 Sol. a) 5x10 ergios; b) 100 cm/s; c) 10 cm/s. 9.5) Un cañón de 600 kg, montado sobre ruedas, dispara un proyectil de 4 kg con una velocidad inicial de 600 m/s y un ángulo de elevación de 30º. Calcular la velocidad horizontal de retroceso del cañón. Sol. 3,44 m/s. 9. Choques 65 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 9.6) Se dispara una bala de 25 g contra un bloque de 5 kg de madera suspendido de una cuerda, quedando la bala incrustada en él. Sabiendo que el centro de gravedad del bloque se desplaza 10 cm hacia arriba, calcular la velocidad inicial de la bala. Sol. 281 m/s. 9.7) Un tractor de 6 Tm que viaja hacia el norte con una velocidad de 25 km/h choca con otro de 4 Tm que se dirige hacia el oeste con una velocidad de 70 km/h. Sabiendo que los dos vehículos permanecen juntos después del choque, hallar la velocidad y dirección de ambos vehículos inmediatamente después del choque. Sol. 31,8 km./h. 9.8) Una bola se deja caer sobre un suelo horizontal y alcanza una altura de 144 cm después del primer rebote; en el segundo rebote llega a 81 cm de altura. Calcular: a) el coeficiente de restitución entre la bola y el suelo, b) la altura que alcanzaría en un tercer rebote. Sol. a) 0,75; b) 46 cm. 9.9) Un cañón cuya masa es de 5x103 kg dispara un proyectil que pesa 100 kgf. La energía cinética del proyectil al salir del cañón es igual a 7,5x106 J. ¿Qué energía cinética adquirirá el cañón a causa del retroceso? Sol. 1,5x105 J. 9.10) Supongamos una escopeta de juguete, con el eje de disparo horizontal, a una altura de 1,8 m del suelo. A una distancia de 4 m se encuentra una pared vertical. Si presionamos el muelle una distancia de 0,1 m y colocamos una masa de 200 g, calcular la constante K del muelle si el cuerpo choca con la pared, (coeficiente de restitución e = 0,5) a una altura de 1 m y en qué punto del suelo cae. Sol. 1.648,9 N/m; 0,86 m. 9. Choques 66 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 9.11) Un bloque de masa m1 = 1,6 kg moviéndose hacia la derecha con una velocidad de 4 m/s sobre un camino horizontal sin fricción, choca contra un resorte sujeto a un segundo bloque de masa m2= 2,1 kg que se mueve hacia la izquierda con una velocidad de 2,5 m/s, como en la figura. El resorte tiene una constante de fuerza de 600 N/m. En el instante en que m1 se mueve hacia la derecha con una velocidad de 3 m/s, determine: a) la velocidad de m2 y b) la distancia x que se comprimió el resorte. Sol. x = 0,173 cm v 1 i= 2,5 m/s v 1 i = 4 m/s m2 m1 v2f v 1 f i = 3 m/s m2 m1 x 9.12) Un bloque de masa m1 = 2 kg se desliza a lo largo de una mesa sin rozamiento con una velocidad de 10 m/s. Directamente enfrente de este bloque y moviéndose en la misma dirección con una velocidad de 3 m/s hay otro bloque de masa m2 = 5 kg, conectado a un muelle de masa despreciable y constante de fuerza k = 1120 N/m, como se muestra en la figura. a) Antes de que m1 choque contra el muelle, ¿cuál es la velocidad del centro de masas del sistema? b) Después del choque, el muelle se comprime hasta un valor máximo ∆x. ¿Cuál es el valor de ∆x? c) Los bloques eventualmente se separan de nuevo. ¿Cuáles son las velocidades finales de los dos bloques medidas en el sistema de referencia de la mesa? Sol. a) v = 5 m/s; b) ∆x = 0,25 m; c) v’ 1 = 0 m/s, v’ 2 = 7 m/s 10 m/s m1 9. Choques k = 1120 N/m N 67 3 m/s m2 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 9.13) El péndulo cónico de la figura de masa m1 = 10 kg y longitud 1 metro, gira en un círculo horizontal. Al aumentar la velocidad angular choca frontalmente con una bola de masa m2 = 4 kg que está en reposo a 0,5 metros de O. Calcular: a) La velocidad angular en r.p.m. para que choque. b) La velocidad con que sale despedida m2 después del choque. c) La posición y velocidad al cabo de 3 segundos. Sol. a) ω = 32,12 r.p.m.; b) v = 29,5 m/s 1m 0,5 m α O m1 m2 9.14) Se dispara una bala de 20 g de masa y una velocidad inicial de 600 m/s, sobre un bloque de 900 g de masa suspendido como muestra la figura. La bala choca contra el blanco y lo atraviesa completamente. La velocidad con que emerge la bala es igual a la mitad de su velocidad inicial. Calcular la altura alcanzada por el bloque por efecto del impacto. Sol. h = 2,27 m h m1 m2 v0 9. Choques 0,5v0 68 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 10. HIDROSTÁTICA FORMULARIO p − p0 = ρ g z Ecuación fundamental de la hidrostática : Unidades de presión : Pascal Pr esión atmosférica : 1 Pa = pa = 1,013 × 10 5 N m − 2 bar = 10 N m 5 Fuerza contra un dique 1N 1 m2 F= 2 1 atm ≈ 1 bar = 1.000 milibares 1 ρgLH2 2 M = Momento de esta fuerza respecto a un eje 10. Hidrostática (atmósfera) 69 1 ρ g LH3 6 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 10.1) Un depósito que contiene aceite de densidad relativa 0,80 pesa 160 Kp al colocarlo sobre una báscula. Se sumerge en el aceite colgado de un hilo, un cubo de aluminio, de densidad relativa 2,7 de 20 cm de arista. Hallar: a) La tensión en el hilo, b) La lectura que indicaría la báscula. Sol. a) 15,2 Kp b) 166,4 Kp. 10.2) Para sumergir totalmente en T agua y luego en aceite un bloque de madera, se necesita aplicar fuerzas hacia abajo de 21 y 7 Kp E respectivamente. Si el volumen del bloque es de 85 dm3, hallar la densidad relativa del aceite. Sol. 0,835. 10.3) Hallar la aceleración del movimiento de una bola de hierro de densidad relativa 7,8 a) al caer por su propio peso en agua, b) al elevarse cuando se la sumerge en mercurio de densidad relativa 13,5. Sol. a) 8,54 m/s2 b) 7,16 m/s2. 10.4) Una pieza de aleación de magnesio pesa 0,50 Kp en aire; 0,30 Kp en agua y 0,32 Kp en benceno. Calcular la densidad relativa de la aleación y del benceno. Sol. 2,5; 0,9. 10.5) Un cuerpo pesa 10 Kp en el aire y 6 Kp en un líquido cuya densidad relativa vale 0,8. Hallar la densidad relativa del cuerpo. Sol. 2. 10.6) La pared plana de una vasija tiene una inclinación de α = 60º sobre la horizontal. En ella hay un orificio circular de 8 cm de diámetro tapado con un corcho. Desde el centro del orificio hasta la superficie libre del líquido, midiendo por la línea de máxima pendiente de la pared hay l = 1,6 m. El líquido tiene una densidad de 0,95 g/cm3. Calcular la fuerza que soporta el corcho. Sol. 64,8 N. 10.7) Un cuerpo cae desde una altura h = 10 m sobre la superficie de un depósito de agua de h' = 17,5 m de profundidad. Tarda en llegar al fondo desde que entra en el agua t = 1 s. Calcular la densidad del cuerpo. Se desprecia la influencia del aire en el movimiento y la resistencia del agua al mismo. Sol. 3,5. 10. Hidrostática 70 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 10.8) Pesando un cilindro de R = 2 cm de radio y h = 2 cm de altura, en el aire, con pesas de latón, de densidad ρ = 8,4 g/cm3, se obtiene Ma = 192 g. ¿Cual es la masa en el vacío? La densidad del aire es ρ0= 1,293 kg/m3. Sol. 192,0029 g. 10.9) Una pieza de determinada aleación pesa 50 kp en el aire y 45 kp cuando se sumerge en agua. Hallar el volumen V de la pieza y la densidad relativa de la aleación. Sol. 0,005 m3; 10. 10.10) Un cuerpo pesa en el aire 7 g; sumergido en el agua 4,5 g, y en el petróleo 4,9 g. ¿Cuales son las densidades del cuerpo y del petróleo? Sol. 2,8 g/cm3 la del cuerpo; 0,84 g/cm3 la del petróleo. 10.11) Un submarino tiene una masa total de 2,20x106 kg, incluyendo la tripulación y su equipo. El submarino está formado por dos partes, la coraza de presión, que tiene un volumen de 2,00x103 m3, y los tanques de lastre, cuyo volumen es de 4,00x102 m3. Cuando el submarino avanza sobre la superficie del océano, los tanques de lastre se llenan de aire. Cuando el submarino avanza bajo la superficie los tanques de lastre se llenan de agua de mar. a) ¿Qué fracción del submarino queda sobre la superficie cuando los tanques están llenos de aire? La densidad del agua de mar es 1,03x103 kg/m3. b) ¿Qué cantidad de agua de mar debe entrar en los tanques para que el submarino se pueda sumergir hasta una profundidad fija bajo la superficie, es decir, para lograr una flotación neutra? (No tomar en cuenta la masa de aire que queda en los tanques). Sol. a) 0,11; b) V = 264,08 m3 de agua de mar. 10. Hidrostática 71 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 10.12) Una viga AB de longitud 10 metros y peso 1.000 kg, gira alrededor de A y está sujeta por el extremo B, por medio de un cable, a la masa m. Calcular: a) El valor de la masa m introducida en un recipiente con agua para que la viga esté en equilibrio según las condiciones de la figura. b) El valor de la reacción en A. Datos: Densidad del cuerpo: 3 g/cm3 Densidad del agua: 1 g/cm3 Sol. a) m = 1.899 kg; b) R = 17.094 N B 10º 30º 30º A m 10.13) Un cuerpo de densidad relativa ρ = 2 cae desde una altura h1 = 10 M sobre la superficie de un depósito de agua de h2 = 20 m de profundidad. Calcular el tiempo que tarda en llegar al fondo desde que entra en el agua. Se desprecia la resistencia del aire y la del agua. Sol. t = 1,18 s 10. Hidrostática 72 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 10.14) Hallar la aceleración de B y la tensión de la cuerda que tira del cuerpo A mientras este se mueve dentro del agua. MA = 2 kg, MB =10 kg, MPolea= 4 kg, ρA= 2ρagua. Cuando salga del agua, ¿aumentará o disminuirá dicha tensión? Sol. a=(mB - mA)g / 2(mA + mB +MP / 2), T2 aumenta. B µ=0 30º Agua 10. Hidrostática A 73 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería 11. HIDRODINÁMICA FORMULARIO Ley de continuidad : Ecuación de Bernouilli : Teorema de Torricelli : Gasto teórico : 10. Hidrodinámica v1 A1 = v 2 A2 h1 + 1 2 p1 1 2 p2 v1 + ± W 0 = h2 + v2 + + hf 2g γ 2g γ v= 2gh G = Av 74 Torrelavega Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 11.1) El agua sale continuamente del depósito representado en la figura. La altura del punto 1 es 12 m, la del punto 2 y 3 1,2 m. La sección transversal en el punto 2 es 450 cm2 y en el punto 3 es 225 cm2. El área del depósito es muy grande comparada con las secciones del tubo. Calcular: a) la presión absoluta en el punto 2; b) el gasto en litros por segundo. Sol. a) 811 gr/cm2, b) 327 l/s. 1 2 3 11.2) En la figura se representa una instalación para transportar desde 1 hasta 2, una disolución salina cuya densidad es 1,1 g/cm3. Los depósitos son de sección circular. La pérdida de carga debida al frotamiento es de 5 m de altura de líquido. Se pretende determinar la potencia de la bomba 3, en C.V. para que el trasvase de 7,2 m3 de líquido contenidos en 1 se efectúe en una hora. El rendimiento de la bomba es del 60 % Sol. 1,12 C.V. 2mO 2 5mO 1 20 m 2m 3 10. Hidrodinámica 75 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 11.3) El agua que sale de un depósito pasa a una turbina situada 100 m por debajo. El rendimiento es el 80% y recibe 2,7 m3 de agua por minuto. Despreciando el rozamiento en el tubo, calcular la potencia de la turbina, expresada en C.V. y kw. Sol. 48 C.V.; 35 kw. 11.4) Un depósito cerrado que se mantiene parcialmente lleno de petróleo (peso específico 0,9 kg/dm3) tiene una presión en la cámara de gas que está sobre el líquido de 0,7 kg./cm2. Suponiendo que el petróleo salga por una manguera a razón de 150 l/min. , hállese la presión estática delante de la boquilla de salida que está situada 4 m más baja que la superficie del petróleo en el depósito y tiene una entrada cilíndrica de 25 mm (diámetro interior). Supóngase que el rozamiento total en la tubería asciende a 305 mm de altura de petróleo. Sol. 0,9131 kg./cm2. 11.5) Un depósito de gran sección cerrado contiene agua y sobre ella aire comprimido ejerciendo una presión de 5 atmósferas. A una distancia vertical de 2 m bajo la superficie del líquido hay practicado un orificio circular de 0,4 cm de diámetro, situado a 1 m sobre el suelo. Calcular: 1) Velocidad de salida del agua. 2) El gasto teórico y práctico. 3) El alcance horizontal de la vena líquida. 4) La velocidad del líquido al llegar al suelo. 5) El ángulo que forma tal velocidad con la horizontal. Sol. 1) 28,7 m/s; 2) 360 cm3/s, 220 cm3/s; 3) 13 m; 4) 29 m/s; 5) 8º 46’. 11.6) Calcular la velocidad teórica de salida de la vena de agua que fluye por un orificio, a 8 m por debajo de la superficie libre del líquido en un depósito de gran capacidad, sabiendo que en la citada superficie se ejerce una presión 1,5 kp/cm2. Sol. 21,23 m/s. 11.7) Agua de mar (de densidad 1,083 g/cm3) alcanza en un depósito una altura de 1,2 m. El depósito contiene aire comprimido a la presión manométrica de 72 g/cm2. El tubo horizontal de desagüe tiene una sección de 9 cm2. ¿Que cantidad de agua sale por segundo? Sol. 5,436 l/s. 10. Hidrodinámica 76 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega 11.8) Una ciudad se suministra de agua captándola de un lago próximo de donde se eleva a los depósitos situados en lo alto de una colina. La toma se efectúa a 3 m por debajo de la superficie, y el nivel de agua en los depósitos se puede considerar siempre constante y está a 95 m sobre la bomba. La pérdida de carga por frotamiento es de 42,5 kgm/kg de agua para los 1.830 m de tubería de 20 cm, que es la longitud total de la línea, incluidos las longitudes equivalentes de los accesorios. La capacidad de la bomba es de 2.400 l/h; el rendimiento energético del grupo motor-bomba es de 85%. Calcular el costo horario de bombeo, supuesto que la energía eléctrica se pague a 0,45 pts/kw.h. Sol. 0,49 pts/h. 11.9) En determinado punto de una tubería horizontal, la presión manométrica es 5 0,5x10 Pa. En otro punto, la presión manométrica es 0,3x105 Pa. Si las áreas del tubo en estos dos puntos son 20 cm2 y 10 cm2 respectivamente, calcúlese el número de metros cúbicos de agua por minuto que circulan a través de cualquier sección del tubo. Sol. 0,438 m3/min. 11.10) El área de la sección transversal de una tubería horizontal por la que circula agua es de 10 cm2. En una sección, el área de la sección transversal es de 5 cm2. La diferencia de presiones entre ambas secciones es 300 Pa. ¿Cuantos metros cúbicos de agua saldrán de la tubería en 1 minuto? Sol. 0,02683 m3/min. 11.11) Se tiene que suministrar un caudal de Q = 1 m3/s a un depósito de sección muy grande, por medio de una tubería de D = 0,5 m de diámetro, que extrae agua de un lago situado a H = 50 m, por debajo del nivel del agua en el depósito. Para ello se coloca una bomba que impulsa el agua a través de la tubería cuya sección es constante y tiene L = 1.000 m de longitud. Las pérdidas a través de la tubería se expresan por 0,03L.v2/D.2g. Determinar: a) La altura manométrica, W, que debe vencer la bomba. b) La potencia de la bomba si su rendimiento es del 75 %. c) Porcentaje de potencia absorbida por las pérdidas. d) Presión, Pe a la entrada de la bomba, sabiendo que está colocada al nivel de la superficie del lago, siendo la presión atmosférica sobre dicha superficie de 1 kp/cm2. Sol. a) 130,73 m; b) 2.324 C.V.; c) 60,75 %; d) 0,8678 kp/cm2. 10. Hidrodinámica 77 Escuela Universitaria de Ingenieros Técnicos de Minas Fundamentos Físicos de la Ingeniería Torrelavega INDICE Página 1) ECUACIONES DE DIMENSIONES .................. 1 2) CALCULO VECTORIAL .................................. 3 3) CINEMÁTICA................................................. 7 4) ESTÁTICA....................................................13 5) DINÁMICA....................................................27 6) TRABAJO.....................................................39 7) DINÁMICA DE ROTACIÓN.............................44 8) ELASTICIDAD...............................................57 9) CHOQUES ...................................................64 10) HIDROSTÁTICA..........................................69 11) HIDRODINÁMICA .......................................74 Índice