C1-Teoria de circuit..
Anuncio

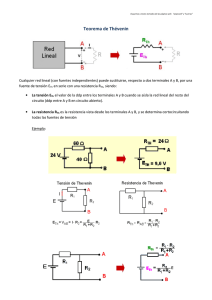
CAPITULO 1 TEOREMAS DE CIRCUITOS ELECTRICOS APLICADA A LA ELECTRONICA ANALÓGICA (3 Hrs) Objetivo: El alumno repasara los conceptos básicos de circuitos eléctricos: fuentes de voltaje, de corriente, dependientes e independientes, reales e ideales así como los teoremas de Thevenin, Norton, Superposición y Máxima transferencia de Potencia, aplicados a la electrónica analógica 1.1 Materiales Eléctricos………………………………(2 Hrs) 1.1.1 Propiedades Eléctricas de los electrones. (También dependen de la temperatura) a) Carga Eléctrica (q)- Un electrón es considerado una partícula atómica donde está contenida la carga eléctrica fundamental que se considera es de polaridad negativa y cuya magnitud se especifica por 1.6 X 10-19 Coulombios (C), esta carga es la responsable de la interacción atómica (reacción química) entre diferentes átomos. La carga Positiva se considera está en el núcleo atómico; en los protones los cuales tienen la misma magnitud de carga que los electrones pero con signo positivo. La carga eléctrica tiene unas reglas de operación: cargas de igual signo se repelen o rechazan. cargas de signos contrarios se atraen. Las fuerzas de atracción y o repulsión de las cargas son función de la magnitud de la carga y de la distancia entre las mismas. La fuerza resultante (F) entre cargas es directamente proporcional a la magnitud de las cargas (q1, q2, qn) en cuestión e inversamente proporcional su distancia. Ley de Coulomb: F 9 109 n m 2 q1 q2 C2 r2 Donde: F en Newton (N) si q1 y q2 están en coulomb (C) r en metros (m) Página b) Símbolo. e− c) Portador de carga. Al electrón se le considera la partícula atómica por excelencia capaz de portar carga eléctrica (llevar, transportar), esta propiedad es la más importante para la electricidad y la electrónica ya que permite el flujo de energía eléctrica entre los sistemas. Al movimiento de electrones de manera ordenada se le denomina corriente eléctrica. 1 Por lo que podemos concluir que la fuerza eléctrica de atracción resultante entre electrones y protones es muy intensa de la misma manera que la fuerza de rechazo entre los protones del núcleo es todavía mas intensa y la explicación que se da nos da para que esas partículas no se junten (electrones con protones) o se separen (protones con protones ó electrones con electrones) es que las fuerzas nucleares son las encargadas de mantener un equilibrio a semejanza de un sistema planetarios. Distancia promedio entre el electrón y el protón es de 5.3 x·10-11 m Distancia promedio entre protones es de 2 x·10-15m d) Masa del electrón. Como toda partícula atómica el electrón también tiene masa, esta es muy pequeña y colabora con la propiedad anterior, su masa es de 9.11×10-31 kilogramos, unas 1800 veces menor que la de los neutrones y protones e) Tamaño del electrón. Radio clásico del electrón, con un valor de 2.8179 × 10−15 m. La electricidad se considera como el flujo de electrones a través de materiales que: permiten su paso fácilmente (conductores), se oponen a su paso (aislantes o dieléctricos) y están entre los dos anteriores (semiconductores) (también se le llama energía eléctrica). La propiedad eléctrica más importante de los materiales es la que expresa que tan fácilmente permiten el paso de la corriente eléctrica: la más común se llama “Resistencia eléctrica (R)” R expresa la oposición que tiene un material al paso de una corriente eléctrica, sus unidades están en ohms ( ) volt Ampere . El mejor material conductor de electricidad sería aquel cuya R=0 Ω (ohm), dicho material no se conoce. Una propiedad que seria la opuesta a la Resistencia eléctrica sería la Conductividad Eléctrica, la cual también expresa que tan buen conductor eléctrico es un material. Se representa con (G) 1 R volt Ampere Siemens S 1.1.2 Conductores y resistores. Permiten el paso de los electrones de manera fácil, típicamente son metales que disponen de muchos portadores de carga (electrones libres, es decir que no tienen fuerzas que los detengan). Sin embargo todos los materiales conductores se oponen al paso de la corriente eléctrica y por consiguiente presentan resistencia eléctrica. A la forma geométrica del material conductor que presenta oposición a la corriente eléctrica se le llama RESISTOR y este dispositivo es muy útil porque nos permitirá controlar a la corriente y al voltaje en un circuito eléctrico Página La resistividad (ρ) que presenta cualquier material es función o depende de la temperatura., dicho coeficiente puede ser positivo PTC, (Positive Temperature Coefficient) o negativo NTC (Negative Temperature Coefficient). 2 La resistencia eléctrica que presenta un resistor es función del material con el que esta hecho el resistor así como la geometría (forma) del resistor, por ejemplo para un resistor de forma cilíndrica, la resistencia que presenta este resistor será: R=ρ(L/S) L = longitud (m) S = área (m2) ρ = resistividad del material con que está hecha el Reistor (Ω-m) MATERIALES Conductores Semiconductores Aislantes Sustancia ρ (Ω-m) Resistividad (α) (1/°K) Coeficiente de temperatura Plata 1.59·10-8 3.8·10-3 Cobre 1.67·10-8 3.9·10-3 Oro 2.35·10-8 3.4·10-3 Aluminio 2.65·10-8 3.9·10-3 Wolframio 5.65·10-8 4.5·10-3 Níquel 6.84·10-8 6.0·10-3 Hierro 9.71·10-8 5·10-3 Platino 10.6·10-8 3.93·10-3 Plomo 20.65·10-8 4.3·10-3 Silicio 4300 -7.5·10-2 Germanio 0.46 -4.8·10-2 Vidrio 1010- 1014 Cuarzo 7.5·1017 Azufre 1015 Teflón 1013 Caucho 1013 - 1016 Madera 108 - 1011 Diamante 1011 Resistividad de algunos materiales a 20 °C En los conductores, aumenta con la temperatura, pudiéndose considerar que para pequeños intervalos de temperatura una dependencia lineal: ρ= ρ20(1 +α(t- 20 °C )) ρ = resistividad de material (Ω-m) ρ20 = Resistividad del material a 20 °C α = coeficiente de temperatura t = temperatura en °C Página Aislantes. Contrario a los conductores presentan una gran oposición al flujo de electrones es decir alta resistividad y permiten que en conjunto con los 3 Los resistores son dispositivos que se usan para manipular corrientes y voltajes en los circuitos eléctricos las más comunes tienen un código de colores que permite identificar su valor de resistencia y de tolerancia. conductores sean los materiales necesarios para poder generar, transmitir, distribuir y usar la energía eléctrica. Su propiedad más importante es la “Rigidez dieléctrica” que expresa el máximo voltaje que puede aplicarse a un aislante antes de que falle (se perfora o destruye eléctricamente) sus unidades son Kv/mm (KiloVolts/milímetros). También se les llama dieléctricos y este término se usa mucho en la tecnología de los capacitores ya que ellos están constituidos por un arreglo especial de conductores y aislantes=dieléctricos. 1.2 Fuentes de Voltaje y Corriente…………………...(1 Hrs) Son dispositivos o artefactos capaces de proporcionar voltaje y/o corrientes eléctricas a elementos que las consumirán, generalmente son artefactos que transforman energía de cualquier tipo a energía eléctrica (mecánicaeléctrica, químicaeléctrica, etc.). Figura 1.1 Fuente de voltaje y/o corriente o fuente de alimentación 1.2.1 Reales e ideales Desde el punto de vista de su funcionamiento sabemos que todos los dispositivos pueden ser analizados como ideales, lo cual facilita su análisis y es una técnica muy usada, pero también suelen analizarse de manera Real es decir con sus limitaciones, este análisis permite encontrar maneras de corregir o mejorar esas limitaciones y nos sirve para explicar el diverso funcionamiento de un dispositivo “Ideal” en el mundo “Real” Página 4 Esta diferencia entre los dispositivos Ideales y Reales nos lleva al concepto de “Modelo” que sería una forma de expresar el funcionamiento de un dispositivo desde un punto de vista diferente. Figura 1.2 Diferentes modelos para diversos dispositivos eléctricos Dispositivo Ideal Presenta un voltaje en sus Fuente de Voltaje, de tensión, terminales que no cambia sin generador importar el tipo de carga que alimente Proporciona la corriente Fuente de Corriente, de deseada a cualquier tipo de intensidad carga sin importar la magnitud de la carga Real El voltaje en sus terminales es función de la carga a alimentar, típicamente se reduce si la carga aumenta y viceversa La corriente proporcionada a la carga es función de la propia carga y no solo de la fuente de corriente Fuente de tensión ideal Es una fuente de tensión que produce una tensión de salida constante, es una Fuente de Tensión con Resistencia interna cero. Toda la tensión va a la carga RL. Página Fuente de tensión real Algunos ejemplos de fuentes de tensión reales son: 5 Figura 1.3 Fuente de tensión o voltaje ideal. Figura 1.4 Fuentes de tensión reales. Son las fuentes de tensión (figura 1.5) que tenemos en la realidad, como ya hemos dicho no existe una fuente ideal de tensión, ninguna fuente real de tensión puede producir una corriente infinita, ya que en toda fuente real tiene cierta resistencia interna. Figura 1.5 Diagrama eléctrico de una fuente de tensión Real Veamos que ocurre en 2 casos, cuando RL vale 10 Ω y cuando vale 5 Ω. Figura 1.6 Efecto de la Resistencia Interna en una carga RL=10Ω Figura 1.7 Efecto de la Resistencia Interna en una carga RL=5Ω Figura 1.8 Comparación de fuente real e ideal. Página 6 Ahora la tensión en la carga no es horizontal, esto es, no es ideal como en el caso anterior. Fuente de tensión (aproximadamente) constante Para que una fuente de tensión sea considerada como una "Fuente de tensión constante" figura 1.9, se tiene que cumplir que la resistencia interna de la fuente (Rint) no este, esto es que sea despreciable. Para que despreciemos la Rint se tiene que cumplir: Figura 1.9 Fuente de tensión aproximadamente constante Solo se pierde el 1 % en el peor caso, por lo tanto se está aproximando a la fuente de tensión ideal. Figura 1.10 Fuente de tensión constante Veamos que ocurre en 2 valores diferentes de RL. Figura 1.11 Efecto de RL en la fuente Resumen Fuente de tensión ideal es la que tiene una Rint= 0 Ω y produce en la salida una VL=constante. Fuente de tensión real es la que tiene una determinada Rint. En esta Rint. hay una pérdida de tensión. El resto de tensión va a la carga que es la que se aprovecha. Fuente de tensión constante es la que tiene una Rint<= RL/100. La caída en la Rint. es como mucho el 1 %, aproximadamente a la ideal, que es el 0 %. Si tenemos que comparar dos fuentes de tensión, la mejor será la que tenga una R int. más pequeña (o sea la que más parecida a la ideal, que tiene una Rint=0 Ω). Página Fuente de corriente ideal (figura 1.12) No existe, es ideal como en el anterior caso de la fuente de tensión ideal 7 Fuentes de corriente En el caso anterior de la fuente de tensión había una resistencia interna muy pequeña, pero una fuente de corriente es diferente, tiene una resistencia interna muy grande, así una fuente de corriente produce una corriente de salida que no depende del valor de la resistencia de carga. Figura 1.12 Fuente de corriente Ideal Fuente de corriente real Son las fuentes que existen en la realidad (figura 1.13). Figura 1.13 Fuente corriente Real Veamos que ocurre con los diferentes valores de RL. Figura 1.14 Efecto de RL en la fuente de corriente Con esto vemos que una fuente de corriente funciona mejor cuando su resistencia interna es muy alta, mientras que una fuente de tensión funciona mejor cuando su resistencia interna es muy baja. La intensidad de carga tiene esta forma: Página Fuente de corriente (aproximadamente) constante 8 Figura 1.15 Comparación entre Fuente de corriente Real e Ideal Figura 1.16 Fuente de corriente aproximadamente constante. Solo se pierde el 1 % en el peor caso. Con esto nos aproximamos a la fuente de corriente ideal. Veamos 2 valores diferentes de RL. Figura 1.17 Efecto de RL en la Fuente de Corriente. Resumen Fuente de corriente ideal es la que tiene una Rint=∞ y produce en la salida una IL=constante. Fuente de corriente real es la que tiene una determinada Rint. En esta hay pérdida de corriente. El resto de la corriente va a la carga que es la que se aprovecha. Fuente de corriente constante es la que tiene una Rint >= 100RL. La corriente que se pierde por la Rint es como mucho el 1 %, aproximadamente a la ideal, que es el 0 %. Si tenemos que comparar 2 fuentes de corriente, la mejor será la que tenga una Rint más grande (o sea la más parecida a la ideal, que tiene una Rint = ∞). Dependientes e independientes Independiente: la salida es independiente del resto del circuito. Dependiente o controlada: la salida se determina o controla mediante un voltaje o corriente existente en otra parte del circuito. Son de gran utilidad para modelar dispositivos físicos tales como amplificadores operacionales y transistores. SÍMBOLOS Fuente de VOLTAJE CORRIENTE Independiente Tabla 1.2 Símbolos de diferentes fuentes de voltaje y corriente Página Dependiente de corriente 9 Dependiente de voltaje Observaciones: La tabla 1.2 muestra los símbolos de las fuentes de continua. Para las fuentes de alterna, a los círculos y rombos, agregar el símbolo ~. Sobre los parámetros de las fuentes dependientes: µ es un parámetro adimensional denominado factor de amplificación de la fuente de voltaje dependiente de voltaje; r es un parámetro en unidades de ohms en la fuente de voltaje dependiente de corriente; g es un parámetro en unidades de siemens en la fuente de corriente dependiente de voltaje; y ß es la ganancia de corriente de la fuente de corriente dependiente de corriente. Teoremas de Circuitos Eléctricos………………(3 Hrs) Teorema de Thevenin Cualquier circuito, por complejo que sea, visto desde dos terminales concretos, es equivalente a un generador ideal de tensión en serie con una resistencia, tales que: La fuerza electromotriz del generador es igual a la diferencia de potencial que se mide en circuito abierto en dichos terminales La resistencia es la que se "ve" HACIA el circuito desde los terminales en cuestión, cortocircuitando los generadores de tensión y dejando en circuito abierto los de corriente Para aplicar el teorema de Thevenin, por ejemplo, en el caso de la Figura 1.18, elegimos los puntos X e Y y, suponemos que desconectamos todo lo que tenemos a la derecha de dichos puntos, (es decir, estamos suponiendo que las resistencias R3 y R4, las hemos desconectado físicamente del circuito original) y miramos atrás, hacia la izquierda. Figura 1.18 En esta nueva situación calculamos la tensión entre estos dos puntos (X,Y) que llamaremos la tensión equivalente Thevenin (Vth) que coincide con la tensión en bornes de la resistencia R2 y cuyo valor es: El siguiente paso es, estando nosotros situados en los puntos indicados (X Y) mirar hacia la izquierda otra vez y calcular la resistencia que vemos, pero teniendo en cuenta que debemos suponer que los generadores de tensión son unos cortocircuitos y los generados de corriente son circuitos abiertos, en el caso de nuestro circuito original, sólo hay un generador de tensión que, para el cálculo que debemos hacer lo supondremos en cortocircuito y ¿que es lo que vemos? Página Por lo que la resistencia equivalente Thevenin, también llamada impedancia equivalente, Zth vale: 10 Pues si observamos la figura 1.18, lo que vemos es que, las resistencias R1 y R2 están en paralelo. Teorema de Norton Cualquier circuito, por complejo que sea, visto desde dos terminales concretos, es equivalente a un generador ideal de corriente en paralelo con una resistencia, tales que: La corriente del generador es la que se mide en el cortocircuito entre los terminales en cuestión. La resistencia es la que se "ve" HACIA el circuito desde dichos terminales, cortocircuitando los generadores de tensión y dejando en circuito abierto los de corriente.-( Coincide con la resistencia equivalente Thévenin) Aplicando el Teorema de Norton al circuito de la figura 1.18, nos quedará el siguiente circuito: Donde hemos cortocircuitado los puntos X Y de la figura 1.18. La corriente que circula por entre estos dos puntos la llamaremos Ith y lógicamente es igual a la tensión V del generador de tensión dividido por la resistencia R1 (Ley de OHM) la resistencia Thevenin es la misma que la calculada anteriormente, que era el paralelo de R1 y R2. EQUIVALENCIA ENTRE THEVENIN Y NORTON dos o más fuentes independientes, cualquier voltaje o corriente del circuito puede calcularse como la Página Teorema de Superposición El teorema de superposición dice formalmente que: En cualquier circuito resistivo lineal que contenga 11 Sea cual sea el equivalente obtenido es muy fácil pasar al otro equivalente sin más que aplicar el teorema correspondiente, así por ejemplo, supongamos que hemos calculado el equivalente Thévenin de un circuito y hemos obtenido el circuito de la izquierda de la figura siguiente: Aplicando el teorema de Norton a la figura de la izquierda, cortocircuitaremos la salida y calcularemos la corriente que pasa entre ellos que será la corriente :Ith= 10/20 = 0,5 A.y la resistencia Norton es 20 Ω por lo que nos quedará el circuito equivalente Norton de la derecha suma algebraica de todos los voltajes o corrientes individuales originados por cada fuente independiente actuando por sí sola, es decir, con todas las demás fuentes independientes eliminadas. Hasta ahora todos los circuitos que se han manejado son lineales, por lo tanto este teorema puede ser aplicado a cualquier circuito anteriormente explicado. Se puede decir que linealidad y superposición son conceptos que significan lo mismo; solo que linealidad es un concepto más matemático y superposición es mas físico. Normalmente se define superposición como: "La respuesta de un sistema lineal a varios estímulos es la suma de las respuestas a cada uno de los estímulos". Esto se puede ver más claro con el siguiente diagrama de bloques: En la parte (a) de la figura, se tiene un sistema lineal al que se le aplican dos estímulos diferentes (E1 y E2) y se obtiene una respuesta (R1), el resultado seria de la forma: R1 f1 ( E1 ) f 2 ( E2 ) Donde f1(E1) y f2(E2) son funciones lineales de E1 y E2 respectivamente, en la parte (b) se tiene el mismo sistema lineal pero aplicando otro dos estímulos (Ea y Eb) y se obtiene como resultado una respuesta (R2) , de la forma: R2 f1 ( Ea ) f 2 ( Eb ) La respuesta total (R) del sistema lineal seria de la forma: R R1 R2 f1 ( E1 Ea ) f 2 ( E2 Eb ) Es de notar que para sumar dos estímulos estos deben tener las mismas características y ser del mismo tipo. Este concepto se aplica a los circuitos eléctricos, por medio del teorema de superposición. Ejemplo: En este circuito se tiene dos fuentes independientes de voltaje (V1 y V2) y una red de tres resistencias (R1, R2 y R3), el objetivo del ejercicio es encontrar el valor del voltaje sobre la resistencia R3, el cual se llama VX. Ahora bien, utilizando el principio de superposición de fuentes se realizaría lo siguiente: Como primer paso se analizaría el circuito solo utilizando la fuente V1 y la fuente V2 seria eliminada o igualada a cero (corto-circuito) como en la siguiente figura: Como se observa R3 y R2 se encuentran en paralelo y al mismo valor de voltaje, por lo tanto Vx seria igual al divisor de tensión entre R1 y el paralelo entre R2 y R3, de la siguiente manera: R1 V1 R2 || R3 R2 || R3 Como segundo paso se analizaría el circuito solo utilizando la fuente V2 y la fuente V1 seria eliminada o igualada a cero (corto-circuito) como en la siguiente figura: VX ' ' I X R1 || R3 R2 V1 R1 || R3 R1 || R3 12 R2 || R3 Página VX ' I X Por lo que finalmente: VX VX ' VX ' ' R1 V1 R2 || R3 R2 || R3 R2 V1 R1 || R3 R1 || R3 Teorema de máxima transferencia de potencia Muchas aplicaciones de circuitos requieren que la máxima potencia disponible de una fuente se transfiera a un resistor de carga Rc como ya se sabe un circuito A puede reducirse a su equivalente de Thevenin. El problema general de la transferencia de potencia puede examinarse en términos de la eficiencia y la economía. Los sistemas eléctricos se diseñan para llevar la potencia a la carga con la mayor eficiencia, al reducir las pérdidas en las líneas de potencia. Por ello, el esfuerzo se centra en reducir RTH que representaría la resistencia de la fuente más la de la línea. Por eso resulta atractiva la idea de usar líneas superconductoras que no ofrezcan resistencia para transmitir potencia. El circuito A es un circuito que contiene resistencias, fuentes independientes, fuentes dependientes. La resistencia Rc representa la carga. Un equivalente Thevenin sustituye al circuito A. Donde Vf(t) es la fuente de tensión de Thevenin. Por lo tanto tendremos: Ecuación p(t ) i (t ) i (t ) p(t ) 2 Análisis de Unidades ( w) ( A2 ) ( ) RC v f (t ) RC ( A) RTH v f (t ) RC RTH 2 ( w) RC (v ) ( ) (v ) 2 ( )2 (v ) 2 ( ) Suponiendo que vf(t) y RTH son constantes para una fuente dada, la potencia máxima será función de Rc. Para calcular el valor de Rc que maximiza la potencia, se usa el cálculo diferencial para determinar el valor de Rc para el que la derivada es igual a cero. v f (t ) dp dRC RC RTH 2 RC 2 dp (v f (t )) RC dRC ( RC RTH ) 2 u v Ecuación. 2.1 (RC RTH ) 2 , dv 2(RC RTH ) y du (v f (t ))2 Página u dv v du v2 Si hacemos: u (v f (t ))2 RC , v d 13 Aplicando la fórmula para el tipo de derivada Para encontrar el máximo ó el mínimo de la función se iguala a cero y sustituimos los valores de u, v, du y dv en la Ecuación 2.1 d u v ((v f (t ))2 RC ) (2( RC RTH )) ((RC ((RC RTH ) 2 ) ((v f (t ))2 ) RTH ) 2 ) 2 0 Reduciendo la ecuación para encontrar la condición donde la derivada se hace cero ((RC ((v f (t ))2 ( RC (2 Rc RC RTH ) ) RTH )) ((2 Rc) ( RC RTH ) 0 RTH )) 2 2 RC La máxima potencia se dará: pmàx (t ) RTH 0 0 RTH )) 0 RC RTH (v f (t ))2 (v f (t ))2 (v f (t ))2 (2RTH ) 2 4RTH 4RC 14 RTH )) ((2 Rc) ( RC Página ((v f (t ))2 ( RC