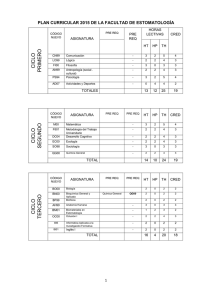
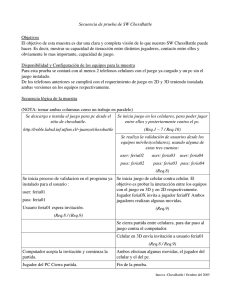
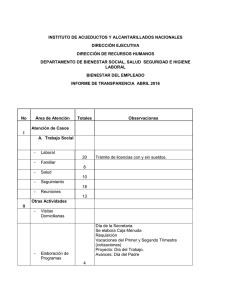
1 1 1 1 1 1 2 10 6 10 R R R R = + → = + ⋅ ⋅ 1,5 10 R = ⋅ Ω 300 V ε

1
1
1
1
1
1
=
+
→
=
+
R4 R2 R3
R4 2 ⋅ 104 6 ⋅104
R4 = 1,5 ⋅10 4 [Ω ]
ε = ε 2 − ε1 = 300[ V ]
R1
ε1
R2
ε2
Req = R1 + R4 = 1⋅ 104 + 1,5 ⋅ 104
R3
C
R1
Req = 2,5 ⋅ 104 [Ω ]
ε
Las diferencias de potencial instantáneas
ε
q
vab =
g
vbc = i ⋅ Req
c
1
2
R4
C
ε1
Req
ε2
C
Usando estas expresiones en la regla de las mallas de
Kirchhoff.
ε − iReq −
q
= 0.
c
(El potencial disminuye en una
cantidad q/c si nos desplazamos de a
a b y en iR si nos movemos de b a c.)
Despejando i tenemos: i =
ε
q
−
(*)
Req ReqC
(A medida que aumenta q el
término q/Rc crece y la carga
del capacitor se aproxima a su
valor final (Qf ) y la corriente
disminuye hasta llegar a cero.)
Entonces cuando i = 0 y q = Q f
Qf
ε
=
Req
Req ⋅ C
Qf = ε ⋅C
(Q
f
no depende de Req )
Qf = 300 ⋅ 4 = 1200 [ µ C]
De (*) tenemos que si i = dq/dt entonces
dq
ε
q
1
=
−
=−
( q − Cε )
dt Req Req ⋅ C
RC
ordenando y cambiando las variables por q’ y t’:
dq ′
−dt ′
=
q − Cε Req ⋅ C
integrando a ambos lados:
q
t
dq ′
dt ′
∫0 q′ − Cε = − ∫0 Req ⋅ C
 q − Cε
ln 
 −Cε
−t

=

 Req ⋅ C
Ahora calculemos los tiempos separadamente si sabemos que
Qf = ε ⋅c:
1

Qf
−
Qf


−t1
ln  3
=

−
Qf

 Req ⋅ C


2
ln   ⋅ Req ⋅ C ⋅ ( −1) = t1
3
t1 = 40.546,51[ µs ]
2

Qf
−
Qf
3

−t 2
ln 
=
 −Qf
 Req ⋅ C


1
ln   ⋅ Req ⋅ C ⋅ ( −1) = t2
3
t2 = 109.861,23[ µs ]
∴ t2 − t1 = 69.314,72 [ µ s]