Fundamentos Físicos I : Campo eléctrico Parcial 2 1.

Fundamentos Físicos I : Campo eléctrico
Parcial 2
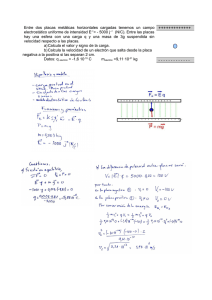
1.-Se colocan paralelamente dos placas metálicas conductoras idénticas, A y B, de
superficie S y espesor h. Las placas tienen cargas q A=4 Q y q B =− 4 Q . Determine:
a) Las densidades superficiales de carga,  1 ,  2 ,  3 y  4 , en las diferentes
caras, (1), (2), (3) y (4), de las láminas conductoras.
b) El campo eléctrico 
E en las diferentes regiones del espacio.
c) La diferencia de potencial entre las láminas conductoras.
Nota: suponer que no hay carga sobre el área lateral de altura h.
a) Consideremos que la placa inferior es la A y la superior la placa B. Como las
placas son medios conductores, desde la perspectiva eléctrica cada placa se asemeja,
con los datos del ejercicio, a un conjunto de dos planos infinitos cargados con unas
densidades superficiales de carga. Los campos eléctricos debidos a los distintos planos
son uniformes y de valor E = σ / ( 2ε 0 ) . Inicialmente voy a suponer que todas las
densidades de carga son positivas para orientar los campos y hallaremos su verdadero
signo a partir de la conservación de la carga. De acuerdo con la figura las densidades
superficiales de carga en los diferentes planos son σ1 en el plano inferior, σ2 en el otro
plano de la placa A, σ3 en el plano inferior de la placa B y σ4 en el plano superior de
dicha placa.
Conservación de la carga: σ 1 + σ 2 = 4Q / S [1.1] y σ 3 + σ 4 = − 4Q / S [1.2]
Los campos eléctricos en los interiores de las placas deben ser nulos. Las
contribuciones a dichos campos, de los diferentes campos eléctricos debidos a los
planos de carga están orientados como sigue:
r
σ r r
σ1 r r
σ r r
σ r
j ; E2 = − 2 j ; E3 = − 3 j ; E4 = − 4 j
Placa A: E1 =
2ε 0
2ε 0
2ε 0
2ε 0
r
σ r r
σ1 r r
σ r r
σ r
j ; E2 = 2 j ; E3 = 3 j ; E4 = − 4 j
Placa B: E1 =
2ε 0
2ε 0
2ε 0
2ε 0
El campo eléctrico en el interior de la placa A es nulo, por tanto σ 1 = σ 2 + σ 3 + σ 4 [1.3]
El campo eléctrico en el interior de la placa A es nulo, por tanto σ 1 + σ 2 + σ 3 = σ 4 [1.4]
Las ecuaciones [1.1], [1.2], [1.3] y [1.4] forman un sistema con 4 incógnitas, que
tiene por solución σ 1 = 0 ; σ 2 = 4Q / S ; σ 3 = − 4Q / S y σ 4 = 0 (C/m2); de lo cual se
deduce que toda la carga de cada una de las placas está localizada sobre los planos más
próximos.
b) Del párrafo anterior se deduce que los campos eléctricos debidos a estos
planos tienen sentidos contrarios y módulo igual fuera de la región situada entre los
planos (2) y (3) por lo que el campo en dichas regiones es nulo, y en cambio entre los
planos (2) y (3) los campos son de igual sentido y módulo por lo que el campo en dicha
zona es 2 veces el valor de uno de ellos. En consecuencia,
r
 E = 0 si y ≤ 0 o y ≥ d
 r
(V/m)
4Q r

E
=
j si 0 < y < d

ε 0S

c) La diferencia de potencial entre las placas conductoras se determina mediante
la circulación del campo eléctrico entre ambas,
ϕ ( 3)
r r
dϕ = − E ⋅ dr ⇒
∫
(3)
dϕ = −
ϕ ( 2)
∫
(2)
4Q r r
4Q
j ⋅ dr = −
ε 0S
ε 0S
∆ ϕ = ϕ ( 2 ) − ϕ ( 3) =
4Qd
ε 0S
d
∫
0
dy = −
4Qd
ε 0S
( V)
2.- Un condensador esférico tiene armaduras de radios Ri = 1.9 mm y Re= 2.0 mm, y un
dieléctrico que ocupa todo el espacio entre ambas, de permitividad relativa εr= 4. El
condensador se carga conectándose a una fuente de tensión φ = 9 V.
a) Determine la capacidad del condensador.
b) Calcule la carga libre en cada armadura.
c) Si se conecta la armadura exterior a Tierra, determine cómo queda cargada
dicha placa.
Vamos a suponer que la placa interna del condensador está conectada al terminal
positivo de la fuente de tensión. La simetría esférica del problema nos dice que los
r
r
campos tienen la dirección radial, D ( r ) = D ( r ) ur siendo r la distancia al centro de las
superficies esféricas que forman el condensador.
La aplicación del teorema de Gauss del desplazamiento sobre una superficie
esférica de radio r con centro en el centro del condensador nos permite hallar D en todo
el espacio y de ese valor podemos calcular el campo eléctrico.
r
r r
r
l
qenc
D ⋅ dS = D P dS =
D ⋅ dS = { D es fijo en SE (r )} = D
dS = D 4π r 2
, SE =
Ñ∫
SE ( r )
{
}
Ñ∫
SE ( r )
Ñ∫
SE ( r )
l
r
qenc
, SE r
D( r) =
ur [2.1]
4π r 2
Si {Q, -Q} son las cargas en las placas del condensador, de [2.1] seducimos
r
l
r < Ri ⇒ qenc
D ( r < Ri ) = 0
, SE = 0 ⇒
r
l
r > Re ⇒ qenc
D ( r > Re ) = 0
, SE = + Q + ( − Q ) = 0 ⇒
r
Q r
l
Ri < r < Re ⇒ qenc
=
+
Q
⇒
D
ur [2.2]
( Ri < r < Re ) =
, SE
4π r 2
A partir del cálculo anterior del desplazamiento eléctrico D hallamos el campo
r r
eléctrico en las diferentes regiones mediante la relación E = D / ε . De dicha expresión
deducimos que el campo eléctrico solo es distinto de cero en la zona entre placas del
r
Q
r
u
condensador, y tiene por valor E ( Ri < r < Re ) =
2 r.
4 π ε 0ε r r
a) Determinamos la diferencia de potencial entre placas, en función de la carga,
y a partir de dicha relación hallamos la capacidad del condensador.
ϕ ( Re )
Re
Re
Re
r
r r
 1 1
Q
ur
Q
Q
r
dϕ = − E ⋅ dr = −
⋅
dr
u
=
=
r
 − 
4π ε 0 ε r r 2
4 π ε 0 ε r r R 4 π ε 0 ε r  Re Ri 
i
∫
ϕ ( Ri )
∫
∫
Ri
Ri
 1 1
 Ri − Re 
Q
Q
 −  =


4 π ε 0 ε r  Re Ri  4 π ε 0 ε r  Ri Re 
 Re − Ri 
Q
ϕ = ϕ ( Ri ) − ϕ ( Re ) =

 [2.3]
4 π ε 0 ε r  Ri Re 
ϕ ( Re ) − ϕ ( Ri ) =
De [2.3] C =
RR
Q
4 1,9 ⋅ 2 ⋅ 10− 6
= 4π ε 0 ε r i e =
= 16.9 pF
ϕ
Re − Ri 9 ⋅ 109 0,1 ⋅ 10− 3
b) La armadura interna tiene una carga positiva y la externa el mismo valor pero
de signo contrario. La carga se halla del valor de la capacidad o de la relación [2.3], y se
obtiene Q = C ϕ = 16,9 ⋅ 9 = 152 pC ; las cargas respectivas son {+152, - 152} pC.
c) Si se conecta la placa exterior a masa no le sucede nada a su carga ya que el
campo eléctrico en el exterior es nulo y la armadura estaba por tanto a potencial nulo,
por tanto Q( Re ) = Q = − 152 pC
c) Si se conecta la placa exterior a masa no le sucede nada a su carga ya que el campo
eléctrico en el exterior es nulo y la armadura estaba por tanto a potencial nulo, por tanto
Q( Re ) = Q = − 152 pC .
3.- La figura muestra las líneas de un campo eléctrico en
una cierta región del espacio y tres electrones localizados
en las posiciones (1), (2) y (3). Responda razonadamente
a las siguientes cuestiones:
a) ¿Sobre qué electrón actúa mayor fuerza?
b) ¿Qué electrón está a mayor potencial?
c) ¿Qué electrón presenta la mayor energía potencial
electrostática?
Datos: Carga del electrón: -1.6x10-19 C
a) El campo eléctrico es uniforme en el espacio
donde están localizados los electrones, como todos están sometidos al mismo valor del
campo y todos ellos tienen la misma carga, todos se encuentran sometidos a la misma
r
r
fuerza F = qe E .
b) El campo eléctrico está orientado de modo que su sentido es el de los
r
r
potenciales decrecientes E = − ∇ ϕ , por lo tanto según la figura el electrón situado más a
la izquierda se encontrará a mayor potencial, y el situado más a la derecha estará a
menor potencial, por lo que ϕ ( 1) > ϕ ( 2 ) > ϕ ( 3) , es decir el electrón (1) está a mayor
potencial.
c) La energía electrostática asociada a una carga inmersa en un campo eléctrico
es U E = q ϕ , y como la carga del electrón es negativa se tiene que a mayor potencial le
corresponde una menor energía electrostática U E ( 1) < U E ( 2 ) < U E ( 3) , por lo que el
electrón (3) presenta la mayor energía electrostática. Alternativamente puede verse del
U , F
 tiene el sentido de U decreciente, y como
 =−∇
siguiente modo: como F
 está dirigida hacia la izquierda, la U decrece en ese sentido.
F
4.- Una esfera metálica de radio R = 0.36 m está cargada de forma que su potencial es
V1 = 1000 V. Mediante un hilo conductor se pone en contacto con otra esfera metálica
que estaba inicialmente descargada y suficientemente alejada de la primera para
despreciar el efecto del campo que creaba ésta. Tras un breve transitorio, se comprueba
que la segunda esfera (o más claramente podríamos decir las dos esferas) adquiere un
potencial de V2 = 300 V. Calcular:
a) La carga en la primera esfera antes de la unión.
b) La carga de las dos esferas tras la unión.
c) El radio de la segunda esfera.
d) Si a continuación se conecta la primera esfera a tierra manteniendo la unión
entre las esferas, ¿cuál es la carga final en cada una de ellas?
a) El potencial de una esfera conductora aislada, es como el creado por una
carga puntual de valor igual a la carga total de la esfera, situada en el centro de la esfera,
kQ
a una distancia igual al radio de dicha esfera. Así ϕ esf , cond = ϕ 0 =
.
R
3
9
De los datos del ejercicio Q = ϕ 0 R / k = V1 R / k = 10 ⋅ 0,36 / ( 9 ⋅ 10 ) = 40 nC
b) Uniendo las esferas se produce un trasvase de carga hasta que se igualen los
potenciales, que se estabiliza a un valor V2 = 300 V. Sean Q1 y Q2 las cargas finales de
las esferas.
De la conservación de la carga obtenemos Q = Q1 + Q2 [4.1]
k Q1 k Q2
=
= V2 = 300 [4.2]
De la igualdad de potenciales
R
R′
k Q1
300 ⋅ 0,36
= 300 ⇒ Q1 =
= 12 nC y de [4.1]
De [4.2]
R
9 ⋅ 109
Q2 = Q − Q1 = 40 − 12 = 28 nC
c) De [4.2]
k Q2
k Q2 9 ⋅ 109 ⋅ 28 ⋅ 10− 9
= 300 ⇒ R′ =
=
= 0,84 m
R′
300
300
d) Al conectar una esfera a Tierra, como están ambas conectadas, es como si
tuviésemos un conductor único conectado a masa así que iría descargándose mientras
existiese campo eléctrico, este iría disminuyendo hasta hacerse cero, instante en el cual
el potencial de las esferas se haría cero, igual al de Tierra. En estas circunstancias las
esferas habrían perdido toda la carga, pues de lo contrario seguiría existiendo campo
eléctrico en el espacio que las rodea y no habrían alcanzado el potencial nulo. Así que
finalmente ambas esferas se descargan por completo: Q1′ = Q2′ = 0 .