ESTRUCTURA ATÓMICA - IES Juan de Aréjula

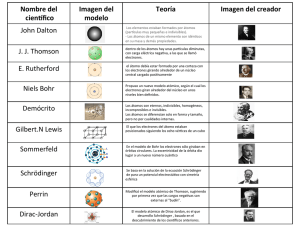
ESTRUCTURA ATÓMICA
ESTRUCTURA ATÓMICA
Contenidos
1.
Modelos atómicos
1.
2.
3.
4.
5.
2.
Niveles:
2º Bachillerato Química
Dalton
Thomson
Rutherford
Bohr
Mecánico cuántico
El Sistema Periódico
1.
2.
Configuración electrónica y periodicidad
Propiedades periódicas
Modelo atómico de Dalton
John Dalton (1766-1844)
Químico y físico británico
1. Los elementos químicos están formados por partículas muy
pequeñas e indivisibles llamadas átomos
2. Todos los átomos de un elemento químico dado son idénticos
en su masa y demás propiedades
3. Los átomos de diferentes elementos químicos son distintos, en
particular sus masas son diferentes
4. Los átomos son indestructibles y retienen su identidad en los
cambios químicos
5. Los compuestos se forman cuando átomos de diferentes
elementos se combinan entre sí, en una relación de números
enteros sencilla, formando entidades definidas (hoy llamadas
moléculas)
6. En las reacciones químicas los átomos simplemente se
redistribuyen.
Símbolo
Elemento
Masa
Hidrógeno
1
Nitrógeno
5
Carbono
6
Oxígeno
8
Representación de un cambio
químico, según Dalton:
+
El descubrimiento del electrón
Fueron los experimentos de Faraday sobre la electrólisis, realizados hacia 1830, los que
sugirieron que los átomos no eran tan simples e indivisibles como Dalton supuso. El hecho
de que la corriente eléctrica produjera un cambio químico indicaba la existencia de una
relación entre electricidad y materia, o en otras palabras, que los átomos debían poseer una
estructura de naturaleza eléctrica.
Un tubo de vacío es un tubo de vidrio equipado con dos placas a modo de electrodos que
pueden conectarse a los dos polos de un generador. Si se encierra en él un gas, no se
observa fenómeno alguno, aunque apliquemos un alto voltaje, ya que los gases son
aislantes casi perfectos en condiciones habituales. Pero al hacer el vacío manteniendo un
voltaje elevado, el gas comienza a conducir la electricidad, fenómeno que va acompañado
de emisión de luz. Si el vacío se intensifica, la luz desaparece. En estas circunstancias
puede verse una débil fluorescencia en la pared del tubo opuesta al cátodo. Como al colocar
cualquier objeto entre los electrodos aparece una sombra, ya los primeros científicos, que
estudiaron estos fenómenos en la segunda mitad del siglo XIX, supusieron que la
fluorescencia era producida por una radiación invisible que salía del cátodo. De ahí el
nombre de rayos catódicos.
El descubrimiento del electrón
Tubo de descargas
William Crookes (1832-1919)
Químico y físico británico
Cátodo
Tubo de Crookes
1875
Gas a baja
presión
El descubrimiento del electrón
Los rayos catódicos
tienen las siguientes
propiedades:
• Están constituidos por partículas con masa.
• Esas partículas viajan en línea recta hasta
el ánodo.
• Las partículas se desvían en campos
eléctricos o magnéticos.
• Sus características no dependen del gas ni
electrodos utilizados.
Ánodo
El descubrimiento del electrón
En 1897, Joseph John Thomson deja claro la
naturaleza de los rayos catódicos
•
Se trata de unas partículas procedentes de los
átomos del cátodo y a las que llama electrones y
de las cuales determina la relación carga/masa
•
Dicha relación no depende del gas ni de los
electrodos usados
J.J. Thomson (1856-1940)
Físico británico
q/m=1,759·1011 C/kg
El descubrimiento del electrón
En
1909 Robert Andrews Millikan
determina la carga eléctrica del
electrón con su famoso experimento
de la gota de aceite
qe =1,602·10-19 C
¡Casi 2000 veces más
pequeña que el menor
de los átomos
(hidrógeno)!
me =1,602·10-19 C/1,759·1011 C/kg=
=9,107·10-31 kg
Robert Andrews Millikan
(1868-1953)
Físico norteamericano
El modelo atómico de Thomson
En 1904 Joseph John Thomson habla de un nuevo modelo
atómico
•
El átomo es como una esfera maciza y uniforme en la
que se encuentra toda la carga positiva.
•
Los electrones se encuentran incrustados en ella
compensando la carga.
•
Los iones negativos se forman al adicionarse más
electrones.
•
Los iones positivos se forman al perderse electrones.
J.J. Thomson (1856-1940)
Físico británico
El descubrimiento del protón
En 1886 Eugen Goldstein descubre los rayos canales, para
ello utilizó un tubo de descarga con el cátodo perforado por
un pequeño orificio o “canal”.
•
•
Mediante estudios sobre su comportamiento en campos
eléctricos y magnéticos se demostró que estos rayos canales
estaban formados por partículas cargadas positivamente y
que eran características del gas encerrado en el tubo de
descarga.
La partícula de menor masa (gas hidrógeno) tenía una carga
igual a la del electrón pero positiva, y una masa unas 2000
veces mayor.
Carga
Masa
Protón
+1,6·10-19C
1,67·10-27kg
Electrón
-1,6·10-19C
9,11·10-31kg
Eugen Goldstein (1850-1931)
Físico alemán
H → H + + 1e −
El modelo atómico de Rutherford
Ernest Rutherford (1871-1937)
Químico y físico británico
Hans Wilhelm Geiger
Ernest Marsden
El modelo atómico de Rutherford
1911
El modelo atómico de Rutherford
En 1911 Ernest Rutherford plantea un modelo
planetario del átomo:
•
El átomo está formado por el núcleo, situado
en su centro, muy pequeño en comparación
con el tamaño del átomo y que contiene toda
la carga positiva y casi toda la masa del
mismo. Contiene todos los protones del átomo
•
Cuenta también con una corteza, donde se
sitúan los electrones, que giran alrededor del
núcleo en órbitas circulares (a modo de
planetas alrededor de su estrella).
•
Existen tantos electrones en la corteza como
protones en el núcleo cuando el átomo no
está ionizado.
•
Los electrones se sitúan muy alejados del
núcleo, de manera que casi todo el espacio
del átomo está vacío
El descubrimiento del neutrón
En 1920 Rutherford sugiere la existencia de un tercer tipo de
partícula, con masa parecida a la del protón y sin carga, a la
que propuso llamarle neutrón y que permitiría explicar los
cálculos realizados sobre la estabilidad del núcleo.
El neutrón fue identificado por primera vez, en 1932 por James
Chadwick estudiando los resultados de los experimentos
realizados por los esposos Joliot-Curie, que habían producido
un tipo de radiación, al producirse la interacción de
partículas alfa con núcleos de berilio.
Carga
Masa
Protón
+1,6·10-19C
1,67·10-27kg
Electrón
-1,6·10-19C
9,11·10-31kg
Neutrón
0
1,67·10-27kg
9
4
Be + 24 He → 126 C + 01n
James Chadwick (1891-1974)
Físico británico
Números atómico y másico
Se define el número atómico (Z) como el número de protones que tiene un átomo.
Expresa pues la carga positiva del mismo.
• Todos los átomos de un mismo
elemento químico tienen el mismo
número atómico.
• Si el átomo es neutro el número
atómico también coincide con el
número de electrones que posee.
• Si se trata de un catión el número de
electrones coincide con el número
atómico menos la carga del ion.
• Si se trata de un anión el número de
electrones coincide con el número
atómico más la carga del ion.
Elemento o ion
Z
A
Nº electrones
Nº protones
Nº neutrones
Na
11
23
11
11
12
Na+
11
23
10
11
12
Cl
17
37
17
17
20
Cl-
17
37
18
17
20
Se define el número másico (A) como el
número
de
protones
y
neutrones
(nucleones) que tiene un átomo en su núcleo.
Expresa pues la casi totalidad de la masa del
mismo.
A = Z + n º neutrones
A
Z
X
• No todos los átomos de un elemento químico tienen porqué tener el mismo número de
neutrones, por tanto su número atómico puede variar.
• El núcleo de un átomo se representa con el símbolo del elemento al que pertenece e
indicando su número atómico como subíndice y su número másico como superíndice.
Isótopos
Se denominan isótopos a aquellos átomos que, perteneciendo al mismo elemento, tienen
diferente número másico, es decir, son aquellos que tienen el mismo número atómico y
difieren en su número másico.
• La mayoría de los elementos están
formados por mezclas isotópicas de
dos o más isótopos.
• La masa atómica de un elemento es la
media ponderada de las masas
atómicas de sus isótopos.
• Las masas de los isótopos son algo
más que pequeñas que sus números
atómicos porque se produce una
pérdida de masa, liberada en forma
de energía, en la formación del núcleo.
Elemento
C
O
Isótopo
Abundancia
Masa atómica
C12
98,93%
12,000000000
C13
1,07%
13,003354000
C14
10-10%
14,003241982
O16
99,757%
15,99491463
O17
0,038%
16,9991312
O18
0,205%
17,9991603
Masa
atómica
12,0107
15,9994
M at = A1M at1 + A2 M at2 + ... + An M atn
M atO = 0,99757·15,99491463u + 0,00038·16,9991312u
+0,00205·17,9991603u = 15,9994u
Un elemento químico es una sustancia pura formada
por átomos que tienen el mismo número atómico.
La radiación del cuerpo negro
• A la radiación emitida por un cuerpo debido a su temperatura
se le denomina radiación térmica.
• Todos los cuerpos emiten radiación térmica y al mismo
tiempo la absorben de otros de sus inmediaciones.
• Cuando se alcanza el equilibrio térmico las velocidades de
emisión y absorción se igualan.
• La materia en estado condensado (sólido y líquido) emiten
radiación de todas las frecuencias del espectro, pero
dependiendo de la temperatura y de la sustancia en sí
emite más en unas frecuencias que en otras.
El hierro emite principalmente
en la frecuencia del rojo cuando
su temperatura es próxima a la
de fusión
• Los cuerpos a temperatura ordinaria se ven por la luz que
reflejan y no por la que emiten, pero a temperaturas altas se
vuelven auto-luminosos.
La radiación del cuerpo negro
• La radiación térmica es mayor cuanto mayor sea la temperatura, además la
frecuencia de emisión más intensa cambia con ésta (Esta relación se utiliza en
los radiotelescopios para medir la temperatura de las estrellas)
• Los cuerpos negros son aquellos que absorben todas las frecuencias de la
radiación térmica que reciben (se ven negros)
• El espectro de emisión depende del cuerpo que emite, pero en los llamados
cuerpos negros no depende del material de que estén hechos
La radiación del cuerpo negro
1900
Resultados obtenidos a partir de las
consideraciones clásicas de emisión
continua de energía (Rayleigh y Jeans)
Resultados obtenidos a partir de las
consideraciones cuánticas de Planck que
supone emisión de cuantos energéticos
donde h = 6.63·10-34 Js es la constante
de
Planck, n es un número entero y ν es la
frecuencia correspondiente al respectivo
modo.
Véase aquí la radiación del cuerpo
negro para distintas temperaturas
Hipótesis de Planck
En 1900 Max Planck formula la primera explicación satisfactoria
del espectro de radiación del cuerpo negro
•
Admite que la materia está formada por un gran número de
partículas que oscilan, emitiendo cada una de ellas energía
en forma de ondas electromagnéticas.
•
Postula que esas partículas no emiten cualquier valor de
energía sino cuantos de la misma de valor hν, donde
h=6,6256·10-34 J·s y ν es la frecuencia de la radiación
emitida
•
El número de osciladores a baja frecuencia es muy superior
al de osciladores a alta frecuencia.
E = h ⋅ν
Cuanto de energía
de frecuencia ν
Constante de Planck
h = 6,6256·10-34 J·s
Max Planck (1858-1947)
Físico alemán
La radiación electromagnética
La radiación electromagnética es una forma de transmisión de energía en
la que campos eléctricos y magnéticos se propagan mediante ondas a
través del espacio vacío o de un medio. Su origen está en la aceleración
de una partícula cargada.
La longitud de onda es la
distancia que separa a un
punto del siguiente que se
encuentra en su mismo
estado de vibración
La radiación electromagnética
• La luz visible es solo una de las muchas formas de radiación electromagnética.
• Las ondas de radio, TV, calor, rayos ultravioletas o rayos X, son también
radiaciones electromagnéticas, que difieren en su longitud de onda.
• Todas estas ondas radian según la teoría electromagnética de Maxwell.
• Las ondas electromagnéticas viajan todas a la misma velocidad. Así, en el vacío su
velocidad es la velocidad de la luz, c=3·108m/s.
• Como en toda onda, se cumple la relación v=λν.
Frecuencia
v = λυ
Velocidad de
propagación
Longitud
de onda
El espectro electromagnético
El espectro electromagnético
es el conjunto de la radiación
electromagnética de todas las
longitudes de onda.
El espectro electromagnético no
tiene una frecuencia máxima o
mínima, sino que se extiende
indefinidamente, más allá de los
estrechos límites de sensibilidad del
ojo humano. En orden creciente de
frecuencias (y por tanto, de energía)
el espectro está compuesto por las
ondas de radio, ondas de TV,
microondas, el infrarrojo, la luz
visible, el ultravioleta, los rayos X
y los rayos gamma.
El espectro electromagnético
El efecto fotoeléctrico
El efecto fotoeléctrico fue descubierto
por Heinrich Hertz en 1887
Heinrich Hertz (1857-1894)
Físico alemán
El efecto fotoeléctrico consiste
en la obtención de una corriente
eléctrica mediante la iluminación
de un metal
El efecto fotoeléctrico
¿Será mayor la energía
de los electrones
liberados cuanto mayor
sea la intensidad de
iluminación?
¿Será entonces mayor el
número de electrones
liberados cuanto mayor
sea la intensidad de
iluminación?
Si eso es así el voltaje de
parada, V0, sería más
negativo para
intensidades luminosas
mayores
Si eso es así la intensidad
de la corriente medida por
el amperímetro
aumentará con la
intensidad luminosa
Interesante
Flash para
comprender
el efecto
fotoeléctrico
El efecto fotoeléctrico
¿Dependerá la velocidad de salida de los
electrones de la frecuencia (color) de
iluminación?
Si eso es así el voltaje de
parada, V0, sería más negativo
para frecuencias mayores
¿Habrá una frecuencia por
debajo de la cual no se
produzca efecto fotoeléctrico?
¿De qué depende dicha
frecuencia?
Si eso es así por debajo de
dicha frecuencia el voltaje de
parada es nulo.
El efecto fotoeléctrico
Según la teoría clásica (electromagnetismo clásico de Maxwell):
• La energía de los electrones emitidos debe ser tanto mayor cuanto mayor sea la
intensidad luminosa (mayor amplitud de la onda electromagnética, es decir, mayor
fuerza eléctrica aplicada al electrón)
• La intensidad de corriente eléctrica debe depender de la intensidad luminosa (en
esto coincide)
• La energía de la onda no depende de la frecuencia (color) de la onda, sino de su
amplitud, lo que no explica que los electrones reciban más energía cuando la
frecuencia de la luz crece
Albert Einstein
(1879-1955)
Físico
norteamericano
Según la interpretación de Einstein de 1905:
• La radiación está compuesta de unos paquetes indivisibles
de energía llamados fotones, con una energía que depende
de la frecuencia de dicha radiación según la expresión
E=hν
• Cada fotón, al alcanzar la superficie del metal interacciona con
un único electrón, el cual absorbe su energía
Frecuencia
umbral
1
hν = hν 0 + mv 2
2
Trabajo de
extracción
• La energía adquirida por el electrón se emplea en escaparse
del metal (trabajo de extracción) y el resto en aumentar su
energía cinética
Planck habla de que la radiación
electromagnética interacciona con la materia
en forma de cuantos energéticos.
Einstein habla de que la misma radiación
electromagnética
cuando
viaja
está
constituida por esos cuantos a los que él
denomina fotones.
Espectros atómicos
• La luz blanca se descompone haciéndola pasar por
un prisma de vidrio.
• El resultado se denomina espectro continuo de la
luz blanca, y contiene todas las frecuencias (colores)
visibles por el ojo.
• Un espectro es el resultado del análisis de las
distintas frecuencias que integran una radiación
electromagnética compleja.
Joseph von Fraunhofer
(1787-1826)
Óptico y físico bávaro
• Los espectros se obtienen con un espectroscopio o
espectrógrafo.
Gustav Kirchhoff
(1824-1887)
Físico alemán
Robert Bunsen (1811-1899)
Químico alemán
Espectros atómicos
• Los espectros pueden ser de emisión, cuando se analiza la radiación procedente de una
muestra excitada, o de absorción, cuando se analiza la radiación que ha atravesado la
muestra, es decir, la no absorbida.
• También pueden clasificarse en continuos: cuando proceden de muestras líquidas o
sólidas; y en discontinuos. Éstos a su vez pueden ser de bandas, propios de los gases
moleculares; o de líneas, correspondientes a los elementos en estado gaseoso.
Espectro de emisión
Espectro de absorción
Aquí puedes ver los
espectros de todos los
elementos
Aquí puedes ver los
espectros de todos los
elementos
Espectros atómicos
Espectro de
absorción del H
Espectro de
emisión del H
Espectro de
absorción del He
Espectro de
emisión del He
El espectro del hidrógeno
1885
SERIE DE BALMER
ν =
 1 1 
= RH  2 − 2 
λ
2 n 
1
RH = 10967757, 6 m
Johann Jakob Balmer
(1825-1898)
−1
Físico suizo
Constante de Rydberg
RESTO DE LAS SERIES DEL HIDRÓGENO
Johannes Robert
Rydberg (1854-1919)
Físico sueco
El espectro del hidrógeno
Carga núcleo: +Ze
Átomos
hidrogenoides
Carga electrónica: -e
FÓRMULA DE LOS ESPECTROSCOPISTAS
PARA ÁTOMOS HIDROGENOIDES
ν =
 1
1 
= RH Z 2  2 − 2 
λ
 n1 n2 
1
Serie de Lyman
n1=1
n2=2, 3, 4,…
Ultravioleta
Serie de Balmer
n1=2
n2=3, 4, 5,…
Visible
Serie de Pashen
n1=3
n2=4, 5, 6,…
Serie de Brackett
n1=4
n2=5, 6, 7,…
Serie de Pfund
n1=5
n2=6, 7, 8,…
Infrarrojo
El modelo atómico de Bohr
Los postulados del modelo atómico de Bohr fueron
publicados en 1913 y son:
• Los electrones giran alrededor del núcleo en
ciertas órbitas circulares estacionarias (no
emiten energía) con una energía definida. Estas
órbitas presentan estabilidad mecánica: Fe = Fc
• El átomo sólo emite energía cuando un electrón
cambia de una órbita a otra de menor energía;
esta energía se emite en forma de un cuanto
de radiación cuya energía, hν, es igual a la
diferencia de energías entre ambas órbitas:
(∆E=hν). Cuando el salto es el inverso esa
energía es absorbida por el electrón
• El electrón sólo puede girar en órbitas cuyo
momento angular esté cuantizado en
múltiplos enteros de h/2π: (m·v·r = n·h/2π =
n·ћ)
Niels Bohr (1885-1962)
Físico danés
El modelo atómico de Bohr
Del primer postulado Fe=Fc
mv 2
− Ze 2
=−
r
4πε 0 r 2
[1]
v=n
En cuanto a la energía:
nh
2π
Del tercer postulado, mvr =
1
− Z ·e 2
E = E p + Ec =
+ mv 2
4·π ·ε 0 ·r 2
h
2π mr
Operando, se obtiene:
Ze 2
m·v =
4πε 0 r
2
De [1]
h 2ε 0 n 2
n2
= a0
r= 2
eπ m Z
Z
1 Z ·e 2
1 Z ·e 2
Z
E=−
·
=−
2 4·π ·ε 0 ·r
2 4·π ·ε 0 a0 ·n 2
Ver
constantes
donde a0=0,52918 Ǻ es el radio de Bohr
El valor de la energía
depende de n, al que se le
denomina número cuántico
principal
y por tanto
Luego la energía correspondiente a la
órbita n es:
En =
− Z ·e 1
·
8·π ·ε 0 ·a0 n 2
2
2
El número cuántico
principal, n, determina el
radio de las órbitas así
como la energía de las
mismas
El modelo atómico de Bohr
De acuerdo con el 2º postulado
de donde
1
λ
=
E f − Ei
h·c
∆E = E f − Ei = hν = h
 1
1 
e 2 ·Z 2

=
−
8·π ·ε 0 ·a0 ·h·c  ni 2 n f 2 
c
λ
tomando
e 2 ·Z 2
8·π ·ε 0 ·a0 ·h·c
el valor de 109737,3 cm-1
sorprendentemente próximo al
de la constante de Rydberg
El modelo atómico de Bohr
El modelo atómico de Bohr
El modelo atómico de Bohr-Sommerfeld
El modelo atómico de Bohr, a pesar de su éxito y gran
aplicabilidad, se encontró muy pronto con dificultades:
• Explica los espectros del hidrógeno y de los átomos
hidrogenoides (un solo electrón) pero no los de los átomos
1
2
3
+
multielectrónicos1 H , 1H , 1H , 2 He
• El uso de espectroscopios de mayor poder resolutivo mostró la
llamada estructura fina del espectro del hidrógeno. En
realidad cada línea antes observada estaba constituida por un
conjunto de líneas muy próximas (dobletes, tripletes,
multipletes)
• En 1896 Pieter Zeeman descubre nuevos desdoblamientos
cuando el hidrógeno es sometido a un intenso campo
magnético. Efecto Zeeman
George Eugene
Uhlenbeck
(1900-1988)
Físico hidú
Arnold Sommerfeld
(1868-1951)
Físico alemán
• En 1925, Uhlenbeck y Goudsmit observan otro
desdoblamiento de las líneas de Zeeman. Efecto Zeeman
anómalo
Samuel Goudsmit
(1902-1978)
Físico germanonorteamericano
Pieter Zeeman
(1865-1943)
Físico holandés
El modelo atómico de Bohr-Sommerfeld
El modelo atómico de Sommerfeld introduce un número
mayor de cuatizaciones:
• Introduce una corrección de masa finita (consideración
de la masa reducida del sistema núcleo-electrón)
• Permite que las órbitas puedan ser elípticas, y cuantiza
las posibles formas de las mismas mediante el número
cuántico azimutal, l, con valores comprendidos entre 0 y
n-1
s =+1/2
• Para explicar el efecto Zeeman habla de orientaciones
de las órbitas en el espacio, que están cuantizadas
mediante el número cuántico ml, magnético, con
valores entre –l,…,0,…+ l
• Para explicar el efecto Zeeman anómalo introduce otro
número cuántico de spin, ms, asociado al giro del
electrón, y con dos posibles valores, +1/2, -1/2
s =-1/2
m=2
m=1
m=0
m=-1
m=2
m=1
m=0
m=-1
m=-2
m=-2
Campo
magnético
Dificultades del modelo Bohr-Sommerfeld
A pesar de la compleja formulación del átomo de
Sommerfeld y de sus aciertos en las ideas de
cuantización,
su
aplicación
en
átomos
multielectrónicos seguía siendo complicada y daba
pobres resultados.
Además el átomo de Bohr-Sommerfeld resultaba ser
una mezcla, a veces aparentemente arbitraria, de
Mecánica Clásica y de Mecánica Cuántica
Werner Heisenberg
(1901-1976)
Físico alemán
Erwin Schrödinger
(1887-1961)
Físico austríaco
Hacia 1925 existían ya numerosas razones para
pensar en abandonar la teoría de Bohr-Sommerfeld
La solución a todas estas dificultades se obtiene con
el desarrollo de un nuevo tipo de Mecánica, la
llamada Mecánica Cuántica. Así, en 1925, dos
jóvenes físicos, Werner Heisenberg y Erwin
Schrödinger,
de
manera
independiente,
resolvieron magistralmente el problema de la
constitución atómica creando una doctrina que fue
ampliada y estructurada posteriormente por Born,
Jordan y Dirac.
Pascual Jordan
(1902-1980)
Físico alemán
Paul Dirac
(1902-1984)
Físico británico
Max Born
(1882-1970)
Físico alemán
Los principios del modelo atómico actual
Heisenberg
Schrödinger
MECÁNICA DE MATRICES
MECÁNICA ONDULATORIA
Hipótesis de
Planck
Principio de incertidumbre
de Heisenberg
Principio de dualidad
onda-partícula de
Louis de Broglie
La dualidad onda-partícula
Louis Víctor de Broglie
(1892-1987)
Físico francés
En 1924 Louis Víctor de Broglie, a
raíz de los resultados de Planck y
Einstein habla de que la naturaleza
dual de la materia
• Según el duque de Broglie, la
materia presenta unas veces su
naturaleza ondulatoria y otras su
naturaleza corpuscular
h
λ=
mv
Longitud de
onda asociada
Constante de
Planck
Velocidad de
la partícula
• De manera que toda partícula con
masa lleva asociada una onda
cuya lontigud de onda está
determinada por la expresión de de
Broglie
Masa de la
partícula
La dualidad onda-partícula
• En 1927 Davisson y Germer obtienen figuras de difracción
de un haz de electrones, confirmando así la hipótesis de
Broglie
• La difracción de neutrones, protones, átomos de He, apoyan la
idea de la dualidad
• Inventos tan importantes como el microscopio electrónico tienen
su base de funcionamiento en la dualidad onda-partícula
Fotografía con
microscópio electrónico de
barrido de un linfocito T
Diagrama de difracción de
rayos X al pasar a través
de una lámina de aluminio
Joseph Davisson
(1881-1958)
Halbert Germer
(1896-1971)
Físicos estadounidenses
Diagrama de difracción de
electrones al pasar a través
de una lámina de aluminio
El principio de incertidumbre de Heisenberg
En 1927 Heisenberg postula que cuando se realizan medidas simultáneas de dos
variables que él denomina conjugadas, x e y, el aumento en la precisión en la
medida de una de ellas afecta negativamente (disminuyendo) a la de la otra
• La precisión o incertidumbre de la que habla Heisenberg no depende del
instrumento de medida. En realidad, aunque el instrumento utilizado fuera
infinitamente preciso, se seguiría cometiendo error en la medida de las variables
conjugadas, de tal forma que el producto de sus incertidumbres siempre será
mayor que la constante de Planck dividida por 4Π. Es la propia medida la que
altera el sistema a medir haciendo imposible precisar la magnitud conjugada
• Heisenberg establece como variables conjugas a la posición y la cantidad de
movimiento de una partícula, así como a la energía y el tiempo
∆x·∆p ≥
Incertidumbre
en la posición
h
4·π
Incertidumbre
en la cantidad
de movimiento
Principios de la Mecánica Cuántica
• El conocimiento del estado de un sistema en Mecáncia Cuántica implica siempre menos
información que en Mecánica Clásica
• La Mecáncia Cuántica de Schrödinger no es deducible. Se justifica a posteriori porque explica
correctamente el comportamiento de los sistemas atómicos (también los macroscópicos)
• Esta teoría cuántica se formula mediante postulados
PRIMER POSTULADO
El estado de un sistema está definido por una función de las
coordenadas y del tiempo, Ψ(x,y,z,t), que se denomina función de
onda o función de estado y que se describe como una amplitud de
probabilidad
La función valor absoluto de Ψ al cuadrado,│Ψ│2, es la densidad de
probabilidad de encontrar el sistema de partículas en unas
coordenadas del espacio
TERCER POSTULADO
La amplitud de probabilidad o función de onda de un sistema
mecanocuántico, Ψ= Ψ (x,y,z,t) debe satisfacer la ecuación diferencial
⌢
∂Ψ
H Ψ − iℏ
=0
∂t
ECUACIÓN DE SCHRÖDINGER DEPENDIENTE DEL TIEMPO
SEGUNDO
POSTULADO
A cada variable
dinámica u
observable del
sistema
mecanocuántico
le corresponde un
operador lineal
hermítico
La Mecánica Cuántica en los átomos hidrogenoides
La aplicación de la Mecánica Cuántica al átomo nos lleva a la siguiente ecuación de
Schrödinger
ℏ 2  ∂ 2ψ ∂ 2ψ ∂ 2ψ
−
+
+
2µ  ∂x 2 ∂y 2 ∂z 2
 Ze 2
 − 4πε r ψ = Eψ

0
Cuya resolución (realizada por Dirac) nos proporciona la función de onda Ψ cuyo producto
|Ψ|2 representa la probabilidad de encontrar al electrón en una zona del espacio
ψ n ,l ,m (r , θ , φ ) = Rn ,l (r )·χ l ,m (θ , φ )
l
l
Como se ve, esta función de onda depende de unos números cuánticos, n, l y ml. Dichas
funciones se denominan orbitales atómicos y conforme los números cuánticos toman
valores se obtienen las zonas donde podemos encontrar a los electrones que rodean
al núcleo (orbitales). Estas funciones nos expresan la forma, energía, tamaño y
orientación de los orbitales
Algunas funciones asociadas de Laguerre o parte radial de la
función de onda
Resolución de la ecuación de Schrödinger
n l
Rn,l
Función
Z
2 
 a0 
1 0 R1,0
2 0 R2,0
2 1 R2,1
3 0 R3,0
3 1 R3,1
1 Z
 
2 2  a0 
3/ 2
1 Z
 
2 6  a0 
1 Z
 
9 3  a0 
3/ 2
1 Z
 
9 6  a0 
3/ 2
e − Zr / a0

Zr  − Zr / 2 a0
2
−

e
a
0 

3/ 2
Zr − Zr / 2 a0
e
a0

4 Zr 4Z 2 r 2  − Zr / 3a0
+
e
6 −
2 
a0
9a0 

3/ 2

2Zr  2 Zr − Zr / 3a0
4
−
e


3a0  3a0

Algunas funciones asociadas de Laguerre o parte radial
de la función de onda
Resolución de la ecuación de Schrödinger
Algunas funciones de onda completas (orbitales) para el
átomo de hidrógeno
Resolución de la ecuación de Schrödinger
n l ml
1 0
0
Función
Ψn,l,ml
Ψ 100 = Ψ 1s
1 1
 
π  a0 
3/ 2
3/ 2
2 0
0
Ψ 200 = Ψ 2s
2 1
0
Ψ 210 = Ψ 2pz
1 1
 
4 2π  a0 
3/ 2
1 1
 
4 2π  a0 
Ψ 211 = Ψ 2px
1 1
 
4 2π  a0 
2 1 -1 Ψ 21-1 = Ψ 2py
1 1
 
4 2π  a0 
2 1
1
3/ 2
3/ 2
e − r / a0

r  − r / 2 a0
−
2

e
a
0 

r − r / 2 a0
e
cos θ
a0
r − r / 2 a0
e
senθ cos φ
a0
r − r / 2 a0
e
senθ senφ
a0
Algunas funciones de onda completas (orbitales)
para el átomo de hidrógeno
Resolución de la ecuación de Schrödinger
n l
ml
3 0
0
Ψ 300 = Ψ 3s
3 1
0
Ψ 310 = Ψ 3pz
3 1 -1
3 1
1
Función
Ψn,l,ml
2

 r   r   − r / 3a0
 27 − 18   + 2    e

 a0   a0  

3/ 2



2
1
r  − r / 3a0
6
−
cos θ
  
e
a0 
81 π  a0  
1 1
 
81 3π  a0 
Ψ 31-1 = Ψ 3py
Ψ 311 = Ψ 3px
3/ 2
2 1
 
81 π  a0 
3/ 2
2 1
 
81 π  a0 

r  − r / 3a0
senθ cos φ
6 − e
a
0 

3/ 2

r  − r / 3a0
−
senθ senφ
6

e
a
0 

Algunas funciones de onda completas (orbitales) para el
átomo de hidrógeno
Resolución de la ecuación de Schrödinger
n l
3 2
3 2
ml
0
1
3 2 -1
3 2
2
3 2 -2
Función
Ψn,l,ml
Ψ 320 = Ψ 3dz2
1 1
 
81 6π  a0 
3/ 2
2
 r  − r / 3a0
(3cos 2 θ − 1)
  e
 a0 
3/ 2
Ψ 321 = Ψ 3dxz
2 1
 
81 π  a0 
 r  − r / 3a0
senθ cos θ cos φ
  e
a
 0
2
3/ 2
Ψ 32-1 = Ψ 3dyz
2 1
 
81 π  a0 
 r  − r / 3a0
senθ cos θ senφ
  e
a
 0
2
3/ 2
Ψ 322 = Ψ 3dx2-y2
1 1
 
81 π  a0 
 r  − r / 3a0
sen 2θ cos 2φ
  e
 a0 
2
3/ 2
Ψ 32-2 = Ψ 3dxy
1 1
 
81 π  a0 
 r  − r / 3a0
sen 2θ sen2φ
  e
 a0 
2
Algunas funciones de distribución radial de las
funciones de onda del átomo de hidrógeno en
función de la distancia al núcleo
Resolución de la ecuación de Schrödinger
Los orbitales atómicos
Orbital 1s
(1,0,0)
Orbital 2s
(2,0,0)
Los orbitales atómicos
Orbitales 2p
Orbital 2py
(2,1,-1)
Orbital 2pz
(2,1,0)
Orbital 2px
(2,1,+1)
Los orbitales atómicos
Orbitales 3d
Orbital
3dx2-y2
(3,2,2)
Orbital 3dxy
(3,2,-2)
Orbital 3dyz
(3,2,-1)
Orbital 3dxz
(3,2,1)
Orbital 3dz2
(3,2,0)
Los orbitales atómicos
Mueve los
orbitales aquí
Orbitales 4f
(4,3,1)
(4,3,-1)
(4,3,3)
(4,3,0)
(4,3,3)
(4,3,-1)
(4,3,-2)
(4,3,-3)
(4,3,2)
Los números cuánticos
Número cuántico
Principal
Símbolo
n
Valores
1,2,3,4,5,…
Significado
Determina la energía del orbital
Secundario o azimutal
l
Para cada n: 0,1,2,…,n-1
Determina parte de la energía
del orbital y la forma del mismo
Magnético
ml
Para cada l: -l,…,0,…+l
Determina la orientación en el
espacio
De espín
ms
1/2, -1/2
Relativo al giro del electrón
sobre sí mismo
Orbital
Electrón
Orbitales
Capa
K
n
1
L
2
M
3
N
4
Orbital
(3,2,1)
3dxy
l
0
0
1
0
1
2
0
1
2
3
-1
-3
-2
-1
-1
-2
-2
-1
-1
-1
Electrón
(3,2,1,+1/2)
m
0
0
0
0
0
0
0
0
0
0
1
1
1
2
1
1
1
2
2
3
Tipo
s
s
p
s
p
d
s
p
d
f
Representación
1s
2s
2p
3s
3p
3d
4s
4p
4d
4f
Nº electrones capa n=2n2
Energía orbital=f(n+l)
Nº de electrones
Nº
1
1
3
1
3
5
1
3
5
7
Orbitales
2
2
6
2
6
10
2
6
10
14
Capa
2
8
18
32
Diagrama de Möeller
Constantes de Física atómica
h = 6, 6256·10−34 J ·s
ℏ = 1, 0545·10−34 J ·s
e = 1, 602·10−19 C
K = 8,9874·109 Nm 2 / C 2
me = 9,1091·10−31 kg
m p = 1, 67252·10−27 kg
R = 10967760m −1
1eV = 1, 6·10−19 J
a0 = 5, 2917·10
−11
m = 0,53A