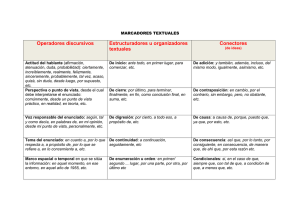
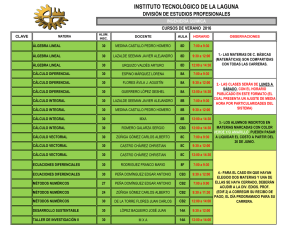
11. x²-9=8(x-2)

11.
x²-9=8(x-2)
x²-9=8x-16
x²-8x-9+16=0
x²-8x+7=0
=
x=
±
∗
=
±√
=
±√
=
±
= =7
x= = =1
La solución no es un solo número. Hay dos números que cumplen las condiciones del enunciado, son 1 y 7.
12.
n(n+1)-31=5(2n+1)
n²+n-31=10n+5
n²+n-10n-31-5=0
n²-9n-36=0
=
±
=
±
∗
=
±√
=
±√
=
= =12
Solución: el número que buscamos es el 12. He cogido sólo la solución positiva porque el enunciado nos dice que es nun número natural
13.
x* =27
x²=27*3
x²=81
x=√81
x=±9
Solución: Como el enunciado nos dice que el número es negativo, el número que buscamos es el 9
14.
x+x²=42
x²+x-42=0
(x+7)(x-6)=0
x+7=0  x=-7
x-6=0  x=6
Solución: como el enunciado nos pide un número positivo, el número que buscamos es el 6
15.
(
)²
x+11=
2(x+11)=(x-13)²
2x+22=x²-26x+169
x²-26x-2x+169-22=0
x²-28x-147=0
=
x=
±
=
= =21
±
x=
∗
=
±√
=
±√
=
±
= =7
Solución: hay dos soluciones, pero como no puede haber edades negativas y 7-13=-6, la edad actual de Marcela es 21 años.
16.
h=7-a
a=7-h
b=3m
Por el Teorema de Pitágoras sabemos que h²=a²+b²
(7-h)²+3²=(7-a)²
49-14h+h²+9=49-14a+a²
h²-14h-a²+14a=49-49-9
h²-14h-a²+14a=-9
a+h=7
Uso el método de sustitución , despejo hen la segunda ecuación y sustituyo en la primera
h=7-a
(7-a)²-14(7-a)-a²+14a =-9
49-14a+a²-98+14a-a²+14a=-9
a²-a²+14a+14a-14a=-9-49+98
14a=40
a=
a=2,86 m
h=7-2,86
h=4,14 m
Solución: el poste se rompió a una altura de 2,86 m
17.
Ancho=x, largo=y
x*y=600
x=y-10
Como tengo despejada la x en la segunda ecuuación, uso el método de sustitución, sustituyendo el valor de x en la
primera ecuación)
(y-10)y=600
y²-10y-600=0
y=
±√
=
±
∗(
)
=
±√
=
= =30 y=
= =-20
Como es una medida cogemos la solución positiva
.
=
±√ .
=
±
=
Ahora sustituimos el valor de y en una de las ecuaciones
x=y-10=30-10=20
Solución: las medidas de las revistas serán ancho=20 cm y largo=30 cm
18.
x+2√ =24
2√ =24-x
(2√ ) ²=(24-x)²
4x=24²-48x+x²
x²-48x-4x+576=0
x²-52x+576=0
=
=
±√
∗
= =36
=
±√
x=
=
±√
=
±
= =16
Solución: los números que cumplen las condiciones del enunciado son 16 y 36. Uno sería para el resultado positivo
de la raíz y otro para el resultado negativo. Es decir en x+2√ =24 , el resultado de √ puede ser negativo o positivo.
√16=±4, se cumpliría para el valor positivo y no para el negativo: 16+2*4=16+8=24. 16-2*4=16-8=8
√36=±4, se cumpliría para el valor negativo y no para el positivo: 36+2*6=36+12=48. 36-2*6=36-12=24
19.
Llamo x a la edad del padre, llamo y a la edad del hijo
√ =y
(√ )²=y²
x=y²
x+24=2(y+24)
x+24=2y+48
sustituyo el valor de x de la primera ecuación en la segunda
y²+24=2y+48
y²-2y+24-48=0
y²-2y-24=0
(x-6)(x+4)=0
x-6=0, x=6
x+4=, x=-4
Como no hay edades negativas la solución que nos vale es 6
Sustituyo el valor de y para hallar x
x=6², x=36
Solución: El padre tiene 36 años y el hijo 6.
20.
Numeros impares consecutivos. 2x+1, 2x+3. 2x+5
(2x+1)²+(2x+3)²+(2x+5)²=5.051
4x²+4x+1+4x²+12x+9+4x²+20x+25=5.051
12x²+36x+35=5.051
12x²+36x+35-5.051=0
12x²+36x-5.016=0 (simplifico dividiendo entre 12)
x²+3x-418=0
(x+22)(x-19)=0
x+22=0, x=-22
x-19=0, x=19
x=1=3
primer número impar que buscamos = 2*19+1=38+1=39
los dos siguientes son 41 y 43
Comprobación: 39²+41²+43²=1.521+1.681+1.849=5.051
Solución: los números impares son 39, 41 y 53
21.
19 cm
x
x+2
La diagonal forma dos triángulos rectángulos iguales donde los catetos miden x, x+2, y la hipotenusa 19.
Aplicando el Teorema de Pitágoras
19²=x²+(x+2)²
361=x²+x²4x+4
2x²+4x+4-361=0
2x²+4x-357=0
=
±√
∗ ∗
=
∗
±√
.
=
±√ .
=
±
,
=
,
12,4
Un cateto vale 12,4 y el otro 12,4+2=14,4
Solución: los lados del rectángulo son altura=12,4 y base= 14,4
22.
a+b=18
∗
=40
a=18-b
a*b=80
(18-b)b=80
18b-b²=80
b²-18b+80=0
b=
±√
b=
= 10
∗
=
±√
=
±√
=
±
b=
= =8
a=18-10=8
a=18-8=10
h²=a²+b²=8²+10²=64+100=164
h=√164 12,8
Solución: la medida de los lados del triángulo rectángulo son 8,10 y 12,8
23.
x*y=380
y=x+1
x(x+1)=380
x²+x=380
x²+x-380=0
=
x=
±√
∗
=
±√
∗
=
±√
=
±
= =19
x=
= =-20
y=19+1=20
y=-20+1=-19
Solución: los números que buscamos son -20 y -19, 19 y 20
24.
El volumen de la caja es largo x ancho x alto. Como la caja es cuadrada el largo y el ancho son iguales, luego será
lado² x alto. Como a cada lado le hemos cortado 5 cm el lado será x-5 y la altura será 5 cm que es la parte que
doblamos hacia arriba. Por tanto
(x-5)²*5=1280
(x²-10x+25)5=1280
5x²-50x+125=1280
5x²-50x+125-1280=0
5x²-50x-1155= 0 (simplfico dividiendo por 5)
x²-10s-231=0
=
±√
=
∗
=
±√
=
±√
=
±
= =21
=
= =-11
Como es una medida la solución es la positiva.
Solución la medida de los lados de la lámina de cartón es de 21 cm de lado
25.
altura= x, base=x+5
disminuimos 2, altura=x-2
(x-2)(x+5)=60
x²+5x-2x-10=60
x²+3x-10-60=0
x²+3x-70=0
=
=
±√
∗
=
±√
=
±√
=
±
= =8
=
= =-9
Como las medidas tienen que ser positivas alturas=8 cm
Base=x+5=8+5=13 cm
Solución: Base 13 cm y altura 8 cm