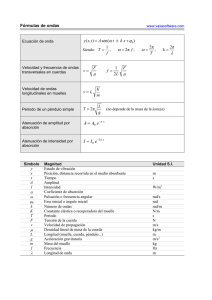
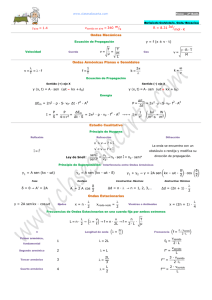
Lista 1 (estos ejercicios serán resueltos en clase)

Tema 2: Ondas
curso 01/02
Lista 1 (estos ejercicios serán resueltos en clase)
1. Una onda transversal se propaga en forma de ondas planas, en una región del espacio
ocupada por partículas de 1g de masa, siendo el desplazamiento de las mismas respecto
x t 
de su posición de equilibrio Ψ = 0,1 sen 2π −
 m , donde x se expresa en m y t en
 4 0,4 
s. Calcular:
1) La longitud de onda y la frecuencia angular del movimiento ondulatorio.
2) La velocidad de propagación de las ondas.
3) La energía cinética que, transcurridos 4 s, tendrá una partícula situada a 0,8 m del
foco.
4) En ese mismo instante, cuál es la mínima distancia al foco de otra partícula cuya
energía cinética sea la mitad de su energía total.
2. Una cuerda de 90 g y densidad lineal de masa 0,12 kg m −1 , está sujeta por sus
extremos, oscilando con una frecuencia de 50 Hz. Si la mínima distancia entre un nodo
y un vientre es de 12,5 cm:
1) Determinar en qué armónico oscila la cuerda.
2) Calcular la tensión a la que está sometida la cuerda.
3) Obtener la expresión del desplazamiento correspondiente a un punto de la cuerda
que está a 25 cm de uno de los extremos.
3. Un foco emite ondas sonoras planas, de intensidad 3 ⋅10 −4 W m −2 , de forma que los
dos primeros puntos en los que la expresión de la perturbación es Ψ = A sen ωt, distan
4 cm y 44 cm del foco:
1) Obtener la frecuencia de las ondas y la expresión de la función de onda en el foco.
2) Las ondas se reflejan en una pared colocada perpendicularmente a la dirección de
propagación, a 50 cm del foco, de forma que la reflexión introduce un cambio de fase de π rad. Sabiendo que la amplitud de la onda reflejada es A 3 , calcular en
cuántas posiciones puede colocarse un detector, situado entre el foco y la pared, para
medir una intensidad de 4 ⋅10 −4 W m −2 .
4. Dos focos F1 y F2 están separados una distancia de 75 m, y emiten simultáneamente
ondas planas de 250 Hz de frecuencia, que se propagan con una velocidad de 600 m s −1 .
El foco F1, que emite con amplitud A0, está adelantado π/2 respecto a F2. Si en un punto
P, situado entre ambos focos y a 25 m de F1, la amplitud de la perturbación resultante es
3 A0, obtener:
1) La expresión de la perturbación en P, correspondiente a cada una de las ondas.
2) La expresión de la perturbación resultante tras la interferencia en el punto P.
3) La máxima variación de nivel de intensidad que puede medirse a lo largo de la línea
que une ambos focos.
5. Una fuente emite ondas planas de 75 Hz de frecuencia, que se propagan con una velocidad de 300 m s −1 , siendo la ley de oscilación de la misma Ψ = A0 sen ωt. Si a 2 m
de ella se coloca una lámina, perpendicular a la dirección de propagación de las ondas,
tal que transmite el 64% de la intensidad y refleja el resto sin producir cambio de fase,
obtener:
1
Tema 2: Ondas
curso 01/02
1) La ley que expresa la oscilación de un punto equidistante del foco y de la lámina.
2) La diferencia entre el nivel de intensidad en el punto indicado, cuando no hay lámina y cuando sí la hay.
6. Dos focos puntuales emiten ondas esféricas de 75 Hz de frecuencia, que se propagan
con una velocidad de 300 m s −1 . La distancia entre los dos focos es 15 m y ambos emiten con la misma potencia, P = 16π W. Si en un punto O, situado entre ambos focos y
en la línea que los une, las ondas llegan en fase, y la diferencia de nivel de intensidad
cuando emiten los dos focos por separado es 6 dB, calcular:
1) La distancia del punto O a cada uno de los focos.
2) La diferencia de fase con que emiten los focos.
3) La intensidad en el punto O cuando emiten los dos focos simultáneamente.
7. Una cuerda, de 2 m de longitud y 20 g de masa, se tensa horizontalmente, empleando
para ello una masa m0 colgada mediante una polea, tal como se indica en la figura. Si
ambos extremos de la cuerda permanecen fijos:
1) Determinar cuánto vale m0, sabiendo que la
2m
velocidad de propagación de las ondas generadas en la cuerda es de 40 m s −1 .
2) Se tiene un oscilador mecánico que puede aplicarse para generar ondas en la cuerda, pero que
sólo funciona a tres frecuencias fijas: 15, 30 y
45 Hz. Determinar a qué frecuencia sería necem0
sario hacerlo funcionar para generar ondas estacionarias en la cuerda.
8. Un observador está situado en el punto medio de la línea que une dos focos sonoros
F1 y F2, separados entre sí una distancia d = 200 m. Ambos focos, que pueden desplazarse a lo largo de la línea recta que los une, empiezan a emitir, en el mismo instante,
ondas planas de la misma intensidad y frecuencias f1 = 200 Hz y f2 = 210 Hz, que se
propagan con una velocidad de 330 m s −1 . Si el primer foco se mueve hacia el observador, con una velocidad v1 = 30 m s −1 , determinar la velocidad que debe llevar el segundo foco para que el observador reciba las dos señales con la misma frecuencia, y el valor de la misma.
2
Tema 2: Ondas
curso 01/02
Lista 2 (ejercicios propuestos)
1. Un foco emite ondas planas de intensidad I; a una distancia d del mismo se sitúa una
lámina perpendicular a la dirección de propagación, que transmite parte de la intensidad
de la onda. Calcular el porcentaje de la intensidad incidente que se refleja, sabiendo que
en aquellos puntos situados entre la lámina y el foco, en los que se produce interferencia
constructiva, el valor de la intensidad es 2,25I.
2. Dos focos puntuales comienzan a emitir simultáneamente en el aire ondas sonoras de
frecuencias f1 = 10 kHz y f 2 = 11 kHz . Si el segundo foco se aleja del primero con
velocidad constante, calcular el valor que debería tener dicha velocidad para que un
observador situado en la línea que une los dos focos, observase alternativamente máximos y mínimos de intensidad.
3. Dos focos F1 y F2, separados entre sí 3 m, emiten ondas planas de frecuencia 75 Hz,
que se propagan con velocidad 300 m s −1 , emitiendo F2 adelantado π 2 respecto a F1.
Sabiendo que la amplitud de la señal producida por F1 es A y la de F2 es 2A:
1) Obtener la expresión de la perturbación
F2
F1
O′
O
correspondiente al punto O de la figura.
1m
1m
2) Calcular la diferencia de nivel de intensidad
3
m
entre las señales recibidas en O y en O′.
4. Una cuerda de 2,4 m de longitud está sujeta por ambos extremos y sometida a una
tensión de 12 N. Cuando en la cuerda se propagan ondas estacionarias de 20 Hz de frecuencia, se observa que el punto más próximo a uno de los extremos, para el que la amplitud es la mitad que la correspondiente a un vientre, es el situado a 10 cm de dicho
extremo:
1) Determinar en qué armónico oscila la cuerda.
2) Calcular la masa de la cuerda.
5. El extremo de una cuerda tensa se desplaza de su posición de equilibrio siguiendo la
ley Ψ = 5 sen 100 π t cm . Si en un cierto instante la distancia entre dos puntos consecutivos, que se encuentran en su posición de equilibrio, es 20 cm, calcular:
1) La velocidad con que se propagan las ondas en la cuerda.
2) La velocidad de un punto de la cuerda situado a 1 m del extremo.
3) El tiempo que tarda dicho punto en pasar dos veces consecutivas por su posición de
equilibrio.
6. Dos focos F1 y F2 emiten con la misma potencia P, ondas esféricas cuya longitud de
onda es λ. Si un observador situado a distancias r de F1 y 3r de F2 percibe un nivel de
intensidad 10 dB superior cuando emiten los dos focos que cuando sólo emite F2:
1) Calcular la diferencia de fase con que las dos ondas llegan al punto indicado.
25
2) Si r = λ , ¿con qué diferencia de fase emiten los focos?
8
7. Cuatro focos iguales F1, F2, F3 y F4, que están situados en los vértices de un cuadrado
de lado 2 2 m, emiten ondas planas transversales de frecuencia angular ω, longitud de
onda 1 m y amplitud Ψ0. El foco F1 está adelantado π 2 respecto a F2, éste lo está π 2
3
Tema 2: Ondas
curso 01/02
respecto a F3 y éste también π 2 respecto a F4. Considerando que F1 tiene fase inicial
nula y que las ondas generadas por los cuatro focos van dirigidas hacia el punto P situado en el centro del cuadrado, calcular:
1) La expresión de la perturbación en el punto P cuando sólo emiten F1 y F2 y cuando
sólo lo hacen F3 y F4.
2) La expresión de la perturbación en P cuando emiten los cuatro focos.
3) El nivel de intensidad en P cuando sólo emiten F1 y F2, si cuando sólo emite F1 es
de 42 dB.
8. Dos cuerdas de la misma longitud, una de acero y otra de cobre, están sometidas a la
misma tensión. Ambas vibran en el modo fundamental, de forma que la relación entre
las frecuencias emitidas es 2/3, siendo la de cobre la que emite el sonido más agudo. Si
las densidades del acero y del cobre son 7,5 ⋅103 kg m −3 y 8,9 ⋅103 kg m −3 respectivamente, calcular:
1) La relación entre los diámetros de las cuerdas.
2) La relación que debería existir entre las longitudes de ambas cuerdas para que, sometidas a la misma tensión y vibrando las dos en el modo fundamental, la de acero
emitiese una frecuencia igual a la mitad de la frecuencia emitida por la de cobre.
4