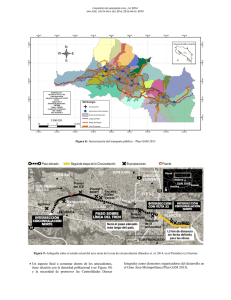
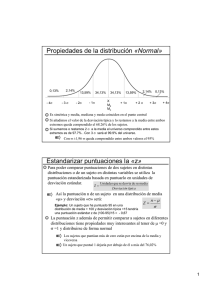
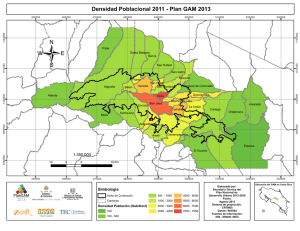
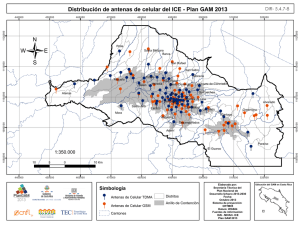
ij - Portal de revistas académicas de la Universidad de Costa Rica

Ciencias Económicas 31-No.2: 2013 / 135-156 / ISSN: 0252-9521
ANÁLISIS DE LA DINÁMICA REGIONAL DEL EMPLEO UTILIZANDO
EL MODELO SHIFT SHARE ESPACIALMENTE MODIFICADO
EN LA GRÁN ÁREA METROPOLITANA (GAM) DE COSTA RICA
PARA EL PERIODO 2000-2011
Rafael Arias Ramírez1
Leonardo Sánchez Hernández2
Recibido: 04/09/2013
Aprobado: 08/10/2013
RESUMEN
Este artículo es resultado de un estudio más amplio que se está realizando sobre patrones
de concentración y evolución de la localización industrial y del mercado laboral en la
Gran Área Metropolitana (GAM) de Costa Rica y forma parte de la investigación que
en economía regional ha venido realizando el Instituto de Investigaciones en Ciencias
Económicas (IICE) de la Universidad de Costa Rica desde el año 2005. El presente artículo
plantea una aproximación a la dinámica regional del empleo en la GAM durante el periodo
2000-2011 mediante la aplicación del análisis Shift-Share en sus formulaciones clásica y
espacialmente modificada. Esto permite descomponer el crecimiento del empleo en cuatro
efectos: el efecto nacional, el efecto sectorial, el efecto regional o competitivo y el efecto
“locacional”.
PA LA BR AS CLAVES: GR A N Á REA METROPOLITA NA, MERCADO L A BOR AL, ECONOMÍ A
REGIONAL, SHIFT-SHARE, AUTOCORRELACIÓN ESPACIAL, ESPECIALIZACIÓN, VENTAJAS
COMPETITIVAS.
ABSTRACT
This article is a result from a broader study on the patterns of concentration and evolution
of the process of industrial localization and the labor market in the Great Metropolitan
Area of Costa Rica (GAM). This study is part of the research program on regional
economics that the Institute of Research in Economic Sciences of the Universidad de
Costa Rica (IICE) has been conducting since the year 2005. The article is aimed to show
an approximation to the regional dynamics of employment in the GAM in the period 20002011. In order to do that we applied the Shift-Share analysis in its classic and spatially
modified formulations. This allows us to decompose employment growth in four effects:
the national effect, the sectorial effect, the regional effect and the “locational” effect.
KEY WORDS: GREAT METROPOLITAN AREA, LABOR MARKET, REGIONAL ECONOMICS, SHIFTSHARE, SPATIAL CORRELATION, SPECIALIZATION, COMPETITIVE ADVANTAGES.
1
Universidad Nacional, profesor Escuela de Economía, UNA, Código Postal 86-3000, Costa Rica; rarias@una.ac.cr
2
Universidad de Costa Rica, investigador del Instituto de Investigaciones en Ciencias Económicas (IICE) y del
Programa de Desarrollo Urbano Sostenible (PRODUS), Código Postal 11501- 2060,joseleonardo.sanchez@ucr.ac.cr
136
Rafael Arias Ramírez y Leonardo Sánchez Hernández
I.INTRODUCCIÓN
En este artículo se plantea una aproximación a la dinámica regional del empleo en la Gran
Área Metropolitana (GAM) durante el periodo 2000 - 2011 mediante la aplicación del análisis shiftshare, en sus formulaciones clásica y espacialmente modificada. Esto permite descomponer el crecimiento del empleo en cuatro tipos de efectos: nacional, sectorial, regional o competitivo y el “locacional”. Para ello, se utilizaron los censos de población y vivienda para los años 2000 y 2011.
En la actualidad, una de las técnicas estadísticas de análisis regional más utilizadas para
examinar las diferencias observadas en el crecimiento económico de distintas áreas geográficas
(países, regiones, municipios, etc.) es el método Shift-Share (Dunn, 1960). Como es bien conocido,
el análisis Shift-Share tradicional descompone el crecimiento de variables económicas regionales
(como la renta, el empleo, el valor añadido, etc.) en tres componentes aditivos: uno relativo al área
supra-regional de referencia (denominado efecto nacional), otro relativo a la estructura productiva
de la región (efecto estructural o sectorial), y un componente diferencial región-nación (efecto competitivo o regional).
Desde su primera formulación, la técnica Shift-Share ha sido sometida a numerosas revisiones o extensiones (ver, entre otros, Esteban-Marquillas (1972), Haynes y Machunda (1987), Haynes y
Dinc (1997) y Nazara y Hewings (2004)), con el objetivo de intentar solventar algunos de los inconvenientes que presenta el modelo básico (ausencia de contenido teórico, problemas de agregación,
interdependencia de los efectos sectorial/regional, inestabilidad estructural y limitaciones de tipo
inferencial, entre las más importantes).
A pesar de sus debilidades, el análisis Shift-Share ha sido ampliamente utilizado en el contexto del análisis económico regional tanto con fines predictivos (Gerking y Barrington (1981) y
Andrikoplous et al. (1990)), para la evaluación de políticas (Bartels et al (1982) y Mcad y Ramsay
(1982)) o para planificación estratégica (Ledebur y Moomaw (1983), Senf (1988)). Ello se explica
porque no necesita grandes conocimientos técnicos para su aplicación (Stevens y Moore (1980)). El
análisis requiere una información estadística que suele estar disponible de manera fácil y considera
el ámbito nacional como marco de referencia a la hora de analizar el desarrollo regional (Nijkamp
et al. (1986)).
Dado el creciente interés en el ámbito de la economía en general y de la economía regional en
particular, por determinar la influencia del espacio en los modelos de crecimiento económico y en
los procesos de convergencia entre las distintas unidades económicas, es que nos plantemos como
objetivo de esta sección llevar a cabo una ampliación del análisis Shift-Share estándar para tener en
cuenta la localización geográfica como un marco de referencia relevante.
Entre otras cosas, dicha ampliación permitirá detectar patrones de comportamiento que pueden ayudar a determinar los factores que subyacen en las disparidades existentes entre las diferentes
regiones de planificación definidas por el MIDEPLAN y plantear y responder cuestiones como: ¿Está
la estructura económica regional diseñada atendiendo a la media nacional? o ¿Está la estructura
económica regional atendiendo a las características de la propia región? Además, se pretende ofrecer
una formulación espacial general del modelo shift-share, la cual permita integrar dentro de la identidad contable de crecimiento regional del empleo en la Gran Área Metropolitana, tanto los efectos
clásicos (nacional, sectorial y regional) como el efecto locacional, derivado de la existencia de interrelaciones espaciales entre las distintas unidades económicas analizadas.
II. Elementos teóricos del análisis shift-share: modelo clásico,
modificaciones y extensiones
La técnica Shift-Share es un instrumento de análisis regional de gran utilidad. Su objetivo no
es otro que el de descomponer el crecimiento regional, observado en un periodo de tiempo, en una
Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521
CLÁSICO,
Y EXTENSIONES
concreta.
la tasa
de cr
II. con
TEÓRICOS
DEL
ANÁLISIS
SHIFT-SHARE:
MODELO
concreta.
la
tasa
de
crecimiento
en
elelinterpretación
empleo
del MODIFICACIONES
sector
en
la económica
región
j , Así
i observado
do de tiempo,
en
una
serie
de
factores
una
económica
objetivo
no
es
otro
que
eluna
de
descomponer
crecimiento
regional,
en
un
periodo
deAsí
tiempo,
en
serie
deELEMENTOS
factores
con
una
interpretación
objetivo
no
es
otro
que
el de
descomponer
el
crecimiento
regional, observad
producido
los periodos
MODIFICACIONES
Yj ,EXTENSIONES
producido
entre
periodos
y empleo
,CLÁSICO,
es:
eta. Así periodo
la tasa de
de
crecimiento
encrecimiento
delelsector
en
lasector
región
telserie
t  mde
tiempo,
endeuna
factores
coni una
una
interpretación
concreta.
Así
lalostasa
en
empleo
del serie
en
la económica
región
j , entre
periodo
tiempo,
en
deiesfactores
con una
ecod
La técnica
Shift-Share
un instrumento
de interpretación
análisis regional
concreta.
Así tlalos
en la
el tasa
empleo
del
sector i enenellaempleo
región del
j , sector i en la re
cido entre
los periodos
y tasa
es:crecimiento
t
m ,de
concreta.
de
crecimiento
producido
entre
periodos
es:
t y t  m , Así
objetivo no es otro que el de descomponerEel(tcrecimiento
m)  Eij (tde
) regiona
regional
Eij (tu
La, entre
técnica
Shift-Share
es
un
instrumento
de análisis
gran
Eij (t entre
m)  los
Eij (tperiodos
) Eij (tproducido
) m
ij
producido
es:
t ym,tt 
los
periodos
y
,
es:
t
t

m
periodo
de
tiempo,
en
una
serie
de
factores
con
una
r

interpr
ij
r ij 

(1)
objetivo
no
es
otro
que
el
de
descomponer
el
crecimiento
regional,
observa
Eij (t137
) del sector
Eij
Eij (t  m)  Eij Análisis
(t )Eij (tde
(tt) E
mij,(tt)) regional
) , t ) utilizando
tij (templeo
m
EEm
EijE(del
ijla
el modeloAsí
shiftla
share...
concreta.
tasa de crecimiento en el empleo
ij )(dinámica
periodo
de (1)
tiempo, en una serie de factores con una interpretación e
r ij  E(t  m)  E (t )  E ((1)
t
m
,
t
)

Eij (t producido
m)  Eij (t ) entre
, t)
Eij (t  m
Eij (t )
ij
ijE (t )
periodos
es:
t yent elm ,empleo
EijE(ijt()t ) ij 
ijr ij
r ij 
concreta.
Así
del sector i en la

 deloscrecimiento
(1) la tasa
(1)
E
(
t
)
E
(
t
)
Expresado
E
(
t
)
E
(
t
)
serie
de factores
interpretación
económica
concreta.
Así
la
tasa
de
crecimiento
en
el
empleode otra forma
ij
ij
Expresado
decon
otrauna
forma,
tenemos:
ij
ij
producido entre los periodos t y t  m , es:
Eij (t  m)tyEt ij+(tm,
) es:
Eij (t  m, t )
sector
i en de
la región
j, producido
entre los periodos
Expresado dedelotra
forma,
tenemos:
Expresado
otra forma,
tenemos:

(
Eij (1)
(t  m, t )  Eij (t )rij
(2)tenemos:r ij 
Eij (tExpresado
 m, t )  Eij (de
t )rijotra forma,
E (t) Eij (t tenemos:
Expresado
Eij (t  m) de
 Eotra
 m, t ) Eij (t )
ij (t ) ijforma,
(1)

(2)(t )r
(1)
 m, t )  Eij E
(tij)(rijt  m, t )  E
(2)r ij 
ij
ij
Eij (tde
) crecimiento
Eij (tespecífico
)
El resultado
es
consecuencia
del ratio
obtenido porElelresultado es consecu
(2)
(2)otra forma, tenemos:
Eij (t  m, t )  Eij (t )rij
Eij (dato
t  m, se
t )  ha
Eij (Expresado
tproducido
)rij
de
i en la región r . Es
sector
en
la región
Este
en específico
un entorno
mássector
general
iresultado
r .ratio
El resultado
esElconsecuencia
del
detenemos:
crecimiento
específico
obtenido
por elobtenido
Expresado
otra
forma,
esdeconsecuencia
del ratio
de
crecimiento
por el
*
*
(resumido,
al menos, por
ri* y
(resumido,
por
y r*producido
como
tasas
crecimiento
del
sector
y de
delcrecimiento
agregado
i obtenido
región
dato
ha
ende
un
entorno
general
i en la sector
r . alEste
El iresultado
es
consecuencia
ratio
de
crecimiento
específico
por el específico
Expresado
de
otra forma,
tenemos:
en
lamenos,
región
. riEste
dato
se
ha
producido
enmás
un
entorno
más
general
rse
El del
resultado
es
consecuencia
del
ratio
obtenid
(2) de la eco
(2)
Eha
tdel
producido
msector
, t )puede
 Eij i(ten
)yser
rijdel
*
ij (región
total
en en
el conjunto
sector
enconjunto
. reconomía
Este
sela
un
entorno
general
iel
rtasas
mido, al menos,
y región
de* dato
crecimiento
agregado
r** como
ri*lamenos,
total enpor
depor
la
que
interesante
conocer
para
sector
en
dato
se ha más
producido
un entorno
más
inacional)
r . Este
(resumido,
al
i y r* como tasas de crecimiento del sector i y del agregado
*
*
*
*
*
(2)
E
del
m
, tratio
)menos,
ser
EEl
(interesante
tresultado
)crecimiento
rijpor
valorar
mejor
ese
crecimient
(resumido,
al
menos,
como
tasas
de
crecimiento
del
sector
y
del
agregado
r*que
i
ri y(resumido,
resultado
es
de
específico
obtenido
por
el
sector
i
en
en el conjunto
demejor
laElconjunto
economía
nacional)
conocer
para
r

r

r
al
como
tasas
de
crecimiento
del
sector
y
del a
r
i
ri* yser
valorar
ese crecimiento.
En
general,
se
verificará
que:
,
por
lo
que
ij (t puede
ijque
total
en
el
depor
laconsecuencia
economía
nacional)
puede
interesante
conocer
para
* del ratio de crecimiento específ
ij
i
es* consecuencia
* y r *
* general
*
*
*conocer
la
región
r.
Este
dato
se
ha
producido
en
un
entorno
más
(resumido,
al
menos,
por
r
en
el
conjunto
de
la
economía
nacional)
que
puede
ser
interesante
para
retomando
la
anterior
expresió
r

r

r
r mejor total
ese
crecimiento.
En
general,
se
verificará
que:
,
por
lo
que
sector
la economía
.nacional)
Este
producido
en unconoc
en
totalpodemos
en general,
el conjunto
de
que
puede
seri interesante
*
retomando
la anterior
expresión
escribir:
del
ri ratio
 rdato
valorar
mejor
ese crecimiento.
En
sei en
verificará
porse
loha
que
* que:rrij
ij la
i región
* , de
El iresultado
es
consecuencia
crecimiento
específico
obten
* la economía
*
*
* * * de
comomejor
tasas ese
de crecimiento
del sector
y(resumido,
delese
agregado
total en
el
conjunto
nacional)
r

r

r
valorar
crecimiento.
En
general,
se
verificará
que:
,
por
lo
que
al
menos,
por
y
como
tasas
de
crecimiento
del
sect
r
r
r

r

r
valorar
mejor
crecimiento.
En
general,
se
verificará
que:
,
por
ando la anterior
expresión
podemos
escribir:
*
ij
i
i
*
i
retomando
la anterior
expresiónsector
podemos
la región r . Este dato
se* ha producido* en unij * entorno
má
i en escribir:
*
conocer
para
valorar mejor
ese crecimiento.
En general,se
que:
Eij verificará
 r* que
Eij (t )puede
 ri  rser
(t )  r
Eijque
 r**puede
Eij (la
t ) ser
ri*interesante
 r** E
rij (resumido,
podemos
ri* E
* de* la economía nacional)
* Eijintere
retomando
anterior
expresión
escribir:
en (3)
el expresión
conjunto
ij (t )  retomando
ij (t )total
la al
anterior
podemos
escribir:
menos,
por
y
como
tasas
de
crecimiento
del
sector
y
del
r
i
r
*
*
* escribir:
i
lo
podemos
r *ri r* , por
* que retomando
* la anterior expresión
r** Eij (t )  riE* ij ijr**r*E
(3)
Eij ij(t()t )rijri*rir**EEij ij(t()t )  rij total
 r(3)
E
(
t
)
r
valorar
mejor
ese
crecimiento.
En
general,
se
verificará
que:
ij el conjunto de la economía nacional) que puede
ij 
ser interesante
con
El crecimiento
regiona
El crecimiento regional eni* en
el
empleo
en tres
* (3)
*del sector i * se desglosa
(3)
(3)
Eij  r** Eij (t )  ri*  r** Eij (t )  
rijEij ri rE**ijE(ijt ()retomando
*
*
t
)

r

r
E
(
t
)

r

r
E
(
t
)
i ese* crecimiento.
ij anterior
ij
i
ij general,
expresión
escribir: que: rij  ri  r* , p
valorar
secomponentes:
verificará
componentes:
El crecimiento
en el
empleo
sector
i del
sela
desglosa
en
trespodemos
El regional
crecimiento
regional
endel
el mejor
empleo
sector i En
se
desglosa
en
tres*
*
j
i j .desglosa
 r* Eij (ti) se
Es el cre
El
crecimiento
regional
en
el
empleo
del
sector
i
se
desglosa
en
tres
componentes:
onentes: componentes:
(
t
)


 r* E
.
Es
el
crecimiento
que
habría
experimentado
la
variable
regional
El
crecimiento
regional
en
el
empleo
del
sector
i
se
desglosa
en
tres
retomando
la
anterior
expresión
podemos
escribir:
ij
i
El crecimiento
regional
del sector
*
*
*en el empleo
*
(3)
*
j

E

r
E
(
t
)

r

r
E
(
t
)

r

r
E
(
t
)
j
* ij
*
ij
i
ij regional
i
ij caso, de haber evolucionado
i . Es
 r* Eij (t ) componentes:
crecimiento
que componentes:
habría
experimentado
la variable
caso,
de
haber
evolucionado
al mismo
ritmo
que
loexperimentado
ha
hecho
el
agregado
nacional
en
r** Eel
que
habría
la ijvariable
regional
ij (t )  
i . Es el crecimiento
*
*
*
*
*
j
*
j
(3)
su
conjunto.

E

r
E
(
t
)

r

r
E
(
t
)

r

r
E
(
t
)
r* Ehaber

- de
Es
el
crecimiento
que
habría
experimentado
la
variable
regional
caso,
haber
.
Es
el
crecimiento
que
habría
experimentado
la
variable
regional
suevolucionado
conjunto.
r
E
(
t
)



.
Es
el
crecimiento
que
habría
experimentado
la variable
*
*
ij
ij
i
ij
ij
i
ij
de habercaso,
mismo
ritmo
que
lo
ha
hecho
el
agregado
nacional
en
ij (t )  al
i
crecimiento
en nacional
el empleo
sector
i se
* ij ritmo El
i
evolucionado al mismo
que
lo ha hecho regional
el agregado
en*dedel
*
*
*
j
r

r
E
(
t
)
 i j . Parte

njunto. caso,
r

r
E
(
t
)



.
Parte
de
que
la
discrepancia
entre
el
crecimiento
observado
i
*
ij
de
haber
evolucionado
al
mismo
ritmo
que
lo
ha
hecho
el
agregado
nacional
en
componentes:
evolucionado
al mismo
ritmo
ha hecho
el agregadoalnacional
en su conjunto.
su conjunto.
i
*
ij
i
caso, que
deEllo
haber
evolucionado
mismo
ritmo
que
lo
ha
hecho
el
agregado
nac
crecimiento
regional
en el empleo del sector i se desglosa
j*
*
j
*
j
conjunto.
j que laentre
(
t
)


 ri*  r** Esu
.
Parte
de
que
la
discrepancia
el
crecimiento
observado
su
conjunto.
r
E
(
t
)



.
Es
el
crecimiento
que
habría
experimentado
l
r

r
E
(
t
)


(

E
(
t

m
,
t
))

.
Parte
de
discrepancia
entre
el
crecimiento
observado
y
el
estándar
ij
i
Parte
de
que
la
discrepancia
entre
el
crecimiento
observado
y
el
-
(Eij (t i*m, t ))
ij
i
yij el estándar
( componentes:
el sector
 i ) se debe a *que
i ha crecido de forma
*
i
ij
*
j
*
*
j
r

r
E
(
t
)



.
Parte
de
que
la
discrepancia
entre
el
crecimiento
observado
j
*
j
r

r
E
(
t
)



.
Parte
de
que
la
discrepancia
entre
el
crecimiento
ob
j quei elcaso,
*
i debe
de
evolucionado
al
mismo
que
ha hecho
el
ag
i ha
diferente
aello
como
lolahavariabl
hech
t  m,t )) diferente
y(E
elij (estándar
se
debe
ael
crecido
de
forma
ihaber
se
a que
elconjunto
sector
i(tha
dees
forma
diferente
a como
lo
ha
hecho
con)ijnacional;
acrecido
que
 r E*ijsector
el
crecimiento
que
habría
experimentado
como
ha
hecho
decir,
sido
más
o ritmo
menos
t estándar
i ma, t ))
yij( eli lo)estándar
(
el
sector
ha
crecido
de
forma
i ha
i . Es
i ) se * debe
*
*
j
*
*(
j i ha crecido
su
conjunto.
dinámico
que
la
media
r

rn
(

E
(
t

m
,
t
))
*
*
y
el
estándar
)
se
debe
a
que
el
sector
de
forma


Esido
más
m, tes
))
dinámico
la media
. caso,
ri hecho
 r*(ha
ynacional;
elevolucionado
estándar
( al
) mismo
semenos
debe
ar* que
el ha
sector
crecido
d*
i
nte a como
ha que
elloconjunto
nacional;
decir,
ha * sido
más
omedia
ijlo junto
iij (tconjunto
. o menos
nacional;
es
o menos
dinámico
que
rritmo
de
haber
lo
hechoi elhaagregado
diferente
ahecho
como
hadecir,
el
es decir,
i la
i más
*
j ha sido
* * *
r
*
ri  r* Ees
 i . ha
 lo
Parte
denacional;
queolamenos
discrepancia
entre
el
crec
* su
r a
j *hecho
ij (t )
diferente
lo ha
conjunto
nacional;
decir,
ico que la
media
rla. media
rrdecir,
 i j más
 encontrado
. La
dio
a como
ha
es
ha
dinámico
. el conjunto.
r La
 rdiferencia
i 
rcomo
restante
debe
a que
elconjunto
sector
en
la región
diferencia
restante
sese
debe
ahecho
que
elelsector
isido
en ilamás
región
r ha
-  ri rque
i  ri E
ij (t )sido
*diferente
i *Eij (t )  i . i La
*
*
j
*
*
j
*
*
r
*
j r que
. se debe
r

r
E
(
t
)



.
Parte
de
que
la
discrepancia
entre
el
crecimiento
* la mediaj ri  r*dinámico
(

E
(
t

m
,
t
))
y
el
estándar
(
)
se
debe
a
que
el
sector
ha

i
que
la
media
.
r

r
i
*
ij
i
ha
encontrado
unas
condicio
(
t
)


ij
i
 ri  ri Edinámico
.
La
diferencia
restante
a
que
el
sector
en
la
región
i
r
i
ha
económicas
específicas
que
dificultan)
ri i  rcondiciones
(t )  condiciones
específicas
dificultan)
losu
que
 unas
. La diferencia
restanteque
sefacilitan
debe
a*(o
que
elfacilitan
sectorsui(oexpansión,
en
la región
r le perij encontrado
i Eijunas
i económicas
r
*
j
r
*
j como lo haj hecho el conjunto
expansión,
loelque
ledecir,
permite
diferente
a
nacional;
es
r

r
E
(
t
)



.
La
diferencia
restante
se
debe
a
que
el
sector
la
región
i
expansión,
lo
que
le
permite
crecer
a
una
tasa
diferente
a
como
lo
hace
en
el
resto
del
r
*
(

E
(
t

m
,
t
))
r

r
E
(
t
)


y
el
estándar
(
)
se
debe
a
que
el
sector

i ha

.
La
diferencia
restante
se
debe
a
sector
enha
la rc
icrecido
contradoha
unas
condiciones
económicas
específicas
que
facilitan
(o
dificultan)
su
i
i
ij
i
ij ai como
i
i el resto
isistema regional
encontrado
unas
condiciones
económicas
específicas
que
(o dificultan)
. que
mite crecer
a una
tasa diferente
loij hace
en
del facilitan
rij ri su
*
*
*
*
rij sido
r(o
dinámico
que
lahecho
media
rresto
 hace
r* .del
sión, lo que
le permite
crecer
ari una
tasa
diferente
como
loha
hace
eleconómicas
rijlepermite
sistema
regional
.
i . dificu
i lo
ha
encontrado
unas
condiciones
económicas
específicas
que
facilitan
(oen
dificultan)
su
expansión,
lo que
crecer
a una
diferente
a en
como
el sistema
resto del
diferente
a atasa
como
lo
el
conjunto
nacional;
esregional
decir,
ha
más
ha
encontrado
unas
condiciones
específicas
que
facilitan
*
r
*
j
*
*
*
expansión,
lo
que
le
permite
crecer
a
una
tasa
diferente
a
como
lo
hace
en
el
resto
del
rij La
 rdescomposición
ma regional
.La descomposición
expansión,
lo
que
le
permite
crecer
a
una
tasa
diferente
a
como
lo
hace
en
el r
r

r
E
(
t
)


dedinámico
(3)
puede
utilizarse
también
para
explicar
la
variación
del
empleo

.
La
diferencia
restante
se
debe
a
que
el
sec
rijLa descomposición
ri . de (3)
que
la
media
.
r

r
sistema
de
(3)
puede
utilizarse
también
para
explicar
la
variación
del
i regional
puede utilizarse itambién
i
iexplicar la variación del
*
iij para
*
*
La
descomposición
de
(3)
puede
utilizarse
también
para
explicar
la
variación
del
r

r
sistema
regional
.
r
*
j
S
empleo
regional
total,
sin
más
que
acumular
para
los
sectores:
regional
total,
sin
más
que
acumular
para
los
S
sectores:
r

r
sistema
regional
.
empleo regional total,
sin
para
ij
i más que acumular
unas
condiciones
económicas
quei facili
 riencontrado
Eijij(t )los
i S . sectores:
 ri ha
La diferencia
restante
se debe específicas
a que el sector
en l
empleo regional total, sin más que acumular
para
los loSi que
sectores:
expansión,
le permite crecer a una tasa3diferente a como lo h
ha
encontrado
unas
condiciones
económicas
específicas que facilitan (o dif
S
S
S
S S
* SS
* S *
*
E r * 
E r*
E* (tr)lo
Eque
r
 r* rrijEij 
(rtri)*i*.E
r3ijtasa
 ri* diferente
Eij (t )  3 a como lo hace en e
regional
Erir  Si 1 E
(
t
)


(
t
)



i
ij
le
permite
crecer
a
una
Si 1i 1Eij (ijt ) expansión,
Si i11 r*i ijsistema
S
*
ij ir** 
ij
ij
1
1
i
i


Ei  i 1 Eij r* i 1 Eij (t )  i 1 ri  r** Eij (t )  *i i11 rij  ri* Eij (t ) 
3
sistema regional rij  ri .









































































*
*
*
r
ij
r *r rE (rt*) E
ij
r*** Eij (t )  Si 1 rr**i*Eij r(**t*) E
(t )i 1 r
(t )i 1 ri  ri Eij (t )
i S
i 1 * ir ij *i
r* Eij (t )  i 1 ri  r* Eij (t )  i 1 ri  ri Eij (t )
S
S
S

















S




(4)
(4)
(4)
(4)
Esta última
expresión
la ecuación
básica Shift-Share.
del método Shift-Share.
Esta última expresión
constituye
la constituye
ecuación básica
del método
Esta
última
expresión
constituyelala ecuación
del método
Shift-Share.
Como la anterior
Esta
última
expresión
constituye
ecuaciónbásica
método
Shift-Share.
Como
la
anterior
de (3), el
descompone
elbásica
crecimiento
totalregional
del
empleo
regional en tres
Como
la anterior
de
(3),
descompone
crecimiento
total
deldel
empleo
en tres
de
(3),
descompone
el
crecimiento
total
del
empleo
regional
en
tres
factores:
Como
la anterior
de (3), descompone el crecimiento total del empleo regional en tres
factores:
factores:
factores: r * E (t )   j r * E (t )   j . Es el componente de crecimiento estándar en el empleo regional,
 ** ij
. Es* elij componente de crecimiento estándar en el empleo regional,
j
el componente
de
crecimiento
estándar
elempleo
empleo
regional,
Es
el
componente
crecimiento
estándar
enenel
regional,
común para
- r* Eij (t )   . Es
común
todasde
las
regionestambién
del
sistema,
también
denominado
común para todas
laspara
regiones
del
sistema,
denominado
National
Shift National Shift
común
para
todas
las
regiones
del
sistema,
también
denominado
National
Shift
o Impulso
nacional.
todas
las regiones
del sistema,
también denominado National Shift o Impulso nacional.
o Impulso
nacional.
S
S
o Impulso
*j
*
* nacional.
*
crecimiento
del empleo
regional
atribuible a la
r* Eij (t )el
 j . Define el
del
empleoregional
regional
atribuible
(t )i 
rij .Define
Define
el crecimiento
crecimiento
del
empleo
atribuible
a alalaestructura
- Si 1 r*i  r** Eij
1
 i 1 ri  r* Eij (t )   . Define el crecimiento del empleo regional atribuible a la
estructura
económica
existente
en
Es región
decir, se
sienlasectores
región se
estructura existente
económica
endecir,
la región
Es
decir, rsi. especializada
la
r . la
económica
en laexistente
región
r. Es
si la región
se región
encuentra
*
estructura
económica
en la
Es decir,
lar * 
región
se ( r *  r * ) , será
ra. nivel
encuentraexistente
especializada
enregión
sectores
dinámicos
asi nivel
nacional
encuentra
especializada
en
sectores
dinámicos
nacional
,
será
(
r
)
*
*
*
i
*
i
en
el empleo. Recidinámicos a nivel nacional (ri r* ), será más fácil que produzcan aumentos
encuentra especializada
en sectores
dinámicos
a nivel
nacional
(Recibe
ri*  r** ) ,laserá
más
fácil
que
produzcan
aumentos
en
el
empleo.
denominación
de
más fácil que produzcan aumentos en el empleo. Recibe la denominación de
be la denominación
de Industrial-Mix
o en
efecto
sectorial
comparado.
más
fácil
que
produzcan
aumentos
el
empleo.
Recibe
la
denominación
de
Industrial-Mix
o
efecto
sectorial
comparado.
Industrial-Mix o efecto sectorial comparado.
S
S
Industrial-Mix
o efecto
r sectorial
ri* Eijdos
(t )comparado.
componentes
 j . LosCiencias
dos componentes
se corresponden
con
(t )i 1 rjij .Los
 Si 1 rri r  r*i* Eij
anteriores
se anteriores
corresponden
Económicas 31-No.
2: 2013 / 135-156 /con
ISSN: 0252-9521
 i 1 ri  ri Eij (t )   . Los dos componentes anteriores se corresponden con
factores deestándar;
crecimiento
embargo,
cada
sector
en cada región
factores de crecimiento
sin estándar;
embargo, sin
cada
sector en
cada
región
factores
crecimiento
estándar;
sin embargo,
cadadesector
en cada región
crecediferente
de manera
diferente
las
deque
localización que
crece dedemanera
en función
deenlasfunción
facilidades
defacilidades
localización
crece
de manera
diferente
en
las facilidades
de denominación
localización
en Este
el función
territorio.
Este
factor
diferencial
recibe la que
denominación
de
encuentra
en encuentra
el territorio.
factor de
diferencial
recibe
la
de

o Impulso nacional.
o Impulso
nacional.
S
 Si 1 r*i*  r** Eij (t )   j j . Define el crecimiento del empleo regional atribuible a la
 i 1 ri  r* Eij (t )   . Define el crecimiento del empleo regional atribuible a la
estructura económica existente en la región r . Es decir, si la región se
estructura económica existente en la región r . Es decir, si la* región
se
encuentra especializada en sectores dinámicos a nivel nacional ( r  r * ) , será
encuentra especializada en sectores dinámicos a nivel nacional ( ri*i  r** ) , será
Rafael
Arias Ramírez
y Leonardo Sánchez
138 más fácil que produzcan aumentos en el empleo.
Recibe
la denominación
de Hernández
más
fácil que produzcan
aumentos
en el empleo. Recibe la denominación de
Industrial-Mix
o efecto sectorial
comparado.
Industrial-Mix
o efectoj sectorial comparado.
S
r
*
componentes
anteriores
se corresponden
con de cre- Si 1 rri  r*i Eij (t )  j . Los
Los dos
dos componentes
anteriores
se corresponden
con factores
 i 1 ri  ri Eij (t )   . Los dos componentes anteriores se corresponden con
factores estándar;
de crecimiento
estándar;
sin embargo,
cadacrece
sector
en cada
regiónen función
cimiento
sin embargo,
cada sector
en cada región
de manera
diferente
factores
demanera
crecimiento
estándar;
sin embargo,
cada sector
en cada región
crece
de
diferente
en
función
de
las
facilidades
de
localización
que recibe la
de las de
facilidades dediferente
localización
encuentralas
en facilidades
el territorio.de
Este
factor diferencial
crece
en que
función
localización
que
encuentramanera
en el territorio. Este
factor de
diferencial
recibe la denominación
de
encuentra
en de
el Regional-Share
Esteo efecto
factor
diferencial
recibe la denominación de
denominación
regional
comparado.
Regional-Share
oterritorio.
efecto regional
comparado.
Regional-Share o efecto regional comparado.
Por último, a la diferencia Ej j  j j se le denomina Shift-Net o crecimiento
Por último,
a laa la
diferencia
denomina
Shift-Net
o crecimiento
Por último,
diferencia E   se
se leledenomina
Shift-Net
o crecimiento
regional neto.
regional neto.
El empleo
homotético
en el sector
i de la
región
r se define
“el empleo que
El
Shift
Share
clásico
ha
sido
objeto
de
varias
críticas,
entre
ellas
la
incapacidad
para como
separar
regional neto.
el
sector
i
de
la
región
r
podría
tener
si
la
estructura
del
empleo
en
tal
región
el efecto sectorial comparado del efecto competitivo, lo cual se debe a que el análisis Shift-Share no fuera igual
a la objeto
estructura
nacional”
(Esteban-Marquillas,
p. 251). La incorporación del
El Shift Share
clásico
ha sido
deregional,
varias
críticas,
entre
ellas
la 1972,
incapacidad
considera
los efectos
multiplicadores
al nivel
de formaentre
que una
región
crecerá más, no únicaShift Share
clásico
ha sido
objeto
de del
varias
la incapacidad
empleo
homotético
encríticas,
elcompetitivo,
esquema ellas
básico
delseShift-Share
eliminar la
para El
separar
el
efecto
sectorial
comparado
efecto
lo
cual
debe
a conpermite
mente a causa
de sussectorial
ventajasinterrelación
competitivas,
sinoel
también
a causa de
unos
mejores
vínculos
otras
para
separar
el
efecto
comparado
del
efecto
competitivo,
lo
cual
se
debe
a
entre
efecto
sectorial
y
el
regional;
ya
que
permite
obtener
un efecto
que el análisis Shift-Share no considera los efectos multiplicadores al nivel regional, de
en la misma no
región.
Tal y como
plantea
Rosenfeld
(1959), el El
efectoregional,
competitivo
que
elindustrias
análisis
Shift-Share
considera
efectos
multiplicadores
de noserecoge
competitivo
libre
de esta
interdependencia.
homotético
denota como:
forma
que una
región crecerá
más,los
no
únicamente
a causaal nivel
de empleo
sus ventajas
exactamente
el especialcrecerá
dinamismo de unnosector
en una región
determinada,
sino que
va a estar influiforma
que una
únicamente
a causa
de industrias
sus
ventajas
competitivas,
sinoregión
también a causamás,
de unosR mejores
vínculos
con otras
en la
S
da por el efecto
sectorial ao causa
industry-mix,
pudiendo
originar
unacon
infraestimación
de dicho
efecto.
competitivas,
sino
también
de
unos
mejores
vínculos
otras
industrias
en
la
misma región. Tal y como plantea Rosenfeld
(1959),
el
efecto
competitivo
no
recoge
Eij
Eij R


(5)
S esta mezcla
La importancia
concedida
a
de
efectos
comentada
en
la
crítica
anterior
ha dado
misma
región.
Tal
y
como
plantea
Rosenfeld
(1959),
el
efecto
competitivo
no
recoge
1
exactamente el especial dinamismo
deE unj sector
enj 1 una 
región
determinada, sino que
Eij con
en
Eij determinada,

ij S sector
Ren la identidad
S una
R
lugar a una
serie de extensiones
base
clásica,
tomando
como
referencia
el conexactamente
el
especial
dinamismo
de
un
región
sino
que
j 1
1
va a estar influida por el efecto i sectorial
industry-mix,
pudiendo originar una
Eoijo Esteban
Eij(1972)


cepto
de
“empleo
homotético”
introducido
por
para
separar
el
efecto
de
la
especialiva
a
estar
influida
por
el
efecto
sectorial
industry-mix,
pudiendo
originar
una
i 1 i 1
i 1 i 1
infraestimación de dicho efecto.
infraestimación
de dicho
efecto. o diferencial.
zación del efecto
competitivo




Cuando se introduce la ecuación (5) en la identidad Shift-Share (1) se obtiene la
La importancia concedidasiguiente
a estaecuación:
mezcla de efectos comentada en la crítica
La importancia
concedida
a esta
mezcla de efectos
en la clásica,
crítica
anterior
dado
lugar
a una
serie
de
extensiones
con basecomentada
en la identidad
1. haUna
aproximación
al empleo
homotético
*
*
*
* 

*
(6)
anterior
ha
dado
lugar
a
una
serie
de
extensiones
con
base
en
la
identidad
clásica,

E

r
E
(
t
)

r

r
E
(
t
)

r

r
E
(
t
)

E

E
r

r
* de
* homotético”
ij
ij “empleo
i
ij
ij
i introducido
ij
ij
ij ij Esteban
i
tomando como referencia el concepto
por
tomando
como
referencia
el concepto
de
“empleo
homotético”
introducido
por
Esteban
El iempleo
homotético
en el como
sector“el
i de
(1972) para
efecto
de en
la especialización
del efecto
o“el
diferencial.
empleo
encompetitivo
el
sector
de
laempleo
región
r seel define
em
Elseparar
empleo el
homotético
elEl
sector
i de homotético
la región
r se
define
como
que
sector
(1972) para separar el efecto deellasector
especialización
del
efecto
competitivo
o
diferencial.
el
sector
i
de
la
región
r
podría
tener
si
la
estf
En
la
ecuación
(6)
el
efecto
regional
del
análisis
clásico
se
descompone
en
dos
la región
r podría
tener
si“ellafuera
estructura
empleo
en tal región
de la región
r podría
si lahomotético
estructura
del el
empleo
eni de
tal
región
adel
lacomo
estructura
El iempleo
homotético
en
el sector
i dei de
la región
r se
define
como
empleo
que
Eltener
empleo
en
sector
la
región
r seigual
define
“el empleo
que
* 
a región
la
estructura
nacional”
(Esteban-Marquil
a lasi
la
(Esteban-Marquillas,
1972,
p.elregión
251).
La incorpor
(Esteban-Marquillas,
1972,
incorporación
del
empleo
homotético
esqueel sectornacional”
i de la región
relpodría
laestructura
estructura
empleo
en
tal
igual
rp.
Eij (La
tnacional”
)del
sectortener
i departes;
región
rripodría
tener
si la
estructura
delfuera
empleo
enen
tal
fuera
igual la
ij 251).
representa
el efecto
competitivo
netoShift-Share
(ECN),
el cual
mide
empleo
homotético
en
el
esquema
bási
empleo
homotético
en
el
esquema
básico
del
permite
a la estructura
1972,
p.
251).
La
incorporación
del
ma básiconacional”
del Shift-Share
permite
eliminar
la
interrelación
entre
el
efecto
sectorial
y
el
regional;
ya
a la (Esteban-Marquillas,
estructura
nacional”
(Esteban-Marquillas,
1972,
p.
251).
La
incorporación
del el
ventaja o homotético
desventaja competitiva de interrelación
la región j conentre
respecto
al sector
i de la nación.
el
efecto
sectorial
y
el
re
1
Una
aproximación
al
empleo
interrelación
entre
el
efecto
sectorial
y
el
regional;
ya
que
permite
obtener
empleo 1
homotético
en
elunesquema
básico
del esquema
permite
que
permite
obtener
efecto
competitivo
de
esta* interdependencia.
El empleolahomotético
empleo
en Elibre
el
básico
del eliminar
Shift-Share
permite seeliminar la
Shift-Share
Una
aproximación
alhomotético
empleo
homotético

E
r

r
competitivo
libre
de
esta
interdependencia.
ij
ij
ij
i
competitivo
libre
de
esta
interdependencia.
El
empleo
homotético
se
denota
cE
interrelación
sectorial
y elel
regional;
ya que permite
obtener
efecto
denotaentre
como:el efecto
Por
otro
lado,
efecto
“locacional”
(EL) y toma
cuenta
interrelación
entre
efecto sectorial
yeseldenominado
regional;
yaun
que
permite obtener
un en
efecto
3
el
grado
de la región
j en la producción
delse
sector
i . como:
competitivo libre de esta
interdependencia.
Elespecialización
empleo
homotético
se
como:
competitivo
libre
de de
esta
interdependencia.
El denota
empleo
homotético
denota












R
R
S
Eij   Eij
i 1
ij
j 1
R
 E
ij





  

E
E


 E   EE lo mismo con
E E

la magnitud
delEefecto, ya que la variable empleo E es sustituida por el
E
E
 E

 E (región posee misma
empleo homotético
estructura
de empleo
el país).
Cuando
se introduce
la que
ecuación
(5)En
en
E
ij
S

S
E
S
R
S
En el Modelo
Shift-Share
de Esteban-Marquillas
Eij (ME-M),
4 Eij se tiene que por
E
Eij Ren el signo
S
R
ij
(5)
4 j 1
R
S no hay diferencias
construcción
del j efecto
competitivo
con relación(5)
al
S
1

(5)
j 1
j 1

Eij  Eij S R
 S R
Eij*
E
E
E

E

E
(5)ij S Rya
(
r

r
)
ij que
análisis
clásico,
las
tasas
de
no
son
modificadas
.
No
pasa
ij ij
ij
S
R
(5)crecimiento
R
ij
i
i 1
j 1
S
j 1
R
ij
S R
i 1j 1
ij
ij ij S
j 1
R
i 1
S
ij
j 1
R
i 1 i 1
ij
ij
j 1

ij
i 1 i 1
j 1
ij
ij
i 1 i 1
ij
i 1 i 1 ij
ij
i 1 i 1se introduce
Cuando
la ecuación (5) en la identidad Shift-Share (1) se
cuanto
al
efecto
“locacional”,
se Shift-Share
pueden
presentar
posibles
resultados (Herzog
siguiente
se introduce
la
ecuación
(5)
en
la
identidad
(1)ecuación:
se cuatro
obtiene
la siguiente
siguiente
ecuación:
Cuando Cuando
se introduce
laCuando
ecuación
(5)
en
la
identidad
Shift-Share
obtiene
introduce
(5) en la(1)
identidad
Shift-Share
(1) seespecialización
obtiene la
& se
Olsen,
2001, la
p. ecuación
445), dependiendo
delsesigno
del la
componente
*
* * *
* 
siguienteecuación:
ecuación:
 *
siguiente ecuación:
* del* componente competitividad
*E  r E (t ) (
 r
*(
(6)

r
r
E
t
)

r

rresumen
E
(
EE

E
)
r

)
y
al
signo
,
los
cuales
se
ij i i *
ij
ij
* ij
ij
ij
ij
i Eij (t ) en
ij  r* Eij (t )  ri  r* Eij (t )  rij  ri Eij (t )  Eij  Eij rij  ri
*
*
*
*el siguiente
 *

** 
(6)
*
* cuadro:

*
(6)
E  r E (t)  r  r E(Et)  r E r(t)E (rt)rEE(E
(6)
t) rr rr E (t)  E  E r  r
i 1 i 1
ij
*
ij

i
i 1 i 1
*

ij
i 1 i 1
ij

*ij
ij i
  
ij i
 
 
* ij ij
ij


ijij
ii

ij


ij
ij


ij
i

    


En ladel
ecuación
el efecto
regional d
En la ecuación (6) el efecto regional
análisis(6)
clásico
se descompon
* 
*

r

r
E
(
t
)
En la ecuación
(6) el efecto
regional
del
análisis
clásico
se del
descompone
en
En la ecuación
(6)laelecuación
efecto regional
del análisis
clásico
se descompone
partes; en dos
En
el efecto
regional
análisis
se dos
descompone
ij clásico
i dos
ij en
r(6)
ij  ri Eij (t)
el efecto
partes;
representa partes;
el efecto competitivorepresenta
neto (ECN),
el cua
* 
* 
rij  ri Eij (t) representa rel
efecto
competitivo
neto
(ECN),
el
cual
mide
la
ventaja
o
desventaja

r
E
(
t
)
ventaja
o
desventaja
competitiva
de la i regió
ij el
i efecto
ij
ventaja
o
desventaja
competitiva
de
la
región
j
con
respecto
al
sector
de
partes;
representa
competitivo
neto
(ECN),
el
cual
mide
la
partes;
representa el efecto competitivo neto (ECN),
el* cual mide la

 la nación.
*al sector
de competitiva
la
región
j
con
respecto
al
sector
i
de
Por
otro
lado,
es
E

E
r

r
ventaja competitiva
o desventaja
de
la
región
j
con
respecto
i
de
la
nación.
ventaja o desventaja competitiva
j otro
con lado,
respectoij al sector
ij ij
ii de la nación.
Eij  Eij de
rij lari región
es(EL)
denominado
Por otro lado,
es Por
denominado
efecto “locacional”
y toma

*
toma en
* cuenta el grado
denominado
“locacional”
(EL)
y
de
especialización
de
la
región
j en
Eij  Eefecto
r

r
3
E

E
r

r
el
grado
de
especialización
de
la
región
ij ij
i
ij
ij
ij
i
el
grado
de
especialización
de
la
región
j
en
la
producción
del
sector
i
. j en
Por otro lado,
denominado efecto es
“locacional”
(EL)efecto
y toma“locacional”
en cuenta (EL) y toma en cuenta
Por otroes
lado,
denominado
3
3
delelsector
. región
el gradoladeproducción
especialización
deila
j en el
la producción
del sector
. En
el Modelo
Shift-Share
grado
de
especialización
de la región
j en laide
producción
del sector
i 3.(ME-M), dese Esteba
En
Modelo
Shift-Share
Esteban-Marquillas
tiene
construcción
no
hay
diferencias
en el sign
construcción
no hay diferencias
en tiene
el signo
delpor
efecto
En el Modelo Shift-Share
Esteban-Marquillas
se
que
En el de
Modelo
Shift-Share
de(ME-M),
Esteban-Marquillas
(ME-M),
secompetitivo
tiene que con
por re
3
análisis
clásico,
yaalen
que
lascon
tasas
de
crecimie
construcción
no
diferencias
en
el
signo
deleldelya
efecto
competitivo
conefecto
relación
Esta
relación
sediferencias
deriva
hecho
deen
que
el tasas
empleo
homotético
puede
ser expresado
en términos
de cociente
de localización,
3
Estahay
relación
se deriva del
hecho
de
que
empleo
homotético
puede
ser
expresado
términos
derelación
(rij alri* )
construcción
no
hay
el
signo
del
competitivo
análisis
clásico,
que
las
de
crecimiento
no
son
modificadas
*
*
E
cociente
deanálisis
localización,
. lasla
lo mismo
magnitud
ya
que
(rijno
 rison
) .con
análisis clásico,
ya que
las tasas
de
crecimiento
no
son de
modificadas
No
pasa
(rijdel
 riefecto,
)E. ijNo
clásico,
tasas
crecimiento
modificadas
. con
Eij mismo
 yaij que
lo
magnitud
del efecto,
ya
que
la la
variable
empleo
espasa
sustitu
CLij


lo mismo con la magnitud
del efecto,
que
la variable
esvariable
sustituida
por
el EEijij es
E ijposee
empleo
homotético
(región
posee
mism
lo mismo
con
layamagnitud
del efecto,
ya que
la
empleo
sustituida
por
elel
Eempleo
empleo
homotético
(región
misma
estructura
de
empleo
que












Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521

ij






5
efecto
se país).
pueden
empleo homotético Eijempleo
(regiónhomotético
posee
misma
estructura
de empleo
que al
elpresentar
país).
En
posee
misma
estructura
de “locacional”,
empleo
el
Enpre
cuanto
alEefecto
“locacional”,
se cuanto
pueden
cuatro que
posibles
resultado
ij (región
&
Olsen,
2001,
p.
445),
dependiendo
de
& Olsen,
2001, cuatro
p.
dependiendo
del(Herzog
signo del componente espec
cuanto al efecto “locacional”,
seefecto
pueden
presentar
posibles
resultados
cuanto al
“locacional”,
se 445),
pueden
presentar
cuatro posibles resultados (Herzog

*
(
E

E
)
y
al
signo(rdel
& Olsen, 2001, p. 445),
dependiendo
del
signo
del
componente
especialización
ij
ij
( E  Ep. ) 445),
 rcomponente
) ,especialización
& Olsen, 2001,
dependiendo
del signo
del componente
y al signo
del componente
competitividad
los cualescompe
se re
139
Análisis de la dinámica regional del empleo utilizando el modelo shift share...
En el Modelo Shift-Share de Esteban-Marquillas (ME-M), se tiene que por construcción no
hay diferencias en el signo del efecto competitivo con relación al análisis clásico, ya que las tasas
de crecimiento no son modificadas (rij - ri ). No pasa lo mismo con la magnitud del efecto, ya que
la variable empleo Eij es sustituida por el empleo homotético E�ij (región posee misma estructura de
empleo que el país). En cuanto al efecto “locacional”, se pueden presentar cuatro posibles resultados
(Herzog & Olsen, 2001, p. 445), dependiendo del signo del componente especialización (Eij - E�ij) y al
signo del componente competitividad (rij - ri* ), los cuales se resumen en el siguiente cuadro:
CUADRO 1
MODELO SHIFT-SHARE ESTEBAN-MARQUILLAS: POSIBLES RESULTADOS
DEL EFECTO “LOCACIONAL”
Efecto “Locacional” (EL)
Especialización
Eij - E�ij
Competitividad
(rij - ri )
1 Desventaja Competitiva,
Especialización
-
+
-
2 Desventaja Competitiva, Sin
Especialización
+
-
-
3 Ventaja Competitiva, Sin
Especialización
-
-
+
4 Ventaja Competitiva,
Especialización
+
+
+
Fuente: Herzog & Olsen, 2001.
El efecto “locacional” muestra si una región se especializa, (Eij - E�ij ) > 0, en aquellos sectores
donde disfruta de ventaja competitiva (rij - ri* ) > 0. Además, el elemento competitividad (rij - ri* ) del
efecto “locacional” es el mismo que el efecto competitivo neto, por lo que es de esperar que estos dos
componentes tengan el mismo signo. No obstante, la introducción del empleo homotético soluciona
únicamente el problema de la interdependencia de los efectos y no la interdependencia espacial; para
ello se hace necesaria la introducción de la matriz de pesos espaciales.
2.
Introducción de la matriz de pesos espaciales y auto-correlación espacial
Como se mencionó anteriormente, el análisis clásico considera a las unidades de análisis (regiones) como realidades independientes. Este supuesto entra en contradicción con la ley de geografía de
Tobler, la cual afirma que “todo está relacionado con todo, siendo esta relación más fuerte en aquellas
cosas que se encuentran más cerca” (Toral, 2001, p.101). Mayor & López (2005, p.7) afirman que una
región no debe ser considerada una realidad aislada de los territorios que la rodean, sino que la estructura económica de cada unidad espacial dependerá en mayor medida de aquellas regiones consideradas
“vecinas”. Lo cual supone la existencia de un cierto grado de auto-correlación espacial.
De acuerdo con Cliff y Ord, la auto-correlación espacial es la “característica según la cual la
presencia de una determinada cantidad o calidad de la variable estudiada en una determinada zona
o región haga más o menos probable su presencia en las zonas o regiones vecinas” (1973, como se
cita en Toral, 2001, p. 101). En nuestro caso, el índice de Moran (I), que es una prueba de auto-correlación, permite verificar si el empleo observado en una región j es independiente de los valores del
empleo observado en las regiones vecinas.
Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521
acuerdo
con
Cliff
Ord,
auto-correlación
la “cara
acuerdo
con
Cliff
yla Ord,
la auto-correlación
espacial
es
acuerdo
conDe
Cliff
y Ord,
lay auto-correlación
espacial
es
la “característica
en lasDe
zonas
oDe
regiones
vecinas”
(1973,
como
se cita
en
Toral,espacial
2001,
p.es101).
En
según
la
cual
la
presencia
de
una
determinada
cantidad
o
calidad
de
según
la
cual
la
presencia
de
una
determinada
cantidad
o
calida
según
la
cual
la
presencia
de
una
determinada
cantidad
o
calidad
de
la
variable
nuestro caso, el índice de Moran (I), que es una prueba de auto-correlación, permitela
enobservado
una determinada
zona
o región
más
oprobable
menos
su
en una
zona
ohaga
región
haga
más
o probable
menos
proba
estudiada
enempleo
unaestudiada
determinada
zona
o región
haga
o menos
su
presencia
verificar
siestudiada
el
endeterminada
una
región
j esmás
independiente
de los
valores
del
en
las
zonas
o
regiones
vecinas”
(1973,
como
se
cita
en
Toral,
2001,
o regiones
cita en
Toral,p.
2
en las observado
zonas o en
regiones
vecinas”
(1973, vecinas”
como se (1973,
cita encomo
Toral,se2001,
p. 101).
En
empleo
enlas
las zonas
regiones
vecinas.
nuestro
caso,
el
índice
de
Moran
(I),
que
es
una
prueba
de
auto-correlación
caso,
el índice
dees
Moran
(I), quede
es auto-correlación,
una prueba de auto-co
nuestro caso, el nuestro
índice de
Moran
(I), que
una prueba
permite
Una si
matriz
de
seen
puede
construir
utilizando
criterios.
Para
Rafael
Arias
Ramírez
yregión
Leonardo
Sánchez
140
verificar
sicontigüidad
el observado
empleo
observado
en
unaj en
esdiferentes
independiente
de los
va
verificar
si el empleo
observado
una j región
jHernández
esdeindependiente
d
verificar
el empleo
una
región
es
independiente
los valores
de
elempleo
cálculoobservado
de la I empleo
deenMoran
se
utiliza
una
matriz
booleana
W
basada
en
criterios
de
empleo
observado
en
las
regiones
vecinas.
en las regiones vecinas.
lasobservado
regiones vecinas.
Talseque
el construir
valor de utilizando
doscriterios.
regionesPara
comparten
una frontera
wij es 1 cuando
Una matrizadyacencia.
de contigüidad
puede
diferentes
el cálculo
Una
contigüidad
se
puede
utilizando
diferentes
crite
Unade
matriz
depuede
contigüidad
seconstruir
puede construir
utilizando
diferent
Una matriz
dematriz
contigüidad
se
construir
utilizando
diferentes
criterios.
Para
común,
y
cero
en
caso
contrario.
Los
elementos
de
la
diagonal
principal
son
nulos.
de la I de Moran se el
utiliza
una
matriz
booleana
W
basada
en
criterios
de
adyacencia.
Tal
que
el
valor
el
cálculo
de
la
I
de
Moran
se
utiliza
una
matriz
booleana
W
basada
en
cr
cálculo
I de Moran
se utiliza
una matriz
booleana
W basad
cálculo de la el
I de
Morandeselautiliza
una matriz
booleana
W basada
en criterios
de
de wij es 1 cuando adyacencia.
dos regiones
comparten
una
frontera
común,
y
cero
en
caso
contrario.
Los
eleadyacencia.
Tal
que
el
valor
de
es
1
cuando
dos
regiones
comparten
un
w
Tal
que
el
valor
es
1
cuando
dos
regiones
compa
w
ij de dos
que
el
valor
de
es
1
cuando
regiones
comparten
una
frontera
w

w
 0 Talwadyacencia.

ij
ij
12
1N
mentos de la diagonal principal
son nulos.
casoen
ycaso
cero
en
contrario.
Los elementos
de la diagonal
principal
son n
y cero
caso
contrario.
Los
elementos
de la diagonal
princip
w21 en0común,
 w
común, ycomún,
cero
contrario.
Los
elementos
de
la diagonal
principal
son nulos.
2N 
W
 0
w  0 w
 w120  w
w1N   w 
12
1N
12
1N






w
w

0
w
w
0

N1
N0
2  21
 w

w
0

w
2
N

w

21
2N 
W   21 W    W 2 N  
   dada
 por:
 Moran para
  t viene
 un
  año
La I de






0
w
w

w
w

0
N
1
N
2


w
w

0
n
N2
  N1

N2 n
 N1
W

jk ( x jt  xt )( xkt  xt )
La I de Moran para un añont La
viene
dada
por:
I de
Moran
para
un para
añodada
tun
viene
por:
I deaño
Moran
año
t viene
dada por:
La I de Moran
t viene
por:dada
para
1 La
1 un
It  n n
*j k
(7)
n
n
n
n
n
n
2 n
W jk
xt )(( xxktjt  xxtt ))( xkt  xt )


t ))(
jk
W jk((x
xjtjtxxW
x(ktx jtxW

t
t )jk
j 1 k 1
nI  j 1nk 1 j 1* j n1 k 1 j 1 k 1
(7)
*n
t
(7) (7)
It 
*n nI t  nn n
(7)
n
2
Donde:n n
2
2 (x  x )
W
jt
t ( x jt  xt )
W jk  jk
 ( x jtWjkx
t)
nj 1 k 1
j 1 k 1
j 1
jj11 k 1
j 1
x jt

Donde: Donde:
Donde:
Donde:
j 1
(8)
xt 
n
n
nn
x jt  x jt

x jt

j 1 del logaritmo
Esta es
media
natural (neperiano)
del empleo xit , en la región i, y
1
j 1 la x
(8)

(8)
xt  j
(8)
t
(8)
xt 
n
W jk es la matriz
n
n binaria de contigüidad.
xregión
Esta
es del
la
logaritmo
natural
Esta es la media La
del
logaritmo
natural
(neperiano)
del
empleo
xit , en(neperiano)
laadel
región
i, ydel
Wjk
esen
la
Esta
es ladel
media
del
logaritmo
natural
(neperiano)
della
empleo
it , en la
xempleo
Esta
es la
media
delmedia
logaritmo
natural
(neperiano)
i,xi
interpretación
Índice
de
Morán
es
análoga
un empleo
coeficiente
correlación
it , de
matriz binaria de contigüidad.
matriz
de
contigüidad.
W jk esyala
convencional,
que
su
numerador
sedeinterpreta
como la covarianza de unidades
labinaria
matriz
binaria
contigüidad.
W
binaria
contigüidad.
W jk es la matriz
jk es de
La interpretación
del Índice
de Morán
análoga
a unentre
coeficiente
de correlación
convencioespaciales
contiguas
y suesvalor
oscila
-1 (cuando
existe una
fuerte correlación
La
interpretación
del
Índice
de
Morán
es
análoga
a un coeficiente
de co
nal, ya que su numerador
se
interpreta
como
la
covarianza
de
unidades
espaciales
contiguas
y su
La
interpretación
del
Índice
de
Morán
es
análoga
adeuncorrelación
coeficien
La
interpretación
del
Índice
de
Morán
es
análoga
a
un
coeficiente
negativa) y 1 (cuando existe una fuerte correlación positiva).
ya numerador
que ya
su que
numerador
interpreta
covarianza
de
valor oscila entre -1convencional,
(cuandoconvencional,
existeya
una
fuerte
correlación
negativa)
yse
1 (cuando
una la
fuerte
convencional,
numerador
se existe
interpreta
como
covaria
que
su
sesu interpreta
como
la como
covarianza
delaunidades
Con espaciales
la contiguas
finalidad
de
determinar
la ysignificancia
estadística
lafuerte
I deuna
Moran,
secf
contiguas
y su
valor
-1entre
(cuando
existe
fuerte
espaciales
contiguas
suoscila
valor
oscila
-1de
(cuando
existe
una
correlación positiva).
espaciales
y su
valor
oscila
entre
-1 entre
(cuando
existe
una
correlación
calcula
un
estadístico
z(I)
bajo
el
supuesto
de
aleatoriedad
en
el
cálculo
del
primer
y
negativa)
y
1
(cuando
existe
una
fuerte
correlación
positiva).
y 1una
(cuando
fuerte
positiva).
negativa)
y 1 (cuando
existe
fuerteexiste
correlación
positiva).
Con la finalidad
de determinar
lanegativa)
significancia
estadística
de la I una
de Moran,
secorrelación
calcula un estadíssegundo momento de la I de Moran. La normalidad de este estadístico “depende del
tico z(I) bajo el supuesto de
aleatoriedad
el
cálculo
del
ysignificancia
segundo
momento
de laestadística
I de
Con en
la considerados
finalidad
deprimer
determinar
la significancia
deMoran,
la de
I de
dela
M
Con
la finalidad
de
determinar
la conectados,
significancia
estadística
la
Con
finalidad
de
determinar
estadística
deMoran.
laes
I de
se
número
de lavínculos
y lade
cómo
están
decir,
La normalidad de este
estadístico
“depende
del
número
de
vínculos
considerados
y
de
cómo
están
calcula
un
estadístico
z(I)
bajo
el
supuesto
de
aleatoriedad
en
el
cálculo
de
calcula
un
estadístico
z(I)
bajo
el
supuesto
de
aleatoriedad
en
el
cál
calcula
un
estadístico
z(I)
bajo
el
supuesto
de
aleatoriedad
en
el
cálculo
del
primer
y
estructura de la matriz de pesos espaciales (Mayor & López, 2005, p. 16)
conectados, es decir,segundo
de la estructura
desegundo
la
matriz
de
pesos
López,
2005,
16) de
segundo
momento
de
la espaciales
I de
Moran.
La &
normalidad
dep. este
estadístico
“dep
deLa
la normalidad
I (Mayor
de Moran.
Laeste
normalidad
este
estadíst
momento
de
la Imomento
de
Moran.
de
estadístico
“depende
de
de
Iconsiderados
depor:
Moran
viene
dada
por:
número
deladada
vínculos
considerados
y deestán
cómo
están
La varianza de
la La
I devarianza
Moran
viene
número
de
vínculos
y de
cómo conectados,
están
número
de vínculos
y considerados
de cómo
conectados,
es conectados,
decir,esdedec
la
estructura
de
la
matriz
de
pesos
espaciales
(Mayor
&
López,
2005,
p.2005,
16) p.
estructura
de
la
matriz
de
pesos
espaciales
(Mayor
&
López,
estructura de la matriz
de
pesos
espaciales
(Mayor
&
López,
2005,
p.
16)

1 Donde:
2
(n 2de
VarN ( I )  La2 varianza
S1 lanS
 3Moran
S02 )   E
(9)
N ( I ) dada por: (9)
2
I 2de
viene
La
varianza
de
la
I
de
Moran
viene dada por:
La varianza
de
la
I
de
Moran
viene
dada
por:
(
1)
S
n

 0

n
Donde:
n
SDonde:
1Wij
0  
 ( I1Donde:
 2 3S 2 )2  E (10)
2 2
2
)   iN(n12(2IjS)12nS(n21S31S2 )nS
) 2  3NS(0 I))  E(9)
VarN ( I ) Var
N (I )
 N2 2 Var
(n2 ES1N ( I0nS
n
n
1
0
2
2
(
1)
S
n

n
n
S0 (n  1)
 0


 S0 (nS01)
WW
(10)
ijde la matriz de pesos espaciales.
(10)
esS la
suma

0
n
n
i 1i 1j 1j 1
ij
eseslala(suma
de
es la suma de la matriz de pesos espaciales.
Wsuma
) 2lalamatriz

ij  W
jide
matrizdedepesos
pesosespaciales.
espaciales.
i 1 j 1
n nn n
(11)
W ji ) 2 ) 2

ij 
(W(2W
ij  W
ji
i 1i 1j 1j 1
(11)
(11)
22
n
(12)
S 2   (Wi  W j ) 2
i 1
n n
(9)
(9)
(10)
7
(11)
(12)
2 2
Mientras que la desviación típica yMientras
valores
correspondientes
a unay(12)
distribución
Slos
(Wique
 z(I)
W j )la

desviación típica
los valoresnorz(I) correspon
2S
(12)
2   (W
i W
j)
i 1i 1
mal estándar vienen dados por:
distribución normal estándar vienen dados por:
Mientras
que
desviación típica
Mientras
quela
típicay(13)
ylos
losvalores
valoresz(I)
z(I)correspon
correspo
DT
 Var
( Ila
) desviación
Ciencias Económicas 31-No. 2: 2013 / 135-156
/ ISSN:
0252-9521
N ( I )normal
N
distribución
estándar
vienen
dados
por:
distribución normal estándar vienen dados por:
I ) N ( I )
 I  E) N (Var
(13)
DT
N (NI()I
(13)
DT
VarN ( I )
z
(14)
Var ( I )
ij
ji
2
S 2   (Wi  W j ) 2
(11)
n
(Wi  W j ) 2
(12)
i 1
n
2
2
(12) (12)
S 2  S
(Wi  W j )que
Mientras
la desviación típica
y los valores z(I) correspo
2   (Wi  W j )
i 1

1
i
distribución normal estándar vienen dados por:
(12)
Mientras
que shift
la share...
desviación típicatípica
y losy valores
z(I)141z(I)
correspondie
Análisis de la dinámica regional del empleo utilizando
el modelo
Mientras
que
los valores
correspo
(13)
DT
VarNla( I )desviación
N ( I ) estándar
distribución
normal
vienen
dados
por: por:
distribución
normal estándar
vienen
dados
s que la desviación típica y los valores z(I) correspondientes a una
 EN((II)) 
normal estándar vienen dados por:
DTN (DT
Iz)(II)Var
 N Var ( I )
N
VarN ( I )
I E
( IE)  ( I ) 

N
I

N
z z
VarN Var
(I ) (I )
(13)
 VarN ( I )
EN ( I ) 
(14)
arN ( I )
3.
(13) (13)
(14)
N
(14) (14)
(13)
(14)
N
3 Incorporación del Shift-Share Espacialmente Modificado (
Este modelo
incorpora
variación del concepto de em
Incorporación del Shift-Share 3Espacialmente
Modificado
(MME) una Espacialmente
Incorporación
del Shift-Share
Modificado (MME
3(MME)
Incorporación
Shift-Share
Espacialmente
Modificado
(M
propuesto
por Esteban-del
Marquillas,
referido
a un ámbito
más próxim
orporación del Shift-Share Espacialmente Modificado
empleo homotético respecto a las regiones vecinas puede definirse
modelo
incorpora
una
variación
del del
concepto
Estevariación
modelo incorpora
una variación
del concepto
de
empleo
homotético
propuesto
por
Este-de empleo
Este
modelo
incorpora
una
variación
concepto
de emp
modelo incorpora una
del concepto
deEste
empleo
homotético
en
el
sector
i
de
la
región
j
si
la
estructural
sectorial
de
región
coin
propuesto
por
EstebanMarquillas,
referido
a
un
ámbito
más
próximo
a l
banMarquillas,
referido
a
un
ámbito
más
próximo
a
la
región.
El
empleo
homotético
respecto
a esa
lasmás
or Esteban- Marquillas, referido a un ámbito más propuesto
próximo a lapor
región.
El
EstebanMarquillas, referido a un ámbito
próximo
su
entorno
o
grupo
de
regiones
vecinas”
(Mayor
&
López,
2005,
p.13).
empleo
homotético
respecto
a
las
regiones
vecinas
puede
definirse
como
otético respecto
a las regiones
vecinas
puede
definirse
como
“el
empleo
regiones
vecinas puede
definirse
como
“el
empleo
en
el
sector
i
de
la
región
j
si
la
estructural
secempleo homotético respecto a las regiones vecinas puede definirse c
elen
ientorno
de la
región
j sidelaj regiones
estructural
sectorial
de &
esa
región
coincidies
de la región jtorial
si la estructural
sectorial
de esaen
región
coincidiese
lagrupo
de
de esa región
coincidiese
con
lasector
de
ola
vecinas”
(Mayor
López,
el su
sector
i con
de
región
si
la estructural
sectorial
de
esa región
coinc
grupo de regiones
(Mayor & López, 2005,
p.13).
Donde:
su entorno
o grupo
de regiones
vecinas”
(Mayor
& López,
2005,
p.13).
DondD
2005,vecinas”
p.13). Donde:
su
entorno
oS grupo
deEikregiones
vecinas”
(Mayor
& López,
2005,
p.13).

Eijv   Eij Skv
Eik

i 1
E

ik
S
 EikEik
S
v
k v
 Eij Skv
ik1v kv
v E
Eij  E
 ij SEij S
(15)
Eik

(15) i ij1 
1
i 
Eik E
i 1 kv

ik
i 1 kv
i 1 kuna
v
No obstante,
opción más elaborada es la utilización de m
(15)elaborada
(15)
No obstante,
más
es latal
utilización
espaciales
que:
tante, una opción más
elaboradauna
es opción
la utilización
de matrices
de
pesos de matrices de pesos espaciales tal que:
al que:
No obstante,
una una
opción
másmás
elaborada
es laesutilización
de matrice
No v*obstante,
opción
elaborada
la utilización
de ma
(16)
E

w
E
espaciales
tal
que:

ij
ij
ik
espaciales tal que:
w E
ij
k (16)
v
ik
v* w E
E EEsto
supone
utilizar un empleo espacialmente modificado en

ikw E
 ij
v
v*
ij
Esto supone
utilizar modificado
un empleoen
espacialmente
modificado en función de una matriz de
ij
ij ik
upone utilizar un empleo
espacialmente
función
de
una
v
k v
matrizkde
pesos
W, en lugar de una variación del empleo homotético
sos W, en lugar
deW,
una
homotético.
Nohomotético.
obstante la No obstante la definición (16) plantea
pesos
envariación
lugar de del
unaempleo
variación
del empleo
el
S
R
S
R
EstoEsto
supone
utilizar
un empleo
espacialmente
modificado
en func
v*
supone
utilizar
un empleo
espacialmente
modificado
en


matriz
de
pesos
W,
en
lugar
de
una
variación
del
empleo
homotético
i 1 j 1
i 1 j 1
i 1 j 1
i 1 j 1
S
R
S
R
S v*R
S
R
connolas
magnitudes
Para
solucionar
este
problema
se de
utilizan
ponderaciones
del empleo
espacialmente
modificado
no
coincide
con
las
magnitudes
espacialmentecoincide
modificado
coincide
con lasoriginales.
magnitudes
originales.
Para
v*
E

E
definición
(16)
plantea
el
inconveniente
que

ij
ij , es de
E
definición (16) plantea el inconveniente de que

ij   Eij , e
este problema
se
utilizan
ponderaciones
sectoriales
modificadas
solucionar
estecomo:
problema se utilizan i ponderaciones
sectoria
1 j 1
i 1 j 1
sectoriales modificadas espacialmente,
que se calculan
i 1 j 1
i 1 j 1
te, que se calculan como:
R
espacialmente,
que
se
calculan
como:
del empleo
espacialmente
modificado
no
coincide
con
las
magnitudes
orig
del empleo espacialmente
modificado no coincide con las magnitudes
*
Eijvproblema

solucionar
este
se
utilizan
ponderaciones
sectoriales
R
v
*
solucionar j 1 veste
problema
Ei R v* se utilizan ponderaciones sectoriale
*
Eque
espacialmente,
secalculan
8 v* 

ij
Eij como:
v*se
espacialmente,
que
calculan
como:
S
R
R
j 1
Eiv*
v* Ei E j 1
(17)
v*

E
E

ij

ij
S 
R
v* S R
v*
v*
E
E
E
*
v
v
*
i 1 j 1
j 1
Eij
Eij

 iv*
(17)

S
R
i 1 j 1
E
i 1 j 1
v*
Tal
que:
E
 ij
Tal que:
Tal que: i 1 j 1
Tal que:
Eiv*
v**

E
E
(18)
E v* (18)
* v*
ij
Tal que:
Ej ivE
(18)
Eijv**  E j iv*
v**
Eij  E j v*
E(18)
E que guarda cierta relación con la ecuación (15), p
Eiv*
v**
Ecuación
(18)
E

E
Ecuación
queenguarda
cierta
relación
Ecuación que
guarda
cierta relación con la ecuación
(15), pues
lugar de
utilizar
datoscon
del la ecuación
ij
j
utilizar
datos utilizar
del empleo
de empleo
lasrelación
regiones
vecinas,
utiliza (15),
el
emple
E v*
Ecuación
que
guarda
cierta
la ecuación
pu
datos del
de lascon
regiones
vecinas,
utiliza
el
modificado
en
función
de
la
matriz
de
vecindad.
Gracias
a
esta
varian
empleo de las regiones
vecinas,
utiliza
el
empleo
espacialmente
modificado
en
función
de
la
matriz
utilizar
datos
del
empleo
de
las
regiones
vecinas,
utiliza
el
empleo
modificado
en
función
de
la
matriz
de
vecindad.
Gracias
a
esta
Ecuación que guardaS cierta
relación
con laS ecuación
(15), pues en lugar de
R
SR R
R
modificado
en Sfunción
de la matriz
deelvecindad.
Gracias a esta variante
v**regiones
v**
utilizar
datos
delvariante
empleo
de
las
vecinas,
utiliza
empleo
espacialmente
E

E
,
al
introducir
ensustisustitución
del em
E

E
,
al
introducir
(18)
en sustitución
del empleo
al
introducir
(18)
en
de vecindad.
Gracias
a esta
se
cumple
que

ij
ij
S 
R
S 
Rij ij

1

1

1

1
i
j
i
j
v
**
modificado en función de lai 1matriz
de
vecindad.
Gracias
a
esta
variante
se
cumple
que
j 1
i 1 j 1
E

E

ij
ij , al introducir (18) en sustitución del empleo ho
R
S
R
ecuación
(6),
se tiene
ecuación
delShift-Share
Modelo
Shift-Share
Espa
tución del Sempleo
homotético
de la 
(6),(6),
tiene
la ecuación
del la
Modelo
Shift-Share
Espatiene
la ecuación
del
Modelo
Espacialme
1
1ecuación
iecuación
j 1
i 1sej se
v**
E

E
,
al
introducir
(18)
en
sustitución
del empleo homotético
de la v**


ij
ij
'
v**
ecuación ' (6), se tieneEijla E
ecuación del Modelo Shift-Share Espacialment
EijrErij ))(rij  r
1 j 1
i 1 j 1
cialmentei Modificado:
Eij  Eij  Eij  Eij rijEijE(ijriErij)r EEijijv**(r(i rij r) ri )Eij ((Erijij riE) ijv**()(
(1
ij
i
'
v**
v**
ecuación (6), se tiene la ecuación
del
Modelo
Shift-Share
Espacialmente
Modificado:
Eij  Eij  Eij De
Eij r allí
 Eij (se
ri  obtiene
r )  Eij (un
rij  refecto
 Eij )(rij  rineto
) (19
y
i )  ( Eij competitivo
De allív**espacialmente
se obtiene
un
efecto
competitivo
neto y un ef
modificado,
respectivamente.
'
v**
Eij  Eij  Eij  Eij r  espacialmente
Eij (rDe
 Eij se
(rmodificado,
ri )  ( Eij un
Eij efecto
)(rij  ri ) competitivo
(19)
(19) y un efec
i  r )allí
ij 
respectivamente.
obtiene
neto
espacialmente
De allí se obtiene
un efecto modificado,
competitivorespectivamente.
neto y un efecto “locacional”
6) plantea el inconveniente
inconveniente de
de que
S
R
 E
v*
ij
Eno
ENo
(16)
plantea
inconveniente
que
ij 
ij ,

Ede
es decir
decir
la suma
suma
es
la
del el
empleo
espacialmente
modificado
matriz
W,
en lugar
de
una
variacióndedel
empleo homotético.
definición
ij , pesos
S
R
III.
METODOLOGÍA
Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521
espacialmente modificado, respectivamente.
III.
METODOLOGÍA
1. Área de estudio
III.
METODOLOGÍA
III.
METODOLOGÍA
1. Área de estudio
142
Rafael Arias Ramírez y Leonardo Sánchez Hernández
De allí se obtiene un efecto competitivo neto y un efecto “locacional” espacialmente modificado, respectivamente.
III.METODOLOGÍA
1.Área de estudio
La Gran Área Metropolitana (GAM), que constituye el objeto central de este artículo, fue creado como un instrumento legal para regular el desarrollo urbano del sistema de ciudades y centros
de población del Valle Central4. Su configuración está determinada por factores geográficos y su
crecimiento obedece a un patrón de expansión horizontal. Cuenta con una extensión territorial de
196,700 Ha. que equivalen al 3,83% del territorio nacional, e incluye un anillo de contención urbana
de 44,200 ha. (INVU, 2005: 4). Aunque el área de estudio comprende la GAM, el modelo Shift Share
se aplicó a todas las regiones del país como parte del análisis comparativo que se realizó.
.
FIGURA 1
ZONA DE ESTUDIO
Fuente: Arias y Sánchez, 2013.
2.Datos
En la aplicación empírica se ha trabajado con datos sectoriales para el empleo de las siete
regiones de planificación de Costa Rica (formalmente son seis regiones, pero para efectos de este
análisis se dividió la región Central en 2 unidades territoriales: La GAM y el resto de la región Central). Por consiguiente, las regiones consideradas son: La GAM, el resto de la región Central, Chorotega, Brunca, Pacífico Central y las regiones Huetar Norte y Huetar Atlántica, aunque el estudio
se va a centrar en su mayoría en la GAM. La fuente de datos utilizada ha sido la base de datos de
empleo de los Censos de Población y Vivienda del año 2011 y 2000 elaborada por el Instituto Nacional de Estadística y Censos (INEC). La variable a utilizar es la de empleo que el censo define como
4
Decreto del Poder Ejecutivo No 13583-VAH-OFIPLAN del 3 de mayo de 1982, publicado en La Gaceta el 8 de mayo
de ese mismo año.
Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521
143
Análisis de la dinámica regional del empleo utilizando el modelo shift share...
rama de actividad económica. La cual incluye las siguientes 15 categorías: Agricultura; Manufactura, Energía, Construcción, Comercio, Turismo, Transporte. Financiero y seguros, Inmobiliaria,
Administración Pública, Enseñanza, Salud, Otras actividades sociales, Servicio doméstico y Organismos extraterritoriales.
3.
Estimación de la Matriz de pesos espaciales y la auto-correlación espacial
Como se mencionó anteriormente, una matriz de contigüidad se puede construir utilizando
diferentes criterios. Para el cálculo de la I de Moran se utilizó una matriz booleana “W” basada en
criterios de adyacencia. Tal que el valor de wij es uno, cuando dos regiones comparten una frontera
común; y cero, en caso contrario. Los elementos de la diagonal principal son nulos.
En el Cuadro 2 se presenta una matriz binaria para las regiones de planificación de Costa
Rica. Es de esperar que aquellas regiones que comparten frontera común presenten una relación
NIFICACIÓN.más fuerte en comparación con las otras regiones donde no se presenta esta situación.
CUADRO 2
MATRIZ BINARIA PARA LAS REGIONES DE PLANIFICACIÓN.
Huetar
nca Atlántica
Huetar
Norte
0
0
GAM
Resto Región
Central
Chorotega
Pacífico
Central
Brunca
Huetar
Atlántica
Huetar
Norte
0
1
0
1
0
0
0
0
GAM
1
1
1
Resto Región Central
1
1
1
1
1
1
1
0
0
Chorotega 1
0
1
0
1
0
0
1
1
0
Pacífico Central
1
1
1
0
1
0
0
Brunca
0
1
0
1
0
1
0
0
1 Huetar Atlántica
0
0
1
0
0
1
0
1
1
0
Huetar Norte
0
1
1
0
0
1
0
0
1
0
1
Fuente: Arias y Sánchez con información del INEC.
0
La matriz de pesos binaria presenta algunas limitaciones, entre ellas la exclusión de
relaciones asimétricas, que es un requisito incluido en los cinco principios establecidos por Paelink
entre ellas la exclusión
Klaasen, que son además: interdependencia, asimetría, alotopía, no linealidad e inclusión de
n los cinco y principios
ependencia, variables
asimetría,
topológicas. (Mayor & López, 2005, p. 8). Para el análisis del Shift-Share se utilizó una
ayor & López, 2005, p.
variación
de la matriz de pesos Cliff-Ord, donde los elementos de la matriz se calculan como la
a matriz de pesos
Clifflongitud de longitud
la frontera
de la frontera común, ajustada por la distancia inversa entre las localizaciones, o sea,
b jk
w jk 
, donde bjk es la proporción de la frontera común entre j y k con respecto al perímetro
d jk
nes, o sea, total de j, y ,d es la distancia entre las unidades espaciales investigadas5. Por otro lado, con el fin de
jk
n respecto al5perímetro
Se utilizará la distancia en Km vía carreta entre las dos ciudades principales de una región j y una región k.
investigadas 5. Por otro
será estandarizada de
e la relación descrita en
n el criterio de Cliff-Ord,
ación espacial sea más
Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521
144
Rafael Arias Ramírez y Leonardo Sánchez Hernández
facilitar su interpretación, la matriz de pesos será estandarizada de tal forma que los elementos de
cada fila sumen uno. Además de la relación descrita en la matriz binaria, se pueden apreciar otros
aspectos basados en el criterio de Cliff-Ord, puesto que puede observarse con cuál región se espera
la relación espacial sea más fuerte. Esta herramienta permite modificar el esquema propuesto por
Esteban-Marquillas (1972), para incorporar el efecto espacial y utilizar el esquema del Shift-Share
Espacialmente Modificado (MME).
Para determinar la significancia estadística de la I de Moran, se calcula un estadístico z(I)
bajo el supuesto de aleatoriedad en el cálculo del primer y segundo momento de la I de Moran. La
normalidad de este estadístico “depende del número de vínculos considerados y de cómo están
conectados, es decir, de la estructura de la matriz de pesos espaciales” (Mayor y López 2005, 16).
De esta manera, los resultados de la I de Moran para el caso de las regiones de planificación
en conjunto vienen dados por el Cuadro 3. Los resultados a nivel regional sugieren la existencia de
autocorrelación espacial. El estadístico z(I) es significativo a un nivel de significancia del 0,978%.
Esto sugiere que regiones con un elevado empleo se encuentran cerca de otras con un empleo relativamente alto, mientras aquellas con un nivel bajo de empleo, también se encuentran cercanas entre
sí. Además, esta relación se hace más intensa en el 2011, donde la I de Moran es mayor a la correspondiente en 2000.
CUADRO 3
TEST DE AUTOCORRELACIÓN ESPACIAL 2000-2011
Año
I Moran
Z (I)
P
2000
1,1645
59,0876
0,0000
2011
1,2346
57,4876
0,0000
Fuente: Arias y Sánchez con información del INEC.
IV. RESULTADOS: Comportamiento regional del empleo en 2011
1. El sector primario genera el 14% del empleo del país
En términos generales, el censo de 2011 señala que en el sector primario (agricultura y
minas) se emplea el 14% de la población ocupada nacional. Este peso de la producción primaria
representa apenas al 3,8% del empleo en la GAM y llega al 32% y 38,2% en las regiones Brunca
y Atlántica. También es significativo en la región Norte (35,9%). En estas tres, el sector primario
aporta más de una tercera parte del empleo, pero reduce su protagonismo en la Chorotega (18,4%)
y en el resto de la región Central (20,7%). Dentro de las regiones periféricas, la Pacífico Central es
donde este sector tiene un menor peso relativo, con solo un 15,4% del empleo sectorial.
2.
El sector secundario aporta casi una quinta parte del empleo
El sector manufacturero y de la construcción aportan un 17,9% del empleo nacional
según el censo del 2011. Dentro de este sector, la manufactura es la principal actividad con un
12,1% del empleo total, mientras que la construcción genera el 5,8% del empleo restante. Las
actividades de construcción mantienen un peso similar en las diversas regiones, con excepción
de las regiones huetares (Norte y Atlántica), donde la participación cae al 4% del empleo regional. En la GAM, el peso de este sector es de 6% esto hace que el 58% del empleo en actividades
Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521
Análisis de la dinámica regional del empleo utilizando el modelo shift share...
145
de construcción se concentren en esa zona, porcentaje que sube al 70%, cuando se considera
la región Central en su conjunto.
Las actividades manufactureras muestran una clara concentración en la región Central, particularmente en la periferia de la GAM, donde llegan a aportar el 15% del empleo, y en ellas dominan las actividades más tradicionales (alimentos y textiles). No obstante, la industria menos tradicional, de escaso peso en la generación de empleo total, está claramente concentrada en esa región.
En las periféricas, el aporte de las actividades manufactureras no supera al 10% del empleo regional.
Solo en la región Pacífico Central, la manufactura llega al 10,7% del empleo regional, por el peso de
la industria alimentaria vinculada con los productos marinos.
3.
El sector terciario domina el mercado laboral
Las actividades terciarias o de servicios concentran alrededor de uno de cada siete empleos
en el país (68,2%), aunque su composición y peso regional es muy variable. Como era de esperar en
la Gran Área Metropolitana, adquieren el mayor peso aportando tres de cada cuatro empleos de esa
zona, mientras que en la regiones periféricas de amplia base agrícola (región Brunca y Huetares),
los servicios aportan menos del 60% del empleo regional, aunque más de la mitad de sus empleos.
Al interior de las actividades terciarias, los llamados servicios de comercio al por mayor y al
por menor son los mayoritarios con un 18,5% del empleo nacional. Pese a su carácter, no se encuentran bastantes distribuidos regionalmente, mostrando una ligera concentración en la GAM (20,4%).
En todo caso, aportan al menos el 14% del empleo de las regiones con mayor actividad agrícola.
Los servicios estatales y sociales constituyen el segundo bloque en importancia dentro de las
actividades terciarias, con un 23,5% del empleo nacional. Su base fuertemente pública permite una
distribución regional un tanto más equilibrada, aunque la GAM sigue mostrando una sobrerepresentación, pues ahí el sector aporta el 26,7% del empleo, en tanto que en la región Norte solo genera
el 15% del empleo regional.
Dentro de ellos, los servicios de administración del Estado son los que generan más empleo
(11,9% del empleo nacional), seguidos de la educación (7,1%) y los servicios de salud (4,5%), aunque
estos últimos muestran una mayor concentración en la región Central y en la GAM.
Los servicios de turismo y transporte ocupan el tercer lugar con un 12,2% del empleo del
país. Las actividades turísticas, principalmente servicios de hotelería y de comidas, adquieren su
mayor protagonismo en la región Pacífico Central y Chorotega, donde generan más del 11% del
empleo local. El transporte tiene a ser más importante dentro de la GAM (8,4%) y la región Huetar
Atlántica (6,8%).
Los servicios productivos (intermediación financiera y servicios profesionales) generan solo
un 3,3% del empleo nacional y tienen la mayor concentración en la GAM, donde llegan a generar
3,4% del empleo local. Esto hace que cerca del 77% del empleo de estos sectores se concentre en
la GAM, dominio que absorbe el 56% del empleo nacional. Por último, los servicios básicos como
el suministro de energía eléctrica y agua, aportan el 2,1% restante del empleo nacional y tienden a
mostrar una distribución regional más homogénea.
Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521
Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521
1.047
Organismos extraterritoriales
100%
0,1%
4,6%
4,7%
5,1%
7,1%
14,4%
0,7%
3,8%
8,4%
4,6%
20,4%
6,0%
1,9%
14,4%
3,8%
179.819
54
8.756
5.344
7.554
13.675
17.514
525
3.111
9.699
6.045
30.768
11.684
4.783
23.158
37.149
100%
0,0%
4,9%
3,0%
4,2%
7,6%
9,7%
0,3%
1,7%
5,4%
3,4%
17,1%
6,5%
2,7%
12,9%
20,7%
Resto Región
Central
Fuente: Arias y Sánchez con información del INEC.
943.517
43.172
Servicio domestico
Total
44.007
Otras actividades sociales
6.488
Inmobiliaria
48.173
35.854
Financiero y seguros
Salud
79.328
Transporte
67.402
42.992
Turismo
Enseñanza
192.150
Comercio
136.206
56.729
Construcción
Administracion Publica
17.502
136.335
Manufactura
Energia
36.132
GAM
Agricultura
Región
109.693
11
5.260
3.783
4.294
8.910
11.581
1.157
1.519
4.977
12.124
17.657
6.991
3.798
7.435
20.196
100%
0,0%
4,8%
3,4%
3,9%
8,1%
10,6%
1,1%
1,4%
4,5%
11,1%
16,1%
6,4%
3,5%
6,8%
18,4%
Chorotega
86.544
1
3.563
3.660
3.583
5.756
8.812
804
959
5.121
9.764
14.705
5.116
2.060
9.297
13.343
100%
0,0%
4,1%
4,2%
4,1%
6,7%
10,2%
0,9%
1,1%
5,9%
11,3%
17,0%
5,9%
2,4%
10,7%
15,4%
Pacífico Central
108.712
8
5.058
3.672
4.536
8.486
8.061
424
1.447
4.886
5.152
17.058
6.081
1.843
7.235
34.765
Brunca
100%
0,0%
4,7%
3,4%
4,2%
7,8%
7,4%
0,4%
1,3%
4,5%
4,7%
15,7%
5,6%
1,7%
6,7%
32,0%
130.813
1
3.880
3.278
3.937
8.316
9.678
180
1.055
8.895
5.368
18.802
5.550
2.530
9.340
50.003
100%
0,0%
3,0%
2,5%
3,0%
6,4%
7,4%
0,1%
0,8%
6,8%
4,1%
14,4%
4,2%
1,9%
7,1%
38,2%
Huetar Atlántica
CUADRO 4
COMPOSICIÓN DEL EMPLEO SEGÚN RAMA DE ACTIVIDAD ECONÓMICA Y REGIÓN, 2011
115.177
6
4.864
3.100
3.019
7.069
7.133
218
1.219
4.386
5.888
19.204
5.320
3.111
9.333
41.307
100%
0,0%
4,2%
2,7%
2,6%
6,1%
6,2%
0,2%
1,1%
3,8%
5,1%
16,7%
4,6%
2,7%
8,1%
35,9%
Huetar Norte
1.674.275
1.128
74.553
66.844
75.096
119.614
198.985
9.796
45.164
117.292
87.333
310.344
97.471
35.627
202.133
232.895
Total
100%
0,1%
4,5%
4,0%
4,5%
7,1%
11,9%
0,6%
2,7%
7,0%
5,2%
18,5%
5,8%
2,1%
12,1%
13,9%
146
Rafael Arias Ramírez y Leonardo Sánchez Hernández
Análisis de la dinámica regional del empleo utilizando el modelo shift share...
4.
147
Resultados específicos del mercado laboral en la GAM: 2000 - 2011
Globalmente, la población ocupada de GAM pasa de 762.311 personas en 2000, a 943.517,
once años más tarde, para un crecimiento anual del 1,96%. Esto significa que cerca de 16.500 personas encontraron, en promedio, empleo cada año.
Por actividad económica, el sector primario experimenta una contracción absoluta en este
periodo. Esto hace que su aporte al empleo total pase del 6% en 2000, a tan solo cerca del 3,8% en
el 2011. Probablemente esta pérdida de empleos se encuentre asociada a la producción agropecuaria
de baja calificación técnica (que representa el mayor porcentaje), mientras que los servicios agrícolas se transforman en el subsector más dinámico de todos.
La industria manufacturera de la GAM, durante este periodo, muestra un dinamismo muy
por debajo de la media nacional al decrecer a un ritmo del 14,1% en el periodo analizado, mientras
que la tasa a nivel nacional fue de -7,6%. Esto provocó que se perdieran en promedio cerca de 2.040
empleos cada año entre el 2000 y el 2011, disminuyendo alrededor de 6 puntos porcentuales en su
participación relativa, al pasar del 20,8% en 2000 al 14,4% en el 2011.
Las actividades de construcción completan las actividades secundarias y estas muestran un
comportamiento muy por debajo del promedio del país, creciendo a una tasa en todo el periodo del
6,6% (menos de 3 veces la media nacional (19,5%)) y siendo la región de planificación de menor
crecimiento del periodo en este sector. A pesar de lo anterior este crecimiento positivo le permite
incorporar al mercado laboral cerca de 320 trabajadores de la construcción en promedio cada año,
aunque la participación de este sector decae del 7% al 6%.
Los servicios básicos de origen estatal, agua y electricidad, pese a mantener su marginal
aporte al empleo, muestran un fuerte crecimiento en conjunto dentro de la GAM, pero debido básicamente al sector eléctrico donde han existido fuertes inversiones en los últimos años. La tasa de
crecimiento del empleo en este sector supera el 50% en todo el periodo, aunque está muy por debajo
de la media nacional que lo hizo en 85,6% y del resto de regiones del país.
Por el contrario, el sector de transporte y comunicaciones dentro de la GAM, se expandió
a una tasa de crecimiento durante el periodo de 59,4% muy similar a la media nacional (59,6%) y
superior a los valores de las regiones Pacífico Central (33,6%) y Huetar Atlántica (40,2%).
Las actividades turísticas (restaurantes y hoteles) muestran un dinamismo moderado al
expandirse a un ritmo del 22% entre 2000 y 2011, generando un 4,3% de los nuevos empleos creados en la GAM y mantiene la misma participación en el empleo total del 4,6%. En comparación con
la media nacional, el crecimiento de la GAM es bajo, el país en conjunto creció en esta actividad al
38,1% y con excepción de la región Huetar Atlántica (23,6%), el resto de regiones más que duplicaron el crecimiento de la GAM.
Con respecto al comercio, entre el 2000 y el 2011, la cantidad de personas empleadas en este
sector aumenta en 66.022 trabajadores dentro de la GAM, esto le permitió crecer al 29,2% para todo
el periodo, aunque dicha tasa de crecimiento es menor a la media nacional (44,4%) y al resto de
regiones (todas más que duplican el crecimiento de la GAM).
El sector financiero y de seguros, creció dentro de la GAM en un 55% entre el 2000 y el 2011, a
pesar de ello su participación en el empleo total, creció menos de 1%, lo cual explica que solo aporte el 7%
de los nuevos empleos creados en la GAM. Este crecimiento es muy similar al del país (55,9%).
El sector inmobiliario, presentó una caída importante de empleo en la GAM, al decrecer a
una tasa del 87,6%, es decir se perdieron entre el 2000 y el 2011 cerca de 45.827 empleos, disminuyendo su participación del 6,9% en 2000 al 0,7% en 2011.
La administración pública fue la que presentó por mucho el mayor crecimiento dentro de la
GAM. Entre todas las actividades, entre el 2000 y el 2011 creció en un 230%, esto implicó un crecimiento absoluto para el periodo de alrededor de 94.938 trabajadores, aumentando su participación
relativa en el empleo del 5,4% al 14,4% entre el 2000 y el 2011. Aunque todas las regiones restantes
Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521
148
Rafael Arias Ramírez y Leonardo Sánchez Hernández
presentaron más de un 100% de crecimiento, ninguna supera el crecimiento experimentado en la
GAM que aglutinó el 53% del crecimiento absoluto de este sector a nivel nacional.
El empleo en el sector enseñanza también mostró un crecimiento en la GAM cercano al
43% entre el 2000 y el 2011, esto implicó un incremento absoluto de alrededor de 26.780 personas,
aumentando su participación del 6,2% al 7,1% entre el 2000 y el 2011. A pesar de lo anterior, el crecimiento de la GAM es menor a la media nacional que fue del 56,6% y al resto de regiones donde el
crecimiento fue superior al 60%.
Por último, el sector salud creció dentro de la GAM en un 59,6% entre el 2000 y el 2011, dicho
aumento significó cerca de 18.000 nuevos empleos en este sector, aumentando la participación del
4% en 2000 al 5,1% en 2011 y explicando alrededor del 10% de todo el crecimiento del empleo en la
GAM y el 62% del nuevo empleo generado en salud en todo el país para el periodo analizado.
CUADRO 5
CRECIMIENTO ABSOLUTO DEL EMPLEO POR ACTIVIDAD ECONÓMICA Y REGIÓN
ENTRE EL 2000 Y EL 2011
Actividad económica
GAM
Resto
Región
Central
Chorotega
Pacífico
Central
Brunca
Huetar
Atlántica
Huetar
Norte
Total
Agricultura
-3.977
-4.104
-1.771
-1.214
-3.621
-4.187
-3.220
-22.094
Manufactura
-11.992
-1.653
-548
-753
-476
-592
-501
-16.515
Energia
9.728
2.074
1.778
617
622
663
951
16.433
Construcción
10.370
1.593
972
820
711
827
606
15.898
Comercio
66.022
7.997
4.187
3.666
4.825
5.002
3.723
95.422
Turismo
13.429
1.579
2.380
2.632
1.280
1.655
1.145
24.099
Transporte
29.689
3.214
1.610
2.286
1.736
3.785
1.503
43.822
Financiero y seguros
12.925
1.094
480
349
507
396
443
16.193
Inmobiliaria
-44.257
-2.830
-1.478
-1.093
-1.267
-1.909
-968
-53.802
Administracion Publica
84.611
15.018
8.511
6.128
6.454
7.486
5.542
133.750
Enseñanza
26.780
4.360
2.945
1.780
2.537
2.861
1.946
43.208
Salud
19.096
2.476
1.524
1.478
1.867
1.547
1.109
29.097
Otras actividades sociales
18.381
1.767
1.297
1.186
1.161
2.215
988
26.996
Servicio domestico
14.768
2.213
1.286
750
859
754
1.010
21.638
Organismos
extraterritoriales
-1.039
-313
-19
-6
-11
-8
-21
-1.416
Fuente: Arias y Sánchez con información del INEC
Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521
149
Análisis de la dinámica regional del empleo utilizando el modelo shift share...
CUADRO 6
TASA DE CRECIMIENTO ABSOLUTA DEL EMPLEO POR ACTIVIDAD ECONÓMICA Y REGIÓN
ENTRE EL 2000 Y EL 2011
GAM
Resto
Región
Central
Chorotega
Pacífico
Central
Brunca
Huetar
Atlántica
Huetar
Norte
Total
Agricultura
-21,3%
-21,6%
-1,2%
-4,8%
-16,8%
3,5%
11,2%
-8,7%
Manufactura
-14,1%
5,8%
2,5%
-6,7%
14,7%
19,1%
40,7%
-7,6%
Energia
54,0%
97,5%
82,9%
185,7%
153,5%
226,9%
180,0%
85,6%
Construcción
6,6%
42,9%
40,2%
21,6%
66,7%
30,9%
71,2%
19,5%
Comercio
29,2%
70,8%
87,2%
78,1%
57,0%
66,9%
129,0%
44,4%
Turismo
22,0%
45,9%
94,1%
41,4%
53,4%
23,6%
95,9%
38,1%
Transporte
59,4%
80,0%
84,4%
33,6%
67,9%
40,2%
74,0%
59,6%
Financiero y seguros
55,1%
59,0%
77,0%
53,4%
59,5%
49,0%
53,9%
55,9%
Inmobiliaria
-87,6%
-84,3%
-33,8%
-37,8%
-71,7%
-92,0%
-80,9%
-84,6%
Administracion Publica
230,1%
139,1%
179,0%
194,8%
156,1%
165,1%
163,9%
205,0%
Enseñanza
42,3%
77,4%
71,1%
82,9%
89,2%
64,4%
105,4%
56,6%
Salud
59,6%
93,0%
78,2%
53,3%
53,7%
61,0%
72,2%
63,3%
Otras actividades sociales
62,2%
104,9%
97,5%
109,0%
114,2%
0,2%
112,5%
67,7%
Servicio domestico
19,5%
61,8%
67,2%
94,4%
140,9%
110,5%
97,0%
40,9%
Organismos
extraterritoriales
-43,9%
-90,4%
-67,6%
-90,0%
-60,0%
-93,3%
-83,8%
-55,7%
Actividad económica
Fuente: Arias y Sánchez con información del INEC
5.
Dinámica específica del empleo en la GAM 2000-2011, análisis de efecto nacional, sectorial y
competitivo neto espacial
La dinámica de la evolución del empleo en la GAM al igual que el resto de regiones del país, se
encuentra influenciada por aspectos propios de la dinámica global de empleo en el país, la composición productiva de la región y la dinámica particular que tienen las distintas ramas en la región. De
esta manera, el método Shift-Share Espacialmente Modificado, permite descomponer el crecimiento
del empleo de la región en cuatro componentes. El primero alude al efecto crecimiento nacional
y dice cuánto sería el crecimiento del empleo si en la región se hubiera expandido al ritmo medio
nacional. El segundo componente sería el aportado por el efecto sectorial de la región, el cual ofrece
evidencia del crecimiento del empleo, porque la región cuenta con las ramas más dinámicas a nivel
nacional. El tercer y cuarto efecto (regional o competitivo y “locacional”) sería el de la dinámica
regional propiamente dicha y muestra el aumento del empleo por efecto de un mayor dinamismo de
las ramas en la región que sus contrapartes a nivel nacional. Donde los dos primeros efectos permanecen invariantes con respecto al esquema clásico.
Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521
150
Rafael Arias Ramírez y Leonardo Sánchez Hernández
El Cuadro 7 presenta esta descomposición para la GAM. El empleo en esta región se expandió
a un ritmo medio anual del 1,96% (181 mil personas entre 2000 y 2011) por debajo de la media nacional (2,32%). Esto hace que el efecto crecimiento nacional explique más del 100% del crecimiento
total del empleo regional (109%). Su origen se encuentra en la producción industrial o manufactura
(25,1%), que es importante en esta región, en el comercio (23,5%) y, en menor medida, en actividades
como el sector inmobiliario (8,3%), transporte (7,9%), agricultura (7,3%) y enseñanza (7,5%).
Cuando el efecto nacional representa un porcentaje mayor al 100% del cambio en el empleo,
se afirma que el crecimiento del empleo hubiera sido mayor si la región creciera al mismo ritmo que
el país como un todo. En este sentido, el efecto nacional nos muestra que si la GAM hubiese crecido
al ritmo medio del empleo nacional, la zona hubiera tenido cerca de 37.100 empleos más en 2011.
Esta pérdida de empleos que experimenta la GAM por no haber crecido al menos como el promedio
nacional se da en todos los sectores analizados con excepción de la administración pública. A continuación se muestra el comportamiento por sector:
- El agrícola hubiera tenido una pérdida menor de empleos entre el 2000 y el 2011, de alrededor de
3.977 en comparación con la experimentada en la realidad que fue de 9.768 empleos.
- La industria hubiera decrecido en la mitad de los que realmente sucedió, es decir, en lugar de
perder 22.400 empleos hubiera perdido cerca de 11.991 para el periodo analizado. En el caso del
sector transporte, financiero y seguros el crecimiento de la GAM y del país es muy similar, y la
pérdida de empleos no representa más de 300 trabajadores.
- El sector construcción hubiese crecido en cerca de 6.900 empleos más de lo que creció y el sector
energía en alrededor de 3.600; pero entre todas las actividades, es el sector comercio el que más
empleos pierde por no crecer igual al promedio nacional, en total pierde cerca de 22.576 empleos.
- Las actividades turísticas (alojamiento, hospedaje y restaurantes) dejan de crecer en cerca de
5.673 empleos, la enseñanza en 6.733 y las actividades inmobiliarias en alrededor de 1.570. De
igual forma la salud presenta un decrecimiento de alrededor de 1.111 empleos; y los servicios
domésticos, de 7.710.
- Como se mencionó anteriormente, el sector de la administración pública fue el único que
creció por encima del promedio nacional, y en este caso, si la GAM hubiera crecido como lo
hizo el país en esta actividad hubiese experimentado una pérdida de empleos cercana a los
10.327 empleos.
El efecto sectorial, también tiene un impacto positivo que explica el 14,5% del cambio en el
empleo de la región durante este periodo, lo que es equivalente a ganar cerca de 26.225 empleos.
Lo anterior indica que existe concentración de empleo en la mayoría de ramas que a nivel nacional tiene un alto dinamismo, y que a pesar de la pérdida en actividades como la agrícola (-9,4%),
la actividad industrial (-31,7%) y la construcción (-2,7%) el efecto negativo es compensado por el
dinamismo positivo de otras ramas como la administración pública (40,2%), el comercio (12,9%), el
transporte (8,5%) y la salud (5,8%) entre otras, que son las ramas que tienen mayor influencia en el
efecto sectorial en esta región.
Por otra parte, la GAM se caracteriza por una disminución en la dinámica regional (efecto
regional o competitivo negativo (-38%)). Con excepción de la administración pública y organismos extraterritoriales, el resto de actividades generadoras de empleo en la región crecieron por
debajo de la media de las regiones vecinas; lo que implica un aprovechamiento inferior al que
derivaría de una buena evolución de las regiones vecinas. Las ramas que tuvieron una mayor
influencia positiva en el efecto regional son solo dos, la administración pública (5,3%) y organismos extraterritoriales; (0,1%) no obstante la magnitud de este efecto se ve contrarrestada por la
pérdida de dinamismo en la rama agrícola (-10,4%), la industria (-1,1%), sector energía (-4,6%), así
como el de construcción (-3,4%), el comercio (-10,5%), turismo (-3,3%), la enseñanza (3,5%) entre
Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521
151
Análisis de la dinámica regional del empleo utilizando el modelo shift share...
otros explicados en la Cuadro 7. A pesar de ello, la dinámica regional llega a explicar el 38% del
cambio en el empleo total en el periodo para la GAM, lo que es equivalente a decir que explica la
pérdida de alrededor de 68.940 empleos en la región.
CUADRO 7
RESULTADOS DEL ANÁLISIS SHIFT SHARE ESPACIALMENTE MODIFICADO PARA LA GAM, 2000-2011
Rama de Actividad
Cambio
Total
Efecto
Nacional
Efecto
Sectorial
Efecto
Competitivo
Neto Espacial
Efecto
“Locacional”
Espacial
Cambio total absoluto
181.206
218.306,09
26.225,95
-68.940,20
5.614,16
Cambio total relativo
100,0%
120,5%
14,5%
-38,0%
3,1%
Agricultura
-5,4%
7,3%
-9,4%
-10,4%
7,2%
Manufactura
-12,4%
25,1%
-31,7%
-4,6%
-1,1%
Energia
3,4%
1,8%
3,6%
-2,0%
0,0%
Construcción
1,9%
8,4%
-2,7%
-3,4%
-0,4%
Comercio
24,0%
23,5%
12,9%
-10,5%
-1,9%
Turismo
4,3%
5,6%
1,8%
-3,3%
0,2%
Transporte
16,3%
7,9%
8,5%
-0,1%
0,0%
Financiero y seguros
7,0%
3,7%
3,5%
-0,1%
0,0%
Inmobiliaria
-25,3%
8,3%
-32,7%
-0,6%
-0,2%
Administracion Publica
52,4%
6,5%
40,2%
5,3%
0,4%
Enseñanza
11,1%
7,5%
7,3%
-3,5%
-0,2%
Salud
9,9%
4,8%
5,8%
-0,5%
-0,1%
Otras actividades sociales
9,3%
4,3%
5,9%
-0,7%
-0,1%
Servicio domestico
3,9%
5,7%
2,4%
-3,7%
-0,6%
Organismos
extraterritoriales
-0,5%
0,3%
-0,9%
0,1%
0,0%
Fuente: Arias y Sánchez con información del INEC
6.
GAM: Descomposición del Efecto Locacional
El efecto “locacional” mide el grado de especialización en una determinada rama de
actividad, lo que permite identificar si la región se especializa en aquellas ramas en las que
ganó ventaja con respecto a las regiones vecinas. A diferencia de los otros efectos, este tiene
cuatro posibles interpretaciones: a) desventaja competitiva con especialización, b) desventaja
competitiva sin especialización, c) ventaja competitiva sin especialización y d) ventaja competitiva con especialización (ver Cuadro 8).
Del Cuadro 8 se deduce que la GAM presenta un efecto locacional positivo que llega a explicar
un 3,1% del cambio en el empleo presentado entre 2000 y el 2011. Es decir, la región presentó un
aprovechamiento superior al que deriva de especializarse en aquellas actividades dinámicas donde
ganó ventaja respecto a otras regiones (agricultura, turismo, administración pública y organismos
Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521
152
Rafael Arias Ramírez y Leonardo Sánchez Hernández
extraterritoriales). A pesar de la falta de especialización que presentó la región en el resto de actividades, el efecto positivo en las cuatro ramas mencionadas anteriormente hizo que la GAM ganara
cerca de 5.614 empleos que, como se mencionó anteriormente, explican el 3,1% del crecimiento de
la GAM entre el 2000 y el 2011.
El Cuadro 8 resume los resultados del efecto “locacional” para la GAM según actividad económica. Como es de esperar, el sector agrícola es la única actividad dentro de la región que presenta
un patrón negativo de desventaja competitiva con especialización. Es decir, la región ha estado especializándose en una actividad en la cual ha perdido ventaja competitiva respecto a otras regiones
vecinas; esta desventaja explica por qué la región tuvo una contracción tan fuerte en el número de
trabajadores agrícolas y por qué otras regiones absorbieron ese empleo. Precisamente ese comportamiento equivocado de especialización provocó que la región expulsara cerca de 2.700 empleos agrícolas durante este periodo (1990-2009).
CUADRO 8
GAM: RESULTADOS DEL EFECTO LOCACIONAL SEGÚN RAMA DE ACTIVIDAD ECONÓMICA
Efecto
“Locacional”
(EL)
Especialización
(Eij - E�ij)
Competitividad
(rij - ri* )
Resultado
Agricultura
+
-
-
Desventaja Competitiva, Sin Especialización
Manufactura
-
+
-
Desventaja Competitiva, Especialización
Energia
-
+
-
Desventaja Competitiva, Especialización
Construcción
-
+
-
Desventaja Competitiva, Especialización
Comercio
-
+
-
Desventaja Competitiva, Especialización
Turismo
+
-
-
Desventaja Competitiva, Sin Especialización
Transporte
-
+
-
Desventaja Competitiva, Especialización
Financiero y seguros
-
+
-
Desventaja Competitiva, Especialización
Inmobiliaria
-
+
-
Desventaja Competitiva, Especialización
Administracion
Publica
+
+
+
Ventaja Competitiva, Especialización
Enseñanza
-
+
-
Desventaja Competitiva, Especialización
Salud
-
+
-
Desventaja Competitiva, Especialización
Otras actividades
sociales
-
+
-
Desventaja Competitiva, Especialización
Servicio domestico
-
+
-
Desventaja Competitiva, Especialización
Organismos
extraterritoriales
+
+
+
Ventaja Competitiva, Especialización
Rama de Actividad
Fuente: Arias y Sánchez con información del INEC
Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521
Análisis de la dinámica regional del empleo utilizando el modelo shift share...
153
7.Análisis regional comparativo
De acuerdo con las propiedades del análisis Shift-Share que destaca Kiel (1992, p. 471), si se
suman todos los efectos en i, es decir, todas las ramas de actividad, los efectos obtenidos son atribuibles a la región. En el Cuadro 9 se presentan los resultados obtenidos para el método Shift Share, a
un nivel regional, dejando de lado la especificidad sectorial.
La GAM presenta un efecto nacional mayor en términos de empleos ganados que todas las
demás regiones. En comparación con el resto de regiones, este valor es cerca de ocho veces más
(exceptuando el resto de la región central que es de 5,5 veces), lo cual no es de extrañar ya que esta
zona es muy dominante dentro del país; sin embargo, como se explicó anteriormente, la importancia en relación al cambio en el empleo de la región puede variar. Esta situación se explica en parte
por la diferencia en la estructura de empleo (Eij) que hay en esta región con respecto a las demás;
ya que en 2000 el 58,5% del empleo estaba concentrado en esta región, mientras que en el año 2011
este porcentaje disminuye a un 56,3%.
No obstante, parte de la concentración de empleos en la GAM se debe a la concentración de
ramas de rápido crecimiento, principalmente del sector público. Lo anterior se refleja en el Cuadro
9, donde se muestra que la GAM, junto con la región Chorotega y Pacífico Central, son las únicas
que presentan un efecto sectorial positivo.
El signo negativo del efecto sectorial, tal como se puede observar en las regiones Brunca,
Huetar Atlántica y Huetar Norte, así como el resto de la región Central, indica una débil concentración en industrias de rápido crecimiento, o bien, una alta concentración en industrias de poco
crecimiento como la agricultura, ganadería, silvicultura y pesca; explotación de minas y canteras
e industria. Así regiones que tienen una alta dependencia de la agricultura, ganadería, silvicultura
y pesca, están asociadas a un efecto sectorial negativo mayor como es el caso de la Región Brunca.
A nivel regional, el método indica que solo la GAM perdió dinámica o ventaja competitiva con
respecto a las regiones vecinas. No obstante, la magnitud del efecto sectorial o concentración en
industrias de rápido crecimiento le permite a la GAM contrarrestar la pérdida de competitividad en
término de empleos perdidos.
Un signo positivo en el efecto “locacional” indica que la región se especializa en ramas en las
cuales ganó ventaja competitiva sobre las regiones vecinas. El método espacialmente modificado
sugiere que de las siete regiones en Costa Rica analizadas, solo la GAM presentó un efecto “locacional” positivo.
Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521
Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521
100,0%
181.206,0
39.598,0
37.099,0
24.663,0
22.274,0
28.435,0
39.454,0
Gran Área Metropolitana
Resto Región Central
Región Chorotega
Región Pacífico Central
Región Brunca
Región Huetar Atlántica
Región Huetar Norte
Fuente: Arias y Sánchez con información del INEC.
100,0%
Absoluto
100,0%
100,0%
100,0%
100,0%
100,0%
%
Cambio en el Empleo
(Enj+Esj+Erj)
Regiones de Planificación
21.685,1
29.318,4
24.753,6
17.721,1
20.789,0
40.155,7
218.306,1
Absoluto
55,0%
103,1%
111,1%
71,9%
56,0%
101,4%
120,5%
%
Efecto Nacional ENj
-7.428,2
-8.825,8
-7.570,9
906,4
2.364,6
-5.672,1
26.226,0
Absoluto
-18,8%
-31,0%
-34,0%
3,7%
6,4%
-14,3%
14,5%
%
Efecto Sectorial ESj
29.579,3
10.362,4
12.704,4
8.081,6
14.957,2
11.536,7
-68.940,2
Absoluto
75,0%
36,4%
57,0%
32,8%
40,3%
29,1%
-38,0%
%
Efecto Competitivo Neto
Espacial ECNEj
Componentes del cambio en el empleo
-4.382,2
-2.420,0
-7.613,1
-2.046,1
-1.011,8
-6.422,3
5.614,2
Absoluto
-11,1%
-8,5%
-34,2%
-8,3%
-2,7%
-16,2%
3,1%
%
Efecto “Locacional“
Espacial ELEj
CUADRO 9
COSTA RICA: RESULTADOS DEL ANÁLISIS SHIFT SHARE ESPACIALMENTE MODIFICADO POR REGIÓN, 2000-2011
154
Rafael Arias Ramírez y Leonardo Sánchez Hernández
Análisis de la dinámica regional del empleo utilizando el modelo shift share...
155
V.CONCLUSIONES
- Los resultados muestran que la estructura productiva de la GAM y el país en general presentan
una fuerte y creciente tercerización del mercado laboral pese a que todavía la producción agrícola es una de las más importantes fuentes de empleo en las regiones Huetar Norte, Huetar Atlántica y Brunca. De igual forma se muestran grandes disparidades regionales en la concentración y
tipo de empleo en el país.
- Dentro de la GAM, la expansión de los servicios tuvo el principal aporte al crecimiento del
empleo. Destaca el crecimiento en los empleos de la administración pública que explica cerca
del 53% del crecimiento del empleo total en la región entre el 2000 y el 2011. Así mismo, toman
importancia el comercio, el sector transporte, y en menor medida la enseñanza y la salud, que
también presentan un fuerte componente estatal. Las actividades financieras de igual manera
mostraron un crecimiento significativo.
- El sector agropecuario, la manufactura y en especial el sector inmobiliario, fueron los que mostraron una contracción en el empleo entre el 2000 y el 2011 dentro de la GAM, aunque esta tendencia se presentó también a nivel nacional. Las excepciones fueron las regiones Huetar Norte y
Atlántica que ganan empleo en agricultura, aunque dicho crecimiento no fue lo suficientemente
significativo para compensar el valor a nivel nacional.
- En términos de tasas de crecimiento de las actividades económicas generadoras de empleo entre
el 2000 y el 2011, resalta un hecho importante: con excepción de la administración pública, el
resto de actividades presentó un crecimiento por debajo de la media nacional y de la experimentada por el resto de regiones del país. Esto implica que si la GAM hubiese crecido al ritmo nacional, la cantidad de nuevos empleos que hubiera generado en el periodo analizado sería mayor en
cerca de 37 mil puestos de trabajo.
- Los resultados del Shift Share espacialmente modificado son interesantes, pues muestran que la
GAM se especializa en actividades productivas en las cuales presenta ventajas competitivas, pero
a su vez lo hace en actividades donde no las tiene. Esto demuestra en términos económicos un
problema de asignación de recursos, pues existe una alternativa de especialización productiva
que podría mejorar el bienestar y que no está siendo suficientemente aprovechada. En este sentido, se puede generar una disyuntiva entre la posibilidad de que las autoridades públicas intervengan con medidas de fomento para canalizar recursos hacia las actividades ventajosas, o dejar que
sea el mercado el que se encargue de hacer dicha asignación. Ambas medidas tienen un costo,
que no se puede cuantificar en este estudio, pero que las instituciones públicas pertinentes
deben evaluar.
- Los resultados sobre los principales generadores de empleo en la GAM, sin duda ofrecen elementos para el diseño de políticas de desarrollo regional y un análisis más desagregado por actividades económicas y por subregiones, ciudades intermedias u otra unidad de análisis que los Censos
de Población y Vivienda permitan realizar.
VI.Bibliografía
Andrikoplous, Andreas, James A. Brox y Emanuel Carvalho, 1990, “Shift-share analysis and
potential for Predicting Regional Growth Patterns: Some Evidence for the region of Quebec,
Canada”, Grownth and change, vol. 21, núm. 1, Kentucky, Wiley-Blackwell, pp. 1-10.
Bartles, Cornelis, William Nicol y Jacob van Duijn, 1982, “Estimating the Impact of Regional Policy:
A Review of Applied Research Methods”, Regional Science and Urban Economics, vol. 12,
núm. 1, Amsterdam, Elsevier, pp. 3-41.
Dinc, M.; Haynes, K.e.; Qiangsheng, l. (1997): “A comparative evaluation of shiftshare models and
their extensions”, Australasian Journal of Regional Studies, vol.4, nº 2, p. 275-302.
Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521
156
Rafael Arias Ramírez y Leonardo Sánchez Hernández
Dunn, Edgar. (1960). A statistical and analytical technique for regional analysis Papers of the
Regional Science Association, 6, 97-112.
Dunn, Edgar. (1967). The Location of Agricultural Production. Gainesville: University of Florida
Press.
Esteban-Marquillas, Joan Maria. (1972). Shift and Share analysis revisited. Regional and Urban
Economics, 2 (3), 249-261.
Gerking, Shelby y Joseph Barrington, 1981, “Are Regional Effects Constant Over Time?”, Journal of
Regional Science, vol. 21, núm. 2, Nueva York, Wiley-Blackwell, pp. 163-174.
Haynes, K.e.; Machunda, Z. B. (1987): “Considerations in extending Shift-Share analysis: Note”,
Growth and Change, nº 18, spring, p. 69-78.
Herzog, Henry & Olsen, Richard. (1977). Shift-Share Analysis Revisited: The Allocation Effect and
the Stability of Regional Structure. Journal of Regional Science, 17 (3), 441-454.
Keil, Stanley. (1992). On the value of homotheticity in the Shift-Share framework. Growth and
Change, 23 (3), 469-493.
Ledebur, Larry y Ronald Moomaw, 1983, “A Shift-Share Analysis of Regional Labor Productivity in
Manufacturing”, Growth and Change, vol. 14, núm. 1, Kentucky, Wiley-Blackwell, pp. 2-9.
Mayor, Matías & López, Ana Jesús. (2005). El análisis Shift-Share espacial: nuevos desarrollos.
Universidad de Oviedo, Departamento de Economía Aplicada.
Mayor, Matías & López, Ana Jesús. (2006). Shift-Share espacial versus filtrado espacial. Una
aplicación al empleo regional. Universidad de Oviedo, Departamento de Economía Aplicada.
Mayor, Matías; López, Ana Jesús & Pérez, Rigoberto. (2004). La elaboración de escenarios basados
en análisis shift-share. Aplicación a las perspectivas de empleo regional. XVIII Reunión
ASEPELT-España, Actas “Anales de Economía Aplicada”. León, España.
Mead, Arthur y Glenworth Ramsay, 1982, “Analyzing Differential Responses of a Region to Business
Cycles”, Growth and Change, vol. 13, núm. 1, Kentucky, Wiley-Blackwell, pp. 38-42.
Nazara, Suahasil & Hewings, Geoffrey. (2004). Spatial structure and Taxonomy of Decomposition in
Shift-Share analysis. Growth and Change, 35 (4), 476-490.
Nijkamp, P. et al. (1986): Handbook of regional and urban economics. Amsterdam : North-Holland.
(FEG/1001 01 HAN 1)
Senf, David, 1988, “Shift-Share Analysis of Rural Retail Trade Patterns”, Regional Science
Perspectives, vol. 18, núm. 2, Minnesota, Mid-Continent Regional Science Association, pp.
29-43.
Stevens, B.H.; Moore, c. (1980): “A critical review of the literature on Shift-Share as a forecasting
technique”, Journal of Regional Science, vol. 20, nº 4.
Toral, María Amparo. (2001). El factor espacial en la convergencia de las regiones de la Unión
Europea: 1980-1996. Tesis doctoral. Universidad Pontificia Comillas, Madrid, España.
Todos los derechos reservados. Universidad de Costa Rica. Este artículo se encuentra licenciado con Creative Commons
Reconocimiento-NoComercial-SinObraDerivada 3.0 Costa Rica. Para mayor información escribir a revista.iice@ucr.ac.cr
Ciencias Económicas 31-No. 2: 2013 / 135-156 / ISSN: 0252-9521