Matemática 1 - CPA U2 - Función constante
Anuncio

Matemática 1 - CPA
Unidad 3: Función Lineal
Contenidos
U2 - Función constante, Función lineal
Función constante.
Es la función real definida por:
f (x) = c,
con c ∈ R, constante
Propiedades
a) Dom(f ) = R,
Rec(f ) = {c}
b) Su gráfica es la recta paralela (o igual) al eje X: y = c.
c) No es inyectiva.
Función lineal.
Es la función real de la forma:
f (x) = ax + b,
con a, b ∈ R,
a 6= 0
Propiedades
a) Dom(f ) = R,
Rec(f ) = R
b) Gráfica de f (x) = ax + b.
Para graficar f (x) = ax + b se sustituye f (x) por la variable y, y se grafica la ecuación y = ax + b.
• Luego: La gráfica de f (x) = ax + b es una recta.
• Esta recta intercepta (o corta) al eje X en el punto (− ab , 0), y al eje Y en el punto (0, b).
• La gráfica de f (x) = ax + b es una recta oblicua, con pendiente a.
Ejemplo.
Cuando a > 0, la gráfica de f es creciente.
Cuando a < 0, la gráfica de f es decreciente.
Si x1 ≤ x2 entonces f (x1 ) ≤ f (x2 )
Si x1 ≤ x2 entonces f (x1 ) ≥ f (x2 )
Sea f (x) =
2x − 5
.
3
1. f es una función lineal, Dom(f ) = R, Rec(f ) = R
2. Intercepciones con el eje X:
2x − 5
y = 0 =⇒
= 0 =⇒ x = 5/2
(5/2, 0)
3
Intercepciones con el eje Y :
x = 0 =⇒ y = −5/3.
(0, −5/3)
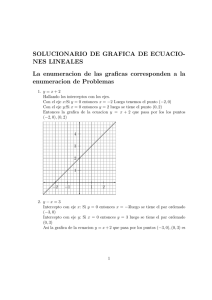
3. La gráfica de y = f (x) es una recta cuya pendiente es
2/3. Luego, es creciente.
Inst. de Matemática y Fı́sica
Universidad de Talca
Gráfica de la función y = f (x)
1
Matemática 1 - CPA
Unidad 3: Función Lineal
Contenidos
Ejemplo 2
Sea f (x) = −2x + 6.
1. Graficar y = f (x)
Solución
Gráfica de la función y = f (x)
• y = 0 =⇒ −2x + 6 = 0 =⇒ x = 3
• x = 0 =⇒ y = 6
• La gráfica de f es la gráfica de y = f (x), o
gráfica de y = −3x + 6 es una recta que pasa
por los puntos (3, 0), (0, 6):
2. Graficar g(x) = −2x + 6, para x ∈ [1, 2[
• Dom(g) = [1, 4[;
• Primero se grafica y = −2x + 6 (grafica
anterior)
• La gráfica de g(x) = −2x + 6, para x ∈
[1, 2[ es un segmento de la recta y = −2x+
6, tal que 1 ≤ x < 2
• ¿Cuál es el recorrido de g?.
3. Graficar h(x) = −2x + 6, para x ∈ [−1, 2]
• Dom(h) = [−1, 4];
• Primero se grafica y = −2x + 6 (grafica
(a))
• La gráfica de h(x) = −2x + 6, para x ∈
[−1, 2] es un segmento de la recta y =
−2x + 6, tal que −1 ≤ x ≤ 2
• ¿Cuál es el recorrido de h?.
Ejemplo 3. Sea y = f (x) una función lineal, tal que f (−1) = 2,
f (−10).
Solución
f (2) = 5. Hallar f (x), y luego hallar
1. Sea f (x) = ax + b. Se debe hallar a y b y una fórmula explı́cita para f (x).
f (−1) = 2 =⇒ −a + b = 2
f (2) = 5 =⇒ 2a + b = 5
Resolviendo el sistema se obtiene: a = 1, b = 3.
Luego f (x) = x + 3.
2. f (−10) = 13
Inst. de Matemática y Fı́sica
Universidad de Talca
2