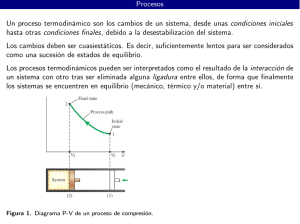
Document
Anuncio

Proceso Estocástico
Un fenómeno estadístico que evoluciona en el tiempo de acuerdo a leyes probabilísticas
se llama proceso estocástico.
La serie de tiempo puede ser vista como una realización, producto de esa ley
probabilística. Al analizar una serie de tiempo la estamos concibiendo como una
realización de un proceso estocástico.
Cada x t es la realización de cierta variable aleatoria X t . Una serie de tiempo x t de T0
datos, {x t , t ∈ T0 }, es una muestra de tamaño uno del vector de T0 variables aleatorias
ordenadas en el tiempo, es decir, es una realización de la familia de variables aleatorias
{X t , t ∈ T0 }.
Algunas definiciones
1. Un proceso estocástico es una familia de variables aleatorias {X t , t ∈ T } definidas
en un espacio de probabilidad {Ω, F, P}, donde T es un subconjunto de R,
generalmente puntos del tiempo {0, ±1, ±2, ...}; {0, 1, 2, 3, ...}; [0; ∞]; (-∞; ∞).
Nota: Para cada t ∈ T , X t es una función en Ω. Por otra parte, para cada ω ∈ Ω ,
X t (ω ) es una función en T .
2. Una realización de un proceso estocástico se define como una función
{X (ω ),ω ∈ Ω} en T, que también se conoce con el nombre de trayectoria del
proceso {X t , t ∈ T }.
Ejemplo 1: Sean A y θ variables aleatorias independientes, A ≥ 0; θ ∈ U [0,2π ]. Un
proceso estocástico {X t , t ∈ T } puede definirse en términos de A y θ para cualquier
v ≥ 0 y r > 0:
1
1
X t = A cos(vt + θ ) , ó, más explícitamente, X t (ω ) = A(ω )cos(vt + θ (ω )) con ω ∈ Ω .
r
r
Las realizaciones de este proceso son las funciones de t que se obtienen al fijar ω , es
decir
1
x (t ) = a cos(vt + θ ) .
r
3. La función de distribución de un proceso estocástico:
{
}
Sea X t , t ∈ T ⊂ R y Γ
Γ = {t = (t1 , t 2 , , t n ) ∈ T n : t1 < t 2 <
< t n ; n = 1,2,
}.
{
}
Las funciones de distribución (de dimensión finita) de X t , t ∈ T son las funciones
{Ft (.), t ∈ Γ} definidas para t = (t1 , t 2 , , t n ) por
(
)
Ft (X ) = P X t1 ≤ x1 , X t2 ≤ x 2 ,...., X tn ≤ x n , X = ( x1 , ..... x n )'∈ R n
.
1
Cada observación es una variable aleatoria y la misma evoluciona en el tiempo de
acuerdo a ciertas leyes probabilísticas.
E (ε t ) = 0 V (ε t ) = σ 2 COV (ε t , ε s ) = 0
;
;
si t ≠ s . Un
{x , , xT }, un grupo diferente de
grupo particular de
produce un conjunto 0
épsilons, produciría otro conjunto distinto de x’s. Hay infinitos conjuntos de
realizaciones posibles en t=1, 2, 3, ...,T.
Ejemplo:
X t = ε t + θε t −1
, con
{ε 0 , , ε T }
{X 0 , X T }.
El modelo define así una distribución conjunta para las variables aleatorias
Los momentos del proceso estocástico se definen con respecto a la distribución de las
X , , XT
variables aleatorias 0
. Pero el problema es que tenemos sólo una observación
para cada momento del tiempo (t), lo que da paso a la idea de estacionariedad.
La importancia del concepto de estacionariedad radica en que, dado que sólo contamos
con una observación para cada momento del tiempo, una única realización, que las
series manifiesten tener propiedades invariantes en el tiempo cobra una importancia
fundamental. En la práctica pocas series presentan esta característica, son no
estacionarias, pero se han diseñado filtros que la transforman en una serie con
comportamiento estable, más adelante veremos qué transformaciones se puede aplicar y
los efectos que inducen. De todos modos hay que considerar que la observación de esta
característica depende del período de observación, esto es, del período que abarca las
observaciones con que contamos, pues una serie puede ser estable durante un período
corto pero no estacionaria en un período mayor. Si consideramos la variable
temperatura de la tierra, esta serie puede ser estacionaria si consideramos un período de
20 años, en cambio, puede mostrar una tendencia creciente si ampliamos
sustancialmente el período de medición.
Hay dos formas equivalentes de enfocar el tema de series de tiempo, desde el dominio
del tiempo y desde el dominio de las frecuencias. El primer enfoque se apoya en una
herramienta fundamental para el análisis, la función de autocovarianzas. El segundo
enfoque se basan en la extensión del análisis de Fourier, que se apoyan en la idea de
que, en un intervalo finito, cualquier función analítica puede ser aproximada, con el
grado de precisión deseado, aproximándola mediante una suma ponderada de funciones
seno y coseno en las frecuencias armónicas. Un proceso Yt puede ser modelizado
mediante una suma ponderada de componentes periódicos a los que se les superimpone
un componente aleatorio.
Función de Autocovarianzas (FACov)
La matriz de covarianzas es un instrumento sumamente útil cuando se trabaja con un
número finito de variables aleatorias, ya que permite visualizar la estructura interna de
un proceso desde una perspectiva temporal, desentrañar las regularidades existentes. En
el caso de una serie de tiempo, {X t , t ∈ T } es necesario extender el concepto de matriz
de covarianzas para trabajar con conjuntos infinitos de variables aleatorias. La Función
de Autocovarianza (FACov) nos proporciona la extensión requerida.
2
Si {X t , t ∈ T } es un proceso tal que la V (X t ) < ∞ para cada t∈T, entonces la FACov
γ X (.,.) de {X t } se define como:
γ X ( r, s ) = Cov( X r , X s ) = E [( X r − E ( X r ))( X s − E ( X s ))], r, s ∈ T
Estacionariedad débil
La serie de tiempo {X t , t ∈ Z }con
débilmente estacionaria si:
2
E [X t ] < ∞ ∀t ∈ Z
Z = {0,±1,±2,
}
es covarianza estacionaria ó
E [X t ] = µ ∀t ∈ Z
γ X ( r , s ) = γ X ( r + t , s + t ) ∀ r , s, t ∈ Z
Observación: Si {Xt,t∈Ζ
Ζ} es estacionaria, entonces γ X (r , s ) = γ X (r − s, 0) ∀ r , s, ∈ Z .
Estacionariedad estricta
Un proceso es estrictamente estacionario si sus propiedades no se ven afectadas por un
cambio en el período de análisis, si la distribución conjunta asociada a un conjunto de m
observaciones x1, x2,......xm es la misma a la asociada a x1+k, x2+k,.........xm+k.
La serie de tiempo {X t , t ∈ Z } se dice estrictamente estacionaria si las distribuciones
conjuntas de ( X t1 ,...., X tk )' y ( X t1 + h ,...., X tk + h )' son las mismas para todo entero
positivo k, y para todo t1 , , t k , k ∈ Z . La distribución conjunta de cualquier conjunto
de variables no se modifica si trasladamos las variables en el tiempo.
Nota: Si {X t } es estrictamente estacionaria, tomando k = 1 en la definición anterior se
puede ver que X t tiene la misma distribución para todo t ∈ Z . Si la E (X t2 ) < ∞
entonces la E (.) y la V (.) son constantes. Si tomamos k = 2, entonces X t + h y X t tienen
la misma distribución conjunta y por tanto la misma covarianza para todo h ∈ Ζ. Por
tanto, un proceso estrictamente estacionario, con momentos de segundo orden finitos, es
estacionario. El recíproco no es cierto en general.
El concepto de estacionariedad permite pasar de agregar observaciones en un momento
a agregarlas a través del tiempo. Ello requerirá la independencia con respecto al tiempo
de los momentos E (.) , V (.) y COV (.) :
E ( X t ) = µ ; E ( X t − µ ) 2 = γ 0 ; E [( X t − µ )( X t +τ − µ )]= γ τ
Si {Xt,t∈Ζ
Ζ} es débilmente estacionaria, entonces γ X (r , s ) = γ X (r − s, 0) ∀ r , s, ∈ Z .
Esta observación permite redefinir la FACov de un proceso estacionario como función
de una sola variable:
γ X (h) ≡ γ X (h, 0) = Cov( X t + h , X t ) ∀ t , h ∈ Z .
La función γ X (.,.) será referida como la FACov de {X t } y γ X (h ) como su valor en el
rezago h.
3
La función de autocorrelación (FAC) del proceso estacionario {X t } es una medida
normalizada de la función de autocovarianza y se define como
ρ X ( h ) ≡ γ X ( h ) / γ X (0) = Corr ( X t + h , X t ) ∀ t , h∈ Z
A diferencia de la función de autocovarianzas la función de autocorrelación es
independiente de la escala de medidade la serie, γh = ρh σ2 .
Propiedades de la FACov
a ) γ (k ) = γ ( −k )
b ) γ ( 0) = V ( X t ) ≥ 0
c ) | γ ( k ) |≤ γ (0)
d ) γ ( k ) es una matriz semidefinida positiva ∴V ( a ' x ) ≥ 0
Ejemplo: Sea X 1 , X 2 , X 3 , tres realizaciones de un proceso estacionario , siendo t= 1, 2, 3.
La matriz de correlaciones entre estas 3 variables será:
Pn =
ρ1
1
ρ1
1
ρ1
ρ
2
ρ2
ρ1
1
y de acuerdo con la propiedad d), esta matriz es semi definida positiva, por lo cual todos
sus menores principales deben ser positivos.
2
a ) Menor principal : 1 − ρ1 ≥ 0 ⇒ ρ1 ≤ 1
2
2
2
2
2
2
b) Determinante : 1 + 2 ρ1 ρ 2 − ρ 2 − 2 ρ1 = 1 − 2 ρ1 (1 − ρ 2 ) − ρ 2 = (1 + ρ 2 )(1 − ρ 2 ) − 2 ρ1 (1 − ρ 2 ) =
[
2
]
(1 − ρ 2 ) 1 + ρ 2 − 2 ρ1 ≥ 0
Esto implica que –1<ρ1<1, –1<ρ2<1 y − 1 <
ρ 2 − ρ12
<1
1 − ρ12
Si los dos factores fueran negativos, llegamos a una contradicción con la primera
2
restricción (ejercicio). Por tanto los dos deben ser positivos, en cuyo caso ρ 2 ≥ 2 ρ 1 − 1
Lo que este ejemplo muestra es que ρ1 y ρ 2 no pueden tomar cualquier valor para estar
en presencia de una FAC.
Ejercicios:
Discutir la estacionariedad
Caso 1.
X t = α cos(θ t ) + β sen(θ t ), t ∈ Z
α y β v.a. no corr.
E (α ) = E ( β ) = 0; V (α ) = V ( β ) = 1; θ fijo.
Note que cos(X ± Y ) = cos(X )cos(Y ) ± sen (X )sen (Y )
Caso 2.
4
Y t = X 1 + X 2 + .... + X t
X t → NI (0, σ 2 );
E (Y t ) = 0
Serie de Tiempo Gaussiana o Normal
El proceso {X t } se dice Gaussiano o Normal si y sólo si las funciones de distribución de
{X t } son todas Normales Multivariadas.
Nota: Si {X t , t ∈ Z } es un proceso Gaussiano y débilemnte estacionario, entonces es
estrictamente estacionario, ya que para todo n ∈ {1,2, } y para todo h, t1 , t 2 ∈ Z los
vectores ( X t1 ,...., X tk )' y ( X t1 + h ,...., X tk + h )' tienen la misma media y matriz de
covarianzas, y por tanto la misma distribución.
Operador de Rezagos
Notaremos L al operador de rezagos. Es un operador lineal, tal que, aplicado a
x t produce x t −1 :
Lxt = xt −1 .
Se extiende fácilmente a más rezagos L j x t = x t − j , j = 0,1,
L puede manipularse como cualquier cantidad algebraica.
Una constante se interpreta como una función que es constante en el tiempo, por tanto
aplicar el operador de rezagos a una constante, no da lugar a modificaciones.
L(a) = a , a = cte.
Es un operador lineal, por tanto si:
L(a Xt + b Yt) = a Xt-1 + b Yt-1
Sea un proceso autorregresivo de orden 1
xt = φ xt −1 + ε t
φ ( L) = (1 − φ L )xt = ε t
∞
∞
j =0
j =0
xt = ∑ φ jε t − j = ∑ (φL ) ε t =
j
1
εt
1 − φL
Se pueden definir polinomios en el operador de rezagos, esto presenta la ventaja de que
se operan de la misma manera que los polinomios algebraicos ordinarios.
Obsérvese que el resultado de la progresión geométrica implica tratar a L como si
tuviera “magnitud” 1, más allá de lo que el término magnitud pueda significar.
Operador de Diferencias
Un caso particular de operador polinómico es el operador diferencias, se define como
∆ = (1 − L ) . Por tanto, ∆x t = (1 − L )x t = x t − x t −1 , y al igual que en el caso del operador
de rezagos, se generaliza fácilmente a cualquier número de diferencias: ∆ j = (1 − L )
j
Note que ∆2 = (1 − L ) = (1 + L2 − 2 L ) , es decir que ∆2 x t = x t + x t − 2 − 2 x t −1
2
5
PROCESOS ESTOCASTICOS ESTACIONARIOS
Ruido Blanco
El proceso estocástico débilmente estacionario más simple que se puede definir, se
denomina RUIDO BLANCO (RB). Un proceso estocástico estacionario se denomina
Ruido Blanco si:
1) E ( X t ) = 0 ∀t ∈ Z
σ 2 si k = 0
2) γ ( k ) =
0 si k ≠ 0
Es un proceso con esperanza cero, varianza constante y donde las variables del proceso
están incorrelacionadas para todos los retardos.
El proceso ruido blanco no es necesariamente estacionario en sentido estricto, sólo se
impone incorrelación, por tanto no necesariamente las variables son independientes. Si
se impone la condición de que las variables del proceso tienen distribución normal, el
proceso será estacionario en sentido estricto. Bajo estas características el proceso se
denomina ruido blanco gaussiano.
Procesos Autorregresivos
El proceso {X t , t ∈ T } se dice autorregresivo de orden p; X t → AR ( p ) ⇔
X t = φ1 X t −1 + φ 2 X t − 2 + ..... + φ ` p X t − p + ε t , donde ε t es un ruido blanco y los φ ’s son
coeficientes fijos.
Utilizando el operador de rezagos definido previamente, podemos re-escribir la
expresión anterior:
(1 − φ1 L − φ 2 L2 − ..... − φ ` p L p ) X t = ε t .
Podemos escribir sintéticamente el polinomio en L:
(1 − φ1 L − φ 2 L2 − ..... − φ` p Lp ) = φ ( L) ⇒ φ ( L) X t = ε t
A partir de un RB genero X t . La introducción de los rezagos de X t es lo que introduce
correlación en el proceso (correlación que el RB no tiene).
Cuando p = 1 tenemos un caso muy simple que se presenta a continuación.
Proceso autorregresivo de orden uno, AR(1)
X t = φX t −1 + ε t
Ejemplo:
t
0
1
2
3
4
5
6
εt
-0,12
0,20
0,06
-0,18
-0,04
0,00
X t (φ = 0,5)
0,16
-0,04
0,18
0,15
-0,105
-0,09
-0,045
6
A partir de t = 1, genero un ruido blanco, a partir de ese ruido, de X 0 y de φ ; genero el
resto de la serie. Con este ejemplo muy simple, vemos que se requiere un punto de
partida, un arranque, X 0 = 0,16 en este caso.
Si consideramos la serie de entrada y la de salida, se aprecia es que ε t tiene un
comportamiento más errático que X t , y ello se debe a la parte φX t −1 que es la que da
inercia.
En el trabajo con series temporales estacionarias, iremos viendo que la “forma“ de los
procesos es lo importante. La “forma” del proceso AR(1) no depende de t, es decir, lo
que vale para t, vale para t - 1, t + 1, etc. Ello nos permite utilizar el procedimiento
recursivo, que resulta muy útil para trabajar la serie:
X t = φX t −1 + ε t = φ (φX t − 2 + ε t −1 ) + ε t = φ 2 X t − 2 + φε t −1 + ε t = ......... =
n −1
φ n X t − n + φ n −1ε t − ( n −1) + φ n − 2 ε t − ( n − 2 ) + ..... + φε t −1 + ε t = φ n X t − n + ∑ φ j ε t − j
j =0
Llegados a este punto, nos preguntamos: Dónde comenzó el proceso? En el momento
0?, En -∞? Veremos a continuación que esta decisión es importante.
Estacionariedad e inicio del proceso
1. El proceso comenzó en t = 0 , con X 0 fijo.
Tenemos que:
n −1
X t = φ n X t −n + ∑φ j ε t − j .
j =0
t −1
Si tomamos n = t, tenemos: X t = φ t X 0 + ∑ φ j ε t − j
j =0
E( X t ) = µt = φ X 0
t
1 − φ 2 t 2
t −1
t −1
t
σ
φ2 ≠1
V ( X t ) = V φ X 0 + ∑ φ j ε t − j = V ∑ φ j ε t − j = 1 − φ 2
j =0
j =0
tσ 2
φ 2 =1
Obsérvese que la media depende de t, al igual que la varianza, cualquiera sea el valor de
φ. No tenemos por tanto un proceso estacionario.
Veamos la Covarianza:
t + k −1
t −1
t −1
E ( X t . X t + k ) = E ∑φ jε t − j ∑φ jε t +k − j = ∑φ kφ 2 j E (ε 2 t − j ) =
j =0
j =0
j =0
t −1
φ kV ( X t ) φ 2 ≠ 1
φ k ∑φ 2 jσ 2 =
φ2 =1
j =0
V ( X t )
La covarianza también depende de t (porque la varianza depende de t) como era de
esperar.
Por tanto, si el proceso comenzó en t = 0, con X 0 fijo (no aleatorio), no tenemos
estacionariedad.
El caso φ =1 tampoco es estacionario, pero es un caso muy especial, conocido como
paseo aleatorio.
7
2. El proceso comienza en t = -∞ (|φ | < 1)
En la medida en que el proceso comenzó en el pasado remoto, (t = -∞) el primer término del
proceso desaparece, con lo cual queda redefinido como:
∞
X t = ∑φ jε t − j
0
E( X t ) = µt = φ t X 0 = 0
∞
∞ j
σ2
2
2j
V ( X t ) = V ∑φ ε t− j = σ ∑φ =
= γ ( 0)
1−φ 2
0
j =0
Cov ( X t . X t + k ) = γ ( k ) = φ k γ (0) (tarea )
Por lo tanto, basta con que |φ | < 1 para que el proceso sea estacionario, cuando éste
comenzó en t = -∞ .
Note que ρ ( k ) = γ ( k ) / γ (0) = φ k
3. El proceso comienza en t = 0, pero con X 0 una variable aleatoria
E( X 0 ) = 0 y V ( X 0 ) =
σ
2
1−φ2
y además, X 0 no está correlacionado con ε 1 , ε 2 ,
etc.
X 0 se piensa como una variable aleatoria que es igual al proceso en estado estacionario.
Además consideramos el caso |φ | < 1.
E ( X t ) = µ t = E (φ t X 0 ) = 0
t −1
t −1
φ 2t
1 − φ 2t 2
σ2
2
V ( X t ) = V φ t X 0 + ∑ φ j ε t − j = V (φ t X 0 )+ V ∑ φ j ε t − j =
σ
+
σ
=
2
1−φ 2
1−φ 2
j =0
j =0
1−φ
la varianza de la suma es la suma de las varianzas porque la COV [X 0 , (ε 1 , ε 2 , )] = 0 .
Calculemos ahora las Covarianzas: COV (X t , X t + k ) .
t −1
X t = φ t X 0 + ∑φ jε t− j
j =0
X t +k = φ t +k X 0 +
t + k −1
∑φ
j =0
j
ε t +k − j
2t
t −1
σ2
σ2
σ2
k
2
2j
2t + k
k
2 1−φ
k
E ( X t X t +k ) = φ
+ φ σ ∑φ = φ
+φ σ
=φ
1−φ 2
1−φ 2
1−φ 2
1−φ 2
j =0
Como puede verse, ninguno de los momentos depende de t, por lo que el proceso es
estacionario1.
El punto de partida es importante, pero como vimos, no es preciso que comience en -∞,
basta con que lo haga en t = 0, con X 0 en la solución estacionaria pero en ambos casos
2t + k
se requiere que φ < 1 .
4. Si φ = 1 y X 0 ≡ 0 . E ( X t ) = µ t = 0; V ( X t ) = tσ 2 ; COV ( X t ; X s ) = min(t , s )σ 2 .
1
No se ha dicho nada de la distribución de las variables, por lo que no sabemos si es estrictamente estacionario.
8
Este caso es, como puede apreciarse, no estacionario, y se conoce como Camino
Aleatorio. El tipo de no estacionariedad que propone este modelo es interesante.
Obsérvese que:
X t = X t −1 + ε t
X t −1 = X t − 2 + ε t −1 ⇒ X t = X t − 2 + ε t −1 + ε t ⇒
t −1
X t = X 0 + ∑ε t− j
j =0
el efecto de cualquier suceso que ocurra en el pasado se queda para siempre. Esta es una
diferencia clave con los procesos estacionarios, donde el impacto del pasado remoto
tiende a desaparecer, en la medida en que φ j se hace más y más pequeño.
El tipo de no estacionariedad que se genera cuando φ > 1 es muy especial, genera
procesos explosivos, en la medida en que lo que sucedió en el pasado se hace cada vez
más importante.
Observaciones
Muchas de las consideraciones serán extensibles al modelo AR(p), con p > 1,
1. Diferencia entre esperanza incondicional y esperanza condicional, E (X t ) y
E (X t X t −1 )
Sea el proceso: X t = φX t −1 + ε t
La esperanza incondicional, E (X t ) = 0
En cambio la esperanza condicional, E (X t X t −1 ) = φ X t −1
donde X t −1 está dado, es un dato y será en general diferente de cero.
2. Diferencia entre varianza incondicional y esperanza condicional
V (X t ) ≠ V (X t X t −1 ) (que queda como tarea).
3.En general supondremos que T representa los números enteros, por lo que
supondremos que el proceso comenzó en -∞.
4. X t está correlacionado con ε t , ε t −1 , ε t −2 ,
futuro).
, (el pasado ) pero no con ε t +1 , ε t + 2 ,
,(el
∞
Ello resulta evidente en la formulación del proceso como X t = ∑ φ j ε t − j .
La COV (X t , ε t − j ) = φ σ para j > 0 , pero COV (X t , ε t + j ) = 0 .
j
j =0
2
5.El proceso AR(1) es estacionario si φ < 1 y ocurre:
iii-
El proceso comienza en t = −∞ .
El proceso comienza en t = 0 en la solución estacionaria
6.Si sabemos que X t ∼ AR (1) es estacionario, entonces
X t = φ X t −1 + ε t
E ( X t ) = E (φX t −1 + ε t ) ⇒ µ = φµ ⇒ µ = 0.
9
Multiplicando por X t a ambos lados de la definición del proceso, y tomamos esperanza
tenemos:
E ( X t X t ) = φE ( X t X t −1 ) + E ( X t ε t )
γ 0 = φγ 1 + σ 2
Multiplicando X t por X t −1 a ambos lados y tomamos esperanza tenemos:
E ( X t −1 X t ) = φE ( X t −1 X t −1 ) + E ( X t −1ε t )
γ1 = φ γ 0 + 0 = φ γ 0
Si ahora multiplicamos X t por X t −k con k > 1, y tomamos esperanza, tendremos:
γ k = φ γ k −1 ⇒
γ 0 = φ γ1 +σ 2
γ1 = φ γ 0
γ k = φ γ k −1
1
−φ
− φ γ 0 σ 2
= ⇒
1 γ 1 0
σ2
γ
=
γ 0 1 1 φ σ 2 0 1 − φ 2
⇒
2
2
γ 1 1 − φ φ 1 0 γ = φ σ
=φγ0
1
1−φ 2
En general, γ k = φ k γ 0 ∴ ρ k = φ k
Este método de cálculo para la función de autocovarianza es válido si el proceso es
estacionario.
La expresión de la función de autocorrelación de un proceso AR(1) es igual a las
potencias del perámetro φ y decrece geométricamente hacia cero. Si el parámetro es
positivo, la dependencia lineal del presente de los valores pasados es siempre
positiva. Si el parámetro es negativo, la dependencia es positiva para los rezagos
pares y negativa para los impares (Ver gráficos incluidos en el punto 9).
Hasta ahora hemos trabajado con X t ∼ AR (1) con media 0. El proceso se generaliza
fácilmente para media ≠ 0. Podemos pensar en X t con E (X t ) = µ ≠ 0 . Definamos
entonces X t* = X t − µ .
Este nuevo proceso es tal que:
X t − µ = φ ( X t −1 − µ ) + ε t , de donde X t = φ X t −1 + µ (1 − φ ) + ε t
Obsérvese que en la definición del proceso aparecerá una constante, pero esa constante
no es la media del proceso, µ , sino que está multiplicada por (1 − φ ).
Existen 2 posibles formas para la función de autocorrelación de un AR(1)
Considere las primeras autocorrelaciones del proceso para diferentes valores del
parámetro φ:
10
k
0
1
2
3
4
5
φ=0,8
1,00
0,80
0,64
0,51
0,41
0,33
φ=-0,8
1,00
- 0,80
0,64
- 0,51
0,41
- 0,33
φ=0,5
1,00
0,50
0,25
0,13
0,06
0,03
rho<0
rho>0
1
1
0
0.5
-1
0
1
3
5
7
9
11
13
15
1
3
5
7
9
11
13
15
Note que, para φ no muy grandes, la caída a 0 es rápida. Por ejemplo, para φ = 0,5 , en
el rezago 4 ó 5 la correlación serial ya es casi 0.
Otra forma de verificar si un proceso AR(1) es estacionario es verificando el signo de la
raíz de la siguiente ecuación (1 − φ L ) = 0 . El proceso es estacionario si la raíz es > 1 en
valor absoluto.
1
(1 − φ L) = 0 ⇒ L =
φ
Esta condición es equivalente a φ < 1 .
Proceso autorregresivo de segundo orden, AR(2)
Muchos de los resultados obtenidos hasta aquí pueden generalizarse a procesos de
mayor orden, pero hay una serie de temas que no aparecen en un proceso AR(1) y que
ahora analizaremos el proceso AR(2).
X t = φ1 X t −1 + φ 2 X t − 2 + ε t , donde ε t es un proceso ruido blanco.
Como vimos nos interesa particularmente establecer las condiciones de estacionariedad
del proceso.
Si φ1 = φ 2 = 0, obviamente el proceso es estacionario, pues Xt = εt
Reescribamos el proceso como una ecuación en diferencias:
(1 − φ1 L − φ 2 L2 ) X t = ε t ó lo que es lo mismo
φ ( L) X t = ε t ⇒ Ecuación en diferencias
11
Es una ecuación en diferencias no homogénea2. La solución se halla sumando a la
solución de la homogénea, una solución particular.
Tomando X t − n = 0; X t − ( n +1) = 0; tendremos una solución particular de la forma
n −1
X t = ∑ψ j ε t − j 3.
j =0
Para encontrar la solución de la ecuación homogénea de (1 − φ1 z − φ 2 z 2 ) X t = 0 es
preciso resolver la ecuación característica: (1 − φ1 z − φ 2 z 2 ) = 0 , sean m1 y m2 las raíces
de (1 − φ1 z − φ 2 z 2 ) = 0 ; c1 y c 2 constantes a determinar de acuerdo a ciertas
condiciones iniciales (por donde pasa X t en 2 momentos).
Al resolver la ecuación característica las posibles soluciones a la ecuación homogénea
son:
1. dos raíces reales y distintas ( m1 ≠ m2 ), 2RR≠: X t = c1 (1 / m1 ) + c 2 (1 / m 2 )
t
t
2. dos raíces reales e iguales ( m1 = m2 = m ): X t = ( c1 + c 2 t )(1 / m )
t
3. dos raíces complejas conjugadas ( m1 ≠ m2 ): X t = c1 (1 / m1 ) + c 2 (1 / m 2 )
t
t
La solución de la ecuación en diferencias no homogénea es la suma de la particular y la
homogénea:
n −1
X t = c1 (1 / m1 ) t + c 2 (1 / m 2 ) t + ∑ψ j ε t − j para los casos 1 y 3 y
j =0
n −1
X t = (c1 + c 2 t )(1 / m ) + ∑ψ j ε t − j en el caso 2.
t
j =0
2
Al igual que el resto de las ecuaciones matemáticas, las ecuaciones en diferencias admiten una solución para la
variable incógnita, Yt. La solución a la ecuación en diferencias será generalmente otra función, no un único valor.
Esta solución nos informará acerca de cómo se forman los valores de Yt a través del tiempo, de la variable tiempo y
del componente aleatorio, εt .
El procedimiento general de ecuaciones en diferencias parte de la descomposición de la solución completa en dos
partes, la solución homogénea y la solución particular. La ecuación homogénea considera únicamente los valores de
Yt y su pasado, y como todo sistema homogéneo admite la solución trivial o bien un conjunto infinito de soluciones a
partir de dos constantes arbitrarias. La solución particular atiende a la parte formada por el término independiente, si
existe y la perturbación aleatoria εt .El procedimiento de resolución comprenderá cuatro etapas: identificar la
ecuación homogénea y encontrar las n soluciones posibles, encontrar la solución particular, formar la solución
completa como suma de la homogénea y la particular y finalmente eliminar las constantes arbitrarias imponiendo
condiciones iniciales.
3
Se obtiene esta expresión, realizando sustituciones recursivas en
por ejemplo
llegar a
X t −1 por ( φ1 X t − 2 + φ 2 X t − 3 + ε t −1 )
X t − n y X t − ( n +1)
y
X t = φ1 X t −1 + φ 2 X t − 2 + ε t , sustituyendo
X t − 2 por ( φ1 X t − 3 + φ 2 X t − 4 + ε t − 2 )
hasta
que se asumieron como 0. Desaparecen así las x’s del lado derecho, quedando una suma
sólo en ε’s rezagados.
12
Pero para que podamos decir que el proceso es estacionario, la solución no deberá
depender de las constantes c1 y c 2 , ya que éstas a su vez dependen de las condiciones
iniciales vinculadas a momentos específicos del pasado. Si ello ocurriera, la idea de
estacionariedad se vería comprometida. Para que el proceso sea estacionario, es preciso
que la solución sea independiente de las condiciones iniciales.
En el caso de 2RR≠, m1 ≠ m2 .
Si al tiempo [ t − n ] y [ t − (n + 1) ] cuento con ciertas condiciones iniciales, es decir,
conozco dos valores del proceso, X t −n y X t −(n +1) , tenemos:
X t −n
1
= c1
m1
X t − n −1
t −n
1
= c1
m
1
1
+ c 2
m2
t − n −1
t −n
1
+ c 2
m2
t − n −1
Inicio del Proceso
Nuevamente es preciso discutir diferentes situaciones:
1. El proceso comenzó en t = 0 .
2. El proceso comenzó en t = −∞ (n = ∞ ).
3. El proceso comenzó en t = 0 , pero con X t −n y X t −n −1 v.a. en la solución
estacionaria.
Veamos el caso 2. Aquí es preciso que m1 y m2 sean ambos mayores que 1 en valor
absoluto, de manera que al ser elevados a la n = ∞ , c1 y c 2 se hagan 0, y de este modo
se independiza la solución de las condiciones “iniciales” X t −n y X t −n −1 .
0
0
∞
∞
j =0
j =0
La solución queda: X t = c1 (1 / m1 ) + c 2 (1 / m 2 ) t + ∑ψ j ε t − j = ∑ψ j ε t − j , y de esta
t
forma X t se independiza del pasado infinito.
Ejercicio: demostrar que si el proceso comenzó en t = 0 el proceso no es estacionario, y
que si comenzó en t = 0 con X t −n y X t −n −1 variables aleatorias en la solución
estacionaria, el proceso es estacionario, exactamente igual que en el caso AR(1).
Representación del proceso como una suma de innovaciones
Determinación de los ψ k
Trabajaremos de ahora en más suponiendo que el proceso comenzó en el pasado
remoto, en t = −∞ . Por lo tanto, el proceso AR(2), como acabamos de demostrar,
puede escribirse como:
∞
∞
k =0
k =0
X t = ∑ψ k ε t −k = ∑ψ k Lk ε t =ψ ( L)ε t
13
Por otra parte, en la definición del proceso escribimos:
1
φ ( L) X t = ε t , de donde X t =
ε t . Igualando los coeficientes de ε t , tenemos:
φ ( L)
1
ε t ⇒ψ ( L)φ ( L) = 1
ψ ( L)ε t =
φ ( L)
(ψ 0 + ψ 1 L + ψ 2 L2 +ψ 3L3 + ...)(1 − φ1 L − φ 2 L2 ) = 1
ψ0 =1
ψ 1 −ψ 0φ1 = 0 ⇒ ψ 1 = φ1
ψ 2 −ψ 1φ1 −ψ 0φ 2 = 0; y en general
ψ k −ψ k −1φ1 −ψ k −2φ 2 = 0 ∀k ≥ 2
(1 − φ L − φ L )ψ
1
2
2
k
=0
Esta es la misma ecuación en diferencias que define al proceso AR(2). Además
conocemos condiciones iniciales: ψ 0 = 1 y ψ 1 = φ1 .
Para qué trabajar con los ψ k ? En ocasiones es más fácil trabajar con el proceso
∞
planteado en la forma X t = ∑ψ k ε t −k , por ejemplo para calcular Esperanzas, Varianzas
k =0
y Covarianzas.
Las soluciones posibles a 1 − φ1 z − φ 2 z 2 = 0 son las mismas que mencionáramos
precedentemente, ya que la ecuación característica es la misma:
a) 2 Raíces Reales distintas:
t
t
ψ t = c1 (1 / m1 ) + c 2 (1 / m2 ) ; ψ 0 = 1, ψ 1 = φ1
ψ 0 = c1 + c 2 = 1
c1 c 2
+
= φ1
m1 m 2
m1 y m2 a su vez son función de φ1 y de φ 2 por lo cual c1 y c 2 también lo serán.
Una vez determinados c1 y c 2 se reemplazan en la fórmula para calcular ψ t
quedando así determinado ψ t para todo t.
b) 2 Raíces Reales iguales:
t
ψ t = (c1 + c 2 t )(1 / m )
ψ 0 = c1 = 1
ψ1 =
c1 + c 2
= φ1
m
Idem al caso anterior, se determinan c1 y c 2 y se reemplazan en la fórmula para
calcular ψ t .
c) 2 Raíces Complejas y Conjugadas:
ψ1 =
Siendo i = − 1 , las raíces de la ecuación característica serán de la forma
14
m = a ± bi = re ± iθ = r (cos(θ ) ± isen(θ ) ) = re ± iθ
r = a ± bi = a 2 + b 2
cos(θ ) =
θ:
sen(θ ) =
a
r
b
r
−π ≤θ ≤ π
Observación:
La igualdad entre la forma trigonométrica y exponencial r (cos(θ ) ± isen(θ ) ) = re ± iθ
Proviene de los siguientes desarrollos de cos θ y i sen θ en el punto θ = 0 :
θ2 θ4 θ6
cosθ = 1 −
+
−
+ .......
2! 4! 6!
3
5
7
iθ
iθ
iθ
isenθ = iθ −
+
−
+ .......
3!
5!
7!
θ 2 iθ 3 θ 4
cosθ + isenθ = 1 + iθ −
−
+
+ ......... = e iθ
2!
3!
4!
A estas representaciones se les denomina forma cartesiana, trigonométrica y
exponencial.
La solución general tiene la misma estructura que se mostró antes:
t
t
1
1
1
ψ t = c1 e − iθt + c 2 e iθt =
r
r
r
t
[(c 2 + c1 )cos (θ t ) + i (c 2 − c1 )sen (θ t )]
c1 y c 2 serán también complejos conjugados:
con c1 + c2 =A y c2 – c1 = B
A = C cos (ε)
B = C sen (ε)
y es equivalente a escribir:
ψ t = C (1 / r ) t [sen (θ × t − ε )]
t
1
domina la tendencia. Si r > 1, tiende a 0 al tender t a ∞. Si r < 1, tiende a ∞ al
r
tender t a ∞.
t
t
1
1
El parámetro define la amplitud de la representación C . Para que la
r
r
secuencia representada por Yt sea convergente, será necesario que r > 1 en valor
absoluto.
15
El parámetro θ representa la frecuencia angular y define el número de ciclos por
unidad de tiempo, la inversa del período. La frecuencia se mide en radianes.
El parámetro ε representa la fase, la situación del ciclo en cada momento del tiempo,
define la ordenada en el origen t = 0.
ψ 0 = c1 + c 2 = 1
1
ψ 1 = [(c 2 + c1 ) cos θ + i (c 2 − c1 )sen θ ] = φ 1
r
Como c1 y c 2 son complejos conjugados, los ψ t son siempre reales.
Aunque esta expresión es algo compleja de obtener, permite establecer con sencillez
los patrones de evolución temporal del proceso, ya que lo que obtuvimos es una
función trigonométrica sencilla de representar, con claros patrones periódicos.
ϕκ − Raíces complejas
ϕκ
1
2
3
4
5
6
7
8
9
10 11
12
13
14 15
16
17 18 19
20
Cuando las raíces son reales, la convergencia a 0 es exponencial. Cuando las raíces son
complejas, la convergencia a 0 es oscilante.
Ejemplo: AR(2)
1- (1 − 0,75L + 0,125L2 )X t = ε t
2- (1 − 0,8 L + 0,6 L2 )X t = ε t
−1
m2
n −t
1
c1
1
1 c1
m1
m1n −t X t −n
+ ∑ψ k ε t −k ; y =
entonces:
X t = t
t
m
−
1
c
X
c
m
m
−
m
m
1
k
=
0
2
t −n −1
2
1
2 2
1
n −t
n −t
m
m
2
2
n −1
m2 m1
− 1 1
1
1
n − n X t −n +
n + n X t −n −1 + ∑ψ k ε t −k
X t =
k =0
m2 − m1 m1 m2
m2 − m1 m1 m2
n −1
En este caso particular, m1 = 2 y m2 = 4 .
n −1
1 4
2
1 −1 1
X t = n − n X t −n + n + n X t −n −1 + ∑ψ k ε t −k
22
4
22
4
k =0
Como las raíces son mayores que 1, a medida que crece n el pasado va perdiendo
importancia, y el proceso depende cada vez menos de condiciones iniciales.
Si hacemos n = 1 :
16
X t = 0,75 X t −1 − 0,125 X t − 2 + ε t
En el segundo ejemplo las raíces serán complejas:
0,8 ± − 1,76 2
1 − 0,8 z + 0,6 z 2 = 0 ⇒ z = a ± bi =
= ± 1,10554 i . Podemos expresar
1,2
3
esto de diferentes formas más o menos convenientes. Una forma que permite visualizar
el comportamiento tanto de la FAC como de los ψ k es hacer que aparezca el módulo
del complejo: r.
r = a 2 + b 2 = 1,291
cosθ = 0,5164 ⇒θ = 0,3273π
a ± bi = r (cosθ ± i sen θ ) = re ± θi = 1,291e ± 0,3273πi
la fórmula que deriváramos para ψ k era:
k
k
1
1
1
ψ k = c1 e − iθ k + c 2 e iθk =
r
r
r
ψk
1
=
1,291
k
[(c 2
k
[(c 2 + c1 )cos (θ k ) + i (c 2 − c1 )sen (θ k )]
+ c 1 )cos (0,3273 π k ) + i (c 2 − c 1 )sen (0,3273 π k )]
calculando c1 y c 2 (tarea) obtenemos:
k
ψk
1
=
[cos (0,3273 π k ) − i 0,603 sen (0,3273 π k )]
1,291
La expresión del segundo paréntesis oscilará acotada, por lo que (como ya sabemos) la
convergencia estará determinada sólo por la expresión en el primer paréntesis.
En este caso,
1
= 0,7746 < 1 , y por tanto los ψj irán a 0 a medida que k crezca. La
1,291
evolución será precisamente la mostrada en el gráfico de ψj presentado anteriormente.
Observación 1: Los ψ k se irán a 0 en forma sinusoidal (raíces complejas) o lo harán
como combinación lineal de términos exponenciales.
Observación 2: Condición de estacionariedad
Para que X t sea una serie estacionaria, necesitamos que los momentos no dependan de
t.
∞
∞
k =0
k =0
X t = ∑ψ k ε t −k ; E ( X t ) = 0; V ( X t ) = σ 2 ∑ψ k2 , ambos momentos son independientes de
t. Además la V (X t ) debe ser finita. Entonces habrá que exigir que
∞
∑ψ
k =0
2
k
<∞.
∞
1
1
< ∞ ⇒ ∑ψ k2 < ∞ y además ψk ≤ c1 k + c 2 k
k =0
k =0
m1
m2
para el caso de 2 raíces reales y distintas, etc.
∞
∞
∞
COV ( X t X t + s ) = E ∑ψ k ε t −k ∑ψ i ε t + s −i = σ 2 {ψ 0ψ s + ψ 1ψ s +1 + ... }= σ 2 ∑ψ kψ k + s = γ s
i =0
k =0
k =0
no depende de t y además es finita.
Se puede demostrar que si
∞
∑ψ
k
17
Estas son las condiciones que deben cumplir la esperanza, varianza y autocovarianzas para que
un proceso sea estacionario.
Observación 3: Condición de estacionariedad sobre φ1 y φ 2
Para que las raíces sean mayores que 1 en módulo,
− φ1 ± φ1 + 4φ 2
2φ 2
> 1 , debe
φ 2 + φ1 < 1
cumplirse que: φ 2 − φ1 < 1
φ <1
2
Y esto se puede graficar:
φ2
2
1
φ2-φ1=1
φ2+φ1=1
0
-3
-2
-1
0
1
2
3
-1
-2
Para que las raíces sean complejas, φ12 + 4φ 2 < 0 . Además las desigualdades son
estrictas, el borde no entra.
Cálculo de los γ k
Los γ k por definición se calculan como la Covarianza entre X t y X t −k . Pero si
φ1 es:
sabemos que el proceso AR(2)Raíces
es estacionario,
Complejasuna forma más simple
X t = φ1 X t −1 + φ 2 X t − 2 + ε t
(i ) E ( X t ) = µ = φ 1 µ + φ 2 µ ⇒ µ = 0
4φ2+φ12=1
Multiplicamos ahora el proceso por X t , y tomamos esperanza a ambos lados de la
igualdad:
E ( X t X t ) = φ1 E (X t −1 X t ) + φ 2 E (X t − 2 X t ) + E (ε t X t )
γ 0 = φ 1γ 1 + φ 2 γ 2 + σ 2
18
multiplicando el proceso por X t −1 y tomando esperanza,
γ 1 = φ1γ 0 + φ 2 γ 1 + 0
multiplicando el proceso por X t −2 y tomando esperanza,
γ 2 = φ 1γ 1 + φ 2 γ 0
y en general,
γ k = φ1γ k −1 + φ 2 γ k − 2 ∀k > 1 , es decir, γ k satisface la misma ecuación en diferencias
que el proceso X t : (1 − φ1 L − φ 2 L2 )γ k = 0 ∀k > 1 . Las que serán diferentes serán las
condiciones iniciales, las cuales obtendremos a partir de γ 0 , γ 1 y γ 2 .
− φ 2 γ 0 σ 2
− φ 1 γ 1 = 0
1 γ 2 0
− φ1
Si dividimos en la definición de la ecuación diferencial por γ 0
1
− φ1
−φ
2
− φ1
1
(1 − φ L − φ L )ρ
tenemos:
= 0 ∀k > 1
A través de los dos ejemplos, tenemos dos modelos para mostrar autocorrelación. Uno
donde los gammas tienden a 0 en forma oscilante, que es el caso de raíces complejas, y
otro donde la evolución hacia cero será una combinación lineal de dos exponenciales.
1
2
2
k
19