INTRODUCCION AL METODO GRAFICO Antes de entrarnos

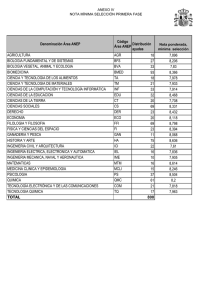
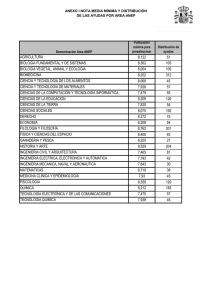
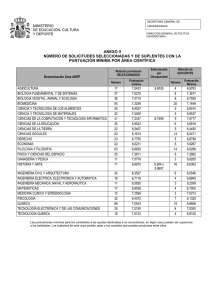
ESCUELA DE CIENCIAS CIENCIAS BASICAS TECNOLOGIA E INGENIERIA
100404-PROGRAMACION LINEAL
Act No. 8. LECTURA LECCION EVALUATIVA 2
INTRODUCCION AL METODO GRAFICO
Antes de entrarnos por completo en los métodos analíticos de la investigación de
operaciones es muy conveniente ver un poco acerca de las desigualdades de una
ecuación lineal.
Por ejemplo tenemos la ecuación
2X + 3Y = 60 en donde X, Y >= 0
Es decir que para que se cumpla la igualdad de la ecuación nos tocaría adquirir 15
unidades de X y 10 unidades de Y respectiva mente:
2(15) + 3(10) = 60
Y la solución se daría por la misma línea recta.
Pero por otra parte si en la ecuación no se quiere llegar a la totalidad del resultado
se dará la ecuación en una forma diferente llamada inecuación:
2X + 3Y <= 60 en donde X, Y >= 0
Dándose como solución factible un área sombreada que depende del signo de la
desigualdad. Si el signo es el <= la solución será el área inferior esa se sombreará
1
ESCUELA DE CIENCIAS CIENCIAS BASICAS TECNOLOGIA E INGENIERIA
100404-PROGRAMACION LINEAL
Act No. 8. LECTURA LECCION EVALUATIVA 2
o si por el contrario el sigo es >= el área a sombrear será la de todos los puntos
por encima de la línea obtenida.
En la anterior grafica la solución más factible es la de los puntos más cerca del eje
X (bajo la recta de la solución lineal ya que la ecuación es precedida por el signo
>=.
DEFINICION Y CONCEPTO GENERAL DE METODO GRAFICO
Ahora se considerara la forma en que se pueden resolver problemas de tipo lineal,
en donde la función dada se tendrá que maximizar o minimizar. Una función lineal
en x y y tiene la forma:
Z = ax + by
Donde a y b son constantes.
También se requerirá que las restricciones correspondientes estén representadas
mediante un sistema de desigualdades lineales o ecuaciones en x y en y y que
todas las variables sean no negativas.
A un problema en el que intervienen todas estas condiciones se le denomina
problema de programación lineal.
La programación lineal fue desarrollada por George B. danzing a fines de la
década de 1940 y se utilizo primero en la fuerza aérea de losa estados unidos
2
ESCUELA DE CIENCIAS CIENCIAS BASICAS TECNOLOGIA E INGENIERIA
100404-PROGRAMACION LINEAL
Act No. 8. LECTURA LECCION EVALUATIVA 2
como auxiliar en la toma de decisiones. En la actualidad tiene amplia aplicación en
el análisis industrial y económico. En un problema de programación lineal a la
función que se desea maximizar o minimizar se le denomina función objetivo.
Aunque por lo general existe una cantidad infinitamente grande de soluciones para
el sistema de restricciones (a las que se denomina soluciones factibles o puntos
factibles), el objetivo consiste en encontrar una de esas soluciones que represente
una solución óptima (es decir una solución que del valor máximo o mínimo de la
fusión objetivo).
En conclusión con lo que acabamos de revisar en la parte anterior sobre las
inecuaciones nos da para definir literalmente el método grafico y el método
algebraico dentro del ámbito de la programación lineal.
Entonces el método grafico en la programación lineal es simplemente sacar de
una situación (problema) ecuaciones lineales y convertirlas en desigualdades o
inecuaciones para poder graficarlas y así sacar la región mas optima dependiendo
del signo de la desigualdad esa área se sombreara y esa será la solución mas
optima del problema.
PASOS PARA LA SOLUCION POR EL METODO GRAFICO
Para llegar a una solución óptima en el método grafico se requiere seguir con una
serie de pasos que podemos dar a continuación:
1. formulación del problema
El primer paso para la resolución por método grafico es expresar el problema en
términos matemáticos en el formato general de la programación lineal
(desigualdades) con un solo fin maximizar la contribución a la ganancia.
2. graficar las restricciones
El próximo paso de la solución por método grafico es la graficación de las
restricciones en el plano cartesiano para establecer todas las posibles soluciones
.3. obtención de la solución optima:
3
ESCUELA DE CIENCIAS CIENCIAS BASICAS TECNOLOGIA E INGENIERIA
100404-PROGRAMACION LINEAL
Act No. 8. LECTURA LECCION EVALUATIVA 2
para encontrar la solución óptima, se grafica la función objetivo en la misma
gráfica de las restricciones. Se graficara siempre la función objetivo del problema y
se dará la solución de acuerdo con el símbolo que este presente en las restricción
de la función objetivo.
EJEMPLO:
Maximizar la función objetivo:
Z= 3x + y
Sujeto a las restricciones:
2x + y <= 8
2x + 3y <= 12
x, y >= 0
A continuación graficamos las desigualdades planteadas en las restricciones así:
2x + y <= 8 x=0; y=8
x=0; x=4
2x + 3y <= 12 x=0; y=4
y=0; x=6
x, y>= 0
4
ESCUELA DE CIENCIAS CIENCIAS BASICAS TECNOLOGIA E INGENIERIA
100404-PROGRAMACION LINEAL
Act No. 8. LECTURA LECCION EVALUATIVA 2
Se observa que la región factible esta conformada por los puntos A(0,0); D(0,4);
B(4,0) y el punto C que es el resultado de la intersección de las 2 inecuaciones
cuyo valor aproximadamente en el plano esta dado por las coordenadas (3,2).
Ahora bien el problema solicita la maximización de Z = 3x + y que se obtiene
precisamente en el punto C(3,2).
METODO ALGEBRAICO
INTRODUCCIÓN
En ocasiones nos encontramos con problemas de índole magnitud, a los cuales se
desea maximizar o minimizar una función sujeta a ciertas restricciones.
Muchas personas califican al método algebraico, como uno de los métodos más
importantes en el campo de la programación lineal. En la actualidad es una
herramienta común, que se ha prestado para resolver problemas de gran
magnitud; por su simplicidad, sencillez y estilo de uso cientos de empresas,
compañías de todo el mundo han ahorrado miles y miles de pesos.
5
ESCUELA DE CIENCIAS CIENCIAS BASICAS TECNOLOGIA E INGENIERIA
100404-PROGRAMACION LINEAL
Act No. 8. LECTURA LECCION EVALUATIVA 2
En este capitulo se tratara la formulación de problemas utilizando el método
algebraico para la solución de problemas de programación lineal. Se hace un
enfoque a la variedad de aplicaciones del método para que el estudiante
interesado pueda tener una visión y ejercitar sus conocimientos.
El método algebraico contempla en su desarrollo al método grafico y de la misma
manera el método grafico no estaría completo sin la rigurosidad del método
algebraico pues la apreciación visual que da el grafico en la solución óptima puede
estar sujeta a error por parte del analista.
PASOS PARA UTILIZAR EL METODO ALGEBRAICO
Dado que tenemos un problema de dos variables, podemos graficar las soluciones
posibles y comprender algunos puntos interesantes respecto a las relaciones
lineales. Veremos la siguiente manera de obtener gráficamente las soluciones al
problema planteado y luego veremos como obtenerlas algebraicamente.
1. Exprésense los datos del problema como una función objetivo y restricciones.
2. Graficar las restricciones.
3. Definir el conjunto factible.
4. Encontrar la solución óptima
EJEMPLOS DESARROLLADOS
A continuación se presentan el análisis algebraico y grafico de algunos problemas
de programación lineal:
PROBLEMA 1:
Supóngase una compañía fabrica 2 tipos de artefactos, manuales y eléctricos.
Cada uno de ellos requiere en su fabricación el uso de 3 maquinas: A, B y C. un
artefacto manual requiere del empleo de la maquina A durante 2 horas, de una 1
en B y una 1 en C, un artefacto eléctrico requiere de 1 hora en A, 2 horas en B y 1
hora en C. supóngase además que el numero máximo de horas disponible por
6
ESCUELA DE CIENCIAS CIENCIAS BASICAS TECNOLOGIA E INGENIERIA
100404-PROGRAMACION LINEAL
Act No. 8. LECTURA LECCION EVALUATIVA 2
mes para el uso de las tres maquinas es 180, 160 y 100, respectivamente. La
utilidad que se obtiene con los artefactos manuales es de 4000 pesos y de 6000
pesos para los eléctricos. Si la compañía vende todos los artefactos que fábrica,
¿Cuántos de ellos de cada tipo se deben elaborar con el objeto de maximizar la
utilidad mensual?
A
B
C
UTILIDAD
MANUALES(X)
2
1
1
4000
ELECTRICOS(Y)
1
2
1
6000
HORAS DISPONIBLES
180
160
100
SOLUCIÓN:
1.Paso: Planteamos la función objetivo y las restricciones correspondientes:
MAX Z= 4000X + 6000Y
SUJETO A:
2X + Y <= 180
X + 2Y <= 160
X + Y <= 100
2.Paso: Elaboramos el gráfico correspondiente a las restricciones con el fin de
precisar la región factible y determinar los puntos que la conforman:
2X + Y <= 180
X=0 Y= 180
Y=0
X + 2Y <= 160
X + Y <= 100
X= 90
X=0 Y=80
Y=0
X=160
X=0
Y=100
Y=0
X=100
7
ESCUELA DE CIENCIAS CIENCIAS BASICAS TECNOLOGIA E INGENIERIA
100404-PROGRAMACION LINEAL
Act No. 8. LECTURA LECCION EVALUATIVA 2
3. Paso: Resolvemos el sistema de ecuaciones para determinar las coordenadas
del punto B y C así:
Para B: X + 2Y <= 160
Para C: 2X + Y <= 180
X + Y <= 100
Y= 60
X = 80
X= 40
Y = 20
4.Paso: Con los puntos de la región factible:
O(0,0) ; B(40,60) ; C(80,20) ; A(0,80); D(90,0) Maximizamos la función objetivo :
MAX Z = 4000x + 6000 y
(0,0) 4000(0) + 6000(0) = 0
(0,80) 4000(0) + 6000(80) = 480000
(40,60) 4000(40) + 6000(60)= 520000
(90,0) 4000(90) + 6000(0) = 360000
5. Paso: La solución para el problema está representada por la fabricación de 40
artefactos manuales y 60 artefactos eléctricos generando una máxima utilidad de $
520.000
METODO SIMPLEX
8
ESCUELA DE CIENCIAS CIENCIAS BASICAS TECNOLOGIA E INGENIERIA
100404-PROGRAMACION LINEAL
Act No. 8. LECTURA LECCION EVALUATIVA 2
En las lecciones anteriores vimos como resolver problemas de programación lineal
a través del método grafico y el método algebraico, surgen grandes limitaciones a
la hora de trabajar con estos dos métodos, es decir que no es posible darle óptima
solución a un problema. Esto se debe a que el método grafico no resulta práctico
cuando el número de variables se aumenta a tres, y con más variables resulta
imposible de utilizar. Por otra parte el método algebraico tarda demasiado tiempo
aun para problemas de pocas variables y restricciones.
El mejor método para resolver un problema de programación lineal es el método
simplex, ya que es un método de fácil aplicación, de tipo algorítmico y conduce a
una eficiente solución del problema.
PASOS PARA EL DESARROLLO DEL METODO SIMPLEX
Elaborar la tabla simplex inicial.
Existen cuatro variables de holgura, S1, S2, S3, y S4; una para cada restricción.
1. Si todos lo indicadores del último renglón son no negativos, entonces Z tiene un
máximo cuando X1=0, X2=0 y X3=0. El valor máximo es 0. Si existen indicadores
negativos, localizar la columna en la que aparezca el indicador más negativo. Esta
columna señala la variable entrante.
2. Dividir cada uno de los elementos de la columna de b que se encuentran por
encima de la recta punteada entre el correspondiente elemento de la columna de
9
ESCUELA DE CIENCIAS CIENCIAS BASICAS TECNOLOGIA E INGENIERIA
100404-PROGRAMACION LINEAL
Act No. 8. LECTURA LECCION EVALUATIVA 2
la variable entrante. Se debe realizar esta división solo en los casos en los que el
elemento de la variable que entra sea positivo.
3. Encerrar en un círculo el elemento de la columna de la variable entrante que
corresponde al menor cociente del paso 3. Este es un elemento pivote. La variable
saliente es la que se encuentra al lado izquierdo del renglón del elemento pivote.
4. Utilizar operaciones elementales sobre renglones para transformar la tabla en
otra tabla equivalente que tenga un 1 en donde se encuentra el elemento pivote y
0 en las demás posiciones de esa columna.
5. La variable entrante debe reemplazar a la variable saliente en el lado izquierdo
de esta nueva tabla.
6. Si todos los indicadores de la tabla nueva son no negativos, ya se tiene una
solución óptima. El valor máximo de Z es el elemento del último renglón y la última
columna. Ocurre esto cuando las variables se encuentran del lado izquierdo de la
tabla son iguales a lo elementos correspondiente de la última columna. Todas las
demás variables son ceros. Si cuando menos uno de los indicadores es negativo,
se debe repetir el mismo proceso con la nueva tabla, comenzando con el paso 2.
EJEMPLOS DESARROLLADOS
EJEMPLO 1
Maximizar Z= 5X1+4X2
Sujeto a: X1+X2 <= 20
2X1+X2 <= 35
-3X1+X2 <= 12
X1>=0, X2>=0
Este problema de programación lineal se ajusta a la forma normal. La tabla
simplex inicial es:
10
ESCUELA DE CIENCIAS CIENCIAS BASICAS TECNOLOGIA E INGENIERIA
100404-PROGRAMACION LINEAL
Act No. 8. LECTURA LECCION EVALUATIVA 2
El indicador mas negativo, -5, aparece en la columna x1. Por ello, x1 es la variable
entrante. El menor cociente es 17.5, de modo que, S2 es la variable saliente. El
elemento pivote es 2. Utilizando operaciones elementales sobre los renglones
para obtener un 1 en la posición del pivote y 0 en las demás posiciones de esa
columna, se tienen:
La nueva tabla es:
11
ESCUELA DE CIENCIAS CIENCIAS BASICAS TECNOLOGIA E INGENIERIA
100404-PROGRAMACION LINEAL
Act No. 8. LECTURA LECCION EVALUATIVA 2
Obsérvese que en el lado izquierdo, x1 reemplazó a S2. Ya que -3/2 es el
indicador más negativo se debe continuar con el proceso. La variable entrante es
ahora x2. El menor cociente es 5. De modo que S1 es la variable saliente y ½ es
el elemento pivote. Utilizando operaciones elementales sobre renglones, se tiene:
Usted podrá encontrar mas ejemplos desarrollados en el modulo.
12