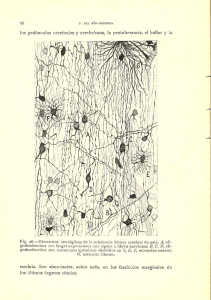
Tenacidad de los compuestos
Anuncio

MATERIALES COMPUESTOS Capítulo 9: Tenacidad de los compuestos • Mecanismos de fractura – – • • Contribuciones al trabajo de fractura en compuestos de matriz frágil Contribuciones al trabajo de fractura en compuestos de matriz ductil – – – – – • Conceptos básicos Despegue de la intercara y deflexión de grietas Deformación de la matriz Rotura de las fibras Despegue de la intercara Deslizamiento y extracción de fibras Efecto de la microestructura Crecimiento sub-crítico de grietas – – Fatiga Corrosión bajo tensión MATERIALES COMPUESTOS Mecanismos de fractura: conceptos básicos • • • • • • Concentración de tensiones (Inglis, 1913) Criterio energético de Griffith (1920) Velocidad de liberación de energía (Irwin, 1948) Factor de intensidad de tensión (Irwin, 1950) Para los metales tenaces, KIc, puede llegar a ser 100 MPa·m1/2 Para los materiales frágiles, KIc, puede llegar a ser 1 MPa·m1/2 MATERIALES COMPUESTOS Despegue de la intercara y deflexión de grietas • • • • • • Un compuesto de matriz y fibras frágiles (vg. epoxi/fibra de vidrio), puede llegar a tener una energía de rotura comparable con la de metales (50 kJ/m2), cuando sus constituyentes no llegan a tener más de 0’01-0’1 kJ/m2 La clave de este comportamiento está en la deflexión de las grietas en la intercara, dando lugar a un comportamiento pseudo-tenaz Se han desarrollado dos tipos de criterios para determinar si la grieta deflectará o no en la intercara: los análisis de tensiones y los energéticos Analisis de tensiones: vg. Cook y Gordon (1964-) Análisis de energías: Kendall (1975); He y Hutchinson (1989) y Gupta (1993) Ejemplo: He y Hutchinson: Gic hm Em + h f E f ≤ G fc hf E f 1 2 4 π(1 − ν ) MATERIALES COMPUESTOS Trabajo de fractura en compuestos de matriz frágil Objetivos • Cuantificar el efecto de los mecanismos disipativos en la absorción de energía de los CMCs • Identificar y cuantificar las causas de la variabilidad del material • Explorar caminos para mejorar las prestaciones de los CMCs MATERIALES COMPUESTOS Comportamiento típico 300 STRESS (MPa) 250 200 150 Dissipated Energy 100 Elastic energy released after fracture 50 0 0 εp 0.2 0.4 0.6 0.8 1 STRAIN (%) CAS/SiC [(0/90)3]s MATERIALES COMPUESTOS Mecanismos disipativos • Durante la fractura: – Rotura de las fibras – Extracción de las fibras • Antes de la fractura: – Agrietamiento de capas a 0 y 90º – Despegue de intercaras – Apertura de grietas MATERIALES COMPUESTOS Energía disipada durante la fractura • Rotura de fibras: – Despreciable • Extracción de fibras: W f = W1 f ⋅ N f = π ⋅ r ⋅ τ s ⋅ l ⋅ 2 f Vf π ⋅ r2 = τ s ⋅ l 2f ⋅ V f r – Para el CAS/SiC estudiado, la mitad de la energía elástica acumulada lc = Wf U el = τ s ⋅ l 2f ⋅ V f r ⋅ U el MATERIALES COMPUESTOS Comportamiento tras la fractura 300 STRESS (MPa) 250 200 150 Elastic unloading (EfVf) 100 Fibre extraction 50 0 0 0.2 0.4 0.6 STRAIN (%) 0.8 1 CAS/SiC [(0/90)3]s MATERIALES COMPUESTOS MEAN PULLOUT LENGTH (µm) Relación energía absorbida / longitud de fibra extraída 500 450 y = -93.177x + 519.34 R2 = 0.1569 400 350 300 250 200 150 100 50 0 0 0.5 1 1.5 2 3 STRAIN ENERGY DENSITY (MJ/m ) 2.5 CAS/SiC [(0/90)3]s MATERIALES COMPUESTOS Relación energía absorbida / densidad de grietas CRACK DENSITY (mm-1) 14 12 10 8 y = 2.1757x + 1.2172 R2 = 0.7851 6 4 2 0 0 1 2 3 4 3 STRAIN ENERGY DENSITY (MJ/m ) 5 CAS/SiC [(0/90)3]s MATERIALES COMPUESTOS Energía disipada antes de la fractura • Agrietamiento de capas a 0º: U cr0 º = ( 0.5 − V f ) ⋅ Vcr ⋅ Γm • Agrietamiento de capas a 90º: 0.5 ⋅ Vcr ⋅ Γi < U cr90 º < 0.5 ⋅ Vcr ⋅ Γm • Despegue de la intercara: 2 U deb = V f ⋅ Vcr ⋅ ld ⋅ ⋅ Γi r • Apertura de grietas: – Despreciable MATERIALES COMPUESTOS Longitud de intercara despegada desde la grieta Crack σf = F= σc Vf Matrix σc − εc ⋅ E f ⋅ π ⋅ r 2 = 2 ⋅ π ⋅ r ⋅ τ s ⋅ ld Vf σc Vf σ f = E f ⋅ εc Fibre ⋅π ⋅ r2 σm = 0 σ m = E m ⋅ εc ld Vm ⋅ π ⋅ r 2 ( εc ⋅ E m ) = 2 ⋅ π ⋅ r ⋅ τ s ⋅ l d Vf Vm ⋅ E m σc ⋅ r ⋅ ld = 2 ⋅ V f ⋅ τ s Vm ⋅ E m + V f ⋅ E f MATERIALES COMPUESTOS Balance global de energía para el CAS/SiC [(0/90)3]s 0.444 MJ/m3 Resto Fractura 0.456 MJ/m3 Anterior a fractura Energía total: 1.43 MJ/m3 0.530 MJ/m3 - Agrietamiento 0º: 13 % - Agrietamiento 90º: 12 % - Despegue 75 % MATERIALES COMPUESTOS Variabilidad global Mean + St. Dev Parameter Influence Lower Upper bound bound Reference 0.48 0.57 Direct 0.51 0.63 τs Direct 0.63 0.72 2Γi Vf Direct 0.53 0.63 r Inverse 0.42 0.50 MATERIALES COMPUESTOS Predicciones del modelo CUMULATIVE PROBABILITY 1 0.9 0.8 0.7 0.6 95% confidence interval for experimental values model prediction 0.5 0.4 0.3 0.2 experimental values 0.1 0 0 0.2 0.4 0.6 0.8 1 1.2 1.4 3 DISSIPATED ENERGY (MJ/m ) CAS/SiC [(0/90)3]s MATERIALES COMPUESTOS Influencia de los parámetros geométricos en el comportamiento global • Radio de las fibras: – Disminuyendo r ⇒ aumenta la energía disipada (α1/r) – Problemas tecnológicos • Fracción volumétrica de fibras: – Aumentando Vf ⇒ aumenta la energía disipada (lineal) – Limitado a 0.30 - 0.35 en cada dirección MATERIALES COMPUESTOS Influencia del radio en la energía absorbida 4 Utot (MJ/m3) 3 2 1 0 0 5 10 15 r (µm) 20 25 CAS/SiC [(0/90)3]s MATERIALES COMPUESTOS Influencia de los parámetros de la intercara en el comportamiento global • Energía de despegue: – Aumentando Γi ⇒ aumenta la energía disipada (lineal) – Límite: el comportamiento pseudo-tenaz • Tensión de deslizamiento: – Aumentando τs ⇒ aumenta la energía disipada (lineal) – Muy poca pendiente (aumentando 100% τs ⇒ aumenta el 30% la energía) MATERIALES COMPUESTOS Conclusiones • La mayoría de la energía disipada en el ensayo se invierte en despegar la intercara • La extracción de fibras contribuye al total de energía disipada solamente si la longitud de la probeta es inferior a lc • La dispersión de los valores de la energía de despegue es el principal responsable de la variabilidad • El camino más prometedor para mejorar las prestaciones de los CMCs parece ser la disminución en el radio de las fibras MATERIALES COMPUESTOS Trabajo de fractura en compuestos de matriz ductil Deformación de la matriz • • • • La mayoría de las matrices metálicas poseen una alta tenacidad; sin embargo, las matrices poliméricas (especialmente las termoestables) y las cerámicas son frágiles La deformación de la matriz puede diferir notablemente de la del mismo material sin reforzar - La causa principal es la constricción, que impide su deformación libre - Otra causa: aparición de estados de tensión triaxial, que inhiben el flujo plástico Consecuencia: se pierde energía de fractura con respecto a la del material sin reforzar. Sólo en metales poco tenaces (cinc) reforzados con fibra larga se gana tenacidad Solución: se está trabajando en mejorar los procesos productivos para obtener una distribución más homogénea del refuerzo, eliminar porosidad y evitar la aparición de intercaras despegadas MATERIALES COMPUESTOS Rotura de fibras • • • La rotura del material generalmente conlleva la de las fibras En la mayoría de los casos, la aportación al global de energía absorbida debida a la rotura de las fibras es despreciable frente a las demás Sólo en casos de fibras no frágiles (kevlar, celulos o metálicas) la aportación es significativa Despegue de la intercara • • En compuestos de matriz dúctil, es frecuente tener refuerzos de fibra corta, que se despegan en el momento de la fractura En estos casos, la energía que se absorbe se puede cuantificar como: G d = V f ⋅ s ⋅ Gid MATERIALES COMPUESTOS Deslizamiento y extracción de las fibras • La extracción de fibras puede suponer un aporte relativamente importante al trabajo de fractura, aún en los compuestos de matriz dúctil. Para fibras de refuerzo cortas, puede estimarse como: Gp = V f ⋅ s2 ⋅ r ⋅ τ i 3 donde s es la relación entre la longitud de la fibra extraida y su radio. El problema es estimar la longitud media de las fibras extraidas Efecto de la microestructura • El comportamiento de un compuesto se puede optimizar desde un punto de • vista de energía de fractura a base de variar características de su estructura, como pueden ser la orientación de las fibras, su longitud, la arquitectura, etc. En general, como ocurre con la carga de rotura, se pueden obtener buenos resultados en una dirección a costa de debilitar otras, o bien materiales casi isótropos planos, pero con características no tan brillantes en una dirección MATERIALES COMPUESTOS Crecimiento subcrítico de grietas Fatiga • • • • La presencia de particulas influye relativamente poco, pero no así la de fibras largas. Esto es especialmente cierto para los compuestos poliméricos La presencia de las fibras modifica la distribución de tensiones en la punta de la grieta: el puenteo de las grietas por parte de las fibras reduce la intensidad de tensión. Además, se producen múltiples grietas, a diferencia de la grieta dominante de las cerámicas monolíticas Los compuestos reforzados por fibras rígidas (vg: carbono), presentan un magnífico comportamiento a fatiga. Fibras poco rígidas (vg: vidrio) no producen apreciables mejoras en el comportamiento a fatiga Los compuestos unidireccionales presentan unas características especialmente brillantes a fatiga, aplicando la carga en la dirección de las fibras. El comportamiento de los refuerzos tejidos o laminados es menos espectacular. Los refuerzos al azar (tipo estera) presentan un comportamiento más bien pobre MATERIALES COMPUESTOS Corrosión bajo tensión • • • • El efecto depende en gran manera de los materiales que forman el compuesto En general, tienen un efecto beneficioso las fibras largas, cuando se disponen en la dirección de la carga. Las fibras no alineadas no mejoran el comportamiento de la matriz sin reforzar Debe tenerse en cuenta no sólo la resistencia a la corrosión de la matriz y las fibras, sino también la de la intercara Es especialmente importante tener en cuenta este efecto en PMC expuestos a ambientes químicamente agresivos